Математические методы планирования экспериментов
1 Общие сведения о планировании эксперимента
2 Краткая характеристика методики составления планов эксперимента для моделей первого и второго порядков
2.1 Общие положения о планировании второго порядка
2.2 Ортогональные центральные композиционные планы второго порядка
2.3 Рототабельные планы второго порядка
ЗАКЛЮЧЕНИЕ
Список использованных источников
ВВЕДЕНИЕ
Развитие современной науки и техники связано с созданием новых и постоянным совершенствованием существующих научных и технологических процессов. Основой их разработки и оптимизации является эксперимент. Заметное повышение эффективности экспериментальных исследований и инженерных разработок достигается использованием математических методов планирования экспериментов. В процессе экспериментирования и при обработке полученных данных существенно сокращает сроки решения, снижает затраты на исследования и повышает качество полученных результатов.
Цель планирования эксперимента – нахождение таких условий и правил проведения опытов при которых удается получить надежную и достоверную информацию об объекте с наименьшей затратой труда, а также представить эту информацию в компактной и удобной форме с количественной оценкой точности.
1. Общие сведения о планировании эксперимента
Инициатором применения планирования эксперимента является Рональд А. Фишер, другой автор известных первых работ – Френк Йетс. Далее идеи планирования эксперимента формировались в трудах Дж. Бокса, Дж. Кифера. В нашей стране - в трудах Г.К. Круга, Е.В. Маркова и др.
Часто, приступая к изучению какого-либо процесса экспериментатор не имеет исчерпывающих сведений о механизме процесса. Можно только указать параметры определяющие условия протекания процесса, и, возможно требования к его результатам. Поставленная проблема является задачей кибернетики. Действительно, если считать кибернетику «наукой, изучающей системы любой природы, способные воспринимать, хранить и перерабатывать информацию для целей оптимального управления» (3), то такую систему можно представить в виде черного ящика.
Черный ящик – объект исследования, имеющий (k + p) входов и m выходов.

Зависимость между выходными параметрами (откликом) и входными параметрами (факторами) называется функцией отклика. Математическая запись функции отклика представлена в виде формулы (1):
![]() (1)
(1)
Этому уравнению в многомерном пространстве соответствует гиперповерхность, которая называется поверхностью отклика, а само пространство – факторным пространством.
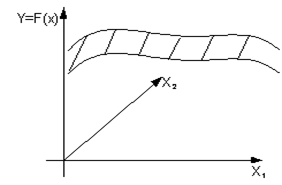
Рисунок 2 – Поверхность отклика
Для математического описания поверхности отдыха используют уравнение:
![]() (2)
(2)
где ![]() - перемешнные факторы при i=1,…,k; u=1,…,k; i
- перемешнные факторы при i=1,…,k; u=1,…,k; i![]() u;
u;
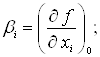
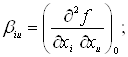
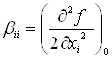 .
.
Это уравнение является разложением в ряд Тейлора неизвестной функции отклика в окрестности точки с ![]() .
.
На практике по результатам эксперимента производится обработка дан\ных по методу наименьших квадратов. Этот метод позволяет найти оценку b коэффициентов ![]() , и данный полином заменяется уравнением вида:
, и данный полином заменяется уравнением вида:
![]() (3)
(3)
которое является регрессионной моделью (моделью регрессионного анализа). В этом выражении ![]() означает модельное, т.е. рассчитываемое по уравнению модели, значение выхода. Коэффициенты регрессии определяются экспериментально и служат для статистической оценки теоретических коэффициентов, т.е.
означает модельное, т.е. рассчитываемое по уравнению модели, значение выхода. Коэффициенты регрессии определяются экспериментально и служат для статистической оценки теоретических коэффициентов, т.е.
![]() (4)
(4)
В регрессионной модели члены второй степени ![]() ,
, ![]()
![]() характеризуют кривизну поверхности отклика. Чем больше кривизна этой поверхности, тем больше в модели регрессии членов высшей степени. На практике чаще всего стремятся ограничиться линейной моделью (1).
характеризуют кривизну поверхности отклика. Чем больше кривизна этой поверхности, тем больше в модели регрессии членов высшей степени. На практике чаще всего стремятся ограничиться линейной моделью (1).
Эксперимент можно проводить по-разному. В случае, когда исследователь наблюдает за каким-то неуправляемым процессом, не вмешиваясь в него, или выбирает экспериментальные точки интуитивно, на основании каких-то привходящих обстоятельств, эксперимент считают пассивным. В настоящее время пассивный эксперимент считается неэффективным.
Гораздо более продуктивно проводится эксперимент, когда исследователь применяет статистические методы на всех этапах исследования, и, прежде всего, перед постановкой опытов, разрабатывая схему эксперимента, а также в процессе экспериментирования, при обработке результатов и после эксперимента, принимая решение о дальнейших действиях. Такой эксперимент считают активным, и он предполагает планирование эксперимента.
Под планированием эксперимента понимают процедуру выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью.
Под математической моделью планирования понимается наука о способах составления экономических экспериментальных данных планов, которые позволяют извлекать наибольшее количество информации об объекте исследования, о способах проведения эксперимента, о способах обработки данных и их использование для оптимизации производственных процессов, а также инженерных расчетов (3).
2. Краткая характеристика методики составления планов эксперимента для моделей первого и второго порядков
Использование теории планирования эксперимента является одним из путей существенного повышения эффективности многофакторных экспериментальных исследований. В планировании экспериментов применяются в основном планы первого и второго порядков. Планы более высоких порядков используются в инженерной практике редко. В связи с этим далее приводится краткое изложение методики составления планов эксперимента для моделей первого и второго порядков. Под планом первого порядка понимают такие планы, которые позволяют провести эксперимент для отыскания уравнения регрессии, содержащего только первые степени факторов и их произведения:
 (5)
(5)
Планы второго порядка позволяют провести эксперимент для отыскания уравнения регрессии, содержащего и вторые степени факторов:
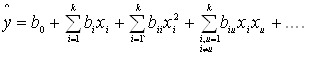 (6)
(6)
Нахождение уравнения регрессии методом планирования экспериментов состоит из следующих этапов:
· выбор основных факторов и их уравнений;
· планирование и проведение собственного эксперимента;
· определение коэффициентов уравнения регрессии;
· статистический анализ результатов эксперимента (1).
2.1 Общие положения о планировании второго порядка
Описание поверхности отклика полиномами первого порядка часто оказывается недостаточным. Во многих случаях удовлетворительная аппроксимация может быть достигнута, если воспользоваться полиномом второго порядка (6).
В этом случае требуется, чтобы каждый фактор варьировался не менее чем на трех уровнях. В этом случае полный факторный эксперимент содержит слишком большое количество опытов, равное ![]() . Так, при
. Так, при ![]() их 27, а число коэффициентов
их 27, а число коэффициентов ![]() , при
, при ![]() число опытов 243, а коэффициентов 21. В связи с этим осуществление полного факторного эксперимента (ПФЭ) для планов второго порядка не только сложно, но и нецелесообразно.
число опытов 243, а коэффициентов 21. В связи с этим осуществление полного факторного эксперимента (ПФЭ) для планов второго порядка не только сложно, но и нецелесообразно.
Сократить число опытов можно, воспользовавшись так называемым композиционным или последовательным планом, разработанным Боксом и Уилсоном. Так, при двух факторах модель функции отклика ![]() второго порядка представляет собой поверхность в виде цилиндра, конуса, эллипса и т.д., описываемую в общем виде уравнением:
второго порядка представляет собой поверхность в виде цилиндра, конуса, эллипса и т.д., описываемую в общем виде уравнением:
![]() . (7)
. (7)
Для определений такой поверхности необходимо располагать координатами не менее трех ее точек, т.е. факторы ![]() и
и ![]() должны варьироваться не менее чем на трех уровнях. Поэтому план эксперимента в плоскости факторов
должны варьироваться не менее чем на трех уровнях. Поэтому план эксперимента в плоскости факторов ![]() и
и ![]() на рисунке 3, а не может состоять лишь из опытов 1, 2, 3, 4, располагающихся в вершинах квадрата, как это делается для модели первого порядка. К ним должны быть добавлены опыты (звездные точки) 5, 6, 7, 8, расположенные на осях
на рисунке 3, а не может состоять лишь из опытов 1, 2, 3, 4, располагающихся в вершинах квадрата, как это делается для модели первого порядка. К ним должны быть добавлены опыты (звездные точки) 5, 6, 7, 8, расположенные на осях ![]() и
и ![]() с координатами
с координатами ![]() и обязательно опыт 9 в центре квадрата, чтобы по любому направлению (5-9-6), (1-9-4) и т.д. располагалось три точки, определяющие кривизну поверхности в этом направлении.
и обязательно опыт 9 в центре квадрата, чтобы по любому направлению (5-9-6), (1-9-4) и т.д. располагалось три точки, определяющие кривизну поверхности в этом направлении.
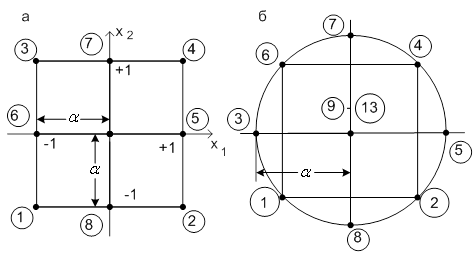
Рисунок 3 – Планы второго порядка при ![]() : а – ортогональный;
: а – ортогональный;
б – рототабельный
Таким образом, в общем случае ядро композиционного плана составляет при ![]() ПФЭ
ПФЭ ![]() , а при
, а при ![]() - дробную реплику от него. Если линейное уравнение регрессии оказалось неадекватным, необходимо:
- дробную реплику от него. Если линейное уравнение регрессии оказалось неадекватным, необходимо:
1) добавить (2 – k) звездных точек, расположенных на координатных осях факторного пространства ![]()
![]()
![]() где
где ![]() - звездное плечо, или расстояние до звездной точки;
- звездное плечо, или расстояние до звездной точки;
2) провести ![]() опытов при значениях факторов в центре плана.
опытов при значениях факторов в центре плана.
При k факторах общее число опытов в матрице композиционного плана составит:
 (8)
(8)
При этом величина звездного плеча ![]() и число опытов в центре плана
и число опытов в центре плана ![]() зависит от выбранного вида композиционного плана.
зависит от выбранного вида композиционного плана.
Композиционный план для ![]() и
и ![]() представлен в таблице 1.
представлен в таблице 1.
Таблица 1 – Композиционный план второго порядка
| Номер опыта | Факторы | Результат | ||||||
|
|
|
|
|
|
| ||
Ядро плана | 1 2 3 4 5 | +1 +1 +1 +1 +1 | - 1 +1 - 1 +1
| - 1 - 1 +1 +1 0 | +1 - 1 - 1 +1 0 | +1 +1 +1 +1
| +1 +1 +1 +1 0 |
|
| Звездные точки | 6 7 8 | +1 +1 +1 |
0 0 | 0
| 0 0 0 |
0 0 | 0
|
|
| Центр плана | 9 | +1 | 0 | 0 | 0 | 0 | 0 |
|
Подобные работы:
Побудова економіко-математичної моделі розробки асортименту швейних виробів
Анализ современного состояния и перспектив развития отрасли связи в Беларуси
Анализ ценовой политики ОАО "Сибирское молоко"
Анализ экономической деятельности станции технического обслуживания автомобилей "Пятое колесо"
Аналіз банківської діяльності на прикладі ПАТ КБ "ПриватБанк"