Теорема Дезарга и её применение к решению задач из курса школьной геометрии

Представленная работа посвящена теме «Теорема Дезарга и её применение к решению задач из курса школьной геометрии». Проблема данного исследования носит актуальный характер в современных условиях. Об этом свидетельствует частое изучение поднятых вопросов. Тема «Теорема Дезарга и её применение к решению задач из курса школьной геометрии» изучается на стыке сразу нескольких взаимосвязанных дисциплин. Вопросам исследования посвящено множество работ. В основном материал, изложенный в учебной литературе, носит общий характер, а в многочисленных монографиях по данной тематике рассмотрены более узкие вопросы проблемы данного исследования. Однако требуется учет современных условий при исследовании проблематики обозначенной темы. Высокая значимость и недостаточная практическая разработанность проблемы «Теорема Дезарга и её применение к решению задач из курса школьной геометрии» определяют несомненную новизну данного исследования.

Актуальность настоящей работы обусловлена, с одной стороны, большим интересом к теме «Теорема Дезарга и её применение к решению задач из курса школьной геометрии» в современной науке, с другой стороны, ее недостаточной разработанностью. Рассмотрение вопросов связанных с данной тематикой носит как теоретическую, так и практическую значимость.

Теоретическое значение изучения проблемы «Теорема Дезарга и её применение к решению задач из курса школьной геометрии» заключается в том, что избранная для рассмотрения проблематика находится на стыке сразу нескольких научных дисциплин.

Объектом данного исследования является анализ условий поставленной проблемы.

При этом предметом исследования является рассмотрение отдельных вопросов, сформулированных в качестве задач данного исследования.

Целью исследования является изучение темы «Теорема Дезарга и её применение к решению задач из курса школьной геометрии» с точки зрения новейших отечественных и зарубежных исследований по сходной проблематике. В рамках достижения поставленной цели были поставлены и решены следующие задачи:

1. Изучить теоретические аспекты и выявить природу данной темы;

2. Сказать об актуальности проблемы в современных условиях;

3. Изложить возможности решения тематики;

4. Обозначить тенденции развития тематики»;

дезарг математик теорема евклидовый

1. Исторические аспекты данной проблемы

Жерар Дезарг (Dйsargues) (1593–1662, (по др. данным – 1591–1661)), французский математик. Был военным инженером. Заложил основы проективной и начертательной геометрии. В своих исследованиях систематически применял перспективное изображение. Первым ввёл в геометрию бесконечно удаленные элементы. Дезаргу принадлежит одна из основных теорем проективной геометрии (теорема Дезарга) также сочинения о резьбе по камню и о солнечных часах, где он даёт геометрические обоснования практическим операциям. В 1636 г. Дезарг написал небольшое сочинение под заглавием «Общий метод изображения предметов в перспективе» (Париж, 1636). В этой работе он впервые применяет метод координат для построения перспективных масштабов. В качестве одной из осей он выбирает линию пересечения картинной и предметной плоскости, второй осью служит перпендикуляр к предметной плоскости, лежащий в картинной плоскости, а третьей – перпендикуляр к картинной плоскости, лежащий в предметной. Следовательно, картинная и предметная плоскости служат двумя координатными плоскостями, а третья к ним перпендикулярна. На осях координат наносятся масштабы широт, высот и глубин, при этом последний дается в перспективе. Другое сочинение Дезарга, посвященное вопросу о пересечении конуса плоскостью (1639) было утеряно и только случайно в 1845 г. французский геометр и историк математики М. Шаль нашел у одного парижского букиниста рукописную копию с этого замечательного труда. В нем Дезарг впервые рассматривает конические сечения как перспективу круга. Благодаря этому все учение о конических сечениях принимает чрезвычайно простую изящную форму, охватывая в одном методе все три вида кривых (эллипс, парабола и гипербола). Пользуясь перспективой как общим методом исследования, Дезарг пришел к необходимости рассматривать так называемые бесконечно удаленные элементы пространства. Он считал, что все параллельные прямые пересекаются в точке, которая является таким бесконечно удаленным элементом. Этим шагом Дезарг положил начало проективному представлению пространства (полное проективное пространство) и сделал возможным изучение проективных преобразований. Наконец, третьим важнейшим результатом работы Дезарга является его исследование инволюционного соответствия точек прямолинейного ряда. Здесь и самый термин «инволюция» принадлежит Дезаргу и взят им из ботанического словаря. Прямую, на которой расположен ряд точек, он называет «древом», точку отсчета отрезков – «стволом», самые отрезки – «ветвями» и т.д. Дезарг рассматривал инволюционное расположение пар точек на прямой и ему принадлежит доказательство весьма общей теоремы о том, что пучок конических сечений, проходящих через четыре неподвижных центра в пересечении с прямой дает инволюцию. Наконец, необходимо упомянуть о теореме Дезарга относительно гомологических треугольников. Фундаментальное значение этой теоремы для геометрии нельзя не заметить. Работы Дезарга заложили научные основы проективной геометрии, поэтому его следует по справедливости считать основоположником этой дисциплины.

Теорема Дезарга является фундаментальной теоремой проективной геометрии. Перед тем как сформулировать ее, дадим проективное определение треугольника.

Треугольником, или трехвершинником, или трехсторонником называется фигура, состоящая из трех точек, не лежащих на одной прямой, и трех прямых (а не отрезков прямых), соединяющих эти точки попарно (рис. 1). Точки называются вершинами, а прямые – сторонами треугольника.

В дальнейшем будем говорить о треугольниках только в смысле этого определения, если не будет оговорено противное.

Теоремы Дезарга, прямая и обратная, верны как в том случае, когда треугольники АВС и А'В'С' расположены в двух разных плоскостях, так и в том случае, когда они расположены в одной плоскости. В первом случае мы говорим о теореме Дезарга в пространстве, во втором случае о теореме Дезарга на плоскости. Точка S называется точкой Дезарга или центром перспективности, а прямая s – прямой Дезарга или осью перспективности данных треугольников. Два треугольника, удовлетворяющие условиям теоремы Дезарга в пространстве называются перспективными, так как один из них есть перспективный образ другого; два треугольника, удовлетворяющие условиям теоремы Дезарга на плоскости, называются гомологическими.

Теорема Дезарга: Если прямые проходящие через соответствующие вершины двух трехвершинников пересекаются в одной точке, то точки пересечения соответствующих сторон этих трехвершинников лежат на одной прямой. ABÇA'B'=P, ACÇA'C'=Q, BCÇB'C'=R, AA'ÇBB'ÇCC'=O.

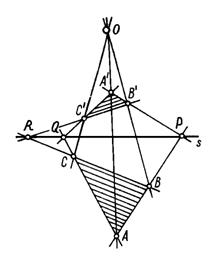
Доказательство:Рассмотрим векторы порождающие соответствующие точки, так как А, А', О лежат на одной прямой, то векторы порождающие их линейно зависимы, т.е. = .

Из того, что В', В, О – лежат на одной прямой Þ ,, - линейно зависимы Þ =

Точки С, С', О – лежат на одной прямой Þ = г +

= = г +

,, – линейно зависимы Þ точки А, В, Р Î одной прямой, ,,- линейно зависимы Þ точки А', В', Р' Î одной прямой.

P=ABÇA'B'

– = – = (2)

,, – линейно зависимы Þ точки А, С, Q Î одной прямой.

- линейно зависимы Þ точки А', С', Q' Î одной прямой.

Следовательно, Q=АСÇА'С'

– = – = (3)

,, – линейно зависимы Þ точки В, С, R Î одной прямой.

,', ' – линейно зависимы Þ точки В', С', R' Î одной прямой

Следовательно, R=ВСÇВ'С'.

Составим выражение:

=--++-=- векторы , , линейно зависимы Þ точки P, Q, R лежат на одной прямой.

Теорема доказана.

Если точки пересечения соответственных сторон двух трехвершинников лежат на одной прямой, то прямые, проходящие через соответственные вершины этих трехвершинников, проходят через одну точку.

Доказательство при помощи теоремы Менелая

Теорема Менелая гласит:

Если точки X, Y, Z лежащие на сторонах ВС, СА, АВ (соответственно продолженных) треугольника АВС коллинеарны, то

Обратно, если это уравнение выполняется для точек X, Y, Z, лежащих на трех сторонах треугольника, то эти три точки коллинеарны.

Теорема Дезарга: Если два треугольника перспективны относительно точки и если их пары соответствующих сторон пересекаются, то эти три точки пересечения коллинеарны.

Доказать: P, Q, R коллинеарны

Доказательство: Мы имеем теорему лишь о принадлежности точек прямым и пересечении прямых. Треугольники АВС и A’B’C’ перспективны относительно точки О, а пары их соответствующих сторон пересекаются в точках R, Q, P. Для доказательства применим теорему Менелая к тройкам точек. {Q, C’, A’}, {R, B’, C’}, {P, A’, B’}

Лежащих на сторонах трех треугольников ОАС, ОСВ, ОВА, получим при этом

Перемножим эти три выражения и, проделав умеренное число сокращений, получим

Þ Точки Q, R, P коллинеарны.

Теорема доказана.

Доказательство в проективной системе координат

На проективной действительной плоскости имеет место Теорема Дезарга.

Теорема Дезарга: Если прямые проходящие через соответствующие вершины двух трехвершинников пересекаются в одной точке, то точки пересечения соответствующих сторон этих трехвершинников лежат на одной прямой. P=ABÇA'B', Q=ACÇA'C', R=BCÇB'C', AA'ÇBB'ÇCC'=Q

Доказать: P, Q, R лежат на одной прямой.

Доказательство: Введем проективную систему координат, примем точки А, В, С, О за фундаментальные: А (1,0,0), В (0,1,0), С (0,0,1), О (1,1,1)

Координаты точки А' – есть линейная комбинация координат точки А и точки О, так как А¹А', то А'=aА + dq

Можно положить d=1. Тогда получаем А'=aА +q. Тоже самое относится и к другим вершинам трехвершинника A'B'C'. Поэтому А' (a+1,1,1), В' (1,+1,1), С' (1,1,g+1) уравнение прямой АВ:

АВ: х₃=0

Уравнение 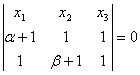А¢В¢:

А¢В¢:

Так как АВ А¢В¢=Р,

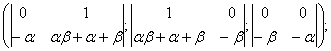P:P.

АС: 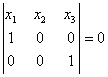, A¢C¢: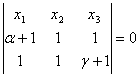

АС: х₂=0

A¢C¢:

так как АСA¢C¢=Q

Q:,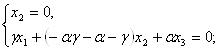

то Q

ВС: 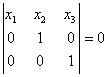, B¢C¢: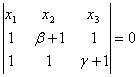

так как R=BC∩B¢C¢

R: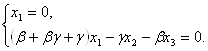, то R.

С помощью условия коллинеарности трех точек убедимся, что точки P, Q, R лежат на одной прямой.

Имеем

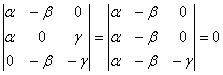
Условие коллинеарности выполнено, следовательно, P, Q, R Î одной прямой.

Теорема доказана.

2.Применение теоремы Дезарга к решению задач

2.1 Использование теоремы Дезарга на евклидовой плоскости

В аксиоматическом построении проективной плоскости мы рассматриваем теорему Дезарга, как аксиому. Покажем, что она справедлива на евклидовой плоскости. Если две одинаковые конфигурации, составленные из точек и прямых, могут быть приведены в соответствие так, что пары соответствующих точек соединяются прямыми, пересекающимися в одной точке, то мы говорим, что эти две конфигурации перспективны относительно этой точке. Если соответствие таково, что пара соответствующих прямых пересекаются в точках лежащих на одной прямой, то говорим, что эти две конфигурации перспективны относительно этой прямой.

Сформулируем теорему Дезарга, покажем использование на евклидовой плоскости. При доказательстве будем пользоваться теоремой Менелая.

Теорема Менелая гласит:

Если точки X, Y, Z лежащие на сторонах ВС, СА, АВ (соответственно продолженных) треугольника АВС коллинеарны, то (BX/CX)*(CY/AY)*(AZ/BZ)=1.

Теорема Дезарга.

Если два треугольника перспективны относительно точки и если их пары соответствующих сторон пересекаются, то эти три точки пересечения коллинеарны. Доказательство: Мы имеем теорему лишь о принадлежности точек прямым и пересечении прямых. Треугольники АВС и A’B’C’ перспективны относительно точки О, а пары их соответствующих сторон пересекаются в точке R, Q, P. Для доказательства применим теорему Менелая к тройкам точек. (Q, C’, A’), (R, B’, C’), (P, A’, B’) Лежащих на сторонах трех треугольников ОАС, ОСВ, ОВА, получим при этом (AQ/CQ)*(CC’/OC’)*(OA’/AA’)=1 (CR/BR)*(BB’/OB’)*(OC’/CC’)=1 (BP/AP)*(AA’/OA’)*(OB’/BB’)=1. Перемножим эти три выражения и проделав умеренное число сокращений, получим (AQ/CQ)*(CR/BR)*(BP/AP)=1 что точки Q, R, P коллинеарные, теорема доказана.

2.2 Примеры решения задач

№1. Доказать, что медианы треугольника пересекаются в одной точке. AA’∩BB’∩CC’=S?

Решение: Рассмотрим треугольник АВС и треугольник А1В1С1 – дезарговые треугольники, то есть треугольники удовлетворяют теореме Дезарга.

№2. В евклидовой плоскости в четырехугольник вписана трапеция, параллельные стороны которой || его диагонали. Доказать, что непараллельные стороны трапеции пересекаются на другой диагонали.

Решение: треугольники NCK и AMP дезарговые треугольники по прямой теореме Дезарга, соответствующие стороны этих треугольников пересекаются в точках, лежащих на одной прямой F, D, B, то есть точка пересечения непараллельных сторон трапеции принадлежат диагонали BD.

№3. В евклидовой плоскости противоположные вершины одного параллелограмма расположены соответственно на противоположных сторонах второго. Доказать, что оба параллелограмма имеют общий центр симметрии. Требуется доказать, что LN∩MK∩BD∩AC=S

Решение.

AC∩LN∩BD – треугольники ALD и СNB – дезарговые треугольники удовлетворяют обратной теореме Дезарга AC∩LN∩BD=S. Треугольники DKC и BMA – дезарговые треугольники по обратной теореме Дезарга MK∩BD∩AC=S. Получили AC∩BD∩MK∩LN=S. Оба параллелограмма имеют общий центр симметрии.

№4. В евклидовой плоскости дан треугольник и три параллелограмма, для каждого из которых одна сторона треугольника служит диагональю, а две другие – смежными сторонами. Доказать, что вторые диагонали этих параллелограммов пересекаются в одной точке. Требуется доказать, что AN∩BP∩CM=S. Решение: Треугольники ABC и NPM – дезарговые треугольники.

AB∩NP=Q (BC∩MP)=R (AC∩NM)=K лежат на одной несобственной прямой P по теореме обратной теореме Дезарга NA∩BP∩CM=S.

№5. В конфигурации Дезарга одну из точек выбрать за дезаргову точку. Найти в этой конфигурации вершины дезарговых треугольников и дезаргову прямую. Точка А – дезаргова точка. Треугольники A’RP и SCB – дезарговы треугольники A’S ∩ SC∩A’R=C’R∩C SB∩A’P=B’ P∩B CB∩RP=Q. Точки C’, B’, Q’S – дезаргова прямая.

№6. Прямая p лежит в плоскости треугольника АВС; К=ВС (p, L=AC (p, M=AB (p,

R=BL (CM, S=CM (AK, T=AK (BL. Доказать, что прямые AR, BS и CT пересекаются в одной точке. Требуется доказать, что AR∩BS∩CT=Q

Решение

Треугольники АВС и RST – дезарговы треугольники. RS∩AB=M TS∩BC=K точки M, K, L (по условию) TR∩AC=L. Таким образом, по теореме обратной теореме Дезарга AR∩BS∩CT=Q.

№7. Даны прямые a и b, пересекающиеся в точке S, которая лежит за пределами чертежа. Дана точка С не лежащая ни на одной из данных прямых. Построить прямую SC. Построение. Выбираем произвольно прямую s, точка A, A’ и В 1) AB (s=P, 2) P A’ (b=B’, 3) AC (s=R, 4) BC (s=Q, 5) A’R, B’Q, 6) B’Q (A’R=C’, 7) CC’ искомая прямая.

Доказательство:

Треугольники АВС и А’В’С’ – дезарговы треугольники, прямая s – дезаргова прямая. AB (A’B’=P

AC (A’C’=R (s (по построению) BC (B’C’=Q По обратной теореме Дезарга AA’ (CC’ (BB’=S.

№8. Даны две точки P и Q и не проходящая через них прямая c. Построить PQ C, не проводя PQ.

Доказательство:

Треугольники QQ1Q2 и PP1P2 – дезарговы. QQ2 (PP2=Z QQ1 (PP1=X S (по построению). Q1Q2 (P1P2=Y.

По обратной теореме Дезарга. PQ (P1Q1 (P2Q2=S (PQ (c=S искомая точка.

№9. На евклидовой плоскости даны две параллельные прямые a||b и точка С, им не принадлежащая. Через () С провести прямую, параллельную а и b.

1) Анализ: Произвольно выбираем прямую s. () А, А’ (а, () В (b. Здесь работает обратная теорема Дезарга для случая () S (– несобственная, прямая s – собственная. Треугольники АВС и А’В’С’ – построить.

2) Построение:

1) АВ (s=P

2) A’P (b=B’

3) AC (s=R

4) BC (s=Q

5) A’R, B’Q

6) A’R (B’Q=C’

7) CC’ – искомая прямая.

3) Доказательство:

Треугольники АВС и А’В’С’ – дезарговы. Формулировка обратной теоремы Дезарга.

Если прямые, содержащие соответственные стороны треугольников АВС и

А’В’С’ пересекаются в точках лежащих на одной прямой и АА’||BB’, то СС’||AA’.

По этой теореме СС’ – искомая прямая.

№10. Трапеция ABCD пересечена прямыми p и q, параллельными основанию АВ, p (AD=M, p (AC=P, q (BD=N, q (BC=Q. Доказать, что точка MN (PQ лежит на прямой АВ. Требуется доказать, что MN (PQ(AB=K.

Решение:

Рассмотрим треугольники МРА и NQB. МР (NQ=S (, так как p||q. (p (q=S() PA (BQ=C AM (BN=D

DC||p||q (DC (p(q=S((C, D, S((одной прямой по теореме обратной теореме Дезарга MN (PQ(AB=K.

Тем самым доказали, что точка МN (PQ(AB.

№11. В евклидовой плоскости даны параллелограмм АВСD, точка РCD и прямая пересекающая стороны АВ и АD. Провести прямую || l. 1) Анализ: Треугольник ANM построен. Построить треугольник СРК. Задача решается с помощью прямой теоремы Дезарга.

2) Построение:

1) NP, AC

2) NP (AC=S

3) MS (BC=K

4) KP- искомая прямая.

3) Доказательство:

треугольники ANM и CPK – дезарговы, так как AN (CP=R((AN||CP), CK (AM=Q((CK||AM) то по теореме Дезарга KP (NM=F((KP||NM.

Заключение

Работа имеет традиционную структуру и включает в себя введение, основную часть, состоящую из 2 глав, заключение и библиографический список.

Во введении обоснована актуальность выбора темы, поставлены цель и задачи исследования. Глава первая раскрывает общие вопросы, раскрываются исторические аспекты проблемы «Теорема Дезарга и её применение к решению задач». Определяются основные понятия, обуславливается актуальность звучание вопросов «Теорема Дезарга и её применение к решению задач».

В главе второй более подробно рассмотрены содержание и современные проблемы «Теорема Дезарга и её применение к решению задач».

По результатам исследования был вскрыт ряд проблем, имеющих отношение к рассматриваемой теме, и сделаны выводы о необходимости дальнейшего изучения / улучшения состояния вопроса.

Таким образом, актуальность данной проблемы определила выбор темы работы «Теорема Дезарга и её применение к решению задач», круг вопросов и логическую схему ее построения.

СПИСОК ЛИТЕРАТУРЫ

1. Атанасян Л.С., Базылев В.Т., Геометрия: Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. В 2 ч. Ч. 2. – М.: Просвещение, 1987. – 352 с.

2. Базылев, Геометрия» – М.: Просвещение, 1975

3. Вахмянина О.А., Измайлова Т.С. «Пособие по проективной геометрии» – Оренбург: ОГПИ, 1994.

4. Вилейтнер Г., История математики от Декарта до середины 19 столетия, пер. с нем., 2-е изд., – М., 1966.

5. Глаголев Н.А., Проективная геометрия: Учеб. пособие для студентов университетов, 2-е изд. – М.: Высшая школа, 1963. -344 с.

6. Ефимов «Высшая геометрия» – :Наука, 1971

7. Измайлова Т.С. Лекционный курс по проективной геометрии – Оренбург: ОГПИ, 1995.

8. Каган В.Ф., Очерки по геометрии, М.: Издательство Московского Университета, 1963. – 572 с.

9. Коксетер С.М. Новые встречи с геометрией – М.: Наука, 1978, с ил.

10. Комиссарук А.М. Проективная геометрия в задачах: Учеб. пособие для математических факультетов педагогических институтов – Минск: Высшейшая школа, 1971, 320 с.:ил.

11. Певзнер, Проективная геометрия: учеб. пособие – М.: Просвещение, 1980

12. Потоцкий Что изучает проективная геометрия – М: Просвещение, 1982

13. Хартсхорн Р., Основы проективной геометрии: Учеб. пособие для студентов университетов. – М.: Мир, 1970