Теория эллиптических интегралов и эллиптических функций

1 Общие свойства эллиптических функций

1.1 Определение эллиптической функции

1.2 Параллелограммы периодов

1.3 Основные теоремы

1.4 Эллиптические функции второго порядка

2 Примеры. Приложения

2.1 Вычисление длины дуги эллипса

2.2 Эллиптические координаты

Заключение

Библиографический список

1. Общие свойства эллиптических функций

1.1 Определение эллиптической функции

Эллиптической функцией называется мероморфная функция, допускающая периоды, которые все могут быть образованы посредством сложения и вычитания из двух первоначальных периодов 2 и 2, имеющих мнимое отношение

.

Короче говоря, мероморфная функция называется эллиптической, если она двоякопериодическая с периодами 2 и 2, отношение которых  есть мнимое число. Такая функция f(z) удовлетворяет соотношениям

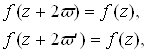 (1)

откуда вытекает, что

 (2)

где m и обозначают любые целые числа, положительные, отрицательные или нули.

Установим две формулы для эллиптической функции, из которых одна будет давать ее разложение на сумму простейших элементов с явным выделением ее полюсов и их главных частей, а другая будет представлять эллиптическую функцию посредством отношения произведений элементарных множителей с явным выделением ее нулей и полюсов. Прежде чем приступить к осуществлению этой задачи, мы установим ряд общих свойств эллиптической функции.

Примечание - при определении эллиптической функции предполагалось, что отношение

ее первоначальных периодов является мнимым числом. Если это отношение есть число действительное, то функция является просто периодической или приводится к постоянному. Кроме того, во всем дальнейшем будем считать коэффициент при мнимой части отношения  положительным, так как это достижимо путем изменения знака у одного из первоначальных периодов.

1.2 Параллелограммы периодов

Чтобы дать геометрическое истолкование двоякой периодичности, рассмотрим в плоскости комплексного переменного четыре точки

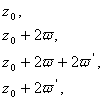
считая  произвольным комплексным числом.

Так как отношение  есть мнимое число, то эти четыре точки изображают вершины некоторого параллелограмма P.

Полагая

,

мы видим, что четыре точки, упомянутые выше, есть вершины параллелограмма , который может быть получен из основного параллелограмма  посредством некоторого сдвига.

Придавая mи всевозможные целые значения, мы получим сеть параллелограммов , конгруэнтных между собой и покрывающих всю плоскость (рис. 1).

Чтобы любые два параллелограмма нашей сети не имели общих точек, условимся причислять к каждому параллелограмму  лишь часть его границы, а именно стороны

,

,

за исключением концов

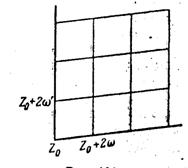
Рисунок 1 – Сеть параллелограммов

Что же касается двух сторон параллелограмма , мы их будем рассматривать принадлежащими к смежным параллелограммам с . Тогда любая точка плоскости принадлежит одному и только одному из этих параллелограммов, например .

Точки вида

,

где  и  - любые целые числа, называются конгруэнтными или эквивалентными с точкой z; в параллелограммах  они занимают то же положение, что и точка z в .

Среди этих эквивалентных точек имеется одна точка, которая принадлежит основному параллелограмму P(эта точка .

Итак, можно сказать, что всякая точка плоскости эквивалентна некоторой и притом единственной точке основного параллелограмма Р. Будем называть параллелограммы параллелограммами периодов; выбор среди них основного параллелограмма Р, очевидно, произволен. Теперь можно геометрически истолковать соотношение (2). Они выражают, что функция f(z) принимает одно и то же значение во всех эквивалентных точках. Следовательно, достаточно изучить эллиптическую функцию в одном из параллелограммов, чтобы знать ее поведение во всей плоскости.

1.3 Основные теоремы

Теорема 1. Производная эллиптической функции есть также функция эллиптическая. В самом деле, дифференцируя соотношение (1), имеющее место при любом z, получаем

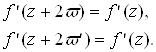
Таким образом, производная f’(z) имеет те же периоды 2 и 2, что и первоначальная функция. С другой стороны, будучи однозначной, как и f(z), f’(z) не может иметь на конечном расстоянии других особых точек, кроме полюсов, так как если f(z) голоморфна в некоторой точке, то производная f’(z) тоже голоморфна в этой точке, а если f(z) имеет полюс в некоторой точке, то и f’(z) будет иметь полюс в этой точке. Следовательно, f’(z) есть мероморфная функция, допускающая два периода 2 и 2, и согласно определению она будет эллиптической функцией с теми же периодами, что и первоначальная функция.

Теорема 2. Эллиптическая функция, отличная от постоянного, имеет по крайней мере один полюс в параллелограмме периодов.

Действительно, допуская противное, мы имели бы целую функцию, отличную от постоянного. Ее параллелограмм периодов есть ограниченная часть плоскости и в этой области, включая ее границу, наша функция голоморфна, а значит, и подавно непрерывна, а потому и ограничена. Следовательно, существует такое положительное число М, что во всем основном параллелограмме периодов имеем

Так как во всех остальных параллелограммах сети значения функции  повторяются, то неравенство |f(z)|<Mбудет справедливо для всех точек z плоскости. Итак, мы имеем целую функцию f(z) ограниченную во всей плоскости. Согласно теореме Лиувилля отсюда заключаем, что f(z) приводится к постоянному. Полученное противоречие убеждает нас в справедливости теоремы.

Следствия

1 Если две эллиптические функции с одинаковыми периодами имеют в параллелограмме периодов одни и те же полюсы с одинаковыми главными частями, то они отличаются лишь постоянным слагаемым.

В самом деле, положим, что  и  две эллиптические функции с одинаковыми периодами 2 и 2, имеющие в параллелограмме периодов одни и те же полюсы с одинаковыми главными частями. Тогда их разность - будет двоякопериодической функцией с периодами 2 и 2, без полюсов, а значит, по доказанной теореме эта разность равняется тождественно постоянному.

2 Если две эллиптические функции с одинаковыми периодами имеют в параллелограмме периодов одинаковые нули и полюсы одной и той же кратности, то они отличаются лишь постоянным множителем.

Действительно, положим, что  и  две эллиптические функции с одинаковыми периодами 2 и 2, имеющие в параллелограмме периодов одинаковые нули и полюсы одной и той же кратности.

Тогда их отношение  представляет двоякопериодическую функцию с периодами 2 и 2, причем это отношение не имеет полюсов. Следовательно, по доказанной теореме это отношение равно тождественно постоянному.

Теорема 3. Сумма вычетов эллиптической функции относительно всех полюсов, расположенных в параллелограмме периодов, равна нулю.

Прежде всего заметим, что если на границе параллелограмма периодов имеются полюсы эллиптической функции, то мы можем немного сдвинуть этот параллелограмм так, чтобы все полюсы, расположенные на первоначальном параллелограмме периодов, оказались бы внутри сдвинутого параллелограмма. Обозначим вершины этого параллелограмма через

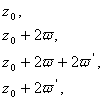
на его сторонах нет полюсов функции f(z). Согласно общей теореме о вычетах мы получим сумму вычетов S относительно всех полюсов, лежащих внутри параллелограмма, если вычислим интеграл , распространив его на периметр этого параллелограмма, проходимый в положительном направлении. Таким образом, имеем

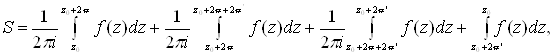 (3)

где все интегрирования совершаются по прямолинейным отрезкам, соединяющим указанные точки. Объединяя первый и третий интегралы, делаем в этом последнем подстановку

и пользуясь периодичностью, находим

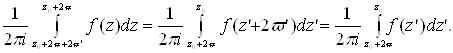
Таким образом, сумма первого и третьего интегралов выражения (3), равная

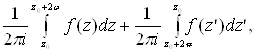
есть нуль потому, что интегрирования совершаются по одному и тому же отрезку в противоположных направлениях.

То же самое можно утверждать относительно суммы второго и четвертого интегралов, если в первом интеграле совершить подстановку

.

Возвращаясь к формуле (3), мы убеждаемся, что S равно нулю.

Теорема 4. Эллиптическая функция принимает в параллелограмме периодов всякое значение (конечное или бесконечность) одинаковое число раз. Пусть  - произвольное комплексное число. Покажем, что число корней уравнения

лежащих в параллелограмме периодов, совпадает с числом полюсов функции f(z), расположенных в этом параллелограмме. Само собой разумеется, что при счете числа нулей функции

f(z) -

или ее полюсов мы каждый нуль или полюс считаем столько раз, какова его кратность. Для доказательства нашего утверждения прежде всего заметим, что если на границе параллелограмма периодов имеются нули или полюсы функции

f(z) - ,

то мы можем немного сдвинуть этот параллелограмм так, чтобы все нули и полюсы, расположенные на первоначальном параллелограмме периодов, оказались бы внутри сдвинутого параллелограмма.

Обозначим вершины этого параллелограмма через

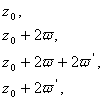
на его сторонах нет нулей и полюсов функции

f(z) -  .

Образуем вспомогательную функцию

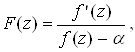
которая будет эллиптической с периодами 2 и 2, причем на сторонах рассматриваемого параллелограмма периодов она не будет иметь полюсов.

Применяя к этой функции предыдущую теорему 3, мы имеем:

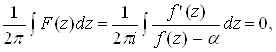 (4)

где интегрирование распространено в положительном направлении по контуру упомянутого параллелограмма. С другой стороны, как известно, интеграл

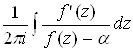
изображает разность между числом нулей и полюсов функции

f (z) - ,

лежащих внутри контура интегрирования.

Так как согласно формуле (4) этот интеграл равен нулю, то, следовательно, число корней уравнения

лежащих внутри параллелограмма периодов, совпадает с числом полюсов функции f (z), расположенных внутри того же параллелограмма. Таким образом, теорема доказана.

Если f (z) принимает в параллелограмме периодов всякое значение s раз, то она называется эллиптической функцией порядка s.

В силу теоремы 3 не может существовать эллиптической функции, имеющей в параллелограмме периодов один простой полюс. Таким образом, всегда не меньше двух, т. е. не существует эллиптических функций первого порядка. В дальнейшем мы фактически построим эллиптические функции второго порядка. Существуют, конечно, и эллиптические функции более высокого порядка.

Теорема 5. Разность между суммой всех нулей и суммой всех полюсов эллиптической функции, расположенных в параллелограмме периодов, равна некоторому ее периоду, т. е.

,

где - нули, а  - полюсы, расположенные в параллелограмме периодов. Само собой понятно, что при образовании суммы нулей или суммы полюсов

каждый нуль или полюс нужно повторить слагаемым столько раз, какова его кратность. Для доказательства прежде всего заметим, что если на границе параллелограмма периодов имеются нули или полюсы эллиптической функции, то путем небольшого сдвига этого параллелограмма мы можем достигнуть того, чтобы все нули и полюсы, расположенные на первоначальном параллелограмме периодов, попали бы внутрь сдвинутого параллелограмма. Обозначим через

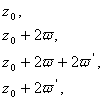
вершины этого параллелограмма. На его сторонах нет нулей и полюсов функции f (z). Тогда, как известно, искомая разность между суммами всех нулей и полюсов, расположенных внутри упомянутого параллелограмма, изображается в виде интеграла

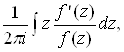
где интегрирование совершается по периметру параллелограмма в положительном направлении. Таким образом, имеем

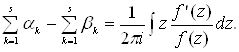 (5)

При интегрировании вдоль периметра параллелограмма сумма

приводится посредством перемены во втором интеграле z на  и

использования периодичности к следующему выражению

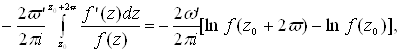
так как

,

то число в скобке есть нуль или вида

где  - целое. Таким образом, сумма двух рассматриваемых интегралов вообще равна  Аналогично сумма двух остальных интегралов

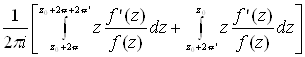
приводится посредством того же рассуждения к  Возвращаясь к формуле (5), перепишем ее в виде

что и требовалось доказать.

Примечание - применяя доказанную теорему к функции

f (z) - ,

где  - произвольное комплексное число, мы видим, что сумма корней уравнения

расположенных в параллелограмме периодов, конгруэнтна с суммой полюсов функции f (z), лежащих в этом параллелограмме, относительно ее первоначальных периодов 2 и 2.

1.4 Эллиптические функции второго порядка

1. Если эллиптическая функция f (z) с периодами 2 и 2 удовлетворяет соотношению

 (6)

где К - некоторое постоянное, то числа

будут нули или полюсы функции f (z). В самом деле, полагая в соотношении (6)

получим:

,

откуда следует, что

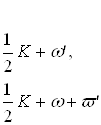
есть нули или полюсы функции f (z). Числа , ', + ' и им конгруэнтные называются полупериодами.

Предполагая К = 0, т. е. что f (z) удовлетворяет соотношению

мы будем иметь нечетную эллиптическую функцию.

В силу доказанного для такой функции точки zравной нулю, а следовательно, все периоды, равно, как все полупериоды, будут нулями или полюсами.

2. Если эллиптическая функция f (z) с периодами 2и 2' удовлетворяет соотношению

f(z) = f(K-z),         (7)

где К - некоторое постоянное, то числа

будут нули или полюсы производной f'(z). Действительно, дифференцируя соотношение (7), мы видим, что производная f'(z) удовлетворяет соотношению вида (6), откуда и следует наше утверждение вследствие утверждения 1.

В частности, если К равно нулю, т. е. если f(z) - четная функция, то ее производная будет нечетной и будет иметь нули или полюсы в точках, изображающих периоды и полупериоды. Приложим теперь эти утверждения к эллиптическим функциям второго порядка.

Обозначим через  и  полюсы такой функции, расположенные в параллелограмме периодов. Пусть сначала  неравно , т. е. оба полюса простые. В силу теоремы 5, если

то

,

откуда вытекает соотношение вида (7):

следовательно, по утверждению 1 точки

 (8)

будут нулями или полюсами производной f'(z). С другой стороны, мы знаем полюсы производной f'(z); она имеет в точках  и  полюсы второго порядка. Так как, очевидно, точки  и  не будут конгруэнтными с точками (8), то производная f'(z) должна обращаться в нуль во всех четырех точках (8). Образуем теперь функцию

которая будет эллиптической с теми же периодами, что и f(z), восьмого порядка; эта функция имеет два полюса четвертого порядка в точках  и  и нули второго порядка в четырех точках (8).

Последнее заключение сделано потому, что в точках (8) функция F (z) обращается в нуль вместе со своей производной. Заметив, что  есть эллиптическая функция с теми же периодами, что и F (z), того же порядка и с теми же нулями и полюсами, мы на основании теоремы 2 (следствие 2) заключаем:

Откуда

 (9)

Полагая

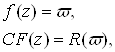
Найдем

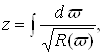 (10)

где R () - полином 4-й степени относительно . Таким образом, эллиптическая функция второго порядка

может быть рассмотрена как обращение эллиптического интеграла первого рода (10).

Пусть теперь  равно , т. е. эллиптическая функция второго порядка , имеет в точке  двойной полюс. В этом случае  удовлетворяет соотношению

точка  будет полюс третьего порядка для , ее нули расположены в точках

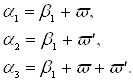
Образуем функцию

которая будет эллиптической с теми же периодами, что и , шестого порядка; эта функция имеет полюс шестого порядка в точке  и нули второго порядка в точках ,,. Последнее заключение сделано потому, что в точках ,, функция Ф (z) обращается в нуль вместе со своей производной.

Заметив, что  есть эллиптическая функция с теми же периодами, что и Ф (z), того же порядка и с теми же нулями и полюсами, мы на основании теоремы 2 (следствие 2) заключаем:

Откуда

. (11)

Полагая

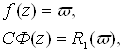
Найдем

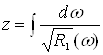, (12)

где  - полином третьей степени относительно . Таким образом,

эллиптическая функция второго порядка

и в случае двойного полюса может быть рассмотрена как обращение эллиптического интеграла первого рода вида (12).

2.  Примеры. приложения

2.1 Вычисление длины дуги эллипса

Для начала введем понятие эллиптического интеграла. Эллиптическим интегралом называется интеграл вида

 (13)

где R – рациональная функция своих аргументов и  - многочлен третьей или четвертой степени. В отдельных случаях этот интеграл может выражаться через элементарные функции, как например, интеграл

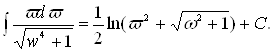
В этом случае он называется псевдоэллиптическим.

Вообще же интеграл (13) не выражается в элементарных функциях. Можно показать, что с помощью элементарных подстановок и преобразований эллиптический интеграл преобразуется к одной из трех канонических форм

 (14)

где k и l – постоянные. Интегралы (14) называют эллиптическими интегралами в форме Лежандра, соответственно, первого, второго и третьего рода. Число k называют модулем интеграла.

Подстановка

приводит интегралы (14) к тригонометрической форме

 (15)

Аргумент  называется амплитудой эллиптического интеграла. Для интегралов в форме (15) приняты следующие обозначения:

Особенно часто встречаются интегралы с амплитудой , равной ; они называются полными и для первых двух из них приняты специальные обозначения

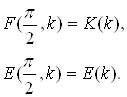
Вычисление дуги эллипса

приводит к эллиптическим интегралам. Действительно, отрезок дуги, соответствующий изменению абсциссы от 0 до x равен

Где

Это – эллиптический интеграл второго рода в форме Лежандра. Полная длина эллипса выражается через эллиптический интеграл

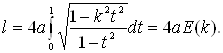 (16)

Этому обстоятельству и обязаны своим названием эллиптические интегралы, а также их обращения – эллиптические функции.

2.2 Эллиптические координаты

Эллиптические координаты также связаны с эллиптическим функциями. Чтобы ввести их, рассмотрим уравнение

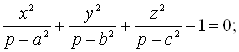
 (17)

оно третьей степени по имеет при фиксированных x, y, z три действительных корня , , , удовлетворяющих неравенству

.

Эти корни называются эллиптическими координатами точки (x, y, z). Система координат (,, ) ортогональна, так как поверхности

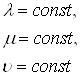
представляют собой, соответственно, софокусный эллипсоид, однополосный и двуполосный гиперболоиды, т.е. взаимно ортогональные поверхности (рис. 2).

Нетрудно вывести формулы, выражающие декартовы координаты через эллиптические. Для этого достаточно привести левую часть (17) к общему знаменателю и, заметив, что в числителе при этом получится многочлен третьей степени относительно со старшим коэффициентом -1, разложить его на линейные множители

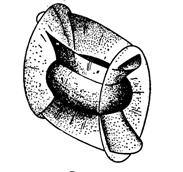
Рисунок 2

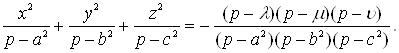
Чтобы получить (18), остается умножить обе части, соответственно, на , ,  и положить

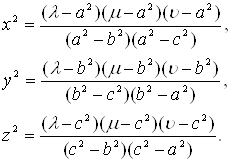 (18)

Заключение

Мы дали аналитическое представление для любой эллиптической функции, отталкиваясь от сформулированного ее дескриптивного определения. Для рациональных функций мы имеем два аналитических представления. В основе перового из них лежит задание полюсов рациональной функции и соответствующих им главных частей, что приводит нас к разложению рациональной функции на простейшие дроби. В основе второго аналитического представления рациональной функции лежит задание ее нулей и полюсов, что дает нам возможность представить ее в виде отношения произведений линейных множителей.

Библиографический список

1. Лаврентьев М.А Методы теории функций комплексного переменного/ М.А.

Лаврентьев, Б.В. Шабат. – М.: Лань, 2002 – 688 с.

2. Лунц Г.Л. Функции комплексного переменного с элементами операционного

исчисления/ Г.Л. Лунц, Л.Э. Эльсгольц. – М.: Лань, 2002 – 304 с.

3. Маркушевич А.А. Введение в теорию аналитических функций/ А.И

Маркушевич, А.А. Маркушевич. – М.: Просвещение, 1977 – 320 с.

4. Привалов И.И. Введение в ТФКП/ И.И. Привалов – М.: Высш. шк., 1999 –

432 с.

5. Эйдман В.Я. Основы теории функций комплексного переменного и

операционного исчисления/ В.Я. Эйдман. – М.: Физмат, 2002 – 256 с.