Расчет электрических полей при наличии диэлектриков. Поляризованность. Связанный заряд.

М.И. Векслер, Г.Г. Зегря

Уравнения Максвелла

div\vec{D} = \rho, rot\vec{E}=\vec{0}

(28)

и уравнение Пуассона

div(\varepsilon grad\varphi) = -\frac{\rho}{\varepsilon_0}

(29)

применимы при наличии любых диэлектриков. Следует только помнить, что ε может зависеть от координат, и его в общем случае нельзя выносить из-под знака div. Если при решении уравнения Пуассона потенциал φ найден на отдельных участках, то "сшивка" осуществляется согласно условиям

\varphi|_{x_0+} = \varphi|_{x_0-}, \left.\varepsilon|_{x_0+}\cdot\frac{{\rm d}\varphi}{{\rm d}x}\right|_{x_0+}= \left.\varepsilon|_{x_0-}\cdot\frac{{\rm d}\varphi}{{\rm d}x}\right|_{x_0-}

(30)

Теорема Гаусса как математический закон не теряет свой силы при наличии диэлектриков, но для ее практического использования не только плотность заряда ρ, но и ε должны иметь высокосимметричное распределение. Например, в случае сферической симметрии ε, как и ρ, должен зависеть только от r.

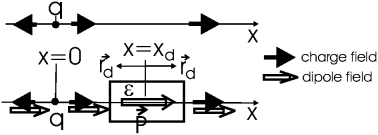
Интегрирование закона Кулона в системах с диэлектриками является недопустимым, за исключением одной искусственной ситуации. Если ε = const во всем пространстве (кроме проводников), то в задачах для вакуума просто заменяем ε0 на произведение ε0ε. В частности, для точечного заряда \vec{E} = 1/4\pi\varepsilon_0\varepsilon\cdot q\vec{r}_p/r_p^3.

Реакция диэлектрика на электрическое поле заключается в поляризации диэлектрика - ориентации дипольных моментов его молекул по полю. Количественно этот эффект тем сильнее, чем выше диэлектрическая проницаемость и чем сильнее поле. Поляризованные молекулы сами являются источниками поля, которое накладывается на внешее поле, что осложняет ситуацию даже при простой геометрии.

Подобные работы:

Актуально: