Теорема Силова

В наши дни не без основания говорят об “алгебраизации” математики, то есть о проникновении идей и методов алгебры, как в теоретические, так и в прикладные разделы всей математики.

В соответствии с принципом “важны не математические объекты, а отношения между ними” алгебра определяется как наука об алгебраических операциях, выполняемых над элементами различных множеств. Сами алгебраические операции выросли из элементарной арифметики. В свою очередь на основе алгебраических соображений получаются наиболее естественные доказательства многих факторов из “высшей арифметики” – теории чисел. теорема силов лагранж

Одной из основных типов алгебраических систем является группа. Теория групп изучает в самой общей форме свойства алгебраических операций, наиболее часто встречающихся в математике и её приложениях. Понятие группы явилось исторически одним из первых примеров абстрактных алгебраических систем и послужило во многих отношениях образцом при перестройке других математических дисциплин на рубеже XIX-XX веков, в результате которой понятие математической системы стало основным в математике.

В ряду алгебраических дисциплин составляющих совокупности, то, что иногда называют общей алгеброй, теория групп занимает, бесспорно, первое место как наиболее развита из этих дисциплин. Кроме того, теория групп представляется как область алгебры близко соприкасающийся с рядом других алгебраических теорий.

Старейшей и интенсивно развивающей ветвью теории групп, является теория конечных групп. Теорема Силова является краеугольным камнем в теории конечных групп.

Целью данной дипломной работы является изучение силовских р-подгрупп конечной группы и их свойств.

Цель обусловила постановку и решение следующих задач.

1. Изучить основные понятия теории групп.

2. Рассмотреть теорему Силова и проанализировать различные способы доказательства.

3. Представить данную тему в развернутой форме, которая в последствии может быть использована при чтении спецкурсов по теории групп.

Поставленные задачи определили структуру дипломной работы, которая состоит из введения, двух глав, заключения и списка литературы.

В первой главе собраны вспомогательные понятия и теоремы, используемые в работе, что позволило сделать изложение более доступным и замкнутым.

Во второй главе дается определение р-подгруппы, доказываются теоремы Силова, дается описание групп порядка pq и, кроме того, приводиться примеры силовских р-подгрупп.

Глава I. Дополнительные сведения

1.1 Вспомогательные понятия и утверждения

Непустое множество Gс заданной на нем бинарной алгебраической операцией * называется группой, если выполнено следующие условия:

1) замкнутость – для любого a,ÎGэлемент a*ÎG

2) ассоциативность – для любых a,,cÎG справедливо равенство (a*)*c=a* (*c) ;

3) существование нейтрального элемента – для любого aÎGсуществует элемент eÎGтакой, чтоa*e = e*a=a

4) существование обратного элемента – для любого существует элемент a^-1ÎGтакой, чтоa*a^-1=a^-1*a=e.

Подмножество Hгруппы Gназывается подгруппой, если относительно операции определенной во всей группы подмножество само является группой.

Предложение 1.1.1. Если подмножество H элементов группы Gсодержит вместе с двумя элементами a, их произведение ab и вместе с каждым элементом a его обратный a^-1, то H есть подгруппа G.

Доказательство. Надо лишь показать, что H обладает единицей, но единица G равна aa^-1 при aÎH и, следовательно, принадлежит H согласно условиям предложения. ■

Группа <G , *> называется циклической, если она состоит из всех целых степеней одного элемента aÎG, то есть G={aⁿ|Îℤ} и обозначается G=<a> – циклическая группа, порожденная элементом a .

Теорема 1.1.2.Всякая подгруппа циклической группы сама является циклической группой.

Доказательство. Действительно, если подгруппа H группы G=<g> содержит только нулевую степень элемента g, то в H имеется только один элемент – единица eгруппы G (поскольку g⁰=e). В этом случае, очевидно, H=<e>.

Если же в подгруппе H содержится какая-нибудь ненулевая степень элемента g, то в ней содержится и некоторая положительная степень g, так как вместе со всяким элементом g^k в подгруппу H входит и обратный ему элемент g^–k. Пусть – наименьшая из положительных степеней элемента g, содержащихся в H, и h=gⁿ. Покажем, что H=<h>, то есть, что H исчерпывается различными степенями элемента h:

…, h^-2, h^-1, h⁰=e, h¹, h²,….

Допустим противное, получим, что в H содержится элемент g^s и не делиться на . Но тогда можно представить в виде nq+r, где 0<r<, откуда g^s=(gⁿ)^qg^r=h^qg^r. Значит, и элемент h^–q(h^qg^r)=g^r содержится в H, а это противоречит тому, что – наименьшая из положительных степеней элемента g, содержащихся в H. ■

Из этого рассуждения следует, в частности, что любая подгруппа аддитивной группы ℤ целых чисел является либо единичной подгруппой H={0}, состоящей из единственного элемента 0, либо подгруппой H_n, состоящей из чисел, кратных некоторому целому числу ≥1:

…,-2, -, 0, , 2, ….

Напомним, что две группы G и G' с операциями * и · называется изоморфными, и обозначаются G@G', если существует отображение f:G®G' такое, что:

1. f(a*)=f(a)·f() для любых a, ÎG– отображение f сохраняет выполнимость операций в G и G', то есть отображение f –гомоморфно.

2. f – взаимнооднозначно.

Теорема 1.1.3. 1) Любая бесконечно циклическая группа изоморфна аддитивной группе целых чисел ℤ.

2) Любая конечно циклическая группа порядка изоморфна аддитивной группе классов вычетов по модулю .

Доказательство. 1) Определим отображение φ: G→ℤ, где φ(aⁿ)= , тогда:

a) Так как все целочисленные степени элемента a различны, то отображение φ(aⁿ)= является биективным или взаимнооднозначным.

b) Сохраняются операции во множествах: φ(aⁿa^k) = +k = φ(aⁿ)+φ(a^k).

Таким образом, 1) доказано.

2) G={e, a¹,…,a^n–1} – циклическая группа. Определим отображение φ таким образом: G→ℤ_n, где φ(a^k)=  для любого a^k из группы G, где kпринимает значения от 0 до -1.

a) Тогда двум равным элементам из группы G соответствуют два равных элемента из ℤ_n: из того, что a^m= a^kÛ a^m-k= eÛm-k: , по определению, m=k(mod) Û

b) Сохраняется выполнимость операций в группах: (a^ka^m)=(a^k+m)= === φ(a^m)+φ(a^k). ■

Теорема 1.1.4.Пересечение любого множества подгрупп есть подгруппа.

Доказательство.Пусть A и B– подгруппы группы <G,*>. Докажем, что H=AB– подгруппа.

1) Замкнутость H относительно умножения.

a,ÎHÞ

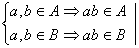
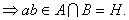
2)

3) aÎH=A ■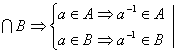

Если M– произвольная часть группы G, то пересечение (M) всех подгрупп, содержащих M, называющиеся подгруппой, порожденной множеством M, а само M– порождающим множеством подгруппы (M). Иногда говорят, что элементы множества Mявляются порождающими элементами подгруппы (M). Группа, обладающая конечным порождающим множеством, называется конечно порожденной. ■

Теорема 1.1.5. Если M– подмножество группы G, то

(M) = .

Доказательство.

Обозначим правую часть через H, так как подгруппа (M) содержит все a_iиз M, то (M)ÊH. С другой стороны, HHÍH, H^-1ÍH, поэтому H– подгруппа, содержащая M. Отсюда HÊ(M) и окончательно H=(M). ■

Если каждое соотношение в группе G относительно порождающего множества Mявляется следствием из некоторого множества соотношений Ф, то Ф – называют определяющим множеством соотношений группы G относительно порождающего множества M. Группы, имеющие конечное число определяющих соотношений, называются, конечноопределенными. Именно такие группы часто возникают в приложениях теории групп к геометрии и топологии. Иногда определяющие соотношения таковы, что элементам группы удается дать некоторую каноническую запись, и умножение элементов в канонической записи не представляет труда. Рассмотрим примеры этого рода.

Пример 1.Группа задана двумя образующими a и , связанными соотношениями a²=1(то естьa=a^-1), ³=1 и aba=². Очевидным следствием из этих соотношений является ab²a=. Последние два соотношения можно записать в форме ba=ab² и ²a=ab. Эти соотношения позволяют переносить образующий a через или ² справа налево, заменяя на ² и ² на . Это позволяет записать любой элемент группы в форме a^kb^m при k=0,1и m=0,1,2. Рассматривая элементы этого вида формально, с правилами умножения, вытекающими из правила переноса aсправа налево и условий a²=1и ³=1, нетрудно проверить, что символы a^kb^m действительно образуют группу. Она конечна, её порядок равен 6. Легко видеть, что она изоморфна симметрической группе S₃ подстановок из трех элементов. Изоморфизм дается соответствием a®(1,2), ®(1,2,3).

Пример 2. Группа задана двумя образующими c, aи соотношениями a²=1 и aca=c^-1. Здесь образующий c свободен, то есть порождает бесконечно циклическую группу. Очевидным следствием из этих соотношений является ac^ma=c^–m при любом целом m. Из соотношения ac^ma=c^-mследует правило переноса образующего a справа налево, именно, c^ma=ac^-m. Это правило позволяет записать любой элемент группы в виде a^kc^m при k=0,1 и любом целом m. Легко проследить, что символы a^kc^m при умножении с правилами, обусловленными соотношениями a²=1и c^ma=ac^-m, действительно образуют группу.

1.2 Смежные классы по подгруппе и теорема Лагранжа

п.1. Пусть в группе G дана подгруппа H. Если a есть произвольный элемент из G, то произведение aH называется левымсмежным классом группы G по подгруппе H, определенным элементомa. Аналогично дается определение правого смежного класса.

Представление группы G в виде объединения левых (правых) смежных классов по подгруппе H называется левосторонним (правосторонним) разложением группы G по подгруппе H.

G=.

Любые два левых (правых) смежных класса по одной и той же подгруппе либо не пересекаются, либо совпадают.

Предположим, что  Æ докажем, тогда что .

Имеем, Æ следовательно, существует , такой что . Тогда,  так как существует  такой что,  следовательно .

Пусть y произвольный элемент группы H. Тогда элементы xy и x^–1yÎH. Поэтому элемент cy=(ax)y=a(xy)ÎаH, а элемент ay=(cx^–1)y= =c(x^–1y) cÎH, так как каждый элемент из cH содержится в aH и наоборот, то aH=cH. Аналогично так же bH=cH и, следовательно, aH=bH.

Аналогично доказывается условие совпадения правых смежных классов: . ■

Любые два левых (правых) смежных класса по одной и той же подгруппе содержат одинаковое количество элементов.

В самом деле, докажем, что произвольный смежный класс aH содержит столько же элементов, сколько их в подгруппе H. Имеем:

,

.

Рассмотрим отображение φ: gH→H по правилу φ(gh_i)=h_i для любого h_iÎH. Заметим что

2) φ – отображение, то есть .

Действительно, .

2) отображение φ взаимно однозначно, что доказывает проведение предыдущих рассуждений в обратном порядке.

2) φ – отображение на H. В самом деле, прообразом произвольного элемента hÎH является элемент ghÎgH: φ(gh)=h. Итак, φ – взаимно однозначное отображение gHна H, отсюда следует, что gH и H содержат одинаковое количество элементов.■

Если группа G состоит из конечного числа элементов, то она называется конечной группой, а число элементов в ней порядком группы.

Теорема 1.2.1. (Лагранжа)Порядок подгруппы конечной группы является делителем порядка группы.

Доказательство.Пусть H– подгруппа конечной группы Gи  – множество всех различных левых смежных классов группы G по подгруппе H. Тогда,

G=. (1)

Причем любые два смежных класса, входящие в это объединение, не пересекаются, как было отмечено выше. Поэтому если – число элементов множества G и m– число элементов множества H, то есть число элементов в каждом левом смежном классе, то в силу (1), получаем 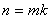 или 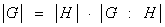, где индекс  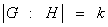– количество смежных классов в разложение (1). Теорема доказана. ■

Следствие 1. Порядок элемента конечной группы, является делителем порядка группы.

Доказательство. Пусть G– конечная группа, а его элемент порядка m. Тогда циклическая группа, порожденная элементом порядка m, имеет тоже порядок m, то есть . Отсюда по теореме 1.2.1. m является делителем порядка всей группы G. ■

Следствие 2.Пусть G– группа простого порядка, тогда G– циклическая группа (изоморфна ℤ_p).

Доказательство. Действительно, группа G совпадает с циклическойподгруппой порожденной любым её отличным от е, элементом.

п.2. Покажем, что теорему Лагранжа нельзя обратить, то есть не для любого делителя m порядка группы существует подгруппа порядка m. Например, знакопеременная группа A₄ – подстановок четной степени не содержит подгруппы порядка 6. Хотя число 6 делит её порядок равный 12. Докажем это, предварительно сформулируем утверждение.

Произвольная группа порядка 6 либо изоморфна ℤ₆, либо изоморфна группе S₃.

Доказательство.Пусть G– отличная от единичной группа,

, тогда по следствию теоремы Лагранжа, все элементы искомой группы могут иметь порядки 1, 2, 3, 6. Рассмотрим три случая.

1) Если элемент порядка 6, тогда данная группа циклическая, изоморфна ℤ₆.

2) Все неединичные элементы имеют порядок 2. Тогда группа G– абелева.

Пусть для любого элемента aÎG выполняется условие a²=e. В этом случае, если также элемент группы G, то верно равенство:

(ab)²=e, откуда, (ab)(ab)=e и a(ba)=e Умножим полученное равенство слева на a, справа на , получим ba=ab. Отсюда вытекает, что группа G– абелева.

Пусть a, элементы группы G. Несложно видеть, что множество элементов  является подгруппой группы G (достаточно проверить замкнутость и условие существование обратного элемента.) Порядок этой подгруппы равен 4. Этого быть не может по теореме Лагранжа (4 не является делителем 6). Следовательно, этот случай не имеет место.

3) Все неединичные элементы Gимеют порядок 2или 3 и есть обязательно элемент порядка 3.

Пусть a³=e, тогда a²=, ÎG и  обозначим за с – четвертый элемент группы G, отличный от трех предыдущих.

Рассмотрим произведение ec, ac, a²c. Покажем, что ac=d, a²c=f–новые элементы группы G.

· Если ac=e, тоc=a²=, противоречие с условием

· Если ac=a, то c=e, противоречие.

· Если ac=a²=, то a²a^–1=a^–1ac, или a=c, противоречие.

· Если ac=c, то a=e, противоречие.

Итак, ac=dÎG.

· Если a²c=e, то c=a противоречие.

· Если a²c=a, то c= противоречие.

· Если a²c=a², то c=e противоречие.

· Если a²c=c, то a²=e противоречие с условием a³=e.

· Если a²c=ac, то a=e противоречие.

Таким образом, группа G состоит из 6 элементов: G=.

Докажем, что c²=e. Действительно, очевидно, что c²≠ c, ac, a²c.

Если было бы c²=a (или c²=a²), то выполняется следующие c³=c²c=ac=d≠e, противоречие с условием, что все элементы группы G имеют либо второй или третий порядок (следовательно, c³=c²c=a²c=f≠e). Таким образом, ни c², ни c³не равно e, что противоречит условию. Значит c²=e.

Покажем также, что d²=f²=e, то есть c произвольный элемент не входящий в подгруппу , то d²≠a, a²(f²≠a, a²). Не сложно видеть, что d²=(ac)²≠c (иначе d=ac=), d²=(ac)²≠ac, d²=(ac)²≠a²c=f (иначе f=a²c=). Таким образом, d²=(ac)²=e и более того, a³=c²=(ac)(ac)=e.

Известно, что симметрическую группу подстановок S₃,можно задать двумя образующими и тремя определяющими соотношениями. Следующим образом S₃= где в качестве x можно взять подстановку , а в качестве y: .

Следовательно, мы можем утверждать, что . Таким образом, если G группа и , то G изоморфна либо ℤ₆, либо S₃.

Далее выпишем все элементы группы A₄и построим таблицу умножения элементов.

Все 4!=24 перестановки из четырёх символов 1, 2, 3, 4 расположим в таком порядке, чтобы каждая последующая перестановка получалась от предыдущей с помощью одной транспозиции (перемены мест двух символов).

Начнём с перестановки 1, 2, 3, 4. Итак,
.

Так как всякая транспозиция меняет четность перестановки, то в полученном ряду все перестановки, взятые через одну, являются четными (они подчеркнуты).

Теперь уже легко составить все искомые четные подстановки достаточно в каждой из них в качестве первой строки записать перестановку (1234), а в качестве второй строки одну из найденных четных перестановок. Итак,

A₄=

.

Строим таблицу умножения.

Таблица 1