Структура некоторых числовых множеств

В 1870-х годах немецкий математик Георг Кантор (1845-1918) создал теорию множеств — исключительно мощное и важное математическое учение, оказавшее огромное влияние на развитие современной математики. Теория множеств не только явилась фундаментом целого ряда новых математических дисциплин, но и оказала глубокое влияние на понимание самого предмета математики. Помимо прочего в канторовской теории множеств впервые были развиты конструктивные подходы к анализу проблемы бесконечности, более двух тысяч лет являвшейся лишь предметом филологических упражнений философов.

Теория множеств изучает общие свойства множеств, преимущественно бесконечных. Понятие множества простейшее математическое понятие, оно не поддается определению, ибо определить понятие — значит найти такое родовое понятие, в которое данное понятие входит в качестве вида, но множество — это, пожалуй, самое широкое понятие математики и логики.

Однако Кантор попытался определить данное понятие так: «Под множеством, - разъяснял Георг Кантор, - я понимаю вообще всякое многое, которое можно мыслить как единое, то есть всякую совокупность определенных элементов, которая может быть связана в одно целое с помощью некоторого закона...» ¹. Но эта концепция привела к парадоксам, в частности, к парадоксу Рассела, и данная теория стала называться наивной теорией множеств.

Парадокс Рассела — открытая в 1903 году Бертраном Расселом и позднее независимо переоткрытая Эрнестом Цермело теоретико-множественная антиномия, демонстрирующая противоречивость наивной теории множеств Г. Кантора. Антиномия Рассела формулируется следующим образом: Пусть K — множество всех множеств, которые не содержат себя в качестве своего элемента. Содержит ли K самого себя в качестве элемента? Если да, то, по определению K, оно не должно быть элементом K — противоречие. Если нет — то, по определению K, оно должно быть элементом множеств, включающихся в К — вновь противоречие.

После этого теория множеств была аксиоматизирована. На сегодняшний день множество определяется как модель, удовлетворяющая ряду аксиом (так называемая аксиоматика Цермело – Френкеля).

Множества могут состоять из самых различных элементов. Именно этим объясняется чрезвычайная широта теории множеств и ее приложимость к самым разным областям знания.

Для математики особо важную роль играют множества, составленные из математических объектов, в частности числовые множества, о которых и пойдет речь в данной работе.

При написании этой дипломной работы мы задавались целью - изучить исходные понятия и важнейшие теоремы теории множеств, а также на основании данного материала, решить ряд нестандартных задач по выявлению структуры некоторых числовых множеств.

Данная работа состоит из трех глав: «Мощности бесконечных множеств», «Точечные множества», «Решение некоторых задач».

В первой главе приводится краткое историческое описание становления теории множетсв, определяются основные понятия, такие как мощность, счетное множество, континуальное множество, с которыми нужно ознакомиться для дальнейшей работы. Устанавливаются связи между ними и доказываются основные теоремы о мощностях бесконечных множеств. В конце главы рассматривается важная теорема Шредера – Бернштейна, позволяющая проводить сравнения мощностей бесконечных множеств.

Во второй главе рассматриваются только числовые множества, т.е. множества точек числовой прямой. Вводятся основные понятия, такие как замкнутое множество, открытое множество, совершенное множество, рассматривается структура таких множеств, формулируются и доказываются основные теоремы, на основании которых, в итоге, делается важный вывод о мощности замкнутого множества.

Третья глава посвящена детальному и подробному решению ряда интересных задач (теорем) по определению структуры некоторых бесконечных числовых множеств. Также приведена задача, решение которой на первый взгляд может показаться верным, но при подробном анализе представленного доказательства можно заметить, что в решении содержится ошибочное предположение, в результате чего данное доказательство теряет свою силу. Строгое решение этой задачи также приведено в работе.

Глава 1. Мощности бесконечных множеств

§ 1. К истории становления теории множеств

С самого зарождения математической науки как самостоятельной отрасли знания и на протяжении более чем двух тысячелетий математики занимались поисками истины и добились на этом пути выдающихся успехов. Шаг за шагом древние греки, а вслед за ними и представители других цивилизаций открывали математические законы, полагая, что план, по которому построена вселенная, имеет математический характер. Необозримое множество теорем о числах и фигурах, казалось, служило неисчерпаемым источником абсолютного знания, которое никогда и никем не может быть поколеблено (4; 19). Однако по мере развития математики связь с реальным миром становится все менее ощутимой, встает вопрос о логическом обосновании математики.

В конце 19 века на передний план выступает проблема доказательства непротиворечивости математики. Движение за аксиоматизацию математики в этот период заставило математиков понять, сколь глубокая пропасть отделяет математику от реального мира. Каждая аксиоматическая система содержит неопределяемые понятия, свойства которых задаются только аксиомами. Новой теорией, которая привела к противоречиям и открыла многим глаза на противоречия, существовавшие в более старых областях математики, была теория бесконечных множеств. Первые шаги в изучении теории числовых множеств связаны с именем Георг Кантор (1845 – 1918). В 1873 г. Кантор поставил задачу классифицировать бесконечные множества. Введенные Кантором определения позволяли сравнивать два бесконечных множества по мощности. Основная идея Кантора сводилась к установлению взаимнооднозначного соответствия между множествами.

Идея взаимнооднозначного соответствия привела Кантора к неожиданному результату: он показал, что можно установить взаимнооднозначное соответствие между точками прямой и точками плоскости. Следуя принципу взаимнооднозначного соответствия, Кантор установил для бесконечных множеств отношение эквивалентности, или равенства («равномощности» двух множеств). Множество натуральных чисел и множества, которые можно поставить во взаимнооднозначное соответствие с этим множеством, содержат одинаковое число элементов, которое Кантор обозначил символом . Так как множество всех вещественных чисел больше по мощности множества натуральных чисел, Кантор обозначил его мощность новым символом – с. Возник вопрос – существует ли множество промежуточной мощности (утверждение о том, что такого множества не существует, носит название континуум гипотезы). В последствии было доказано, что в системе аксиом Цермело – Френкеля утверждение о существовании промежуточной мощности не может быть ни доказано, ни опровергнуто.

Когда Кантор в 70-х годах 19 века приступил к созданию теории бесконечных множеств и еще много лет спустя, эта теория находилась на периферии математической науки. Но к началу 20 века канторовская теория множеств нашла широкое применение во многих областях математики. Кантор и Рихард Дедекинд понимали, сколь важна теория множеств для обоснования теории целых чисел, для анализа понятий линии и размерности и даже для обоснований математики. Другие математики, в частности Эмиль Борель и Анри Леон Лебег, к тому времени уже работали над обобщением интеграла, в основу которого была положена канторовская теория множеств. Поэтому, когда сам Кантор обнаружил, что его теория множеств сопряжена с определенными трудностями, это было далеко немаловажным событием. Кантор дал несколько словесных определений множества, но эти определения не отличались строгостью, и теорию множеств в том виде, как ее изложил Кантор, нередко называют наивной. По мнению многих ученых, тщательный подбор аксиоматической основы должен был избавить теорию множеств от многих проблем и противоречий (8; 135).

Приступая к построению математики на основе теории множеств, можно выбрать ту или иную из возможных исходных позиций. Можно запретить использование гипотезы континуума, но это существенно ограничит круг теорем, доказываемых в рамках системы. Можно поступить иначе и включить в систему аксиом гипотезу континуума или ее отрицание. При этом неизвестно, к каким важным следствиям может привести отрицание гипотезы континуума. Сказанное означает, что существует не одна, а много математик. Теория множеств (рассматриваемая отдельно от остальных оснований математики) может развиваться во многих направлениях. Остановить свой выбор на одном из направлений нелегко, так как в любом случае принятие определенной редакции аксиом имеет свои положительные и отрицательные стороны.

§ 2. Счетные множества

Определение 1. Пусть А и В два множества. Правило, которое каждому элементу а множества А соотносит один и только один элемент множества В, причем каждый элемент оказывается соотнесенным одному и только одному элементу , называется взаимнооднозначным соответствием между множествами А и В.

В этом случае множества А и В называются эквивалентными или же говорят, что эти множества имеют одинаковую мощность. Обозначение

Определение 2. Пусть множество всех натуральных чисел. Всякое множество А, эквивалентное множеству , называется исчислимым, или счетным, или короче имеет мощность .

Теорема 1. Для того чтобы множество А было счетным, необходимо и достаточно, чтобы его можно было перенумеровать, т.е. представить в форме последовательности

Теорема 2. Из всякого бесконечного множества можно выделить счетное подмножество.

Теорема 3. Всякое бесконечное подмножество счетного множества счетно.

Следствие 1. Если из счетного множества А удалить конечное подмножество М, то оставшееся множество А – М будет счетным.

Теорема 4. Сумма конечного множества и счетного множества есть счетное множество.

Теорема 5. Сумма конечного числа счетных множеств есть счетное множество.

Теорема 6. Сумма счетного множества конечных множеств есть счетное множество.

Теорема 7. Сумма счетного множества счетных множеств есть счетное множество.

Теорема 8. Множество всех рациональных чисел счетно.

Доказательство

Множество дробей вида с зафиксированным знаменателем , т.е. множество

очевидно счетно

Но знаменатель может принимать также счетное множество натуральных значений. Значит, в силу теоремы 7, множество

М= - счетно

Удаляя из М все сократимые дроби и применяя теорему 3, убеждаемся в счетности всех положительных рациональных чисел , а значит в счетности всех отрицательных рациональных чисел , т.к. множества

Отсюда множество все рациональных чисел счетно, поскольку

Теорема доказана.

Следствие 1. Множество рациональных чисел любого отрезка счетно.

Теорема 9. Если к бесконечному множеству М прибавить конечное или счетное множество А новых элементов, то это не изменит его мощности, т.е.

Доказательство

Выделим, пользуясь теоремой 2, из М счетное подмножество и пусть , тогда , . Так как , , применяя теоремы 4 и 5 , получаем .

Теорема доказана.

Теорема 10. Если бесконечное множество несчетно, а А его конечное или счетное подмножество, то .

Доказательство

Множество не может быть конечным, иначе исходное множество было бы конечным или счетным. Но тогда по теореме 9, будет , а это и значит, что . Теорема доказана.

Теорема 11. Если элементы множества А определяются значками, каждый из которых, независимо от других, пробегает счетное множество значений

(, то множество А счетно.

Доказательство

Докажем теорему методом математической индукции.

Теорема очевидна, если .

Допустим, что теорема справедлива для , покажем, что она справедлива и для .

Пусть

Обозначим через множество тех элементов А, для которых , где одно из возможных значений -го значка, т.е. положим

В силу сделанного допущения множество счетно, а так как

, то счетно и А

Теорема доказана

Следствие 1. Множество точек плоскости, у которых обе координаты рациональны, счетно.

Следствие 2.Множество многочленов с целыми коэффициентами счетно.

Теорема 12. Множество алгебраических чисел счетно (6; 20).

§ 3. Мощность континуума

Теорема 1. Отрезок несчетен.

Доказательство

Допустим противное.

Пусть отрезок - счетное множество. Тогда все его точки можно расположить в виде последовательности

(1)

Пусть это сделано, т.е. всякая точка находится в последовательности (1).

Разделим на три равные части точками и (рис. 1). Ясно, что точка не может принадлежать всем трем отрезкам , , и хотя бы один из них не содержит ее. Обозначим через тот отрезок, который не содержит (если таких отрезков два, то через называем любой из них).

Рис. 1

Теперь разделим на три равных отрезка отрезок и обозначим через тот из новых отрезков, который не содержит точки .

Затем делим на три равных отрезка отрезок и обозначаем через тот из них, который не содержит точки и т.д.

В результате мы получим бесконечную последовательность вложенных друг в друга отрезков которые обладают тем свойством, что ,.

Так как длина отрезка с возрастанием стремиться к нулю, то по теореме Кантора о вложенных отрезках, существует точка , общая для всех отрезков , .

Так как , то точка должна входит в последовательность (1). Но это невозможно, ибо , . Отсюда получаем, что точка не может совпасть ни с одной из точек последовательности (1).

Теорема доказана

Определение 1. Если множество А эквивалентно отрезку то говорят, что А имеет мощность континуума, или короче, мощность с.

Теорема 2. Всякий отрезок , всякий интервал и всякий полуинтервал или имеет мощность с.

Доказательство

Пусть ,

Формула

устанавливает взаимнооднозначное соответствие между множествами и , откуда и следует, что А имеет мощность континуума.

Так как удаление одного или двух элементов из бесконечного множества приводит к множеству, эквивалентному исходному, то промежутки , , имеет ту же мощность, что и отрезок , т.е. мощность с.

Теорема доказана.

Теорема 3. Сумма конечного числа попарно не пересекающихся множеств мощности с имеет мощность с.

Доказательство

Пусть

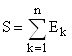где каждое из множеств имеет мощность с.

Возьмем полуинтервал и точками разложим его на полуинтервалов ,

Каждый из этих полуинтервалов имеет мощность с, так что мы можем связать множество и полуинтервал взаимнооднозначным соответствием. Легко видеть, что таким образом оказывается, установлено взаимнооднозначное соответствие между суммой и полуинтервалом

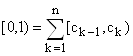
Теорема доказана.

Теорема 4. Сумма счетного множества попарно не пересекающихся множеств мощности с имеет мощность с.

Доказательство

Пусть

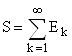где каждое из множеств имеет мощность с.

Возьмем на полуинтервале монотонно возрастающую последовательность и точками для которой .

Установив взаимнооднозначное соответствие между множествами и для всех , мы тем самым установим взаимнооднозначное соответствие между и .

Теорема доказана.

Следствие 1. Множество всех действительных чисел имеет мощность с.

Следствие 2. Множество всех иррациональных чисел имеет мощность с.

Следствие 3. Существуют трансцендентные (неалгебраические) числа.

Теорема 5. Множество всех последовательности натуральных чисел

имеет мощность .

Доказательство

Докажем теорему двумя способами:

1) Основанное на теории непрерывных дробей.

Установим взаимнооднозначное соответствие между Р и множеством всех иррациональных чисел интервала (0, 1), считая взаимосоответствующими последовательность и иррациональное число , для которого разложение в непрерывную дробь имеет вид

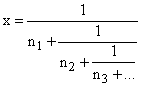Возможность соответствия и доказывает теорему.

2) Основанное на теории двоичных дробей.

Рассмотрим некоторые факты этой теории:

1. Двоичной дробью называется сумма ряда,

Указанная сумма обозначается символом

2. Всякое число допускает представление в форме

Это представление единственно в случае, когда х не есть дробь вида Числа 0 и 1 разлагаются (единственным образом) в дроби ,

Если же , то допускает два разложения. В этих разложениях знаки … совпадают, а знак в одном из них равен 1, а в другом 0. Все остальные знаки у первого разложения нули (0 в периоде), а у второго единицы (1 в периоде).

Например

3. Всякая двоичная дробь равна некоторому числу .

Если эта дробь содержит 0 или 1 в периоде, то есть число вида , исключение составляют дроби и , и тогда, наряду с исходным, существует еще одно двоичное разложение .

Если же двоичная дробь не содержит цифру 0 или 1 в периоде, то и других двоичных разложений не имеет

Вернемся к доказательству теоремы.

Условимся не пользоваться дробями, содержащими единицу в периоде. Тогда каждое число из полуинтервала будет иметь единственное представление в форме

(1)

причем, какое бы число ни взять, найдутся такие , что

Обратно, любой дроби (1) с этим свойством отвечает точка из . Но задать дробь (1) можно, указав те , для которых

Эти образуют возрастающую последовательность натуральных чисел

(2)

и каждой такой последовательности отвечает дробь (1). Значит, множество последовательностей (2) имеет мощность . Но между множествами и легко установить взаимнооднозначное соответствие. Для этого достаточно соотнести последовательности (2) последовательность

из , для которой , , ,…

Теорема доказана.

Теорема 6. Если элементы множества А определяются значками, каждый из которых, независимо от прочих значков, принимает множество значений мощностью

, то множество А имеет мощность .

Доказательство

Достаточно рассмотреть случай для трех значков, так как рассуждение имеет общий характер.

Пусть

Назовем через (соответственно, и ) множество значений значка (соответственно, и ), при этом каждый из значков изменяется независимо от прочих и каждое из множеств , имеет мощность .

Установим взаимнооднозначное соответствие между каждым из множеств , и множеством всех последовательностей натуральных чисел. Это позволит установить такое же соотношение между и .

Пусть , где , , .

В соответствиях между , и элементам , , отвечают какие-то элементы из .

Пусть

элементу отвечает последовательность ,

элементу отвечает последовательность .

Соотнесем элементу последовательность , очевидно входящую в .

Этим мы действительно получили взаимнооднозначное соответствие между А и Р, значит множество А имеет мощность .

Теорема доказана.

Следствие 1. Множество всех точек плоскости имеет мощность .

Следствие 2. Множество всех точек трехмерного пространства имеет мощность .

Следствие 3. Сумма с попарно не пересекающихся множеств мощности с имеет мощность с (6; 27).

Теорема 7. Если элементы множества А определяются с помощью счетного множества значков , каждый из которых, независимо от прочих значков, принимает множество значений мощностью , то множество А имеет мощность с.

Доказательство

Пусть множество значений значка есть .

Свяжем его взаимнооднозначным соответствием с множеством Р всех последовательностей натуральных чисел.

Пусть это соответствие обозначено .

Сделав это, выберем произвольный элемент .

Тогда , где .

Пусть в соответствии значению значка отвечает последовательность

Тогда элементу отвечает бесконечная целочисленная матрица

(*)

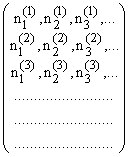Легко видеть, что полученное соответствие между А и множеством матриц (*) взаимнооднозначно. Стало быть, остается обнаружить, что множество имеет мощность с. Но это очевидно, так как, соотнеся матрице (*) последовательность

мы сразу получим взаимнооднозначное соответствие между и .

Значит множество А имеет мощность .

Теорема доказана.

Теорема 8. Множество всех последовательностей вида , где , независимо друг от друга, принимают значения 0 и 1, имеет мощность с.

Доказательство

Пусть - множество тех последовательностей из , в которых, начиная с некоторого места, все равны 1.

Каждой последовательности , входящей в , можно соотнести число, имеющее двоичное разложение ; это число будет 1 или , причем полученное соответствие между и множеством чисел указанного вида, очевидно взаимнооднозначно, откуда следует, что множество счетное.

С другой стороны, если , входящей в соотнести число с двоичным разложением , то мы получим взаимнооднозначное соответствие между и полуинтервалом (0,1), откуда вытекает, что , а значит и Т, имеют мощность с. Теорема доказана.

Следствие 1. Если элементы множества А определяются с помощью счетного множества значков, каждый из которых, независимо от прочих, принимает два значения, то множество А имеет мощность с (6; 28).

§ 4. Сравнение мощностей

Мы определили выше смысл выражений «два множества имеют одинаковую мощность», «множество имеет мощность », «множество имеет мощность с». Таким образом, встретив слово «мощность» в одном из подобных выражений, мы знаем, что оно означает, но само по себе понятие «мощность множества» у нас не определено.

Еще Г. Кантор пытался дать определение данному понятию:

«Мощностью данного множества А называется та общая идея, которая остается у нас, когда мы, мысля об этом множестве, отвлекаемся как от всех свойств его элементов, так и от их порядка» ².

В связи с этим Г. Кантор обозначал мощность множества А символом (две черты – «двойное» отвлечение).

В настоящее время канторовский способ определения понятия мощности не считается удовлетворительным (хотя обозначение оказалось очень удачным). Вместо этого принято такое формальное определение.

Определение 1. Пусть все множества разбиты по классам, так что два множества попадают в один класс тогда и только тогда, когда они эквивалентны. Соотнесем каждому такому классу множеств какой-либо символ и будем его называть мощностью любого множества данного класса. При этом, если мощность некоторого множества А есть , то пишут

При таком способе определения ясно, что эквивалентные множества действительно имеют одинаковую мощность, а также что, соотнеся классу, содержащему множество всех натуральных чисел, символ , можно сказать, что счетное множество имеет мощность .

Далее, буква с есть символ, соотнесенный классу, содержащему множество и поэтому про все множества, эквивалентные , мы говорим, что они имеют мощность с.

Пусть классу, содержащему множество , соотнесен символ «3». Тогда можно сказать, что любое множество, эквивалентное множеству А, имеет мощность 3. Мы видим, что понятие количества элементов конечного множества есть частный вид более общего понятия мощности.

Наконец, 0 есть мощность пустого множества, а 1 – мощность любого «одноэлементного» множества.

Имея, таким образом, определение понятия мощности, естественно поставить вопрос о сравнении мощностей.

Определение 2. Пусть и множества, имеющие соответственно мощности

и (, )

Если: 1) множества и не эквивалентны, но 2) в множестве В есть подмножество , эквивалентная множеству А, то говорят, что множество В имеет большую, а множество А - меньшую мощность, и пишут , .