Функции Бесселя

Цилиндрическими функциями называются решения линейного дифференциального уравнения второго порядка

, (1)

где – комплексное переменное,

– параметр, который может принимать любые вещественные или комплексные значения.

Термин «цилиндрические функции» обязан своим происхождением тому обстоятельству, что уравнение (1) встречается при рассмотрении краевых задач теории потенциала для цилиндрической области.

Специальные классы цилиндрических функций известны в литературе под названием функций Бесселя, и иногда это наименование присваивается всему классу цилиндрических функций.

Хорошо разработанная теория рассматриваемых функций, наличие подробных таблиц и широкая область применений служат достаточным основанием для того, чтобы отнести цилиндрические функции к числу наиболее важных специальных функций.

Уравнение Бесселя возникает во время нахождения решений уравнения Лапласа и уравнения Гельмгольца в цилиндрических и сферических координатах. Поэтому функции Бесселя применяются при решении многих задач о распространении волн, статических потенциалах и т. п., например:

1) электромагнитные волны в цилиндрическом волноводе;

2) теплопроводность в цилиндрических объектах;

3) формы колебания тонкой круглой мембраны;

4) скорость частиц в цилиндре, заполненном жидкостью и вращающемся вокруг своей оси.

Функции Бесселя применяются и в решении других задач, например, при обработке сигналов.

Цилиндрические функции Бесселя являются самыми распространенными из всех специальных функций. Они имеют многочисленные приложения во всех естественных и технических науках (особенно в астрономии, механике и физике). В ряде задач математической физики встречаются цилиндрические функции, в которых аргумент или индекс (иногда и тот и другой) принимают комплексные значения. Для численного решения таких задач необходимо разработать алгоритмы, позволяющие вычислять функции Бесселя с высокой точностью.

Цель курсовой работы: изучение функций Бесселя и применение их свойств в решении дифференциальных уравнений.

Задачи:

1) Изучить уравнение Бесселя и модифицированное уравнение Бесселя.

2) Рассмотреть основные свойства функций Бесселя, асимптотические представления.

3) Решить дифференциальное уравнение с использованием функции Бесселя.

1 Функции Бесселя с целым положительным значком

Для рассмотрения многих проблем, связанных с применением цилиндрических функций, достаточно ограничиться изучением специального класса этих функций, который соответствует случаю, когда параметр в уравнении (1) равен нулю или целому положительному числу.

Исследование данного класса носит более элементарный характер, чем теория, относящаяся к произвольным значениям , и может служить хорошим введением в эту общую теорию.

Покажем, что одним из решений уравнения

0, 1, 2, …, (1.1)

является функция Бесселя первого рода порядка , которая для любых значений определяется как сумма ряда

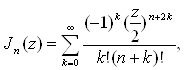
(1.2)

При помощи признака Даламбера легко убедиться, что рассматриваемый ряд сходится на всей плоскости комплексного переменного и, следовательно, представляет целую функцию от .

Если обозначить левую часть уравнения (1.1) через и ввести сокращенную запись коэффициентов ряда (1.2), положив

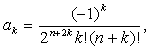
то в результате подстановки получим

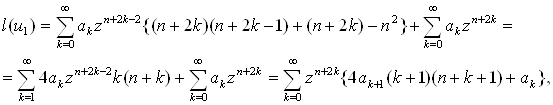
откуда следует так как выражение в фигурных скобках равно нулю. Таким образом, функция удовлетворяет уравнению (1.1), т. е. представляет собой цилиндрическую функцию.

Простейшими функциями рассматриваемого класса являются функции Бесселя порядка нуль и единица:

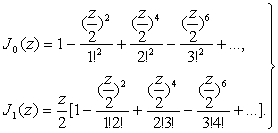(1.3)

Покажем, что функции Бесселя других порядков могут быть выражены через эти две функции. Для доказательства предположим, что а — целое положительное число, умножим ряд (1.2) на и продифференцируем по . Мы получим тогда

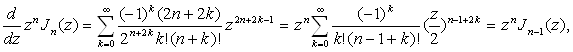
(1.4)

Аналогичным образом, умножая ряд на находим

(1.5)

Выполнив дифференцирование в равенствах (1.4 – 1.1) и разделив на множитель , приходим к формулам:

(1.6)

откуда непосредственно следует:

(1.7)

(1.8)

Полученные формулы известны под названием рекуррентных соотношений для функций Бесселя.

Первое из соотношений дает возможность выразить функцию произвольного порядка через функции порядков нуль и единица, что существенным образом сокращает работу по составлению таблиц функций Бесселя.

Второе соотношение позволяет представить производные от функций Бесселя через функции Бесселя. Для это соотношение должно быть заменено формулой

(1.9)

непосредственно вытекающей из определения данных функций.

Функции Бесселя первого рода просто связаны с коэффициентами разложения функции в ряд Лорана (1)):

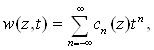
(1.10)

Коэффициенты этого разложения могут быть вычислены путем перемножения степенных рядов:

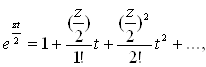
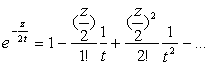
и объединения членов, содержащих одинаковые степени . Выполнив это, получим:

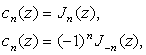
(1.11)

откуда следует, что рассматриваемое разложение может быть записано в виде

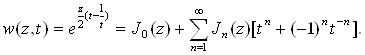(1.12)

Функция называется производящей функцией для функций Бесселя с целым значком; найденное соотношение (1.12) играет важную роль в теории этих функций.

Для получения общего интеграла уравнения (1.1), дающего выражение произвольной цилиндрической функции с целым значком , необходимо построить второе решение уравнения, линейно независимое с . В качестве такого решения может быть взята функция Бесселя второго рода, исходя из определения которой нетрудно получить для аналитическое выражение в виде ряда

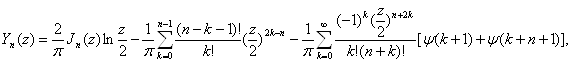(1.13)

где

( – постоянная Эйлера) и, в случае , первую из сумм надлежит положить равной нулю.

Функция регулярна в плоскости с разрезом . Существенная особенность рассматриваемого решения состоит в том, что оно обращается в бесконечность, когда . Общее выражение цилиндрической функции для представляет линейную комбинацию построенных решений

(1.14)

где и – произвольные постоянные,

2 Функции Бесселя с произвольным значком

бессель цилиндрическая функция

Функции Бесселя, рассмотренные в пункте 1, составляют частный случай цилиндрических функций более общего вида, известных под названием функций Бесселя первого рода с произвольным значком . Чтобы определить эти функции, рассмотрим ряд

где – комплексное переменное, принадлежащее плоскости с разрезом

– параметр, который может принимать любые вещественные или комплексные значения.

Легко видеть, что данный ряд сходится при любых и , причем в области , ( – произвольно большие фиксированные числа) сходимость равномерна по отношению к каждому из переменных.

Действительно, начиная с достаточного большого , отношение модулей последующего члена ряда к предыдущему, равное величине

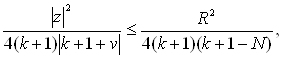
не будет превосходить некоторой правильной положительной дроби , не зависящей от и . Отсюда, согласно известному признаку сходимости, следует, что рассматриваемый ряд сходится равномерно в указанной области (4).

Так как члены ряда представляют собой регулярные функции в плоскости с разрезом сумма ряда определяет некоторую функцию комплексного переменного , регулярную в рассматриваемой разрезанной плоскости. Эта функция называется функцией Бесселя первого рода с индексом и обозначается символом . Таким образом,

(2.1)

Нетрудно показать, что определенная таким образом функция есть частное решение уравнения

(2.2)

Действительно, обозначая левую часть этого уравнения и полагая , мы находим, так же как в пункте 1,

где – коэффициенты ряда (2.1),

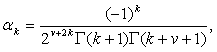
откуда следует, что

Так как при фиксированном , принадлежащем плоскости с разрезом члены ряда (2.1) представляют собой целые функции переменного , то из равномерной сходимости по отношению к этому переменному вытекает, что функция Бесселя первого рода, рассматриваемая как функция своего значка, есть целая функция . При целом и ряд (2.1) переходит в ряд (1.2), поэтому функции, определенные в настоящем параграфе, являются обобщением функций Бесселя с целым положительным значком, изученных в пункте 2. При равном целому отрицательному числу , первые членов ряда (2.1) обращаются в нуль, и рассматриваемая формула может быть записана в виде

откуда следует

(2.3)

Таким образом, функции Бесселя с отрицательным целым значком отличаются от соответствующих функций с положительным значком только постоянным множителем.

Полученное соотношение вместе с формулами (1.10 – 1.11) показывает, что разложение (1.12) может быть записано в виде

(2.4)

Многие равенства, установленные ранее для функций Бесселя с целым положительным значком, переносятся на функции с произвольным индексом без каких-либо изменений. Так, например, имеют место соотношения:

(2.5)

(2.6)

(2.7)

представляющие собой обобщение соответствующих формул пункта 2. Доказательство формул (2.5 – 2.6) повторяет рассуждения этого параграфа и поэтому не приводится. Формулы (2.7) получаются путем повторного применения равенств (2.6).

3 Общее представление цилиндрических функций. Функции Бесселя второго рода

По определению цилиндрическая функция есть произвольное решение дифференциального уравнения второго порядка

(3.1)

поэтому общее ее выражение содержится в форме

(3.2)

где и – какие-либо линейно независимые решения рассматриваемого уравнения, и – постоянные, являющиеся, вообще говоря, произвольными функциями параметра . Легко получить общее выражение цилиндрической функции для случая, когда отлично от целого числа. Действительно, выбрав , где – функция Бесселя, определенная в пункте 2, мы можем взять в качестве функцию , которая также является решением уравнения (3.1), так как последнее не меняется при замене на .

Если не равно целому числу, асимптотическое поведение рассматриваемых решений при будет

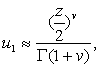
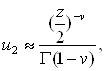(3.3)

поэтому эти решения линейно независимы между собой и искомое выражение для цилиндрической функции может быть дано в виде

(3.4)

Если – целое число, то, в силу соотношения (2.3), построенные частные решения линейно зависимы между собой и найденное выражение (3.4) не является общим интегралом уравнения Бесселя (3.1). Чтобы получить представление произвольной цилиндрической функции, пригодное при любых значениях параметра , введем в рассмотрение функцию Бесселя второго рода , которую для произвольных , принадлежащих плоскости с разрезом , определим при помощи равенства

(3.5)

При равном целому числу правая часть рассматриваемого выражения приобретает неопределенный вид (2.3), и мы условимся понимать под значением функции в этом случае предел

(3.6)

Так как по доказанному числитель и знаменатель в (3.5) суть целые функции , рассматриваемый предел существует, и может быть вычислен по правилу Лопиталя, применение которого дает

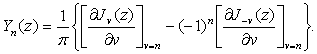(3.7)

Из определения функции следует, что эта функция регулярна в плоскости с разрезом , а при фиксированном представляет собой целую функцию параметра . Докажем теперь, что удовлетворяет уравнению (3.1), следовательно, является цилиндрической функцией. При , отличном от целого числа, требуемый результат непосредственно вытекает из формулы (3.4), поэтому достаточно провести доказательство только для случая

Проще всего воспользоваться для этого принципом аналитического продолжения. Так как – целая функция , то из равенства следует

Решения и линейно независимы между собой. Для этот результат является следствием линейной независимости решений и . Линейная независимость для вытекает из сопоставления поведения рассматриваемых функций при (формулы (3.3) и (3.4)). Таким образом, общее выражение цилиндрической функции, пригодное при любых значениях , будет

(3.8)

Функции Бесселя второго рода удовлетворяют тем же рекуррентным соотношениям, что и функции первого рода, именно:

(3.9)

При , отличном от целого числа, справедливость этих формул вытекает из определения функции Бесселя второго рода и соответствующих формул для функций первого рода. Для целого требуемый результат следует из непрерывности рассматриваемых функций по отношению к значку , что позволяет осуществить в соотношениях (3.9) предельный переход

Отметим еще формулу

(3.10)

являющуюся следствием (3.7) и позволяющую свести вычисление функций с отрицательным целым значком к вычислению функций, индекс которых положителен.

При помощи замены переменных в уравнении (3.1) легко получить ряд других дифференциальных уравнений, общий интеграл которых может быть выражен через цилиндрические функции. Наиболее интересные для приложений уравнения этого типа являются различными частными случаями дифференциальных уравнений

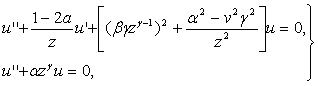(3.11)

общие интегралы которых соответственно будут:

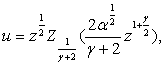(3.12)

где обозначает произвольную цилиндрическую функцию.

4 Разложение в ряд функции Бесселя второго рода с целым значком

Для того чтобы получить разложение в ряд функции , достаточно воспользоваться формулой (3.7) и вычислить производные по значку , исходя из разложения (2.1), причем, ввиду соотношения (3.10), можно ограничиться рассмотрением случая целых положительных

Так как ряд (2.1), по доказанному, сходится равномерно по отношению к , мы можем дифференцировать его почленно и получим тогда (2)

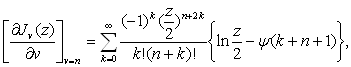
где – логарифмическая производная гамма-функции.

Аналогично имеем

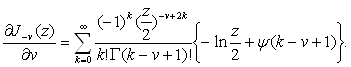
При и поэтому первые членов ряда принимают неопределенный вид. Воспользовавшись известными формулами теории гамма-функции

;

получим для таких

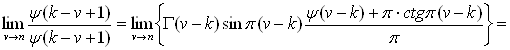
поэтому

где введен новый значок суммирования

Из формулы (3.7) следует, что искомое разложение функции Бесселя второго рода с целым положительным значком имеет вид

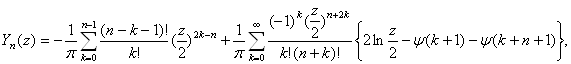
(4.1)

где в случае первую сумму надлежит положить равной нулю.

Значения логарифмической производной гамма-функции могут быть вычислены по формулам:

(4.2)

где – постоянная Эйлера,

Принимая во внимание равенство (1.2), мы можем представить разложение (4.1) в несколько другом виде, именно:

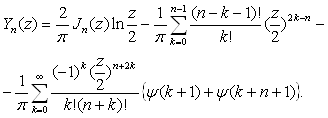(4.3)

Из (4.1) вытекает, что при справедливы асимптотические формулы

(4.4)

показывающие, что когда

5 Функции Бесселя третьего рода

К цилиндрическим функциям относятся также функции Бесселя третьего рода или функции Ханкеля и , которые для произвольного и , принадлежащего плоскости с разрезом вдоль полуоси , определяются при помощи формул

(5.1)

где – функции Бесселя первого и второго рода.

Целесообразность введения этих функций обусловлена тем, что рассматриваемые линейные комбинации из и обладают наиболее простыми асимптотическими разложениями при больших (пункт 8) и часто встречаются в приложениях.

Из определения функций Ханкеля следует, что эти функции представляют собой регулярные функции в плоскости с разрезом и целые функции . Очевидно, что рассматриваемые функции линейно независимы между собой и по отношению к , так что общий интеграл уравнения Бесселя (3.1) может быть, наряду с (3.8), представлен в одной из следующих форм:

(5.2)

где – произвольные постоянные.

Являясь линейными комбинациями функций и , функции Ханкеля удовлетворяют тем же рекуррентным соотношениям, что и эти функции, например,

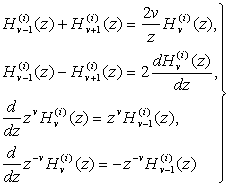(5.3)

и т.д.

Если с помощью (3.5) исключить из (5.1) функцию Бесселя второго рода, то получим

(5.4)

откуда вытекают важные соотношения:

(5.5)

6 Функции Бесселя мнимого аргумента

С функциями Бесселя тесно связаны две часто встречающиеся в приложениях функции и , которые для , принадлежащего плоскости с разрезом вдоль отрицательной полуоси и произвольного , могут быть определены при помощи формул:

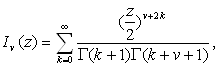
(6.1)

(6.2)

и при целом

(6.3)

Повторяя рассуждения пункта 2, получаем, что и представляют собой регулярные функции в плоскости с разрезом и целые функции .

Рассматриваемые функции просто связаны с функциями Бесселя от аргумента .

Действительно, предположим, что . Тогда и из (2.1) следует

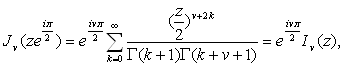
откуда

(6.4)

для всех

Аналогично из формулы (5.4) получаем для таких же

откуда

(6.5)

Для значений функции и могут быть выражены через функции Бесселя от аргумента . Мы имеем

(6.6)

для всех .

На основании полученных соотношений функции и называются функциями Бесселя мнимого аргумента. Функция известна в литературе также под названием функции Макдональда.

Из выведенных формул непосредственно следует, что рассматриваемые функции представляют собой линейно независимые решения дифференциального уравнения

(6.7)

которое отличается от уравнения Бесселя только знаком одного члена и переходит в него при подстановке .

Уравнение (6.7) часто встречается в математической физике. Общий интеграл этого уравнения при произвольном может быть записан в виде

(6.8)

Функции и удовлетворяют простым рекуррентным соотношениям:

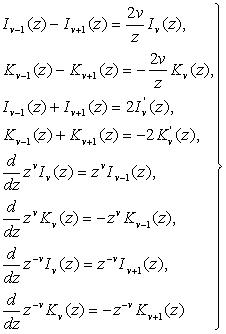(6.9)

и т.д.

Рекуррентные формулы, содержащие функции , доказываются подстановкой в них ряда (6.1). Соответствующие формулы для функций при , отличном от целого числа, проверяются путем подстановки в них выражения (6.2) и использования формул первой группы. Справедливость последних соотношений при целом следует из непрерывности рассматриваемых функций по отношению к значку.

Укажем еще две полезные формулы:

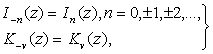(6.10)

первая из которых вытекает из (6.1), если принять во внимание, что при первые членов разложения обращаются в нуль, в то время как вторая является прямым следствием определения функции Макдональда (6.2).

Разложение функции при может быть получено из (6.3) методом пункта 5. Приведем окончательный результат вычисления:

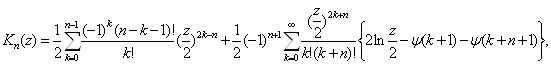(6.11)

Здесь – логарифмическая производная гамма-функции, значения которой могут быть найдены по формулам (4.2). Для случая первую из сумм надлежит считать равной нулю.

Из (6.11) вытекает, что асимптотическое поведение функции при определяется формулами

(6.12)

поэтому

7 Цилиндрические функции с индексом, равным половине нечетного целого числа

Специальный класс цилиндрических функций образуют цилиндрические функции с индексом, равным половине нечетного целого числа. В рассматриваемом случае цилиндрические функции могут быть выражены через элементарные функции. Чтобы показать это, найдем предварительно значения функций , для чего положим в (2.1) и воспользуемся для преобразования рядов формулой удвоения гамма-функции

Мы получим тогда

(7.1)

и аналогично

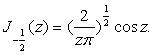(7.2)

Возможность выразить функцию Бесселя первого рода с любым полуцелым значком через элементарные функции следует теперь из рекуррентной формулы (2.5)

пользуясь которой можно последовательно получить:

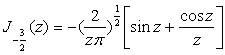
и т. д.

Общее выражение для через элементарные функции получается из формул (2.7). Например, если положить во второй из них и воспользоваться результатом (7.1), то находим:

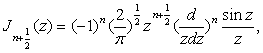
(7.3)

Соответствующие формулы для функций Бесселя второго и третьего рода могут быть выведены из найденных соотношений, если воспользоваться выражениями этих функций через функции Бесселя первого рода (3.5 и 5.4). Например, мы имеем:

(7.4)

и т. д.

В заключение укажем на формулы:

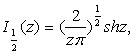
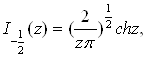
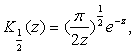(7.5)

вытекающие из определений рассматриваемых функций (6.1 – 6.2).

Формулы для других полуцелых значений индекса получаются из этих формул с помощью рекуррентных соотношений (6.9). Лиувиллем доказано, что случай полуцелого индекса является единственным, когда цилиндрические функции приводятся к элементарным.

8 Асимптотические представления цилиндрических функций для больших значений аргумента

Цилиндрические функции обладают простыми асимптотическими представлениями, удобными для аппроксимации этих функций при больших по модулю значениях и фиксированном значении индекса (5). Главные члены этих формул можно получить, исходя из дифференциальных уравнений, которым удовлетворяют рассматриваемые функции.

Из цилиндрических функций наиболее простые асимптотические представления имеют функции третьего рода.

Чтобы получить асимптотическое представление функции , воспользуемся равенством

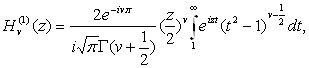
(8.1)

и преобразуем его с помощью подстановки . Тогда получим

(8.2)

Заменяя множитель биноминальным разложением с остаточным членом

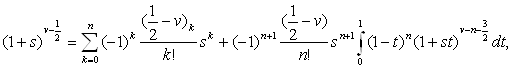
и интегрируя почленно, находим

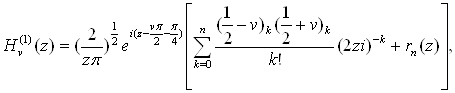(8.3)

где

Предположим, что ( – произвольное малое положительное число) и будем временно считать, что выбрано так, что Оценка остаточного члена по модулю тогда дает

при фиксированном

Таким образом, для больших

(8.4)

Покажем, что условие, наложенное на , может быть отброшено. Действительно, если , то можно выбрать такое , что . Представив с помощью формулы (8.4), где заменено на , и замечая, что

мы снова приходим к прежнему результату.

Также легко с помощью соотношения освободиться от ограничения, наложенного на параметр .

Наконец