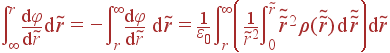Уравнение Пуассона. Его применение для расчета полей в вакууме

М.И. Векслер, Г.Г. Зегря

Уравнение Пуассона для ε = 1 выглядит:

\Delta \varphi = - \frac{\rho}{\varepsilon_0}

(16)

Это уравнение - основа практических численных расчетов.

В задачах, решаемых аналитически, φ и ρ обычно зависят только от одной координаты. При интегрировании можно вычислять интегралы как неопределенные, не забывая выписывать +const, а затем отдельно находить эти константы. Если раccматриваются отдельные диапазоны координат, то на незаряженных границах необходимо "сшивать" потенциал: φ и - для вакуума - d φ/dx (или dφ/dr) не должны иметь разрыва. Если граница заряжена (σ), то dφ/dx испытывает скачок на величину –σ/ε0. Кроме того, если ρ и суммарный заряд конечны, то φ всюду конечен.

Другой вариант - сразу правильно писать пределы интегрирования. Для этого используется известное (или очевидное из симметрии задачи) значение поля (-\nabla\varphi) в одной какой-либо точке и значение потенциала в какой-либо точке (не обязательно в той же, где знаем поле). Если в задаче не оговорено иное, то следует принимать φ|∞ = 0. Так, например, для случая зависимости потенциала только от одной сферической координаты r

\frac{1}{r^2}\frac{{\rm d}}{{\rm d}r}\left( r^2\frac{{\rm d}\varphi}{{\rm d}r}\right) = -\frac{\rho(r)} {\varepsilon_0}

(17)

после переноса r2 в правую часть и двух последовательных интегрирований получаем:

\frac{{\rm d}\varphi}{{\rm d}r}

=

-\frac{1} {\varepsilon_0r^2} \int\limits_{0}^r\tilde{r}^2 \rho(\tilde{r}) {\rm d}\tilde{r}

(18)
φ(r)=

\int\limits_{\infty}^r \frac{{\rm d}\varphi}{{\rm d}\tilde{r}} {\rm d}\tilde{r} = -\int\limits_r^{\infty}\frac{{\rm d}\varphi}{{\rm d}\tilde{r}} {\rm d}\tilde{r} = \frac{1}{\varepsilon_0} \int\limits_r^{\infty} \left( \frac{1}{\tilde{r}^2} \int\limits_0^{\tilde{r}} \tilde{\tilde{r}^2} \rho(\tilde{\tilde{r}}) {\rm d} \tilde{\tilde{r}}\right){\rm d}\tilde{r}

(19)

При этом взято φ|r = ∞ = 0 и учтено то обстоятельство, что при всюду конечном ρ поле в центре равно нулю (–dφ/dr|r = 0 = 0).

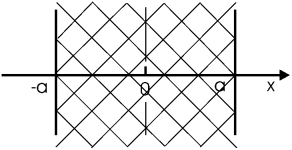
Задача. Пластина ширины 2a (ее ε≈ 1) заряжена равномерно по объему (ρ(x) = ρ0); при x = 0 (центр пластины) φ = 0. Найти φ(x).

Ответ: \varphi(x)=-\frac{\rho_0x^2}{2\varepsilon_0}, |x|, |x|>a

Подобные работы:

Актуально: