Теоремы Силова
Строение абелевых групп во многом определяется строением максимальных р-подгрупп. В теории конечных групп максимальные подгруппы также играют существенную роль. Теорема, доказанная норвежским математиком Л. Силовом в 1872 году, явилась краеугольным камнем теории конечных групп. Она неоднократно обобщалась в разных направлениях как в нашей стране (С. А. Чунихин и др.), так и за рубежом (Ф. Холл и др.). В связи с этой теоремой и в честь ее автора максимальные р-подгруппы конечных (а часто и бесконечных) групп называются силовскими р-подгруппами. Проблема нахождения силовской подгруппы данной группы является важной задачей вычислительной теории групп. Для групп перестановок Уильям Кантор доказал, что силовская p-подгруппа может быть найдена за время, полиномиальное от размера задачи (в данном случае это порядок группы, помноженный на количество порождающих элементов).
Говорят, что группа G действует на множестве М, если для каждых элементов![]() ,
, ![]() определен элемент
определен элемент ![]() , причем
, причем ![]() и me=m для всех
и me=m для всех ![]() ,
, ![]() ; здесь e — единица группы G. Множество
; здесь e — единица группы G. Множество ![]() называется орбитой элемента m. Очевидно, орбиты любых двух элементов из М либо совпадают, либо не пересекаются, так что множество М разбивается на непересекающиеся орбиты. Людвиг Силов (норв. Peter Ludvig Mejdell Sylow — фонетически правильней транслитерация «Сюлов»; 1832—1918) — норвежский математик. Автор нескольких работ по теории эллиптических функций и по теории групп. С 1858 по 1898 годы был учителем в школе в городе Фредериксхальд. В 1862 году Силов заменил профессора по теории Галуа в университете Христиании, где он поставил задачу, которая привела к наиболее важному результату его жизни — так называемым теоремам Силова, опубликованным в 1872 году.
называется орбитой элемента m. Очевидно, орбиты любых двух элементов из М либо совпадают, либо не пересекаются, так что множество М разбивается на непересекающиеся орбиты. Людвиг Силов (норв. Peter Ludvig Mejdell Sylow — фонетически правильней транслитерация «Сюлов»; 1832—1918) — норвежский математик. Автор нескольких работ по теории эллиптических функций и по теории групп. С 1858 по 1898 годы был учителем в школе в городе Фредериксхальд. В 1862 году Силов заменил профессора по теории Галуа в университете Христиании, где он поставил задачу, которая привела к наиболее важному результату его жизни — так называемым теоремам Силова, опубликованным в 1872 году.
ГЛАВА 1. ТЕОРЕМЫ СИЛОВА
Пусть G – конечная группа, а р – простое число, которое делит порядок G. Подгруппы порядка pt называются р-подгруппами. Выделим из порядка группы G примарный делитель по р, то есть | G | = pns , где s не делится на р. Тогда силовской р-подгруппой называется подгруппа G, имеющая порядок pn. Под N(P) понимается нормализатор подгруппы Р в G.
Теорема 1.(первая теорема Силова).
Силовские р-подгруппы существуют.
Доказательство.
Докажем теорему индукцией по порядку G. При |G| = p теорема верна. Пусть теперь |G| > p. Пусть Z(G) - центр группы G. Возможны два случая:
а) p делит |Z|. Тогда в центре существует циклическая группа ![]() (как элемент примарного разложения центра), которая нормальна в G. Факторгруппа G по этой циклической группе имеет меньший порядок, чем G, значит, по предположению индукции, в ней существует силовская p-подгруппа. Рассмотрим её прообраз в G. Он и будет нужной нам силовской p-подгруппой G.
(как элемент примарного разложения центра), которая нормальна в G. Факторгруппа G по этой циклической группе имеет меньший порядок, чем G, значит, по предположению индукции, в ней существует силовская p-подгруппа. Рассмотрим её прообраз в G. Он и будет нужной нам силовской p-подгруппой G.
б) p не делит |Z|. Тогда рассмотрим разбиение G на классы сопряжённости:![]() (поскольку если элемент лежит в центре, то его класс сопряжённости состоит из него одного). Порядок G делится на p, значит, должен найтись класс Ka, порядок которого не делится на p. Соответствующий ему нормализатор имеет порядок pnr, r < s. Значит, по предположению индукции, в нём найдётся силовская p-подгруппа — она и будет искомой.
(поскольку если элемент лежит в центре, то его класс сопряжённости состоит из него одного). Порядок G делится на p, значит, должен найтись класс Ka, порядок которого не делится на p. Соответствующий ему нормализатор имеет порядок pnr, r < s. Значит, по предположению индукции, в нём найдётся силовская p-подгруппа — она и будет искомой.
Теорема 2.(вторая теорема Силова).
Всякая p-подгруппа содержится в некоторой силовской p-подгруппе. Все силовские p-подгруппы сопряжены (т.е. каждая представляется в виде gPg − 1, где g — элемент группы, а P — силовская подгруппа из теоремы 1).
Доказательство
Итак, пусть силовские р-подгруппы в G существуют и Р — одна из них. Пусть, далее, ![]() — произвольная р-подгруппа группы G, не обязательно силовская. Заставим
— произвольная р-подгруппа группы G, не обязательно силовская. Заставим ![]() действовать левыми сдвигами на множестве
действовать левыми сдвигами на множестве ![]() левых смежных классов G по Р. Длина любой орбиты относительно
левых смежных классов G по Р. Длина любой орбиты относительно ![]() делит порядок
делит порядок ![]() ,
,![]() . Таким образом,
. Таким образом,
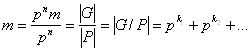
где![]() ,... — длины орбит. Так как НОД(m,p) = 1, то хотя бы одна орбита имеет длину pki = 1, т. е.
,... — длины орбит. Так как НОД(m,p) = 1, то хотя бы одна орбита имеет длину pki = 1, т. е.
![]() (1)
(1)
для некоторого элемента![]() . Переписав соотношение (1) в виде
. Переписав соотношение (1) в виде![]() , мы приходим к заключению, что
, мы приходим к заключению, что
![]() (2)
(2)
(поскольку ![]() — группа). В частности, если
— группа). В частности, если ![]() — силовская р-подгруппа, то |
— силовская р-подгруппа, то |![]() | = |Р|, и из (2) следует, что
| = |Р|, и из (2) следует, что ![]() =
=![]() .
.
Теорема 3(третья теорема Силова).
Количество силовских p-подгрупп сравнимо с единицей по модулю p ![]() и делит порядок G.
и делит порядок G.
Доказательство.
Рассмотрим несколько более общую ситуацию. Именно, пусть ![]() , где
, где ![]() , t может делится на p, и пусть
, t может делится на p, и пусть ![]() - число всех подгрупп порядка
- число всех подгрупп порядка ![]() в G. Оказывается, что имеет место сравнение
в G. Оказывается, что имеет место сравнение ![]() , в частности, G содержит подгруппы любого порядка
, в частности, G содержит подгруппы любого порядка ![]() , s=1,2,…,n и
, s=1,2,…,n и ![]() .
.
Рассуждаем следующим образом. Действие левыми сдвигами группы G на себе индуцирует действие G на множестве
![]()
всех ![]() -элементных подмножеств
-элементных подмножеств ![]() . Причём
. Причём ![]() . Множество
. Множество ![]()
![]() разбивается на G-орбиты
разбивается на G-орбиты ![]() , так что
, так что
![]() ,
, ![]()
где ![]() - стационарная подгруппа некоторого представителя
- стационарная подгруппа некоторого представителя ![]() .
.
Так как ![]() , то
, то ![]() - объединение нескольких правых смежных классов G по
- объединение нескольких правых смежных классов G по ![]() . Поэтому
. Поэтому ![]() , откуда
, откуда ![]() . В случае
. В случае ![]() имеем
имеем ![]() . Равенства
. Равенства ![]() и
и ![]() эквивалентны. Получаем
эквивалентны. Получаем
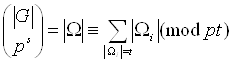
![]() (
(![]() - некоторый элемент из G) и, стало быть,
- некоторый элемент из G) и, стало быть, ![]() - подгруппа порядка
- подгруппа порядка ![]() . Орбита
. Орбита ![]() исчерпывается некоторым числом левых смежных классов
исчерпывается некоторым числом левых смежных классов ![]() группы G по
группы G по ![]() .
.
Обратно: каждая подгруппа ![]() порядка
порядка ![]() приводит к орбите
приводит к орбите ![]() длины t. Различные подгруппы
длины t. Различные подгруппы ![]() с
с ![]() приводят к различным орбитам
приводят к различным орбитам ![]() , поскольку из
, поскольку из ![]() следует
следует ![]() , откуда
, откуда ![]() и
и ![]() . Таким образом, имеется взаимно однозначное соответствие между подгруппами порядка
. Таким образом, имеется взаимно однозначное соответствие между подгруппами порядка ![]() и орбитами
и орбитами ![]() длины t. Тогда сравнение записывается как
длины t. Тогда сравнение записывается как

Где следовало бы написать ![]() , чтобы подчеркнуть зависимость
, чтобы подчеркнуть зависимость ![]() от G.
от G.
Если взять за G циклическую группу порядка ![]() , то для неё
, то для неё ![]() и поэтому
и поэтому

Так как левые часть сравнений по одному и тому же модулю совпадают, то имеем
![]()
А это и даёт искомое сравнение
![]()
Получим полезное уточнение теорем Силова.
Теорема 4.
Справедливы следующие утверждения:
1).силовская p-подгруппа P группы G нормальна в G тогда и только тогда, когда ![]()
2).конечная группа G порядка ![]() является прямым произведением своих силовских
является прямым произведением своих силовских ![]() - подгрупп
- подгрупп ![]() в точности тогда, когда все эти подгруппы нормальны в G.
в точности тогда, когда все эти подгруппы нормальны в G.
Доказательство.
1).Все силовские подгруппы, отвечающие данному простому делителю р порядка ![]() , по второй теореме Силова сопряжены, и если P–одна из них, то
, по второй теореме Силова сопряжены, и если P–одна из них, то
![]()
![]() нормальна в G
нормальна в G
2).Если ![]() - прямое произведение своих силовских подгрупп, то
- прямое произведение своих силовских подгрупп, то ![]() нормальна в G как любой прямой множитель. Значит условие нормальности необходимо.
нормальна в G как любой прямой множитель. Значит условие нормальности необходимо.
Пусть теперь ![]() нормальна в G,
нормальна в G, ![]() , т.е.
, т.е. ![]() . Заметим, что
. Заметим, что ![]() . Стало быть,
. Стало быть, ![]() , а отсюда для любых
, а отсюда для любых ![]() имеем
имеем
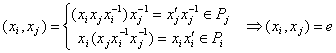
Т.е. элементы ![]() и
и ![]() перестановочны.
перестановочны.
Представим, что единичный элемент ![]() записан в виде
записан в виде ![]() , где
, где ![]() - элемент порядка
- элемент порядка ![]() . Положив
. Положив ![]() и воспользовавшись перестановочностью
и воспользовавшись перестановочностью ![]() получим
получим
![]()
Но так как а и ![]() взаимно просты, то
взаимно просты, то ![]() . Это верно при любом j, и, стало быть, равенство
. Это верно при любом j, и, стало быть, равенство ![]() возможно лишь при
возможно лишь при ![]()
С другой стороны, каждый элемент ![]() порядка
порядка ![]() ,
, ![]() записывается в виде
записывается в виде ![]() ,
, ![]() ,
, ![]() . Достаточно положить
. Достаточно положить ![]() , где показатели определяются условиями
, где показатели определяются условиями
теорема силов конечная группа
![]() ,
, ![]()
Если теперь ![]() - другая запись x в виде произведения
- другая запись x в виде произведения ![]() -элементов, то в силу перестановочности
-элементов, то в силу перестановочности ![]() ,
, ![]() с различными нижними индексами будем иметь
с различными нижними индексами будем иметь
![]() ,
,
что, как было показано выше, влечёт равенства
![]() , т.е.
, т.е. ![]() .
.
Итак, каждый элемент группы G записывается, и притом единственным образом в виде ![]() .
.
Замечание
Нормальная силовская p-подгруппа P группы G характеристична в G, т.е. инвариантна при действии любого автоморфизма ![]() . Действительно,
. Действительно, ![]() , поэтому
, поэтому ![]() - силовская р-подгруппа, и, стало быть,
- силовская р-подгруппа, и, стало быть, ![]() , если
, если ![]() . Аналоги силовских подгрупп прослеживаются в алгебраических структурах, далёких от конечных групп.
. Аналоги силовских подгрупп прослеживаются в алгебраических структурах, далёких от конечных групп.
Следствие
Если все делители | G | , кроме 1, после деления на p дают остаток, отличный от единицы, то в G есть единственная силовская p-подгруппа и она является нормальной (и даже характеристической).
Примеры силовских подгрупп.
Пример 1.
Аддитивная группа кольца вычетов ![]() разлагается в прямое произведение своих силовских p-подгрупп, которые являются циклическими подгруппами порядков
разлагается в прямое произведение своих силовских p-подгрупп, которые являются циклическими подгруппами порядков ![]() , если n имеет каноническое разложение n=
, если n имеет каноническое разложение n=![]() .
.
Пример 2.
Силовские p-подгруппы симметрических групп. Как мы знаем, ![]() Каков максимальный показатель e(n), при котором
Каков максимальный показатель e(n), при котором ![]() делит n!? В последовательности 1,2,…,n кратными p будут числа p,2p,…,kp, где
делит n!? В последовательности 1,2,…,n кратными p будут числа p,2p,…,kp, где ![]() , поэтому
, поэтому ![]() . Так как
. Так как 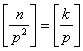 , то
, то 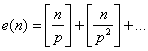 Удобно разложить n по основанию p:
Удобно разложить n по основанию p: ![]() , тогда
, тогда ![]()
Рассмотрим сначала группы ![]() , когда n степень p. Пусть в
, когда n степень p. Пусть в ![]() уже найдена силовская p-подгруппа, т.е. подгруппа
уже найдена силовская p-подгруппа, т.е. подгруппа ![]() порядка
порядка ![]() . Построим по ней в
. Построим по ней в ![]() подгруппу
подгруппу ![]() порядка
порядка ![]() . Для этого разобьём переставляемые символы 1,2,…,
. Для этого разобьём переставляемые символы 1,2,…,![]() на последовательные отрезки длины
на последовательные отрезки длины ![]() . Если
. Если 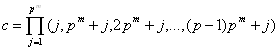 и x – подстановка на символах i-го отрезка, то легко сообразить, что
и x – подстановка на символах i-го отрезка, то легко сообразить, что ![]() - подстановка на символах (i+1)-го отрезка (сложение по модулю p). Отсюда видно, что подгруппа, порождённая подгруппами
- подстановка на символах (i+1)-го отрезка (сложение по модулю p). Отсюда видно, что подгруппа, порождённая подгруппами ![]() , является из прямым произведением, и, стало быть, подгруппа
, является из прямым произведением, и, стало быть, подгруппа ![]() , порожденная подгруппой
, порожденная подгруппой ![]() и элементом с, изоморфна сплетению
и элементом с, изоморфна сплетению ![]() . Подгруппа
. Подгруппа ![]() - искомая, так как
- искомая, так как ![]() .
.
Одновременно мы видим, что силовская p-подгруппа в ![]() изоморфна последовательному сплетению (…(
изоморфна последовательному сплетению (…(![]() циклической группы
циклической группы ![]() с самой собою m раз.
с самой собою m раз.
Теперь пусть n произвольно. Разобьём символы 1,...,n на ![]() одноэлементных,
одноэлементных, ![]() р-элементных и т.д. отрезков. На каждом из этих отрезков рассмотрим симметрическую группу – она будет некоторой степени
р-элементных и т.д. отрезков. На каждом из этих отрезков рассмотрим симметрическую группу – она будет некоторой степени ![]() , а в ней возьмём силовскую p-подгруппу, построенную как выше. Так как эти подгруппы действуют на непересекающихся множествах, то их порождение
, а в ней возьмём силовскую p-подгруппу, построенную как выше. Так как эти подгруппы действуют на непересекающихся множествах, то их порождение ![]() является их прямым произведением, а потому имеет порядок
является их прямым произведением, а потому имеет порядок
![]()
Следовательно, ![]() - силовская p-подгруппа в
- силовская p-подгруппа в ![]() . Из построения видно, что она изоморфна прямому произведению нескольких последовательных сплетений типа (…(
. Из построения видно, что она изоморфна прямому произведению нескольких последовательных сплетений типа (…(![]() .
.
Пример 3
Рассмотрим общие линейные группы над конечными полями. Пусть p – простое число, m, n – целые числа ![]() и
и ![]() . Покажем, что
. Покажем, что ![]() - силовская p-подгруппа группы
- силовская p-подгруппа группы ![]() . Посчитаем порядки этих групп.
. Посчитаем порядки этих групп.
Какие n-ки над полем ![]() могут быть первой строкой невырожденной матрицы? Очевидно, любые, кроме нулевой, т. е.
могут быть первой строкой невырожденной матрицы? Очевидно, любые, кроме нулевой, т. е. ![]() штук. Если первая строка выбрана, то в качестве второй строки можно взять любую, не пропорциональную первой; таких строк
штук. Если первая строка выбрана, то в качестве второй строки можно взять любую, не пропорциональную первой; таких строк![]() . Если две первые строки уже выбраны, то в качестве третьей можно взять любую строку, не зависящую линейно от первых двух; это дает
. Если две первые строки уже выбраны, то в качестве третьей можно взять любую строку, не зависящую линейно от первых двух; это дает ![]() возможностей. И так далее. Значит,
возможностей. И так далее. Значит, ![]() .
.
Так как угловые элементы матриц ![]() пробегают независимо друг от друга всё поле, а всего угловых мест
пробегают независимо друг от друга всё поле, а всего угловых мест ![]() , то
, то ![]() . Из сравнения порядков мы видим, что
. Из сравнения порядков мы видим, что ![]() - силовская p-подгруппа группы
- силовская p-подгруппа группы ![]() .
.
Нахождение силовской подгруппы.
Проблема нахождения силовской подгруппы данной группы является важной задачей вычислительной теории групп. Для групп перестановок Уильям Кантор доказал, что силовская p-подгруппа может быть найдена за время, полиномиальное от размера задачи (в данном случае это порядок группы, помноженный на количество порождающих элементов).
ГЛАВА 2.РЕШЕНИЕ ЗАДАЧ С ПРИМЕНЕНИЕМ ТЕОРЕМ СИЛОВА
Задача 1.
Докажем, что группа порядка 350 не может быть простой.
Решение
![]() , значит, силовская 5-подгруппа имеет порядок 25. N5 должно делить 14 и сравнимо с 1 по модулю 5. Этим условиям удовлетворяет только единица. Значит, в G одна силовская 5-подгруппа, а значит, она нормальна, и поэтому G не может быть простой.
, значит, силовская 5-подгруппа имеет порядок 25. N5 должно делить 14 и сравнимо с 1 по модулю 5. Этим условиям удовлетворяет только единица. Значит, в G одна силовская 5-подгруппа, а значит, она нормальна, и поэтому G не может быть простой.
Задача 2
Найти силовские р-подгруппы в группе всех матриц ![]() с определителем 1 над полем
с определителем 1 над полем ![]() из р элементов.
из р элементов.
Решение.
Пусть ![]() - группа
- группа ![]() с определителем 1 над полем
с определителем 1 над полем ![]() из р элементов. Из разложения
из р элементов. Из разложения
![]()
полной линейной группы ![]() в смежные классы по
в смежные классы по ![]() следует, что
следует, что
![]() (1)
(1)
Рассматривая ![]() как группу автоморфизмов двумерного векторного пространства V над
как группу автоморфизмов двумерного векторного пространства V над ![]() , легко найти порядок
, легко найти порядок ![]() . Действительно,
. Действительно, ![]() действует на множестве пар
действует на множестве пар ![]() базисных векторов. Образом
базисных векторов. Образом ![]() может быть любой отличный от нуля вектор
может быть любой отличный от нуля вектор ![]() (их всего
(их всего ![]() штук), а при всяком выборе
штук), а при всяком выборе ![]() образом
образом ![]() может быть любой вектор
может быть любой вектор ![]() из
из ![]() (таких векторов имеется
(таких векторов имеется ![]() штук). Стало быть,
штук). Стало быть, ![]() , что в сочетании с (1) приводит к формуле
, что в сочетании с (1) приводит к формуле
![]()
По крайней мере две силовские р-подгруппы группы ![]() мы находим сразу:
мы находим сразу:
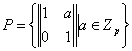 ,
, 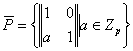 .
.
В соответствии с теоремой 3 имеем ![]()
а так как
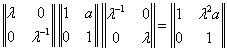
и, следовательно, нормализатор ![]() содержит подгруппу
содержит подгруппу
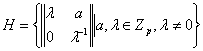
порядка p(p-1), то остаётся единственная возможность
![]() .
.
Между группой
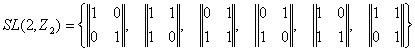
и симметрической группой ![]() непосредственно устанавливается изоморфизм
непосредственно устанавливается изоморфизм
![]()
(обе группы имеют одинаковое задание образующими и соотношениями). При p>2 группа ![]() имеет центр
имеет центр ![]() порядка 2. Фактор- группа
порядка 2. Фактор- группа ![]() , которую естественно называть проективной специальной группой(она является группой преобразований проективной прямой
, которую естественно называть проективной специальной группой(она является группой преобразований проективной прямой ![]() ) , играет важную роль в алгебре со времён Галуа. Дело в том, что при p>3 группа
) , играет важную роль в алгебре со времён Галуа. Дело в том, что при p>3 группа ![]() простая, и это, наряду с
простая, и это, наряду с ![]() ,- один из самых ранних примеров конечных простых групп.
,- один из самых ранних примеров конечных простых групп.
Задача 3
Описать с помощью теоремы Силова все возможные типы групп порядка pq.
Решение
Пусть р, q — простые числа, р < q. Какой должна быть группа G порядка pq? Силовские р- и д-подгруппы из G, будучи подгруппами простого порядка, являются циклическими. Пусть (а), (b) — соответственно силовские р- и q-подгруппа. По теореме Силова число силовских q-подгрупп в G имеет вид 1+kq и делит pq, поэтому силовская q-подгруппа (b) единственна. В частности, она нормальна в G. Число силовских р-подгрупп имеет вид 1+кр и делит q, поэтому возможны два случая:
а) Силовская р-подгруппа (а) единственна. Тогда она нормальна и, значит,![]() . Так как
. Так как ![]() , то
, то ![]() . Таким образом, в этом случае
. Таким образом, в этом случае ![]() .
.
б) Имеется q силовских р-подгрупп. Конечно, это возможно лишь при условии ![]() . Пусть
. Пусть ![]() . Если r=1, то снова
. Если r=1, то снова ![]() ,т. е.
,т. е. ![]() . Пусть
. Пусть ![]() . Индукцией по х получаем
. Индукцией по х получаем ![]() , откуда
, откуда ![]() для всех целых х, у. При х=р, у=1 это дает
для всех целых х, у. При х=р, у=1 это дает ![]() , кроме того, получаем формулу умножения
, кроме того, получаем формулу умножения ![]() .
.
Обратно, легко проверить, что если ![]() ,
, ![]() ,
, ![]() , то эта формула умножения определяет неабелеву группу порядка pq. Наконец, решения сравнения
, то эта формула умножения определяет неабелеву группу порядка pq. Наконец, решения сравнения ![]() составляют циклическую группу порядка р, поэтому те из них, которые
составляют циклическую группу порядка р, поэтому те из них, которые![]() , имеют вид
, имеют вид ![]() , где r — одно из них. Все эти решения определяют одну и ту же группу, так как замена порождающего а на
, где r — одно из них. Все эти решения определяют одну и ту же группу, так как замена порождающего а на ![]() приводит к замене r на
приводит к замене r на ![]() .
.
Таким образом, с помощью теоремы Силова мы описали все возможные типы групп порядка pq; их оказалось два — абелев и неабелев, причем второй существует только при условии ![]() .
.
ЗАКЛЮЧЕНИЕ
При изучении абелевых групп видно, что их строение во многом определяется строением максимальных р-подгрупп. В теории конечных групп максимальные р-подгруппы также играют существенную роль. В этом курсовой были доказаны теоремы Силова о конечных группах: для каждой степени ![]() , делящей порядок группы, существует подгруппа порядка
, делящей порядок группы, существует подгруппа порядка ![]() , причем если
, причем если ![]() делит порядок группы, то всякая подгруппа порядка
делит порядок группы, то всякая подгруппа порядка ![]() содержится в некоторой подгруппе порядка
содержится в некоторой подгруппе порядка ![]() ; все максимальные р-подгруппы попарно сопряжены в группе, а их число сравнимо с 1 по модулю р. Эта теорема была доказана норвежским математиком Л. Силовом в 1872 году. В связи с этой теоремой и в честь ее автора максимальные р-подгруппы конечных (а часто и бесконечных) групп называются силовскими р-подгруппами.
; все максимальные р-подгруппы попарно сопряжены в группе, а их число сравнимо с 1 по модулю р. Эта теорема была доказана норвежским математиком Л. Силовом в 1872 году. В связи с этой теоремой и в честь ее автора максимальные р-подгруппы конечных (а часто и бесконечных) групп называются силовскими р-подгруппами.
Из теоремы Силова вытекает, в частности, что силовские р-подгруппы конечной группы — это в точности подгруппы порядка ![]() , где
, где ![]() — максимальная степень р, делящая порядок группы. Отметим, что если число m делит порядок конечной группы G, но не является степенью простого числа, то в G может и не быть подгрупп порядка m — например, в знакопеременной группе А4 порядка 12 нет подгрупп порядка 6.
— максимальная степень р, делящая порядок группы. Отметим, что если число m делит порядок конечной группы G, но не является степенью простого числа, то в G может и не быть подгрупп порядка m — например, в знакопеременной группе А4 порядка 12 нет подгрупп порядка 6.
В теории групп теоремы Си́лова представляют собой неполный вариант обратной теоремы к теореме Лагранжа и для некоторых делителей порядка группы G гарантируют существование подгрупп такого порядка.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. А. И. Кострикин. Введение в алгебру, III часть. М.: Физматлит, 2001.
2. Э. Б. Винберг. Курс алгебры. М.: Факториал-Пресс, 2002.
3. М.И. Каргаполов, Ю.И. Мерзляков. Основы теории групп. М.:Наука, 1982.