Теория вероятностей и математическая статистика
Элементы комбинаторики
При решении вероятностных задач часто приходится в заданном множестве выбирать подмножества, обладающие определенными свойствами. Поскольку в таких задачах речь идет про те или иные комбинации объектов, то их называют комбинаторными задачами.
Множество наз. Упорядоченным, если в нем указан порядок следования элементов. Например ![]()
Основные правила комбинаторики
1.Правило суммы
Пусть из множества А элемент а1 можно выбрать n1 способами, элемент а1-n1 способами, а2-n2 способами,…, аk-nk спосбами. Тогда выбор одного из этих элементов или а1, или а2,…, или аk можно произвести n1+n2+…+nk способами.
2.Правило произведения
Пусть из множества А элемент а1 можно выбрать n1 способами, элемент а1-n1 способами, а2-n2 способами,…, аk-nk спосбами. Тогда одновременный выбор элементов а1,а2,…,аk можно выбрать n1*n2*…*nk способами.
Пример
Из 3-ех классов спорт. школы нужно составить команду для соревнований, взяв по одному ученику из класса. Сколько команд можно составить, если в одном классе 18 учеников, в другом-20, в третьем-22.
Решение:n1=18, n2-20, n3=22
n1*n2*n3=18*20*22=7820 способов.
Основные соединения комбинаторики.
1)Размещения
Пусть множество А состоит из n элементов. Будем выбирать из оттого множества упорядоченные множества, состоящие из k элементов. Такие подмножества будут называться размещениями из nэлементов по k. Размещения отличаются друг от друга как элементами, так и порядком.
Например , из множества ![]() составим размещения по 2 элемента.
составим размещения по 2 элемента. ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
Число размещений из n элементов по k обозначают ![]() и вычисляют по формуле:
и вычисляют по формуле: ![]() ; (0!=1)
; (0!=1)
2)Перестановки из nэлементов k
Перестановками из nэлементов по k называют размещения, у которых n=k. Перестановки отличаются только порядком элементов. ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;![]() ;
; ![]()
Число перестановок из n элементов по k (n=k):
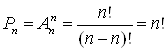
3)Сочетания из nэлементов по k
Пусть мн-во А состоит из n элементов. Из него будем выбирать неупорядоченные подмножества, содержащие k элементов, которые будут называться сочетаниями из nэлементов k. Сочетания различаются между собой только элементами. ![]() :
: ![]() ,
,![]() ,
,![]()
Число сочетаний из n элементов по k:
![]()
Примеры:
1)Студентам нужно сдать сдать 4-ре экзамена за 8 дней. Сколькими способами можно составить расписание?
(2,3,7,8) Из множества, содержащего 8 элементов выбираем подмножества по 4 элемента, порядок которых нам не безразличен, следовательно число способов:
![]()
2)На 4-ех карточках написаны цифры 0,1,2,3. Сколько различных четырехзначных чисел чисел можно составить из этих карточек?
4!-3!=24-6=18
3)В хоккейном турнире участвует 6 команд. Каждая команда должна сыграть с каждой одну игру. Сколько игр будет сыграно в турнире?
Т.к в выбираемых множествах по 2 элемента из 6, порядок безразличен, то кол-во игр=числу сочетаний из 6 по 2:
![]()
4)6 друзей собрались на встречу. Один из них произнес тост: собираться столько лет пока каждый не посидит на новом месте. ![]()
Испытания и события. Виды событий
В любой точной науке существуют основные понятия. Если в геометрии это: точка, прямая, плоскость, то в теории вероятности основными понятиями являются испытания, события, вероятность.
Испытание(опыт)-осуществление какого-либо комплекса условий.
Испытанием будет являться бросание игральной кости.
Событие(исход)-результат испытания.
События могут быть достоверными, невозможными, случайными.
Достоверное событие-событие, кот. обязательно произойдет в результате данного испытания. ![]() . Например, при бросании игральной кости выпало число от 1 до 6.
. Например, при бросании игральной кости выпало число от 1 до 6.
Невозможное событие-событие, кот. не может произойти в результате данного испытания. Например, , при бросании
игральной кости выпало 7 очков.
Случайное событие-событие, кот. может произойти, а может не произойти в результате данного испытания. А,В,С,… Например, выпало 6 очков при бросании кости.
Виды случайных событий
Случайные события называются совместными, если появление одного из них не исключает появление другого. В противном случае - несовместние.
А - в аудиторию вошел мужчина, В - в аудиторию вошел человек старше 30 лет. А и В - совместные
Стрелок произвел выстрел по цели. А - попадание, В - промах; А и В - несовместные.
Случайное событие называется единственно возможным, если в результате испытания появление одного и только одного из них является достоверным событием. Бросают монету. А - герб, В - надпись.
Случайные события называются равновозможными, если в результате испытания нет оснований считать, что одно из них более возможно, чем другое.
Случайные события называются противоположными, если не появление одного из них влечет появление другого. А, ![]()
Совокупность всех единственно возможных событий данного испытания составляет полную группу событий
А1-1 очко
А2-2 очка
А3-3 очка
А4-4 очка Полная группа событий
А5-5 очков
А6-6 очков
Действия над событиями
1)Суммой двух событий А и В называется событие, состоящее в том,
что произошло или событие А, или событие В, или оба вместе, т.е.
произошло хотя бы одно событие. С=А+В “+”-или
Примеры:
1)Соб. А-турист посетил город А
Соб. В-турист посетил город В
Соб. С-турист посетил город С
А+В=С – турист посетил или г. А, или г.В, или оба вместе.
2)При бросании игральной кости:
А-выпало четное число очков ![]()
В-выпало число очков, кратное 3-ем ![]()
А+В-выпало число очков или четное, или кратное 3-ем ![]()
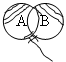
Геометрическая интерпретация суммы событий
Диаграмма Венна
1 ![]()
![]()
![]()
![]()
![]()
![]() Для совместных
Для совместных
![]() событий
событий
2 ![]()
![]()
![]() Для несовмест. соб.
Для несовмест. соб.
Произвольным образом бросаем точку на плоскость. Если она попадет в область А, то произошло событие А, если в область В, то-событие В, если попадет в область с двухсторонней штриховкой, то события А и В произошли одновременно. Тогда сумме событий будет соответствовать область, отмеченная жирной линией. В случае несовместных событий сумме А+В будет соответствовать две непересекающиеся области. 2)Произведением событий А и В называется событие С, которое наступает с совместным наступлением А и В. А*В “ * ”-заменяет союз « И »
![]()
![]()
![]()
![]()
![]()
![]() Для произведения соб.
Для произведения соб.
![]() Аналогично определяются сумма и произведение для нескольких событий.
Аналогично определяются сумма и произведение для нескольких событий.
Классическая формула вероятности. Свойства вероятности.
Вероятность является одним из основных понятий в теории вероятностей.
При употреблении этого слова мы интуитивно оцениваем возможность появления того или иного события. Можно сказать, что одно событие наступит чаще, чем другое.
В урне содержится 28 шаров, из них 2 белых, 13 красных, 13 черных. На удачу вынимаем 1 шар. Красный или черный шар можно вытянуть с большей возможностью, а белый – с меньшей. Из этого примера видно, что каждое событие обладает определенной степенью возможности , т.е. некоторой числовой оценкой.
Вероятностью события А называется численная мера объективной возможности его появления. Р=Р(А)
Классической схемой или схемой случаев называется испытание, при котором число исходов (событий) конечно и все из них равновозможные.
Исход испытания (события) называется благоприятствующим событию А, если его появление влечет наступление события А.
Классической вероятностью события А называется отношение числа исходов М, благоприятствующих событию А , к общему числу всех исходов испытания N. Р(А)=M/N
Из определения следуют следующие свойства.
1)Вероятность достоверного события. Р(![]() )=1
)=1
![]()
![]() 2)Вероятность невозможного события. Р=0
2)Вероятность невозможного события. Р=0
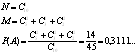
3) Вероятность случайного события. 0 4) Вероятность любого события . 5)Сумма вероятностей противоположных событий =1. Р(А)+Р(Ä)=1 6)Сумма вероятностей полной группы событий=1. Примеры: 1)Консультационный пункт института получает пакеты с контрольными из городов А,В,С. Вероятность получения пакета из г. А 0,7, из В 0,2. Найти вероятность получения пакета из г. С В-пакет получен из г. В Полная группа событий Р(А)+Р(В)+Р(С)=1 0,7+0,2+Р(С)=1 ; Р(С)=0,1 2)Брошено 2 игральные кости. Найти вероятность того, что 6 очков появится хотя бы на одной грани. Событие А – 6 очков появилось хотя бы на одной грани Событие Р(А)=1 - Р( Р( N=6*6=36 M=5*5=25 Р( Р(А)=1 - Р( 3)На 5 карточках написаны буквы «а, д ,к, л, о». Карточки тщательно перемешивают, а затем выкладывают по одной на стол. Какова вероятность того, что получится слово «лодка»? Событие А – получилось слово «лодка» Р=M/N Р(А)=1/120 5)Набирая номер телефона абонент забыл 3 последние цифры и помня, что они разные набрал, номер телефона. Какова вероятность того, что номер набран верно? Р(А)=М/N М=1 Р(А)=1/720 6)В ящике имеется 10 деталей, среди них 7 стандартных. На удачу берем 6. Какова вероятность того, что среди 6 деталей окажется ровно 4 стандартных? Соб. А – среди 6 выбранных деталей 4 стандартные. Р(А)=M/N 7)В ящике лежит 10 заклепок, изготовленных из разного материала: 5 железных, 3 латунных, 2 медных. Наудачу берем 2 заклепки. Какова вероятность того, что они окажутся сделанными из одного материала? Соб. А – вытащенные заклепки из одного материала. Р(А)=M/N Статистическая и геометрическая вероятность 1) Статистическая вероятность. Классическая формула вероятности дает непосредственно вычислять вероятность, но она предполагает выполнение некоторых условий. Она относится к событиям, обладающих симметрией и образующих полную группу событий. Многие группы событий не подходят под классическую схему, но каждое событие такой группы обладает некоторой возможностью наступления. Например, если игральная кость изготовлена из неоднородного материала, то вероятность появления некоторого числа очков не равна 1/6. Иногда не удается выделить полную группу событий. Известно много случаев, когда результаты являются непредсказуемыми, хотя изначально все исходы были учтены. В подобных случаях находят относительную частоту события А m-число опытов, в результате которых произошло событие А. Оказывается, что при Результаты опытов при бросании монеты. n – число испытаний m – число, соответствующее выпадению герба 2) Геометрическая вероятность N=D ; M=d Найти вероятность того, что точка, брошенная в треугольник попадет в круг. Вероятность появления хотя бы одного события. Задачу из пункта Вероятность суммы событий (Вероятность попадания в цель при стрельбе из трех орудий: Р1=0,8; Р2=0,7; Р3=0,9. Найти вероятность того, что цель будет поражена.) Можно решить намного быстрее, если применить теорему о вероятности хотя бы одного события. Пусть в результате опыта может появиться n независимых в совокупности событий,вероятности которых известны. Теорема. Вероятность появления хотя бы одного из n независимых событий А1, А2, …,Аn равна разности между единицей и произведением вероятностей противоположных событий, т.е. Р(хотя бы одного события)=1-q1*q2*…*qn Если р1=р2=…рn, то Р(хотя бы одн. соб.)= Вопрос №33. Вероятность произведения событий. Два события называются зависимыми, если вероятность одного из них зависит от появления или не появления другого. В противном случае события называются независимыми. 7 белых 1) Событие А – появился 3 черных белый шар. Р(А)=0,7 шаров Событие В – появился черный шар. Р(В)=1/3 А и В – зависимые Р(В) – условная вероятность 2)А-появился белый шар.Р(А)=0,7 (с возвратом) В – появился черный шар. Р(В)=0,3 В данном случае События А1, А2,…, Аn называются независимыми в совокупности, если каждое из них не зависит от произведения остальных событий и от каждого в отдельности. Из попарной независимости не следует независимость в совокупности. Если событие А1, А2,…, Аn – независимы, то Теорема Вероятность совместного появления двух зависимых событий = произведению вероятности одного из них на условную вероятность другого. В урне 7 белых, 3 черных шара. На удачу один за другим выбираем по одному шару без возврата. Найти вероятность того, что первый шар оказался белым, а второй черным. Теорема Вероятность совместного появления двух независимых событий = произведению вероятностей этих событий. Вероятность появления только одного события Пусть даны три независимых события А1, А2, А3; р1, р2, р3 – их вероятности. Найдем вероятность появления только одного из них. B1=(только А1)=А1* B2=(только А2)= B3=(только А2)= Т.к. В1, В2, В3 – несовместные, то Р(только одного события)=Р(В1)+Р(В2)+Р(В3) Т.к. А1, А2, А3 – независимые, то Ä1, Ä2, Ä3 тоже независимые. Р( Р(только одного соб.)=p1*q2*q3+q1*p2*q3+q1*q2*p3 Вероятность попадания в цель при стрельбе из трех орудий: Р1=0,7 Р2=0,8; Р3=0,9. Найти вероятность того, что только одно орудие поразило цель.Р1=0,8; Р2=0,7; Р3=0,9; q1=0,2; q2=0,3; q3= 0,1 Р(только одного события)= 0,7*0,2*0,1+0,3*0,8*0,1+0,3*0,2*0,9=0,092 Наивероятнейшее число появления события А в независимых испытаниях Пусть производится n независимых испытаний. где р – вероятность появления события А при одном испытании, q – вероятность не появления события А при одном испытании. Число k при котором данная вероятность окажется большей будет называться наивероятнейшим числом появления события А. Если: 1) (n*p-q) – дробное число, существует одно наивероятнейшее число Задача. 1) n=15; p=0,9; q=0,1 Вероятность суммы событий Теорема. Вероятность появления одного из двух несовместных событий = сумме вероятностей этих событий. Доказательство: N – число всевозможных исходов испытания М1 – число исходов, благоприятствующих событию А; М2 – число исходов, благоприятствующих событию В. Т.к. события несовместные, то в них не будет общих благоприятствующих исходов. Соб. А – попадание в обл. А А В Соб. В – попадание в обл. В Теорема. Вероятность появления одного из двух совместных событий или обоих вместе = суммевероятностей этих событий без вероятности их совместного появления. Докажем с помощью диаграммы Венна. Представим (А+В) и В через сумму двух несовместных событий. A+B=A+B* B=A*B+B* А А A+B=A+B-A*B ![]()
![]()
![]()
![]() А-пакет получен из г. А
А-пакет получен из г. А![]() С -пакет получен из г. С
С -пакет получен из г. С ![]() – появилось число очков не равное 6
– появилось число очков не равное 6![]() )
)![]() )=М/N
)=М/N![]() )=25/36
)=25/36![]() )=1-25/36=11/36
)=1-25/36=11/36![]()

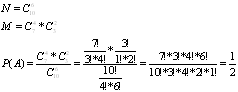
![]() ; n-число произведенных опытов
; n-число произведенных опытов![]() относительная частота неограниченно близко приближается к определенному постоянному числу. Это число и будет называться статистической вероятностью.
относительная частота неограниченно близко приближается к определенному постоянному числу. Это число и будет называться статистической вероятностью.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1,
1, ![]() 2,…,
2,…, ![]() n.
n.![]()
![]() Произведем 2 испытания.
Произведем 2 испытания.![]()
![]()
![]() 1,
1, ![]() 2,…,
2,…, ![]() n – независимы.
n – независимы.![]()
![]()
![]()
![]() 2*
2* ![]() 3
3![]() 1* А2*
1* А2* ![]() 3
3![]() 1*
1* ![]() 2* А3
2* А3![]() 1)=q1; P(
1)=q1; P(![]() 2)=q2; P(
2)=q2; P(![]() 3)=q3
3)=q3![]() ,
, ![]()
![]() ; 2) (n*p-q) – целое число, то существуют два наивероятнейших числа
; 2) (n*p-q) – целое число, то существуют два наивероятнейших числа ![]() и
и ![]() ; 3) n*p – целое, то наивероятнейшее число
; 3) n*p – целое, то наивероятнейшее число ![]() .
.![]() 2) n=24; p=0,6; q=0,4
2) n=24; p=0,6; q=0,4![]() 3) n=25; p=0,08; q=0,92
3) n=25; p=0,08; q=0,92![]()
![]()
![]() Мишень разделили на две области. Найти вероятность того, что стрелок попал в мишень.
Мишень разделили на две области. Найти вероятность того, что стрелок попал в мишень.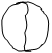
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Аналогично с помощью диаграммы Венна можно доказать вероятность суммы трех совместных событий.
![]() Вероятность попадания в цель при стрельбе из
Вероятность попадания в цель при стрельбе из
трех орудий: Р1=0,8; Р2=0,7; Р3=0,9. Найти вероятность того, что цель будет поражена.
Событие А – цель поражена. Т.к. события совместные, то :
Р(А)=0,8+0,7+0,9-0,8*0,7-0,9*0,8-0,7*0,9+0,8*0,7*0,9=0,994
Формула полной вероятности
Событие А может произойти при условии появления одного из несовместных событий Н1, Н2,…, Нn, образующих полную группу событий. Их называют гипотезы.
Гипотезы исчерпывают все возможные предположения первого этапа опыта, а событие А это один из возможных исходов испытания второго этапа опыта.
Пусть известны вероятности гипотез: Р(Н1), Р(Н2), Р(Н3), …, Р(Нn) и условные вероятности события А:
![]()
Вероятность события А = сумме произведения вероятностей гипотез на соответствующие им условные вероятности.

Это Формула полной вероятности.
Задача. В двух ящиках содержится по 20 деталей, причем в первом 17 стандартных, а во втором 15 стандартных. Из второго ящика на удачу берется одна деталь и перекладывается в первый. Найти вероятность того, что извлеченная из первого ящика деталь окажется стандартной.
Гипотезы: Н1 – переложена стандартная деталь
Н2 – переложена нестандартная деталь
Р(Н1)=15/20
Р(Н2)=5/20
Событие А – из первого ящика извлекается стандартная деталь
![]()

Формулы Бейеса (вероятности гипотез)
Пусть событие А может произойти при условии появления одного из несовместных событий Н1, Н2, Н3,…,Нn, называемых гипотезами.
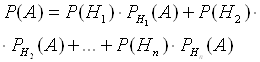
По этой формуле можно найти вероятность события А до проведении опыта.
Если событие А уже наступило (после проведения опыта) поставим задачу определить как при этом изменяются вероятности гипотез.
Найдем ![]() .
.

Аналогично можно получить формулы из остальных гипотез.
На 3-ех дочерей Алису, Бетти и Шарлоту в семье возложена обязанность мыть тарелки. Поскольку Алиса старшая ей приходится выполнять 40 % работы. Остальные 60 % делят между собой Бетти и Шарлота. Когда Алиса моет тарелку, вероятность для нее разбить тарелку 0,02, для Бетти 0,02, для Шарлоты 0,03. Родители не знают, кто вечером мыл посуду, но слышали звон разбитой тарелки. Какова вероятность того, что посуду мыла а) Алиса, б) Бетти, в) Шарлота.
Событие А – тарелка разбита.
Гипотезы: Н1 – мыла Алиса; Н2 – мыла Бетти
Н3 – мыла Шарлота
Р(Н1)=0,4; Р(Н2)=0,3; Р(Н3)=0,3
![]() Т.к. событие А уже произошло, то необходимо применить вероятности гипотез.
Т.к. событие А уже произошло, то необходимо применить вероятности гипотез.


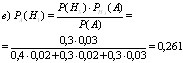
Вывод: формула Бейеса позволяет переоценить вероятности гипотез после того, как становится известным результат испытания, в результате которого появилось событие А. Отличие формулы полной вероятности от формулы Бейеса: формула полной вероятности применяется до опыта, а формула Бейеса после опыта.
Предельные теоремы в схеме Бернулли
![]()
Если n и k довольно большие
![]() , то в таких случаях для вычисления вероятностей применяют предельные теоремы.
, то в таких случаях для вычисления вероятностей применяют предельные теоремы.
Теорема Пуассона.
Если число испытаний n неограниченно увеличивается, т.е. ![]() и вероятность Р наступления события А в одном испытании уменьшается, т.е.
и вероятность Р наступления события А в одном испытании уменьшается, т.е. ![]() , но при этом число
, но при этом число ![]() , то вероятность того, что событие n наступит ровно k раз:
, то вероятность того, что событие n наступит ровно k раз:
![]() - асимптотическая формула Пуассона. Ее обычно используют, когда
- асимптотическая формула Пуассона. Ее обычно используют, когда ![]()
Некоторые электронные устройства выходят из строя, если откажет определенная микросхема. Вероятность ее отказа в течение одного часа работы устройства = 0,004. Какова вероятность того, что за 1000 часов работы придется 5 раз менять микросхему.
n=1000; p=0,004; ![]()
![]()
Если число n достаточно большое, а вероятность
Не стремится к 0, то для вычисления вероятность используются предельные формулы Муавра – Лапласа.
Интегральная теорема Муавра – Лапласа
Если вероятность Р наступления события А при независимых испытаниях постоянна и отлична от 0 и 1, то вероятность того, что при n независимых испытаниях событии А появится не менее k1 и не более k2 раз может быть найдена по приближенной формуле:
![]()
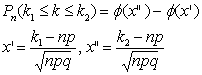
ф – функция Лапласа, значения в таблице
ф(-х)=-ф(х)
![]()
Задача.
Вероятность выпуска нестандартной лампы 0,1. Чему равна вероятность того, что в партии из 2000 ламп число стандартных не менее 1790?
p=0,9; n=2000; k1=1790; k2=2000
![]()

![]()
Среднее квадратическое отклонение дискретной случайной величины
Эта характеристика также как и дисперсия определяет рассеяние случайной величины Х вокруг ее математического ожидания. Дисперсия имеет размерность несовпадающую со значением случайной величины Х, а среднее квадратическое отклонение имеет размерность, совпадающую со значением случайной величины.

Теорема. Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин = корню квадратному из суммы квадратов средних квадратических отклонений этих величин.
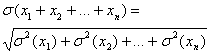
Доказательство:

![]() Дифференциальная функция распределения случайной величины. Свойства
Дифференциальная функция распределения случайной величины. Свойства
![]() - плотность распределения вероятностей. Дифференциальная функция распределения существует только у непрерывной случайной величины.
- плотность распределения вероятностей. Дифференциальная функция распределения существует только у непрерывной случайной величины.
![]()
0 при ![]()
F(X) = k*X при ![]()
1 при ![]()
![]()
0 при ![]()
f(X) = k при ![]()
1 при ![]()
![]()
![]() F f(X)
F f(X)
Чтобы найти вероятность попадания случайной величины в интервал (a; b) с помощью дифференциальной функции используют функцию
![]()
Чтобы найти интегральную функцию распределения случайной величины используют:
![]()
Свойства.
1) ![]()
2) 
комбинаторика случайная величина вероятность математический
Математическое ожидание дискретной случайной величины. Свойства.
Математическое ожидание (среднее значение ДСВ) – постоянное число, равное сумме произведений значений случайных величин на их соответствующие вероятности.
![]()
Таблица
| Х | 2 | 3 | 5 |
| Р | 0,3 | 0,4 | 0,3 |
М(Х)=2*0,3+3*0,4+5*0,3=3,3
Свойства.
1) М(С)=С
2) М(СХ)=С*М(Х)
| Х | х1 | х2 | … | х3 |
| Р | Р1 | Р2 | … | Р3 |
![]()
| С*Х | С*х1 | С*х2 | … | С*х3 |
| Р | Р1 | Р2 | … | Р3 |
![]()
![]() 3) М(Х+У)=М(Х)+М(У) если Х и У -
3) М(Х+У)=М(Х)+М(У) если Х и У -
4) М(Х-У)=М(Х)-М(У) независимые
5) М(Х*У)=М(Х)*М(У) случ. Величины
Пример. Найти математическое ожидание М(Х+У) двумя способами.
1. Х+У; М(Х+У)
2. М(Х)+М(У)
6) М(Х-М(Х))=0
(Х-М(Х)) – отклонение случайной величины от ее математического
Действия над дискретными случайными величинами
ДСВ можно 1) умножать на число,
2) возводить в степень.
1) умножение на число
2) возведение в степень
Две ДСВ называются независимыми, если событие Аi, состоящее в том, что случайная величина Х примет значения ![]() ,
, ![]() и
и
событие![]() будут независимыми. В противном случае ДСВ называются зависимыми.
будут независимыми. В противном случае ДСВ называются зависимыми.
Несколько ДСВ называются взаимно независимыми, если закон распределения одной из них не зависит от того, какие ранее возможные значения приняли остальные величины.
Пример.
![]()
![]()
Если в верхней строке таблицы появляются одинаковые значения, то соответствующие столбцы объединяем и их вероятности складываем.
Действие вычитания и умножения выполняются аналогично.
Случайные величины
Дискретные случайные величины.
1) Случайной величиной называют величину, которая в результате испытания примет одно и только одно значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены. Случайные величины могут быть:
дискретные (прерывные), которые принимают лишь изолированные значения с определенными вероятностями. Их число может быть конечным и бесконечным (счетное). Пример: среди 100 новорож-денных число родившихся мальчиков от 1 до 10.
Непрерывные, которые могут принимать все значения из некоторого конечного промежутка. Пример: множество чисел принадлежащих промежутку![]()
Дискретные случайные величины. Обозначаются заглавными буквами латинского алфавита X, Y,…, а их возможные значения х1, х2,…, хn.
Закон распределения ДСВ – Это соответствие между возможными значениями и их вероятностями. Его можно задать аналитически, таблично и графически, чаще всего задают таблицей:
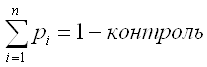
Задача. В денежно-вещевой лотерее выпущено 110 билетов. Разыгрывается приз 50000 рублей и 10 призов по 1000 рублей. Найти закон распределения случайной величины Х – стоимость выигрыша для владельца одного билета.
| Х | 500000 | 1000 | 0 |
| Р | 1/110 | 10/110 | 99/110 |
Дисперсия (рассеянное значение случайной величины вокруг математического ожидания этой величины)
Дисперсия – математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
1) ![]()
2) 
Пример.
| Х | 1 | 2 | 5 |
| Р | 0,3 | 0,5 | 0,2 |
М(Х)=1*0,3+2*0,5+5*0,2+5*0,2=2,3
![]()
![]()