Расчет максимального значения восстанавливающей силы
Сибирский государственный университет путей сообщения
Домашнее задание по дисциплине «Математическое моделирование»
Задачи №1, №2
Разработал: студент гр. М-511
Ревнивцев
2008
Задача№1
В тупике железнодорожного пути установлен буфер (рисунок 1), имеющий упругий элемент с нелинейной жесткостью, восстанавливающая сила которого изменяется по закону
![]() .
.
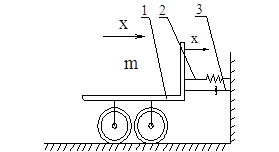
1 – вагон; 2 – буфер; 3 – демпфер
Рисунок 1 – Схема к решения задачи.
В направлении тупика движется вагон массой m и скоростью X. При столкновении вагона с упругим элементом, последний смещается на величину X1. В задаче также приняты следующие допущения: 1) масса буфера мала по сравнению с массой вагона; 2) после удара контакт между этими объектами сохраняется.
Восстанавливающая сила (закон изменения):
![]() (1)
(1)
В задаче требуется определить:
- максимальное перемещение буфера;
- максимальное значение восстанавливающей силы;
- время, за которое восстанавливающая сила достигнет максимального значения.
На данную систему (рисунок 1) действуют силы: сила инерции движущегося вагона; сила демпфирования (или сила вязкого трения), пропорциональная скорости движения вагона; а также восстанавливающая сила упругого элемента-демпфера.
Сила инерции:
![]() , (2)
, (2)
Сила демпфирования:
![]() , (3)
, (3)
Сила упругости:
![]() (4)
(4)
Для решения поставленной задачи следует решить обыкновенное дифференциальное уравнение второго порядка вида:
![]() (5)
(5)
Заменим уравнение (5) системой уравнений первого порядка, для этого введем новую неизвестную функцию ![]() и перепишем исходное уравнение, представив его в виде системы из двух уравнений:
и перепишем исходное уравнение, представив его в виде системы из двух уравнений:
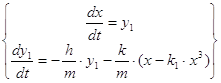 (6)
(6)
Решение проводим в системе MathCad с построением графических зависимостей: 1) скорости движения вагона от времени; 2) перемещения буфера от времени; 3) восстанавливающей силы от времени. Неизвестные выше исходные данные записываются непосредственно в программе.
Исходное уравнение имеет вид:
![]() , (7)
, (7)
где ![]() - коэффициент демпфирования,
- коэффициент демпфирования, ![]() ;
;
![]() - масса вагона, кг;
- масса вагона, кг;
![]() - жесткость упругого элемента, Н/м;
- жесткость упругого элемента, Н/м;
![]() - численный коэффициент,
- численный коэффициент, ![]() ;
;
![]() - скорость вагона при подходе к тупику, м/с;
- скорость вагона при подходе к тупику, м/с;
Начальные условия:
![]()
![]()
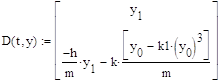 (8)
(8)
Уравнение (8) решается в системе MathCad посредствам встроенной функцией – rkfixed:
Z:= rkfixed (y, 0, t, n. D) (9)
где Z – вектор неизвестных;
y – вектор начальных условий;
0 и t – интервал, на котором ищется решение;
n – количество точек на интервале.
|
Подобные работы: