Область прогноза для однофакторной и двухфакторной модели. Точечный прогноз на основании линейной прогрессии
Министерство образования и науки Украины
Донбасская государственная машиностроительная академия
Контрольная работа
по дисциплине: «Эконометрика»
Выполнил:
студент гр. ПВ 09-1з
Измайлов А.О.
Проверила:
Гетьман И.
Краматорск 2010
1. Теоретический вопрос
Область прогноза для однофакторной и двухфакторной модели. Точечный прогноз на основании линейной прогрессии.
Область прогнозов находится так: среди выборочных х находят xmin и xmax. Отрезок прямой, заключенный между ними называется областью прогнозов.
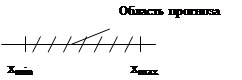 |
Прогнозируемый доверительный интервал для любого х такой ![]() .
.
Совокупность доверительных интервалов для всех х из области прогнозов образует доверительную область, которая представляет область заключения между двумя гиперболами. Наиболее узкое место в точке ![]() .
.
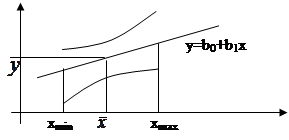 |
Прогноз для произвольного х дает интервал, в который с вероятностью g попадает неизвестное ![]() . Т.е. прогноз при заданном х составит от
. Т.е. прогноз при заданном х составит от ![]() до
до ![]() с гарантией
с гарантией ![]() .
.
Максимальная ошибка прогноза.
Выборочные значения yi равны ![]() , где
, где ![]() коэффициенты регрессии для всей генеральной совокупности,
коэффициенты регрессии для всей генеральной совокупности, ![]() - случайная величина, значение которой мы определить не можем, так как не знаем
- случайная величина, значение которой мы определить не можем, так как не знаем ![]() .
.
Для неизвестных коэффициентов ![]() могут быть найдены доверительные интервалы, в которые с надежностью g попадают
могут быть найдены доверительные интервалы, в которые с надежностью g попадают ![]() :
: ![]() ,
, ![]() .
.
Геометрический смысл коэффициента ![]() - ордината пересечения прямой регрессии с осью 0Y, коэффициента
- ордината пересечения прямой регрессии с осью 0Y, коэффициента ![]() - угловой коэффициент прямой регрессии. Вследствие этого возникает следующая ситуация:
- угловой коэффициент прямой регрессии. Вследствие этого возникает следующая ситуация:
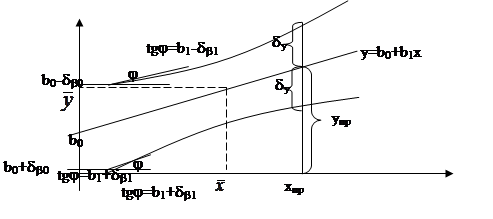
Истинная прямая регрессии может с вероятностью g занимать любое положение в доверительной области.
Наиболее максимальное отклонение от расчетного значения - ![]() или
или ![]() . Найдем ошибку прогноза для каждого из значений:
. Найдем ошибку прогноза для каждого из значений:
![]() ,
, ![]() .
.
Т.е. максимальная ошибка прогноза в процентах составляет: ![]() , т.е. чем больше полуширина доверительного интервала, тем больше ошибка. Ширина доверительного интервала возрастает с ростом коэффициента доверия и уменьшается с ростом объема выборки со скоростью
, т.е. чем больше полуширина доверительного интервала, тем больше ошибка. Ширина доверительного интервала возрастает с ростом коэффициента доверия и уменьшается с ростом объема выборки со скоростью ![]() . Т.е. увеличив объем выборки в 4 раза, в 2 раза сузим доверительный интервал, т.е. в 2 раза уменьшим ошибку прогноза. С уменьшением коэффициента доверия уменьшается ошибка прогноза, но растет вероятность того, что истинное значение не попадет в доверительный интервал.
. Т.е. увеличив объем выборки в 4 раза, в 2 раза сузим доверительный интервал, т.е. в 2 раза уменьшим ошибку прогноза. С уменьшением коэффициента доверия уменьшается ошибка прогноза, но растет вероятность того, что истинное значение не попадет в доверительный интервал.
Прогноз на основании линейной модели для двуфакторной модели.
Целью регрессионного анализа является получение прогноза с доверительным интервалом. Прогноз делается по уравнению регрессии
![]() (1)
(1)
Точка прогноза ![]() из -мерного пространства с координатами
из -мерного пространства с координатами ![]() выбирается из области прогноза. Если, например, модель двухфакторная
выбирается из области прогноза. Если, например, модель двухфакторная ![]() , то область прогноза определяется прямоугольником, представленным на рис. 1.
, то область прогноза определяется прямоугольником, представленным на рис. 1.
 |
Рис. 1
Т.е. область прогноза определяется системой неравенств:
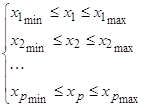
Чтобы получить формулу для вычисления полуширины d доверительного интервала, нужно перейти к матричной форме записи уравнения регрессии.
Матричная запись многофакторной регрессии
Данные для построения уравнения регрессии, сведем в таблицу:
Таблица 1
| № набл | Y | X1 | X2 | … | Xp |
| 1 | y1 | x11 | x12 | x1p | |
| 2 | y2 | x21 | x22 | x2p | |
| … | |||||
| n | yn | xn1 | xn2 | xnp |
![]() (2)
(2)
Подставляя в уравнение (2) значения из каждой строки таблицы, получим уравнений.
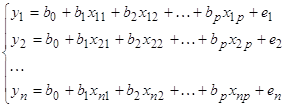 (2)
(2)
ei – случайные отклонения (остатки), наличие которых объясняется тем, что выборочные точки не ложатся в точности на плоскость (1), а случайным образом разбросаны вокруг нее.
![]()
Чтобы записать систему (2) в матричном виде, вводим матрицу X, составленную из множителей при коэффициентах b1, b2, …, bp.
Матрица 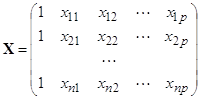 . Размерность матрицы n´p+1.
. Размерность матрицы n´p+1.
Еще вводятся матрицы:
Вектор столбец 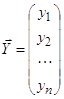 ,
, 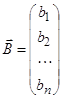 ,
, 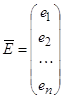 , размерностью n´1.
, размерностью n´1.
Тогда в матричной форме уравнение регрессии записывается так:
![]() .
.
Полуширина доверительного интервала рассчитывается по формуле:
![]() ,
,
где ![]() - среднее квадратическое отклонение остатков;
- среднее квадратическое отклонение остатков;
![]() - критическая точка распределения Стьюдента, соответствующая уровню доверия g=(0.95, 0.99, 0.999) и степени свободы k=n-p-1.
- критическая точка распределения Стьюдента, соответствующая уровню доверия g=(0.95, 0.99, 0.999) и степени свободы k=n-p-1.
вектор 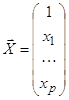 точка из области прогноза.
точка из области прогноза.
2. Задача
Найдите коэффициент эластичности для указанной модели в заданной точке x. Сделать экономический вывод.
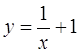
X=1
1. Найдем производную функции 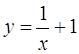 ,
,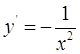
2. Найдем эластичность. ![]() , тогда
, тогда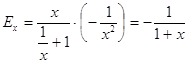
3. Коэффициент эластичности для точки прогноза:
X=1
![]()
Коэффициент эластичности показывает, что при изменении фактора X =1 на 1% показатель Y уменьшится на 0,5%.
3. Задача
Для представленных данных выполнить следующее задание:
1. Провести эконометрический анализ линейной зависимости показателя от первого фактора. Сделать прогноз для любой точки из области прогноза, построить доверительную область. Найти коэффициент эластичности в точке прогноза.
2. Провести эконометрический анализ нелинейной зависимости показателя от второго фактора, воспользовавшись подсказкой. Сделать прогноз для любой точки из области прогноза, построить доверительную область. Найти коэффициент эластичности в точке прогноза.
3. Провести эконометрический анализ линейной зависимости показателя от двух факторов. Сделать точечный прогноз для любой точки из области прогноза. Найти частичные коэффициенты эластичности в точке прогноза.
Производительность труда, фондоотдача и уровень рентабельности по плодоовощным консервным заводам области за год характеризуются следующими данными:
| № района | Фактор | Уровень убыточности продукции животноводства % | ||
| Удельный вес пашни в сельскохозяйственных угодьях % | Удельный вес лугов и пастбищ % | |||
| 1 | 80 | 20 | 20 |
|
| 2 | 87,2 | 12,8 | 37,5 |
|
| 3 | 90,8 | 9,2 | 43,4 |
|
| 4 | 94,7 | 11,3 | 45,6 |
|
| 5 | 81,4 | 18,6 | 23,4 |
|
| 6 | 79,2 | 10,8 | 25 |
|
| 7 | 71,3 | 28,7 | 17,2 |
|
| 8 | 86,2 | 13,8 | 33,3 |
|
| 9 | 71,4 | 28,6 | 15 |
|
| 10 | 77,7 | 22,9 | 18,7 |
|
| 11 | 75,4 | 14 | 24,8 |
|
| 12 | 77,9 | 13 | 34,5 |
|
| 13 | 87,2 | 12,8 | 33,1 |
|
| 14 | 68,1 | 25 | 19,2 |
|
| 15 | 86,2 | 13,8 | 31,8 |
|
Нелинейную зависимость принять 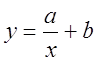
Обозначим вес пашни в с/х % – Х, уровень убыточности (%) – У. Построим линейную зависимость показателя от фактора. Найдем основные числовые характеристики. Объем выборки n=15 – суммарное количество наблюдений. Минимальное значение Х=68,1, максимальное значение Х=94,7, значит, удельный вес пашни меняется от 68,1 до 94,7 %. Минимальное значение У=15, максимальное значение У=46,5, уровень убыточности животноводства от 15 до 46,5%. Среднее значение 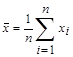 . Среднее значение пашни составляет 80,1%, среднее значение уровня убыточности составляет 28,2%. Дисперсия
. Среднее значение пашни составляет 80,1%, среднее значение уровня убыточности составляет 28,2%. Дисперсия ![]() = 58,83,
= 58,83, ![]() = 92,965. Среднеквадратическое отклонение
= 92,965. Среднеквадратическое отклонение ![]() 7,67, значит среднее отклонение пашни от среднего значения, составляет 7,67%.,
7,67, значит среднее отклонение пашни от среднего значения, составляет 7,67%., ![]() 9,64, значит среднее отклонение уровня убыточности от среднего значения, составляет 9,64%. Определим, связаны ли Х и У между собой, и, если да, то определить формулу связи. По таблице строим корреляционное поле (диаграмму рассеивания) – нанесем точки
9,64, значит среднее отклонение уровня убыточности от среднего значения, составляет 9,64%. Определим, связаны ли Х и У между собой, и, если да, то определить формулу связи. По таблице строим корреляционное поле (диаграмму рассеивания) – нанесем точки ![]() на график. Точка с координатами
на график. Точка с координатами ![]() =(80; 27,08) называется центром рассеяния. По виду корреляционного поля можно предположить, что зависимость между y и x линейная. Для определения тесноты линейной связи найдем коэффициент корреляции:
=(80; 27,08) называется центром рассеяния. По виду корреляционного поля можно предположить, что зависимость между y и x линейная. Для определения тесноты линейной связи найдем коэффициент корреляции: 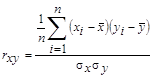 =0,88 Так как
=0,88 Так как ![]() то линейная связь между Х и У достаточная. Пытаемся описать связь между х и у зависимостью
то линейная связь между Х и У достаточная. Пытаемся описать связь между х и у зависимостью![]() . Параметры b0, b1 находим по МНК.
. Параметры b0, b1 находим по МНК. ![]() Так как b1>0, то зависимость между х и y прямая: с ростом пашни уровень убыточности животноводства возрастает. Проверим значимость коэффициентов bi. Значимость коэффициента b может быть проверена с помощью критерия Стьюдента:
Так как b1>0, то зависимость между х и y прямая: с ростом пашни уровень убыточности животноводства возрастает. Проверим значимость коэффициентов bi. Значимость коэффициента b может быть проверена с помощью критерия Стьюдента:
![]() -4,608. Значимость
-4,608. Значимость ![]() равна 0,000490101, т.е практически 0%. Коэффициент b0 статистически не значим.
равна 0,000490101, т.е практически 0%. Коэффициент b0 статистически не значим.
![]() 6,744. Значимость
6,744. Значимость ![]() равна 1,375·10-5, т.е 0%, что меньше, чем 5%. Коэффициент b1 статистически значим. Получили модель зависимости уровня пашни от убыточности животноводства
равна 1,375·10-5, т.е 0%, что меньше, чем 5%. Коэффициент b1 статистически значим. Получили модель зависимости уровня пашни от убыточности животноводства ![]()
После того, как была построена модель, необходимо проверить ее на адекватность.
Для анализа общего качества оцененной линейной регрессии найдем коэффициент детерминации: ![]() =0,777. Разброс данных объясняется линейной моделью на 77,7% и на 22,3% – случайными ошибками. Качество модели плохое.
=0,777. Разброс данных объясняется линейной моделью на 77,7% и на 22,3% – случайными ошибками. Качество модели плохое.
Проверим с помощью критерия Фишера.
Для проверки найдем величины: ![]() 1012,166 и
1012,166 и ![]() 1012,166. Вычисляем k1=1, k2=13. Находим наблюдаемое значение критерия Фишера
1012,166. Вычисляем k1=1, k2=13. Находим наблюдаемое значение критерия Фишера ![]() 45.48. Значимось этого значения a=1,37610-5, т.е. процент ошибки равен 0%, что меньше, чем 5%. Модель
45.48. Значимось этого значения a=1,37610-5, т.е. процент ошибки равен 0%, что меньше, чем 5%. Модель ![]() считается адекватной с гарантией более 95%.
считается адекватной с гарантией более 95%.
Найдем прогноз на основании линейной регрессии. Выберем произвольную точку из области прогноза ![]() , х=80
, х=80
Рассчитываем прогнозные значения по модели для всех точек выборки и для точки прогноза: ![]()
Найдем полуширину доверительного интервала в каждой точке выборки xпр: 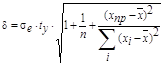
sе – средне квадратичное отклонение выборочных точек от линии регрессии
![]() 4,72
4,72
ty = критическая точка распределения Стьюдента для надежности g=0,9 и k2=13.
n =15.
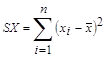
или ![]()
xпр – точка из области прогнозов.
Прогнозируемый доверительный интервал для любого х такой ![]() , где d(х=80)=10,53, т.е. доверительный интервал для хпр=80 составит от 16,55 до 37,61 с гарантией 90%.
, где d(х=80)=10,53, т.е. доверительный интервал для хпр=80 составит от 16,55 до 37,61 с гарантией 90%.
Совокупность доверительных интервалов для всех х из области прогнозов образует доверительную область.
Т.е. при пашни 80 % уровень убытка животноводства составит от 16% до 37,5%.
Найдем эластичность.
Для линейной модели ![]()
![]()
Коэффициент эластичности показывает, что при изменении х=80 на 1% показатель y увеличивается на 3,29%.
Обозначим пашни в с/х – Х, уровень убыточности – У. Построим нелинейную зависимость показателя от фактора вида 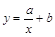 . Найдем основные числовые характеристики. Объем выборки n=15 – суммарное количество наблюдений.
. Найдем основные числовые характеристики. Объем выборки n=15 – суммарное количество наблюдений.
Минимальное значение Х=9.2, максимальное значение Х=28.7, значит, площадь пашен изменяется от 9.2 до 28.7%. Минимальное значение У=15, максимальное значение У=45.6, уровень убыточности животноводства изменяется от 15 до 45.6%. Среднее значение 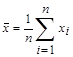 . Среднее значение пашни составляет 17.02%, среднее значение уровня убыточности животноводства составляет 28.17%.
. Среднее значение пашни составляет 17.02%, среднее значение уровня убыточности животноводства составляет 28.17%.
Дисперсия ![]() =42.45,
=42.45, ![]() =92.965.
=92.965.
Среднеквадратическое отклонение ![]() 6.52, значит среднее отклонение объема пашни от среднего значения, составляет 6.52%,
6.52, значит среднее отклонение объема пашни от среднего значения, составляет 6.52%, ![]() 9.64, значит среднее отклонение уровня убыточности животноводства от среднего значения, составляет 9.64%.
9.64, значит среднее отклонение уровня убыточности животноводства от среднего значения, составляет 9.64%.
Определим, связаны ли Х и У между собой, и, если да, то определить формулу связи. По таблице строим корреляционное поле (диаграмму рассеивания) – нанесем точки ![]() на график.
на график.
Точка с координатами ![]() =(17.02; 28.17) называется центром рассеяния.
=(17.02; 28.17) называется центром рассеяния.
По виду корреляционного поля можно предположить, что зависимость между y и x нелинейная.
Пытаемся описать связь между х и у зависимостью![]() . Перейдем к линейной модели. Делаем линеаризующую подстановку:
. Перейдем к линейной модели. Делаем линеаризующую подстановку: ![]() ,
, ![]() . Получили новые данные U и V. Для этих данных строим линейную модель:
. Получили новые данные U и V. Для этих данных строим линейную модель: ![]()
Проверим тесноту линейной связи u и v. Найдем коэффициент корреляции: ![]() 0,864. Между u и v сильная линейная связь.
0,864. Между u и v сильная линейная связь.
Параметры b0, b1 находим по МНК. ![]()
Проверим значимость коэффициентов bi. Значимость коэффициента b может быть проверена с помощью критерия Стьюдента:
![]() =0.845. Значимость
=0.845. Значимость ![]() равна 0,413, т.е практически 41%. Коэффициент b0 статистически не значим.
равна 0,413, т.е практически 41%. Коэффициент b0 статистически не значим.
![]() 6.19 Значимость
6.19 Значимость ![]() равна 0,000032, т.е практически 0%. Коэффициент b1 статистически значим.
равна 0,000032, т.е практически 0%. Коэффициент b1 статистически значим.
Получили линейную модель ![]()
После того, как была построена модель, необходимо проверить ее на адекватность.
Для анализа общего качества оцененной линейной регрессии найдем коэффициент детерминации: ![]() =0,747. Разброс данных объясняется линейной моделью на 75% и на 25% – случайными ошибками. Качество модели хорошее.
=0,747. Разброс данных объясняется линейной моделью на 75% и на 25% – случайными ошибками. Качество модели хорошее.
Проверим с помощью критерия Фишера.
Для проверки находим величины: ![]() 972.42 и
972.42 и ![]() 25.32. Вычисляем k1=1, k2=13. Находим наблюдаемое значение критерия Фишера
25.32. Вычисляем k1=1, k2=13. Находим наблюдаемое значение критерия Фишера ![]() 38.41. Значимось этого значения a=0,000032, т.е. процент ошибки практически равен 0%. Модель
38.41. Значимось этого значения a=0,000032, т.е. процент ошибки практически равен 0%. Модель ![]() считается адекватной с гарантией более 99%.
считается адекватной с гарантией более 99%.
Так как линейная модель адекватна, то и соответствующая нелинейная модель тоже адекватна.
Находим параметры исходной нелинейной модели: а=b1=370.76; = b0=3.53.
Вид нелинейной функции: ![]() .
.
Т.е. зависимость уровня убыточности от площади пашен имеет вид: ![]() .
.
Найдем прогноз на основании модели. Выберем произвольную точку из области прогноза (9.2; 28.7), х=15
Рассчитываем прогнозные значения по модели для всех точек выборки и для точки прогноза: ![]() 28.25
28.25
Найдем полуширину доверительного интервала в каждой точке выборки. Для этого найдем полуширину для линейной модели:
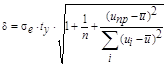
sе – средне квадратичное отклонение выборочных точек от линии регрессии ![]() 5.03
5.03
![]()
uпр – точка из области прогнозов. Прогнозируемый доверительный интервал для любого u такой ![]()
Для нелинейной модели найдем доверительный интервал, воспользовавшись обратной заменой: ![]() Совокупность доверительных интервалов для всех х из области прогнозов образует доверительную область.
Совокупность доверительных интервалов для всех х из области прогнозов образует доверительную область.
Прогноз для х=15 составит от 17.03 до 39.48 с гарантией 90%.
Т.е. при площади пашен 15 уровень убыточности животноводства составит от 17.03% до 39.48%.
Найдем эластичность.
Коэффициент эластичности для точки прогноза:
![]() ,
,
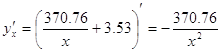
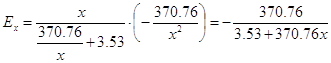
Коэффициент эластичности для точки прогноза:
![]()
Коэффициент эластичности показывает, что при изменении площади паши 15 % на 1% уровень убыточности животноводства увеличивается на 13.12%.
Обозначим удельный вес пашни – Х1 %, удельный вес лугов и пастбищ - Х2 %, уровень убыточности продукции животноводства - У %. Построим линейную зависимость показателя от факторов. Найдем основные числовые характеристики. Объем выборки n=15 – суммарное количество наблюдений. Минимальное значение Х1=68.1, максимальное значение Х1=94.7, значит, удельный вес пашни изменяется от 68.1 до 94.7%. Минимальное значение Х2=9.2, максимальное значение Х2=28.7, значит, вес лугов и пастбищ изменяется от 9.2 до 28.7%. Минимальное значение У=15, максимальное значение У=45.6, уровень убыточности животноводства изменяется от 15 до 45.6%. Среднее значение 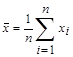 .
.
Среднее значение веса пашни составляет 80.98 %, среднее значение веса лугов и пастбищ составляет 17.02, среднее значение уровня убыточности животноводства составляет 28.17%.
Дисперсия ![]() =58,83,
=58,83, ![]() =42,45
=42,45 ![]() =92.96%.
=92.96%.
Среднеквадратическое отклонение ![]() 7.67, значит среднее отклонение веса пашни от среднего значения, составляет 7.67%., среднеквадратическое отклонение
7.67, значит среднее отклонение веса пашни от среднего значения, составляет 7.67%., среднеквадратическое отклонение ![]() 6.52, значит среднее отклонение удельного веса лугов и пастбищ от среднего значения, составляет 6.52%,
6.52, значит среднее отклонение удельного веса лугов и пастбищ от среднего значения, составляет 6.52%,![]() 9.65, значит среднее отклонение уровня убыточного животноводства от среднего значения, составляет 9.65%.
9.65, значит среднее отклонение уровня убыточного животноводства от среднего значения, составляет 9.65%.
Прежде чем строить модель, проверим факторы на коллинеарность. По исходным данным строим корреляционную матрицу. Коэффициент корреляции между X1 и X2 равен 0,89. Так как ![]() , значит X1 и X2 – неколлинеарные
, значит X1 и X2 – неколлинеарные
Определим, связаны ли Х1, Х2 и У между собой.
Для определения тесноты линейной связи найдем коэффициент корреляции: r=0,892. Так как ![]() то линейная связь между Х1, Х2 и У достаточная.
то линейная связь между Х1, Х2 и У достаточная.
Пытаемся описать связь между х и у зависимостью![]() .
.
Параметры b0, b1,b2 находим по МНК. ![]() .
.
Проверим значимость коэффициентов bi.
Значимость коэффициента b может быть проверена с помощью критерия Стьюдента:
![]() -0,867. Значимость
-0,867. Значимость ![]() равна 0.402, т.е приблизительно 40%. Так как это значение намного больше 5%, то коэффициент b0 статистически не значим.
равна 0.402, т.е приблизительно 40%. Так как это значение намного больше 5%, то коэффициент b0 статистически не значим.
![]() 3.04. Значимость
3.04. Значимость ![]() равна 0.0102, т.е 1%. Так как это значение меньше 5%, то коэффициент b1 статистически значим.
равна 0.0102, т.е 1%. Так как это значение меньше 5%, то коэффициент b1 статистически значим.
![]() -2.107. Значимость
-2.107. Значимость ![]() равна 0.056, т.е 5%. Так как это значение больше 5%, то коэффициент b2 статистически не значим.
равна 0.056, т.е 5%. Так как это значение больше 5%, то коэффициент b2 статистически не значим.
Проверим адекватность.
Для анализа общего качества оцененной линейной регрессии найдем коэффициент детерминации: ![]() =0,8377. Разброс данных объясняется линейной моделью на 84% и на 16% – случайными ошибками. Качество модели хорошее.
=0,8377. Разброс данных объясняется линейной моделью на 84% и на 16% – случайными ошибками. Качество модели хорошее.
Проверим с помощью критерия Фишера.
Для проверки найдем величины: ![]() 545.17 и
545.17 и ![]() 17.6. Вычисляем k1=2, k2=12. Находим наблюдаемое значение критерия Фишера
17.6. Вычисляем k1=2, k2=12. Находим наблюдаемое значение критерия Фишера ![]() 30.98 Значимость этого значения a=0.000018, т.е. процент ошибки равен 0,00018%. Так как это значение меньше 5%, то модель
30.98 Значимость этого значения a=0.000018, т.е. процент ошибки равен 0,00018%. Так как это значение меньше 5%, то модель ![]() считается адекватной с гарантией более 99%.
считается адекватной с гарантией более 99%.
Получили модель зависимости уровня удельного веса пашни от удельного веса лугов и пастбищ и убыточности скотоводства ![]()
Найдем прогноз на основании линейной регрессии. Выберем произвольную точку из области прогноза:![]() х1=80, х2=30. Рассчитываем прогнозные значения по модели для всех точек выборки и для точки прогноза:
х1=80, х2=30. Рассчитываем прогнозные значения по модели для всех точек выборки и для точки прогноза: ![]()
Т.е. при удельном весе пашен 80% и весе лугов и пастбищ 30% уровень убыточности животноводства составит 19.86%.
Найдем эластичность по каждому фактору.
Для линейной модели
![]() ,
,
![]() .
.
Коэффициент эластичности показывает, что увеличении пашен с 80 % на 1% и при уровне лугов 30 %, уровень убыточности увеличится с 19.86 грн на 2.89%.
Для линейной модели
![]() ,
,
![]() .
.
Коэффициент эластичности показывает, что увеличении пашен с 80 % на 1% и при уровне лугов 30 %, уровень убыточности уменьшиться с 19.86 грн на 0.89%.
Для уменьшения убыточности животноводства целесообразней увеличивать вес лугов и пастбищ при неизменном весе пашен.
Использованная литература
1. Экономико-математические методы и прикладные модели: Учебное пособие для вузов / В.В. Федосеев, А.Н. Гармаш и др. - М.: ЮНИТИ, 1999. - 391 с.
2. Орлова И.В. Экономико-математические методы и модели. Выполнение расчетов в среде EXCEL. Практикум: Учебное пособие для вузов. - М.: Финстатинформ, 2000.- 136 с.
3. Компьютерные технологии экономико-математического моделирования: Учебное пособие для вузов / Д.М. Дайитбегов, И.В. Орлова. - М.: ЮНИТИ, 2001.
4. Эконометрика: Учебник / Под ред. И.И. Елисеевой. - М.: Финансы и статистика, 2001.
5. Практикум по эконометрике: Учебное пособие / Под ред. И.И. Елисеевой - М.: Финансы и статистика, 2001.