Обработка статистической информации при определении показателей надежности
Для техники, используемой в сельскохозяйственном производстве, характерно значительное рассеивание показателей надежности из-за нестабильности качества новых или отремонтированных машин и различных условий их эксплуатации. Вследствие этого все показатели надежности автомобилей, тракторов и сельскохозяйственных машин относятся к категории случайных величин, обработка и расчет которых производится методами теории вероятностей и математической статистики.
Существует несколько методов обработки информации. Некоторые из них (например, метод максимального правдоподобия) сложны, трудоемки, нуждаются в применении электронно-вычислительной техники. Использование таких методов в хозяйствах и на ремонтных предприятиях для обработки информации о надежности сельскохозяйственной техники не только затруднено, но и нецелесообразно, т.к. их точность превышает точность исходной информации.
Рассмотренный ниже метод обработки информации прост и надежен. Его могут применять инженеры сельскохозяйственного производства без использования электронно-вычислительных машин.
1 Первичная обработка статистической информации
Основные этапы обработки статистической информации следующие:
- составление сводной таблицы исходной информации в порядке возрастания показателей надежности (вариационный ряд);
- составление статистического ряда;
- определение среднего значения (![]() ) и среднего квадратического отклонения (σ) показателя надежности;
) и среднего квадратического отклонения (σ) показателя надежности;
- проверка информации на выпадающие точки;
- графическое изображение опытной информации (построение полигона и кривой накопленных опытных вероятностей показателя надежности);
- определение коэффициента вариации (υ), характеризующего относительное рассеивание показателя надежности;
- выбор теоретического закона распределения, определение его параметров и графическое построение дифференциальной и интегральной кривых;
- оценка совпадения опытного и теоретического распределений по критериям согласия;
- определение доверительных границ одиночных и средних значений показателя надежности и наибольших возможных ошибок расчета.
Последовательность выполнения расчетов приведена в таблице 1.1.
Таблица 1.1 – Размеры толщины шлиц первичного вала коробки перемены передач ( 50-1701032) трактора МТЗ-50
| № п/п | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Размер, мм | 6,01 | 6,09 | 6,16 | 6,22 | 6,24 | 6,27 | 6,28 | 6,32 | 6,36 | 6,39 | 6,41 | 6,45 | 6,46 | 6,47 |
| № п/п | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| Размер, мм | 6,54 | 6,56 | 6,58 | 6,60 | 6,61 | 6,63 | 6,64 | 6,67 | 6,69 | 6,71 | 6,73 | 6,75 | 6,79 | 6,81 |
| № п/п | 29 | 30 | ||||||||||||
| Размер, мм | 6,84 | 6,96 |
Допустимый размер - 6,45 мм
1.1 Статистический ряд информации
Статистический ряд информации составляется для упрощения дальнейших расчетов в том случае, если повторность исходной информации N не менее 25.
Для построения статистического ряда вся информация разбивается на n интервалов. Ориентировочно количество интервалов определяется по формуле:
![]() , (1.1)
, (1.1)
где n – число интервалов; N – число исследуемых объектов.
Наиболее рациональное количество интервалов, применяемое на практике n=6…14.
Все интервалы должны быть одинаковыми по величине, прилегать друг к другу и не иметь разрывов.
Для нашего случая:
![]() .
.
Ширина интервала «А» ориентировочно определяется по формуле:
![]() , (1.2)
, (1.2)
где tmax – максимальное значение случайной величины;
tmin – минимальное значение случайной величины и округляется до удобной величины.
![]() мм.
мм.
Начало первого интервала принимаем t1Н=6,0 мм.
Статистический ряд представляет из себя таблицу из четырех строк (таблица 1.2). В первой строке указываются границы интервалов, во второй – количество случаев попадания случайной величины в каждом интервале (частота) mi , в третьей – опытная вероятность pi случайной величины, в четвертой – накопленная опытная вероятность![]()
Опытная вероятность определяется как отношение числа случаев mi к общему объему информации N. Так, например, опытная вероятность в первом и втором интервалах равна:
![]() ;
; ![]() .
.
Правильность построения статистического ряда может быть проверена по накопленной вероятности.
Для последнего интервала ![]()
Таблица 1.2 – Статистический ряд информации
| Интервал | 6,00-6,16 | 6,16-6,32 | 6,32-6,48 | 6,48-6,64 | 6,64-6,80 | 6,80-6,96 |
| Частота mi | 3 | 5 | 6 | 7 | 6 | 3 |
| Опытная вероятность Pi | 0,1 | 0,17 | 0,2 | 0,23 | 0,2 | 0,1 |
| Накопленная опытная вероятность ∑Pi | 0,1 | 0,27 | 0,47 | 0,7 | 0,9 | 1 |
| Середина | 6,08 | 6,24 | 6,40 | 6,56 | 6,72 | 6,88 |
1.2 Определение среднего значения и среднеквадратического отклонения показателей надежности
Среднее значение является важнейшей характеристикой показателя надежности. На основании средних значений производится планирование работы машины, определение объемов ремонтных работ, составление заявок на запасные части и т.д.
Точность определения среднего значения возрастает по мере увеличения повторности информации, приближаясь к своему пределу – математическому ожиданию.
При наличии статистического ряда среднее значение показателя надежности ![]() определяется по уравнению:
определяется по уравнению:
![]() (1.3)
(1.3)
где n – количество интервалов в статистическом ряду;
ti – значение середины i-го интервала;
pi – опытная вероятность i-го интервала.
Средний размер толщины шлиц первичного вала коробки передач, определенный по уравнению 1.3 с использованием статистического ряда будет равен:
![]() .
.
Среднеквадратичное отклонение s является абсолютной характеристикой рассеивания показателя надежности, позволяющей переходить от общей совокупности к показателям надежности отдельных машин. При наличии статистического ряда информации среднее квадратическое отклонение определяется по уравнению:
![]() (1.4)
(1.4)
Среднеквадратическое отклонение размера толщины шлиц первичного вала коробки передач, определенного по уравнению 1.4, равно:
![]() =0,24 мм.
=0,24 мм.
1.3 Проверка информации на выпадающие точки
Опытная информация по показателям надежности, полученная в процессе наблюдения за машинами в условиях рядовой эксплуатации, может иметь ошибочные точки, выпадающие из общего закона распределения. Причиной появления выпадающих точек могут быть грубые ошибки в измерениях, ошибочные записи и т.д.
Поэтому, перед окончательной математической обработкой, информация должна быть проверена на выпадающие точки. Проверке обычно подвергаются первые и последние точки.
Первый способ проверки информации на выпадающие точки заключается в
проверке по правилу ![]() . Так как, при законе нормального распределения 99,7% всех точек находятся в интервале
. Так как, при законе нормального распределения 99,7% всех точек находятся в интервале ![]() , то все точки, входящие в этот интервал, считаются действительными.
, то все точки, входящие в этот интервал, считаются действительными.
Для рассматриваемого примера границы достоверности точек информации будут соответственно равны:
нижняя граница: ![]()
верхняя граница: ![]()
Наименьший размер толщины шлиц первичного вала ![]() , что больше
, что больше ![]() , следовательно, первая точка информации достоверна и должна учитываться при дальнейших расчетах.
, следовательно, первая точка информации достоверна и должна учитываться при дальнейших расчетах.
Наибольший размер толщины шлиц первичного вала ![]() , что меньше
, что меньше ![]() , следовательно, последняя точка информации достоверна и должна учитываться при дальнейших расчетах.
, следовательно, последняя точка информации достоверна и должна учитываться при дальнейших расчетах.
Второй способ проверки достоверности точек производится по критерию l (критерий Ирвина). Этот способ является более точным. При этом определяется опытное значение критерия lоп по формуле:
![]() , (1.5)
, (1.5)
где ti+1, ti – смежные точки информации , и сравниваются с нормированным значением l.
Если λоп < λ точка достоверна;
λоп > λ точка недостоверна.
Проведя проверку крайних точек информации по доремонтным ресурсам толщины зуба третьей передачи, получим
для наименьшей точки информации (![]() )
)
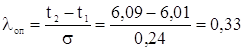 ;
;
для наибольшей точки информации (![]() )
)
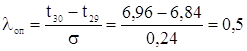 .
.
Для объема информации N=30 и доверительной вероятности α=0,95 нормированное значение критерия λ=1,2.
Сравнение опытных значений критерия Ирвина с нормированным его значением показывает, что первая точка информации ![]() является достоверной, λоп =0,16 < λ=1,2 и её следует учитывать в дальнейших расчетах. Последняя точка информации
является достоверной, λоп =0,16 < λ=1,2 и её следует учитывать в дальнейших расчетах. Последняя точка информации ![]() также является достоверной, λоп =0,32 < λ=1,2 и её тоже следует учитывать в дальнейших расчетах.
также является достоверной, λоп =0,32 < λ=1,2 и её тоже следует учитывать в дальнейших расчетах.
В случаях, когда исключаются выпадающие точки, нужно перестроить статистический ряд и пересчитать среднее значение и среднее квадратическое отклонение показателя надежности.
1.4 Графическое изображения опытного распределения
По данным статистического ряда могут быть построены полигон и кривая накопленных опытных вероятностей (рисунки 1.1 и 1.2 в приложении), которые дают наглядное представление об опытном распределении показателя надежности.
При выборе масштаба при построении графиков желательно придерживаться правила «золотого сечения», т.е.
![]() , (1.6)
, (1.6)
где y – максимальное значение ординаты;
x – максимальное значение абсциссы.
При построении полигона распределения по оси абсцисс откладывают в определенном масштабе показатель надежности t, а по оси ординат - опытную частоту mi или опытную вероятность Pi.
Для построения кривой накопленных опытных вероятностей по оси абсцисс откладывают в масштабе значения показателя надежности t, а по оси ординат – накопленную опытную вероятность ∑ Pi.
Точки полигона образуются пересечением ординаты, равной опытной вероятности интервала, и абсциссы, равной середине этого интервала. Точки кривой накопленных опытных вероятностей образуются пересечением ординаты, равной сумме опытных вероятностей и абсциссы - конца данного интервала.
Полигон дает наглядное представление о распределении показателя надежности. Кривая накопленных опытных вероятностей в этом отношении менее наглядна, но с её помощью удобно решать некоторые инженерные задачи.
1.5 Определение коэффициента вариации
Коэффициент вариации – это относительная характеристика случайной величины, используется при выборе теоретического закона распределения. Коэффициент вариации υ равен отношению σ к среднему значению показателя надежности ![]()
![]() (1.7)
(1.7)
Определение коэффициента вариации по уравнению 1.7 выполняется для тех показателей надежности, зона рассеивания которых начинается от их нулевого значения или близка к нему.
При наличии смещения начала зоны рассеивания tсм величина коэффициента вариации определяется по уравнению:
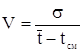 (1.8)
(1.8)
Учет смешения особенно необходим тогда, когда для выравнивания опытной информации используется теоретический закон распределения Вейбулла, параметры которого непосредственно зависят от величины коэффициента вариации.
Величину смещения tсм , с достаточной для практических расчетов точностью при наличии статистического ряда можно определить:
![]() (1.9)
(1.9)
При отсутствии статистического ряда за смещение принимается величина:
![]() (1.10)
(1.10)
где t1, t2, t3 – значения первого, второго и третьего показателей надежности в порядке возрастания.
Для нашего случая величина смещения равна:
![]()
Тогда коэффициент вариации, определенный по формуле 1.8 будет равен:
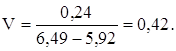
1.6 Выбор теоретического закона распределения
Теоретический закон распределения (ТЗР) выражает общий характер изменения показателя надежности и исключает частные отклонения, связанные с недостатком первичной информации, т.е. ТЗР характеризует генеральную совокупность. Опытное распределение имеет частные особенности, которые должны быть исключены при переносе характеристик опытного распределения на генеральную совокупность.
Процесс замены опытных закономерностей теоретическими называется выравнивание опытной информации.
Каждый ТЗР характеризуется двумя функциями:
f(t) – дифференциальная функция;
F(t) – интегральная функция.
Применительно к показателям надежности машин, эксплуатируемых в сельском хозяйстве, в подавляющем большинстве случаев используется закон нормального распределения (ЗНР) и закон распределения Вейбулла (ЗРВ).
Выбор теоретического закона производится исходя из следующих признаков:
По величине коэффициента вариации:
если V < 0,3 – выбирается ЗНР;
если 0,3 < V < 0,5 – выбирается ЗНР или ЗРВ;
если V > 0,5 – выбирается ЗРВ.
По области применения.
ЗНР применяется, как правило при определении характеристик рассеивания:
ресурсов и сроков службы машин и агрегатов;
времени и стоимости восстановления работоспособности машин;
наработка на ресурсный отказ;
ошибок измерений размеров деталей.
б) ЗРВ применяется, как правило, при определении:
ресурсов и сроков службы отдельных деталей и сопряжений;
доремонтных и межремонтных ресурсов тех элементов машин, отказы которых вызваны выходом из строя одной и той же детали;
информации по износам деталей.
Здесь применим закон нормального распределения и закон распределения Вейбулла.
Закон нормального распределения (ЗНР)
Отличительной особенностью ЗНР является симметричное рассеивание частных значений относительного среднего.
Дифференциальная функция нормального распределения имеет вид
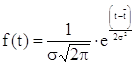 (1.11)
(1.11)
где е = 2,718 – основание натурального логарифма;
![]() - среднее значение показателя надежности;
- среднее значение показателя надежности;
σ – среднее квадратическое отклонение;
π – 3,14;
t – текущее значение показателя надежности.
Интегральное функция или функция распределения F(t) определяется интегрированием функции плотности вероятностей f (t) и имеет вид
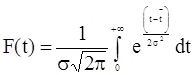 . (1.12)
. (1.12)
Обе эти функции имеют два параметра: ![]() - параметр масштаба и σ – параметр формы. Эти параметры определяются на основании опытной информации. Найденные параметры можно подставить в уравнения 1.11 и 1.12 и использовать ими, но это довольно сложная задача.
- параметр масштаба и σ – параметр формы. Эти параметры определяются на основании опытной информации. Найденные параметры можно подставить в уравнения 1.11 и 1.12 и использовать ими, но это довольно сложная задача.
Если в уравнении 1.11 значение ![]() приравнять к нулю, σ к единице, то получим центрированную и нормированную дифференциальную функцию
приравнять к нулю, σ к единице, то получим центрированную и нормированную дифференциальную функцию
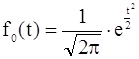 . (1.13)
. (1.13)
Из уравнений 1.11 и 1.13 соотношение между ![]() (t) и
(t) и ![]() (t) имеет вид:
(t) имеет вид:
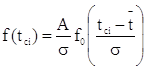 . (1.14)
. (1.14)
Из уравнения 1.13 также следует, что
![]() ,
,
где ![]() - значение середины i-го интервала статистического ряда.
- значение середины i-го интервала статистического ряда.
Центрированная и нормированная интегральная функция (t = 0; σ = 1) определяется по уравнеию:
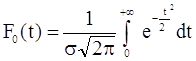 . (1.15)
. (1.15)
Из уравнений 1.12 и 1.15 получим:
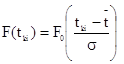 . (1.16)
. (1.16)
где ![]() - значение конца i-го интервала статистического ряда.
- значение конца i-го интервала статистического ряда.
Из уравнения 1.15 следует,
![]() (1.17)
(1.17)
При обработке опытной информации установлено:
- средний ресурс ![]() =6,49 мм;
=6,49 мм;
- среднее квадратическое отклонение σ = 0,24 мм;
- коэффициент вариации V = 0,42.
Для построения дифференциальной кривой f(t) определяется теоретическая вероятность попадания случайной величины в каждом интервале статистического ряда (таблица 1.2).
Так, вероятность того, что деталь потребует ремонта в первом и втором интервале наработок будет равна:
![]()
![]()
и т.д. для остальных интервалов.
Результаты расчетов представлены в таблице 1.3.
Для построения интегральной кривой определяются значения функции F(t) для концов интервалов статистического ряда.
Для первого интервала получим:
![]() ;
;
![]() .
.
Дальнейшие результаты расчетов представлены в таблице 1.3.
Таблица 1.3 – Значения f(t) и F(t) при ЗНР
| Интервалы, мм | 6,00-6,16 | 6,16-6,32 | 6,32-6,48 | 6,48-6,64 | 6,64-6,80 | 6,80-6,96 |
| f(t) | 0,061 | 0,153 | 0,245 | 0,243 | 0,166 | 0,071 |
| F(t) | 0,085 | 0,239 | 0,484 | 0,732 | 0,902 | 0,975 |
Закон распределения Вейбулла (ЗРВ)
Отличительной особенностью закона распределения Вейбулла является правосторонняя асимметрия дифференциальной функции.
Дифференциальная f(t) и интегральная F(t) функции определяются уравнениями:
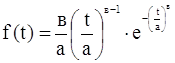 (1.18)
(1.18)
![]() (1.19)
(1.19)
где а и в – параметры распределения Вейбулла.
Определение параметров "а" и "в" аналитическим путем довольно трудоемко, поэтому на практике при их определении пользуются специальными таблицами.
Порядок определения дифференциальной и интегральной функций при ЗРВ следующий:
1. Определение, на основании опытной информации, среднего значения случайной величины ![]() , среднего квадратического отклонения σ и коэффициента вариации.
, среднего квадратического отклонения σ и коэффициента вариации.
2. По таблицам по известному значению коэффициента вариации V определяются параметр "в" и коэффициенты Вейбулла Кв и Св .
3. Параметр "а" определяется из выражения:
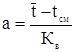 (1.20)
(1.20)
или
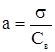 (1.21)
(1.21)
Для рассматриваемого задания по ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Из литературных источников по известному коэффициенту вариации V получим ![]() ; Кв=0,887; Св=0,380.
; Кв=0,887; Св=0,380.

4. Зная параметры "а" и "в" и пользуясь табулированными функциями аf(t) и F(t), можно определить дифференциальную и интегральную функции.
При нахождении функции f(t) для каждого интервала статистического ряда определяется отношение ![]() , где tci – середина i-го интервала. По найденному отношению при определенной величине параметра "в" по таблице определяем значение функции аf(tci-tсм), нормированной по "а".
, где tci – середина i-го интервала. По найденному отношению при определенной величине параметра "в" по таблице определяем значение функции аf(tci-tсм), нормированной по "а".
Значение функции f(t) для i-го интервала статистического ряда определится из выражения:
![]() (1.22)
(1.22)
Для нахождения функции F(t) для каждого интервала определяется отношение ![]() , где tкi – конец i-го интервала. По найденному отношению и параметру "в" по таблице определяем значение интегральной функции F(tкi – tсм).
, где tкi – конец i-го интервала. По найденному отношению и параметру "в" по таблице определяем значение интегральной функции F(tкi – tсм).
Для данного задания значение дифференциальной и интегральной функций при ЗРВ будут равны:
для первого интервала
![]()
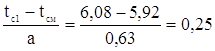 в=2,5
в=2,5 ![]()
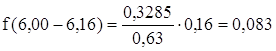
![]()
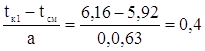 в=2,5 F(tк1)= 0,096
в=2,5 F(tк1)= 0,096
для второго интервала
![]()
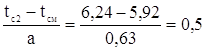 в=2,5
в=2,5 ![]()
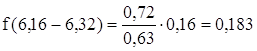
![]()
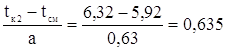 в=2,5 F(tк1)=0,243
в=2,5 F(tк1)=0,243
Дальнейшие результаты расчетов представлены в таблице 1.4.
Графическое изображение дифференциальной функции f(t) и интегральной функции F(t) при выравнивании по ЗНР и по ЗРВ представлено на рисунке 1.1 и 1.2 в приложении.
Таблица 1.4 – Значения f(t) и F(t) при ЗРВ
| Интервалы, мм | 6,00-6,16 | 6,16-6,32 | 6,32-6,48 | 6,48-6,64 | 6,64-6,80 | 6,80-6,96 |
| f(t) | 0,083 | 0,183 | 0,247 | 0,234 | 0,15 | 0,069 |
| F(t) | 0,096 | 0,243 | 0,536 | 0,719 | 0,902 | 0,969 |
1.7 Критерии согласия опытных и теоретических распределений показателей надежности
Применительно к показателям надежности тракторов и сельскохозяйственных машин, чаще используется критерий согласия Пирсона χ2.
Критерий χ2 определяется по формуле:
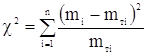 , (1.23)
, (1.23)
где n – число интервалов в статистическом ряду;
mi – опытная частота в i-ом интервале;
mтi – теоретическая частота в i-ом интервале.
![]() (1.24)
(1.24)
Для определения критерия согласия χ2 нужно иметь статистический ряд, который удовлетворяет условиям:
![]()
![]() . (1.25)
. (1.25)
В случае, если статистический ряд не удовлетворяет этим условиям, проводится укрупнение его путем объединения интервалов с частотой mi или mтi меньше 5 с соседними.
Для данного задания значение теоретической частоты (mтi) для каждого интервала статистического ряда, определенное по формуле 1.24 для ЗНР и ЗРВ представлено в таблице 1.5.
Таблица 1.5 – Значение теоретической частоты для ЗНР и ЗРВ
| Интервалы, мм | 6,00-6,16 | 6,16-6,32 | 6,32-6,48 | 6,48-6,64 | 6,64-6,80 | 6,80-6,96 | |
| Опытная частота mi | 3 | 5 | 6 | 7 | 6 | 3 | |
| F (t) | ЗНР | 0,085 | 0,239 | 0,484 | 0,732 | 0,902 | 0,975 |
| ЗРВ | 0,096 | 0,243 | 0,536 | 0,719 | 0,902 | 0,969 | |
| Теоретическая частота, mтi | ЗНР | 2,55 | 4,62 | 7,35 | 7,44 | 5,1 | 2,19 |
| ЗРВ | 2,88 | 4,41 | 8,79 | 5,49 | 5,49 | 2,01 | |
Так как при выравнивании по ЗНР статистический ряд не удовлетворяет условию 1.25, производим укрупнение статистического ряда, т.е. объединяем первый и второй, а также пятый и шестой интервалы. Укрупненный статистический ряд представлен в таблице 1.6.
Таблица 1.6 – Укрупненный статистический ряд для определения критерия согласия χ2
| Интервалы, мм | 6,00-6,32 | 6,32-6,48 | 6,48-6,64 | 6,64-6,96 | |
| Опытная частота, mi | 8 | 6 | 7 | 9 | |
| Теоретическая частота, mтi | ЗНР | 7,17 | 7,35 | 7,44 | 7,29 |
| ЗРВ | 7,29 | 8,79 | 5,49 | 7,5 | |
Критерий χ2 будет соответственно равен:
- для закона нормального закона
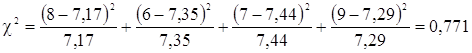 .
.
- для закона распределения Вейбулла
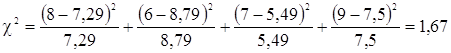 .
.
Для количественной оценки совпадения опытного и теоретического распределения определяется вероятность совпадения по критерию Пирсона Р(χ2), определяемая по таблицам в литературных источниках.
Вероятность совпадения при прочих равных условиях зависит также от повторности исследуемой информации. Для пользования таблицей необходимо определить число степеней свободы "r" по уравнению:
![]() (1.26)
(1.26)
где ny – число интервалов укрупненного статистического ряда;
к – число параметров теоретического закона распределения;
1 – связь, накладываемая закономерностью ∑Pi=1.
Для данного примера ![]()
Тогда для закона нормального распределения Р(χ2) = 40%, для закона распределения Вейбулла Р(χ2) = 20%.
Принято считать, что теоретический закон согласуется с опытным распределением, если Р(χ2)≥10%.
Из проведенной проверки следует, что оба теоретические закона согласуются с опытным распределением, но вероятность совпадения закона нормального распределения несколько выше, чем закон распределения Вейбулла.
1.8 Определение доверительных границ рассеивания одиночного и среднего значений показателя надежности. Абсолютная и относительная предельные ошибки
Доверительные границы рассеивания показателей надежности при использовании закона нормального распределения определяется по формулам:
а) для одиночного значения показателя надежности
![]() ; (1.27)
; (1.27)
![]() ; (1.28)
; (1.28)
![]() ; (1.29)
; (1.29)
![]() , (1.30)
, (1.30)
где ![]() - нижняя доверительная граница одиночного значения показателя надежности;
- нижняя доверительная граница одиночного значения показателя надежности;
![]() - верхняя доверительная граница одиночного значения показателя надежности;
- верхняя доверительная граница одиночного значения показателя надежности;
σ – среднее квадратическое отклонение;
![]() - коэффициент Стьюдента определяется по таблице в зависимости от принятой доверительной вероятности α и объема информации N;
- коэффициент Стьюдента определяется по таблице в зависимости от принятой доверительной вероятности α и объема информации N;
![]() - доверительный интервал;
- доверительный интервал;
![]() - абсолютная ошибка рассеивания.
- абсолютная ошибка рассеивания.
б) для среднего значения показателя надежности:
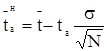 ; (1.31)
; (1.31)
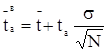 ; (1.32)
; (1.32)
![]() ; (1.33)
; (1.33)
![]() , (1.34)
, (1.34)
где - ![]() - нижняя доверительная граница рассеивания среднего значения показателя надежности;
- нижняя доверительная граница рассеивания среднего значения показателя надежности;
![]() - верхняя доверительная граница рассеивания среднего значения показателя надежности;
- верхняя доверительная граница рассеивания среднего значения показателя надежности;
![]() - абсолютная ошибка рассеивания среднего значения показателя надежности.
- абсолютная ошибка рассеивания среднего значения показателя надежности.
Относительная ошибка переноса опытных значений показателя надежности на генеральную совокупность:
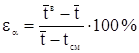 (1.35)
(1.35)
Определяем доверительные границы рассеивания одиночного и среднего значений показателя надежности, предварительно задаемся доверительной вероятностью α = 0,95. По таблице определяем значение коэффициента Стьюдента ![]() для α = 0,95 и N = 30. Для заданных условий
для α = 0,95 и N = 30. Для заданных условий ![]() = 2,04. Тогда, по формулам 1.27, 1.28, 1.30 и 1.31 определим:
= 2,04. Тогда, по формулам 1.27, 1.28, 1.30 и 1.31 определим:
![]() мм;
мм;
![]() мм;
мм;
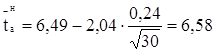 мм;
мм;
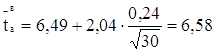 мм;
мм;
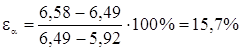
Расчет доверительных границ рассеивания при использовании закона распределения Вейбулла ведется от нуля, т.к. кривая распределения в этом случае асимметрична.
Рассеивание одиночных значений показателя надежности определяется по формулам:
 , (1.36)
, (1.36)
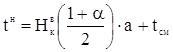 (1.37)
(1.37)
где tн – нижняя доверительная граница;
tв – верхняя доверительная граница;
![]() – нормированная квантиль закона распределения Вейбулла, определяется по таблице из литературных источников для известных значений "в" и
– нормированная квантиль закона распределения Вейбулла, определяется по таблице из литературных источников для известных значений "в" и ![]() ;
;
а – параметр распределения Вейбулла.
Для определения границ рассеивания среднего значения используются формулы:
![]() , (1.38)
, (1.38)
![]() , (1.39)
, (1.39)
где ![]() – нижняя доверительная граница;
– нижняя доверительная граница;
![]() – верхняя доверительная граница;
– верхняя доверительная граница;
r1; r3 – коэффициенты Вейбулла, определяются по таблице из литературы;
в – параметр распределения Вейбулла.
При доверительной вероятности α=0,95; ![]() =6,49 мм; tсм=5,92 мм; в=2,5; а=0,63 мм доверительные границы рассеивания одиночного и среднего значения определенные по формулам 1.21…1.24 будут равны:
=6,49 мм; tсм=5,92 мм; в=2,5; а=0,63 мм доверительные границы рассеивания одиночного и среднего значения определенные по формулам 1.21…1.24 будут равны:
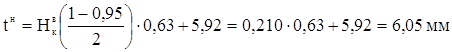
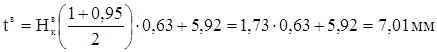
![]()
![]()
Относительная ошибка рассеивания (переноса) опытных значений показателя надежности на генеральную совокупность:
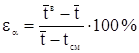 (1.40)
(1.40)
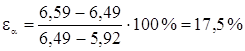
1.9 Определение минимального числа объектов наблюдения при оценке показателей надежности
Точность определения показателей надежности зависит при прочих равных условиях от объема информации, т.е. от числа испытуемых объектов. Как известно, с увеличением количества испытуемых объектов N доверительные границы сближаются, а абсолютная ошибка уменьшается.
Прежде чем приступить к испытанию, нужно определить количество испытуемых изделий. Для этого задаются определенной доверительной вероятностью α и возможной относительной ошибкой εα.
В условиях производства при испытании на надежность в большинстве случаев задаются доверительной вероятностью α=0,80…0,95 и величиной относительной ошибки εα=10…20%. Количество объектов испытания определяется в соответствии с принятым законом распределения.
При использовании закона нормального распределения, если обе части уравнения 1.34 разделить на среднее значение показателя надежности ![]() , получим:
, получим:
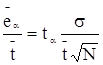 или
или ![]() .
.
Окончательно получим:
![]() . (1.41)
. (1.41)
Для определения объема испытаний N необходимо задаться величиной допустимой относительной ошибкой ![]() и для известной величины коэффициента вариации V определить значение
и для известной величины коэффициента вариации V определить значение ![]() с использование формулы 1.41, затем по таблице определить искомый объем информации N при заданной доверительной вероятности α.
с использование формулы 1.41, затем по таблице определить искомый объем информации N при заданной доверительной вероятности α.
В нашем случае относительная ошибка ![]() ≤20% (0,20), доверительная вероятность α.=0,95, коэффициент вариации V=0,42. Подставляя данные в формулу 1.41 получим
≤20% (0,20), доверительная вероятность α.=0,95, коэффициент вариации V=0,42. Подставляя данные в формулу 1.41 получим
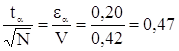 .
.
По таблице для α.=0,95 N=20.
При использовании закона распределения Вейбулла пользуются уравнением:
![]() , (1.42)
, (1.42)
где в – параметр распределения Вейбулла.
По значению q, при известной доверительной вероятности по таблице определяется количество испытуемых объектов.
Для V = 0,42; в=2,5 получим
![]()
По таблицам для α=0,95 находим N=17.
2 Методы обработки усеченной информации
Проводить ресурсные испытания тракторов и автомобилей, обладающих достаточно высокой долговечностью, до получения показателей долговечности у всех объектов практически невозможно. Это требует очень длительного времени их испытаний. Поэтому, при сборе информации по показателям долговечности таких машин, испытания ведут до определенной наработки «Т». При этом длительность испытаний выбирается таким образом, чтобы получить показатели надежности не менее чем у 50% изделий.
Полученная при таких испытаниях информация называется усеченной.
В случае усеченной информации получить характеристики распределения (![]() и σ) изложенным выше методом невозможно. Эту задачу можно решить графическим методом обработки статистической информации с помощью вероятностной бумаги.
и σ) изложенным выше методом невозможно. Эту задачу можно решить графическим методом обработки статистической информации с помощью вероятностной бумаги.
2.1 Вероятностная бумага закона нормального распределения
Порядок пользования вероятностной бумагой закона нормального распределения следующий:
1. На листе бумаги наносят прямоугольные оси координат.
2. На график наносят 6…7 опытных точек, равномерно расположенных в сводной таблице исходной информации (вариационном ряду). При этом координаты точек определяют по уравнениям:
![]() , (2.1)
, (2.1)
где МХ – масштаб по оси Х;
ti – значение показателя надежности i–й точки.
![]() , (2.2)
, (2.2)
где МУ – масштаб по оси "у" (принимается ![]() = 50 мм/ед.квантили);
= 50 мм/ед.квантили);
НК – нормированная квантиль нормального закона распределения определяется по таблице для накопленной опытной вероятности рассматриваемой точки информации ![]() ;
;
«+» - если ![]() «-» - если
«-» - если ![]()
Накопленная опытная вероятность рассматриваемой точки информации определяется по формуле:
![]() , (2.3)
, (2.3)
где ![]()
![]() – порядковый номер i–ой точки вариационного ряда
– порядковый номер i–ой точки вариационного ряда
статистической информации;
N – объем информации.
3. Нанести опытные точки на график и через них провести прямую линию таким образом, чтобы точки были максимально приближены к этой прямой
4. Определяем ![]() и σ. Для этого через координату "у" = 116,5 мм, что соответствует
и σ. Для этого через координату "у" = 116,5 мм, что соответствует ![]() , провести прямую, параллельную оси "х" до пересечения с графиком. Абсцисс точки графика, соответствующая
, провести прямую, параллельную оси "х" до пересечения с графиком. Абсцисс точки графика, соответствующая ![]() , равна
, равна ![]() . Для определения σ через координату "у" = 66,6 мм, что соответствует
. Для определения σ через координату "у" = 66,6 мм, что соответствует ![]() , провести прямую, параллельную оси "х", до пересечения с графиком. Разность абсцисс точек
, провести прямую, параллельную оси "х", до пересечения с графиком. Разность абсцисс точек