Межотраслевой баланс производства и распределения продукции отраслей материального производства
Министерство образования и науки РФ
ГОУ ВПО «Кемеровский государственный университет»
Экономический факультет
Кафедра маркетинга
Контрольная работа
По дисциплине: Экономико-математические методы и модели
На тему: Межотраслевой баланс производства и распределения продукции отраслей материального производства
Научный руководитель: Лысенко Елена Александровна
Работу выполнил: студент 4 курса, группы Э-051
Багдасарян Армен Жирайрович
Кемерово 2008
Экономика условно разделена на четыре сектора (А, Б, В и Г).
Таблица 1. Коэффициенты прямых материальных затрат
| 0.11 | 0.10 | 0.06 | 0.15 |
| 0.05 | 0.00 | 0.04 | 0.12 |
| 0.15 | 0.05 | 0.04 | 0.07 |
| 0.15 | 0.07 | 0.07 | 0.05 |
Таблица 2. Объемы конечной продукции
| Отрасли экономики | |||
| А | Б | В | Г |
| 350 | 300 | 250 | 200 |
Таблица 3. Цены на продукцию отраслей
| Отрасли экономики | |||
| А | Б | В | Г |
| 5 | 15 | 5 | 10 |
Таблица 4. Изменение удельной условно-чистой продукции, %
| Отрасли экономики | |||
| А | Б | В | Г |
| - | 10 | -15 | - |
1.Обозначим черезXi(i=l, n) валовую продукцию i-ой отрасли.
Введем в рассмотрениеxij, (i=l, n), которое выражает количество продукции i-ой отрасли необходимое для производства продукции j-ой отрасли. Хij, (i=1, n) еще называют производственно-эксплуатационными нуждами отраслей, а также межотраслевыми поставками.
Обозначим черезYj, (i=l, ) конечную продукцию i-ой отрасли.
Наконец, обозначим черезZj, (j=l, ) условно чистую продукцию j-ой отрасли.
В данной задаче система уравнений будет иметь вид:
X1 = 0.07x1 + 0.10x2 + 0.00x3 + 0.15x4 + 350
![]() X2 = 0.03x1 + 0.03x2 + 0.04x3 + 0.12x4 + 250
X2 = 0.03x1 + 0.03x2 + 0.04x3 + 0.12x4 + 250
X3 = 0.15x1 + 0.05x2 + 0.04x3 + 0.07x4 + 200
X4 = 0.10x1 + 0.07x2 + 0.10x3 + 0.05x4 + 150
Решение может быть найдено как с помощью точных (прямых) методов, так и с помощью приближенных (итерационных) методов.
Прямые методы позволяют найти точное решение за конечное число шагов.
Итерационные методы теоретически также позволяют найти точное решение, но при этом число шагов будет бесконечным.
Приближенными методами решения данной системы уравнений являются метод простой итерации и метод Зейделя, позволяющие найти приближенный ответ с определенной точностью. Процесс вычислений продолжается до тех пор, пока не будет выполнено условие:
| Xj(k)- Xj(k-1) |![]() е, (i = l,n)
е, (i = l,n)
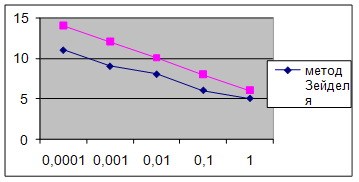
Результаты вычислений приведены в следующих таблицах:
Метод простой итерации
| e | 0,0001 | 0,001 | 0,01 | 0.1 | 1 |
| X1 | 534,704 | 534,704 | 534,704 | 534,704 | 534,704 |
| X2 | 696,226 | 696,226 | 696,226 | 696,226 | 696,226 |
| Хз | 337,313 | 337,313 | 337,313 | 337,313 | 337,313 |
| X4 | 396,857 | 396,857 | 396,857 | 396,857 | 396,857 |
| Количество итераций | 14 | 12 | 10 | 8 | 6 |
Метод Зейделя
Процесс вычисления в методе Зейделя продолжается до тех пор, пока не будут выполнены те же условия, что и в методе простой итерации.
Надо заметить, что метод Зейделя сходится к точному решению быстрее, чем метод простой итерации. Метод Зейделя
| e | 0,0001 | 0,001 | 0,01 | 0.1 | 1 |
| X1 | 534,704 | 534,704 | 534,704 | 534,704 | 534,704 |
| X2 | 696,226 | 696,226 | 696,226 | 696,226 | 696,226 |
| Х3 | 337,313 | 337,313 | 337,313 | 337,313 | 337,313 |
| X4 | 396,857 | 396,857 | 396,857 | 396,857 | 396,857 |
| Количество итераций | 11 | 9 | 8 | 6 | 5 |
На графике показана зависимость количества итераций от точности решения и применяемого метода.
Исследование числа итераций метод простой итерации -метод Зейделя
2. При рассмотрении межотраслевого баланса с использованием натуральных единиц измерения мы приходим к натуральному межотраслевому балансу. Он имеет следующий вид:
Xj=Σxij + Zi, j = l,n;
Xi=Σxij + Yi, i=l,n;
xij=aij*Xj, i,j=1,n
Найдем производственно-эксплуатационные нужды отраслей при заданных прямых материальных затратах и объемах валовой продукции.
a11x1+ a12x2 + a13x3+a14x4
 a21x1+ a22x2 + a23x3+a24x4
a21x1+ a22x2 + a23x3+a24x4
a31x1+ a32x2 + a33x3+a34x4
a41x1+ a42x2 + a43x3+a44x4

0,11*534,704 0,10*696,226 0,06*337,313 0,15*369,857 58,8 69,62 20,24 55,48
![]() 0,05*534,704 0,00*696,226 0,04*337,313 0,12*369,857 26,73 0 13,49 44,38
0,05*534,704 0,00*696,226 0,04*337,313 0,12*369,857 26,73 0 13,49 44,38

0,15*534,704 0,05*696,226 0,04*337,313 0,07*369,857 80,2 34,8 13,49 25,89
0,15*534,704 0,07*696,226 0,07*337,313 0,05*369,857 80,2 48,74 23,61 18,49
Натуральный межотраслевой баланс
| Отрасли | А | Б | В | Г | Σ | Y | X |
| А | 58,8 | 69,62 | 20,24 | 55,48 | 102,7 | 350,01 | 452,708 |
| Б | 13,58 | 9,51 | 12,58 | 31,44 | 67.И | 250,01 | 317,127 |
| В | 67,91 | 15,85 | 12,58 | 18,34 | 114,68 | 200.02 | 314,693 |
| Г | 45,27 | 22,19 | 31,46 | 13,1 | 112,02 | 150,02 | 262,041 |
| Σ | 158,45 | 79,26 | 56,62 | 102,18 | 396,51 | ||
| Z | 294,26 | 237,86 | 258,07 | 159,86 | |||
| X | 452,708 | 317,127 | 314,693 | 262,041 | |||
В сводном материальном балансе все показатели даются в денежном или стоимостном выражении. При этом каждый продукт оценивается по единой цене независимо от того, где он используется. Это главное условие сводного материального баланса.
Для того, чтобы перейти от натурального баланса к стоимостному умножим каждое уравнение межотраслевого баланса на соответствующую цену продукции отрасли.
Получаем:
Хi*Рi = Σаij,*Хj*Рi+Yi*Рi, i = l,n;
Обозначим через:
Xi = Xi * Рi -стоимостное выражение валовой продукции i-oй отрасли;
Yi = Yi * Pi - стоимостное выражение конечной продукции;
Подставим:
Xi = Σaij* Xj * (Pj/Pj) * Pi + Yi, i=l,n;
Xi= Σaij*Xj + Yi ; i=l,n;
Коэффициенты сводного материального баланса величины ajj, равны одноименному коэффициенту натурального баланса умноженному на отношение цены затрачиваемого продукта к цене производимого продукта. Это отношение называется индексом относительной ценности двух продуктов. Оно показывает во сколько раз единица затрачиваемого продукта дороже единицы производимого продукта.
Xi = Σxj + Zj;j=1,n.
При этом Zj = Zjтак как натуральные единицы измерения равны стоимостным.
Найдем производственно - эксплуатационные нужды для сводного материального баланса:
Xij = Xij*Pi, i = l,n;
![]() XllPl + X12P1 + X13Pl + X14P
XllPl + X12P1 + X13Pl + X14P
 X21P2 + X22P2 + X23P2 + X24P2
X21P2 + X22P2 + X23P2 + X24P2
![]() X31P3 + X32P3 + X33P3 + X34P3
X31P3 + X32P3 + X33P3 + X34P3
X4lP4 + X42P4 + X43P4 + X44P4

31,69*5 31,71*5 0*5 39,3*5
![]() 13,58*15 9,51*15 12,58*15 31,44*1
13,58*15 9,51*15 12,58*15 31,44*1
67,91*5 15,85*5 12,58*5 18,34*5
45,27*10 22,19*10 31,46*10 13,1*10

158.45 158,55 0 196,5
203,7 142,65188,7 471,6
339,55 79,25 62,9 91,7
452,7 221,9 314,6 131
Найдем стоимость валовой продукции (Xj)
Xi = Xi*P;
 452,708*5 2263,54
452,708*5 2263,54
317,127*15 4756,90
Xi =314,693*5 1573,46
![]() 262,041*10 2620,41
262,041*10 2620,41
Найдем стоимость конечной продукции (Yi):
Yi = Yi*Pi

350*5 1750
![]() Yi = 250*15 3750
Yi = 250*15 3750
200*5 1000
 150*10 1500
150*10 1500
На основе выше найденных данных таблица свободного материального баланса будет иметь следующий вид:
| Отрасль | А | Б | В | Г | Σ | Y | X |
| А | 158.45 | 158.55 | 0 | 196.5 | 513.5 | 1750 | 2263.54 |
| Б | 203.7 | 142.65 | 188.7 | 471.6 | 1006.65 | 3750 | 4756.90 |
| В | 339.55 | 79.25 | 69.2 | 91.7 | 573.4 | 1000 | 1573.46 |
| Г | 452.7 | 221.9 | 314.6 | 131 | 1120.2 | 1500 | 2620.41 |
| Σ | 1154.4 | 602.35 | 566.2 | 890.8 | 3213.75 | ||
| Z | 1471.29 | 3568 | 1290.36 | 1598.61 |
| ||
| X | 2263.54 | 4756.90 | 1573. 46 | 2620.41 |
| ||
3.Коэффициенты bij - элементы матрицы В и могут быть определены через коэффициенты прямых материальных затрат (аij), т.к.
В = (Еn-А)‾ 1
Для определения матрицы В обозначим (Еn - А) = С, тогда С*В = Еn
Значит, по правилам умножения (строка на столбец) матриц, получим:
![]() i=l,n; k=l,n;
i=l,n; k=l,n;
Получаем n систем уравнений, в каждом из которых п уравнений. Первая система позволяет найти компоненты первого столбца матрицы В, вторая - второго и т.д.
Найдем элементы матрицы С для заданных условий:
(Е-А) = С

 0.07 0.10 0.00 0.15 0.93 -10 0 -0.15
0.07 0.10 0.00 0.15 0.93 -10 0 -0.15
A = 0.03 0.03 0.04 0.12 C = -0.03 0.97 -0.04 -0.12
![]() 0.15 0.05 0.04 0.07 -0.15 -0.05 0.96 -0.07
0.15 0.05 0.04 0.07 -0.15 -0.05 0.96 -0.07
0.10 0.07 0.10 0.05 -0/10 -0.07 -0.10 0.95
Т.к. С*В = Еn запишем системы уравнений:
![]() 0,93b13 - 0,10b23 – 0b33 - 0,15b43 =0
0,93b13 - 0,10b23 – 0b33 - 0,15b43 =0
-0,03b13 + 0,97b23 - 0,04b33 - 0,12b43=0
-0,15b13 - 0,05b23+ 0,96b33 - 0,07b43 =1
-0,10b13 - 0,07b23 - 0,10b33 + 0,95b43 =0
![]() 0,93b14 - 0,10b24 – 0b34 - 0,15b44 =0
0,93b14 - 0,10b24 – 0b34 - 0,15b44 =0
-0,03b14 + 0,97b24 - 0,04b34- 0,12b44=0
-0,15b14 - 0,05b24+ 0,96b34 - 0,07b44 =0
-0,10b14 - 0,07b24 - 0,10b34+ 0,95b44 =1
Значение полных материальных затрат (bij) найдены по методу Гаусса.
 1,1043 0,1290,0952 0,1925
1,1043 0,1290,0952 0,1925
B= 0,0592 1,05060,0591 0,1464
0,1858 0,08221,0573 0,1183
0,1401 0,09970,1176 1,096
4. Через коэффициенты полных материальных затрат (by) и объемы конечной продукции (Y;) можно определить объемы валовой продукции (хij), используя модель объемов выпуска, которая имеет следующий вид:
X = B*Y;
Xi = Σbij*Yi
Таким образом, объемы валовой продукции будут равны:

452,73
Х= 317,15
314,68
262,02
Значения валовой продукции, полученные с помощью приближенных методов, в нашем случае и по методу простой итерации, и по методу Зейделя равны:
 452,708
452,708
X =317,127
314,693
262,041
Таким образом, расхождения результатов имеют значения:
Δx1 =-0,022
Δх2 =-0,023
Δх3 = 0,013
Δх4= 0,021
Незначительные расхождения в результатах можно объяснить тем, что при расчете были использованы разные методы. При нахождении объема валовой продукции через коэффициенты прямых материальных затрат (аij) использовались приближенные методы, где решение находится с заданной точностью Е.
При нахождении объема валовой продукции с помощью коэффициентов полных материальных затрат (bij) использовался точный метод расчета (метод Гаусса), который позволяет определить единственно точное значение.
5. Чтобы определить, как изменяются цены в отраслях при изменении удельной условно чистой продукции, применяется модель равновесных цен, которая имеет следующий вид:
Рi = Σаij*Рi + Zj j=l,n;
где zj=-Zj / Xj, и zj- удельная условно - чистая продукция j-той отрасли, приходящаяся на единицу валовой продукции этой отрасли.
Р = А’*Р + Z, (En-A’)*P = Z
Р* (En – А’)*(Еn - А’)‾1 =(Еn – A’)‾1 *Z, значит Р = (Еn – А’) ‾1 * Z, а так как
(Еn-А’) ‾1=В B'=(Еn – А’) ‾1, то Р = B’*Z -это и есть модель равновесных цен.
Матрица В’ - матричный мультипликатор ценового эффекта распространения.

1,1043 0,0592 0,1858 0,1401
В’ = 0,129 1,0506 0,0822 0,0997
0,0952 0,0591 1,0573 0,1183
0,1925 0,1464 0,1176 1,096
Найдем zj:
Z1 =1471,29/452,73= 3,2
Z2 =3568/317,15= 11,2
Z3 =1290,36/314,68=4,1
Z4 = 1598,61/262,02=6,1
Для проверки полученных значений найдем цены:
P1 = b11*Z1 + b21*Z2 + b31*Z3 + b41*Z4
P2 = b12*Z1 + b22*Z2 + b32*Z3 + b42*Z4
Рз = b13*Z1 + b23*Z2 + b33*Z3 + b43*Z4
P4 = b14*Z1 + b24*Z2 + b34*Z3 + b44*Z4, таким образом
P1= 1,1043 *3,2+0,059 *11,2+0,1858 *4,1 +0,1401*6,1 = 5
P2= 0,129*3,2+1,0506*11,2+0,0822*4,1 +0,0997*6,1 = 15
P3 = 0,0952*3,2+0,0591*11,2+1,0573*4,1 +0,1183*6,1 =5
P4= 0,1925*3,2+0,1464*11,2+0,1176*4,1 +1,096*6,1 = 10
Найдем новые цены:
Pj = 0,05bij*Zi - 0,1 bij*Z4+Рi
P1 =0,05*1,1043 *3,2-0,l*0,1401*6,l +5=5,16 ,
P2 = 0,05*0,129*3,2-0,1*0,0997*6,1 +15=14,96
P3 = 0,05*0,0952*3,2-0,1*0,1183*6,1 +5=4,95
P4= 0,05*0,1925*3,2-0,1*1,096*6,1 +10=9,36
Значения изменений получатся:
![]() P1 = 0,16
P1 = 0,16
![]() P2 = -0,04
P2 = -0,04
![]() P3 = -0,05
P3 = -0,05
![]() P4=-0,64
P4=-0,64
В процентах:
![]() Pi =
Pi = ![]() Pi/Pj*100%
Pi/Pj*100%
![]() P1 =0,16 /5* 100% = 3,2%
P1 =0,16 /5* 100% = 3,2%
![]() P2 =-0,04 /15*100% = -0,27%
P2 =-0,04 /15*100% = -0,27%
![]() P3 =-0,05 /5*100% = -1%
P3 =-0,05 /5*100% = -1%
![]() P4 = -0,64/10* 100% = -6,4%
P4 = -0,64/10* 100% = -6,4%
Из выше приведенных расчетов следует, что увеличение величины удельно условно - чистой продукции в секторе А на 5% и понижение в секторе Г на 10% привело к изменению цен во всех отраслях экономики. Наибольшее увеличение произошло в секторе А - на 3,2%, наименьшее в секторе Г на -6,4%, а в секторах Б; В и Г цены снизились на 0,04 ; 0,05 и 0,64 соответственно.
Вывод
На основе данной работы можно проследить взаимосвязи происходящих процессов в экономике и оценить влияние изменений, как на каждый отдельный сектор, так и на всю экономику в целом.
Примененный балансовый метод планирования позволяет увязать объем и структуру общественных потребностей с материальными, трудовыми, финансовыми ресурсами, а так же определить основные пропорции воспроизводства в целом в экономике, по отраслям и экономическим районам.
Таким образом, следует сказать, что межотраслевой баланс -это основа прогнозирования развития экономики.