Методи економетрії
Міністерство освіти і науки України
Відкритий міжнародний університет розвитку людини "Україна"
Самостійна робота на тему:
Економетричний аналіз даних
виконала
студентка групи ЗМЗЕД-41
спеціальності ”менеджмент
зовнішньекономічної діяльності”
Викладач: Пономаренко І.В.
Київ-2006
Мета роботи:
за даними спостережень необхідно:
1.провести розрахунки параметрів чотирьохфакторної моделі;
2.обчислити розрахункові значення Yр за умови варыювання пояснюючих змынних х.
3.перевырити істотність моделі за допомогою коефіцієнтів кореляції і детермінації, критерію Фішера та критерію Стюдента.
4.перевірити наявність мультиколінеарності за допомогою алгоритму Фаррара-Глобера.
Хід роботи:
1.1 проведення розрахунків параметрів чотирьохфакторної моделі
а) запишемо матрицю пояснбвальних змінних, яка буде містити: перший стовпчик – одиничні значення; наступні стопчики значення х1, х2, х3, х4 – відповідно інвестиції, виробничі фонди, продуктивність праці та оборотність коштів.
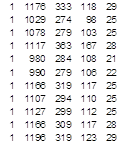
Х=
б) транспонуємо матрицю Х:
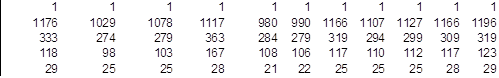
ХI=
в) виконуємо множення матриць ХХI в результаті отримуємо:
| 11 | 12132 | 3352 | 1279 | 282 |
| 12132 | 13437196 | 3710520 | 1415909 | 312747 |
| 3352 | 3710520 | 1028912 | 394291 | 86451 |
| 1279 | 1415909 | 394291 | 152077 | 33041 |
| 282 | 312747 | 86451 | 33041 | 7300 |
г) знайдемо матрицю обернену до ХХI:
| 27,6707 | -0,0271 | -0,0547 | 0,0401 | 0,5579 |
| -0,0271 | 0,0001 | -0,0003 | 0,0003 | -0,0018 |
| -0,0547 | -0,0003 | 0,0021 | -0,0024 | -0,0001 |
| 0,0401 | 0,0003 | -0,0024 | 0,0032 | -0,0020 |
| 0,5579 | -0,0018 | -0,0001 | -0,0020 | 0,0663 |
д) помножимо ХIY:
| 7135 |
| 7902232 |
| 2187659 |
| 836936 |
| 184100 |
є)отримаємо параметри розрахувавши вектор ^A=(ХХI)-1 ХIY
| -24,4079 |
| 0,1725 |
| 1,4300 |
| -0,2449 |
| 2,9469 |
Після проведення розрахунків було отримано наступні значення параметрів лінійної моделі:
b0 =-24,41
b1 =0,1725
b2 =1,43
b3 =-0,2449
b4 =2,9469
На основі отриманих параметрів чоритьхфакторної лінійної моделі побудуємо рівняння, яке буде мати наступний вигляд:
Yр = (-24,41)+0,1725х1+1,43х2-0,2449х3+2,9469х4.
Отже, отримане рівняня свідчить, що при збільшенні інвестицій на одиницю, прибутки зростуть 172 у.о, за умови незмінності інших факторів; при збільшенні виробничих фондів на одиницю прибутки зростуть на 1430 у.о. за умови незмінності інших факторів; при збіленні продуктивності праці на одиницю прибутки зменьшаться на 244 у.о. за умови незмінності інших факторів; при збільшенні оборотності коштів на одиницю, прибутки збільшаться на 2946 у.о.
1.2 обчислення розрахунків значень Yр за умови варіювання
Вплив факторів на прибуток
| № | Yp | Yp(x1) | Yp(x2) | Yp(x3) | Yp(x4) |
| 1 | 749,43 | 701,88 | 728,53 | 688,84 | 689,33 |
| 2 | 634,66 | 676,60 | 645,93 | 693,74 | 686,38 |
| 3 | 648,86 | 685,03 | 652,93 | 692,51 | 686,38 |
| 4 | 766,33 | 691,73 | 770,53 | 676,83 | 695,22 |
| 5 | 626,00 | 668,17 | 659,93 | 691,29 | 674,59 |
| 6 | 624,15 | 669,89 | 652,93 | 691,78 | 677,54 |
| 7 | 716,57 | 700,16 | 708,93 | 689,08 | 686,38 |
| 8 | 673,14 | 690,01 | 673,93 | 690,80 | 686,38 |
| 9 | 683,09 | 693,45 | 680,93 | 690,31 | 686,38 |
| 10 | 711,41 | 700,16 | 694,93 | 689,08 | 695,22 |
| 11 | 732,05 | 705,32 | 708,93 | 687,61 | 698,17 |
cер варт | 687,79 | 689,31 | 688,94 | 689,26 | 687,45 |
1.3 перевірити істотність моделі за допомогою коефіціентів кореляції і детермінації
Для перевірки істотності моделі за допомогою коефіцієнтів кореляції, для цього необхідно побудувати кореляційну матрицю.
| Х1 | Х2 | Х3 | Х4 | Y | |
| Х1 | 1 | 0,2393 | 0,3829 | 0,8633 | -0,170 |
| Х2 | 0,239 | 1 | 0,3291 | 0,259 | -0,218 |
| Х3 | 0,383 | 0,3291 | 1 | 0,5175 | 0,214 |
| Х4 | 0,863 | 0,259 | 0,5175 | 1 | 0,326 |
| Y | -0,170 | -0,2180 | 0,2140 | 0,3263 | 1 |
Отже, найбільший коефіціент кореляції між пояснювальними змінними спостерігається для х4та х3:R(х4, х3) = 0,5175. В той же час, найбільший коефіціент кореляції між пояснюваною змінними спостерігається для х1та х4 :R(х1, х4) = 0,863. Отриманий результат показав, що оборотність коштів найбільше пов’язана з інвестиціями.
Наступним кроком перевірки істотності зв’язку між змінними буде розрахунок коефіцієнта детермінації з використанням середніх квадратів відхилень:
R2 = (Q2y - Q2u)/ Q2y=1-(Q2u - Q2y).
Виходячи з формули розраховуємо загальну дисперсію (Q2y) та дисперсію залишків (Q2u).
а) загальна дисперсія (для прибутку) розраховуються на основі розрахункової таблиці:
| 706 | 57,36364 | 3290,58678 |
| 588 | -60,63636 | 3676,76860 |
| 617 | -31,63636 | 1000,85950 |
| 725 | 76,36364 | 5831,40496 |
| 598 | -50,63636 | 2564,04132 |
| 588 | -60,63636 | 3676,76860 |
| 686 | 37,36364 | 1396,04132 |
| 608 | -40,63636 | 1651,31405 |
| 627 | -21,63636 | 468,13223 |
| 686 | 37,36364 | 1396,04132 |
| 706 | 57,36364 | 3290,58678 |
| 648,6364 | x | 2567,5041 |
Q2u= 2567,5041/11 = 233,409
б) дисперсія залишків розраховуються за допомогою наступного співвідношення:
Q2u=YIY-^AХIY/-m
· спочатку множимо YIна матрицю Y:
![]() YI=
YI=
YIY =| 4649403 |
· транспонуємо матрицю ^A:
| -24,411 | 0,173 | 1,430 | -0,245 | 2,947 |
A=
· проводимо розрахунок^AХIY:
AХIY = | 4654875 |
· скориставшись співвідношенням, знаходимо дисперсію залишків:
Q2u=4649403-4654875/11-4=-501,461
· розраховуємо коефіцієнт детермінації:
R2 = 1-(-501,461/233,409) = 3,148
Розрахований коефіцієнт детермінації R2 = 3,148, дана чотирьох факторна модель показує, що прибуток повністю визначається врахованими факторами.
1.4 перевірити нявність мультиколінеарності за допомогою алгоритму Фаррара-Глобера
1.4.1 нормалізуємо зміни в економетричній моделі
| № | Xі1-Х1 | Xі2-Х2 | Xі3-Х3 | Xі4-Х4 | (Xі1-Х1)2 | (Xі2-Х2)2 | (Xі3-Х3)2 | (Xі4-Х4)2 |
| 1 | -73 | -28 | -2 | -3 | 5342 | 799 | 2,98347 | 11,314 |
| 2 | 74 | 31 | 18 | 1 | 5463 | 944 | 333,893 | 0,40496 |
| 3 | 25 | 26 | 13 | 1 | 620 | 662 | 176,165 | 0,40496 |
| 4 | -14 | -58 | -51 | -2 | 199 | 3396 | 2573,26 | 5,58678 |
| 5 | 123 | 21 | 8 | 5 | 15107 | 430 | 68,438 | 21,4959 |
| 6 | 113 | 26 | 10 | 4 | 12748 | 662 | 105,529 | 13,2231 |
| 7 | -63 | -14 | -1 | 1 | 3980 | 204 | 0,52893 | 0,40496 |
| 8 | -4 | 11 | 6 | 1 | 17 | 115 | 39,3471 | 0,40496 |
| 9 | -24 | 6 | 4 | 1 | 580 | 33 | 18,2562 | 0,40496 |
| 10 | -63 | -4 | -1 | -2 | 3980 | 18 | 0,52893 | 5,58678 |
| 11 | -93 | -14 | -7 | -3 | 8666 | 204 | 45,2562 | 11,314 |
| Всьго | х | х | х | х | 56703 | 7466 | 3364,18 | 70,5455 |
Q2X1= | 5154,82 |
Q2X2= | 678,744 |
Q2X3= | 305,835 |
Q2X4= | 6,413 |
1.4.2 нормалізуємо зміни в економетричній моделі. Матриця нормалізованих змінних буде мати наступний вигляд
| -0,31 | -0,1187 | -0,0298 | -0,4005 |
| 0,3104 | 0,1290 | 0,3150 | 0,0758 |
| 0,1046 | 0,1080 | 0,2288 | 0,0758 |
| -0,0592 | -0,2447 | -0,8746 | -0,2814 |
| 0,5162 | 0,0870 | 0,1426 | 0,5520 |
| 0,4742 | 0,1080 | 0,1771 | 0,4329 |
| -0,2649 | -0,0599 | -0,0125 | 0,0758 |
| -0,0172 | 0,0450 | 0,1081 | 0,0758 |
| -0,1012 | 0,0241 | 0,0737 | 0,0758 |
| -0,2649 | -0,0179 | -0,0125 | -0,2814 |
| -0,3909 | -0,0599 | -0,1160 | -0,4005 |
Х* =
1.4.3 визначаємо кореляційну матрицю на основі елементів матриці нормалізованих змінних
Rхх= Х*I Х*
| 1 | 0,2393 | 0,3829 | 0,8633 |
| 0,239 | 1 | 0,3291 | 0,259 |
| 0,383 | 0,3291 | 1 | 0,5175 |
| 0,863 | 0,259 | 0,5175 | 1 |
Rхх=
Обчислимо Х2 занаступною формулою:
Х2=-(-1-1/6(2m+5))ln | Rхх |.
· розраховуємо визначник кореляційної матриці скориставшись правилом Сарруса:
|Rхх | =1*1*1*1-0,863*0,3291*0,863*0,3291 = 0,9193.
Знаходимо Х2:
Х2=-(11-1-1/6(2*4+5))ln | 0,9193|=7,8342*-0,08=-0,63.
З ймовірністю 0,919 можна стверджувати, що між факторними ознаками не існує мультиколінеарності, оскільки Х факт. < Х табл.