Расчет и конструирование балочной клетки

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Тверской государственный технический университет

Кафедра «Конструкции и сооружения»

Курсовая работа

По дисциплине «Металлические конструкции»

На тему: «Расчет и конструирование балочной клетки»

Выполнил

студент ИДПО

группы ПГС-30-08

Принял: Горшков А.В

Тверь 2011г.

Исходные данные

При нормальном типе балочной клетки нагрузки от настила покрытия передаются на балки настила, которые опираются на главные балки. Шаг главных балок равен пролету балок настила. Все несущие элементы балочной клетки имеют сопряжение в одном уровне.

Марка стали для балок настила и главных балок С275 с расчетным сопротивлением R_y=2750 кгс/см², для колонн С235 с расчетным сопротивлением R_y=2350 кгс/см².

По таблице 55* СНиП ∥-23-81* «Стальные конструкции» выбираем сварку: принимаем электрод Э42 по ГОСТ 9467-75*, сварочную проволоку Св-08А по ГОСТ 2246-70* и флюс АН-348-А по ГОСТ 9087-81*.

По таблице 61* СНиП ∥-23-81* «Стальные конструкции» подбираем высокопрочные болты диаметром 24 мм, морка стали по ГОСТ 4543-77* 40Х «селект», R_bun=11500 кгс/см².

1. Выбор схемы балочной клетки и подбор сечения балок настила и вспомогательных балок (усложненная компоновка)

1.1 Вариант 1 – пролет балки настила 8 м, шаг балок 2 м

Рис. 1

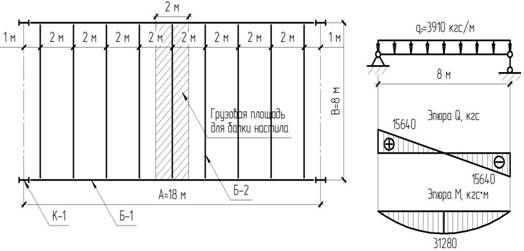
Принимаем железобетонный настил толщиной tн=0.1 м и плотностью железобетона ρ=2500 кг/.

Временная нагрузка задана

Нагрузка от собственного веса железобетонного настила составит:

Выделяем грузовую площадь на 1 балку настила (рис. 1).

Нормативное значение нагрузки, действующей на балку настила

Где a – шаг балок настила;

B – пролет балки настила.

Расчетное значение нагрузки, действующей на балку настила

;

Где  и  - коэффициенты надежности по нагрузке для временной нагрузки и железобетонного настила (СНиП 2.01.07-85*).

Максимальный изгибающий момент равен

Максимальная поперечная сила

Расчет на прочность разрезных балок сплошного сечения из стали с пределом текучести до 5400 кгс/см², несущих статическую нагрузку, при изгибе в одной из главных плоскостей выполняют по формуле

Где с1 – коэффициент, учитывающий развитие пластических деформаций в элементах конструкций и зависящий от формы сечения;

 - расчетное сопротивление балки по пределу текучести;

 – коэффициент условий работы для сплошных прокатных балок, несущих статическую нагрузку (СП 53-102-2004 табл. 1).

Требуемый момент сопротивления поперечного сечения балки равен

По сортаменту прокатных профилей (СТО АСЧМ 20-93) выбираем двутавр № 45 со следующими геометрическими характеристиками

Wx=1231 см³;

Ix=27696 см⁴;

Sx=708 см³;

Р=66.5 кг/м;

d=0.9 см;

b=16 см;

h=45 см.

Значения касательных напряжений в сечении изгибаемого элемента должны удовлетворять условию

Rs – расчетное сопротивление стали сдвигу Rs=0.58∙Ry=0.58∙2750=1595 кгс/см² (СП 53-102-2004 табл. 2);

где Sx – статический момент сдвигаемой части сечения относительно нейтральной оси;

Ix – момент инерции кручения балки (Ix= Sx∙h∙d);

d – толщина стенки балки.

Условие выполняется, следовательно опорные сечения балок настила удовлетворяют условию прочности по касательным напряжениям.

Расчет по 2 группе предельных состояний для изгибаемых элементов заключается в определении вертикального относительного прогиба и сравнение его с нормируемым.

Относительный прогиб однопролетной балки, нагруженной равномерно распределенной нагрузкой

По таблице 19 СНиП 2.01.07-85* в зависимости от пролета определяем нормируемый прогиб. Для пролета l=8м:

Условие выполняется, то есть сечение балки настила удовлетворяет требованиям жесткости.

Подсчитаем расход и стоимость материалов при первом варианте компоновки балочной клетки.

Расход металла на 1 м²:

Расход железобетона 1 м²∙0.1 м=0.1 м³.

Стоимость 1 м² настила: С=0.03325 т∙10000 р+0.1 м³∙1000=432.5 р.

1.2 Вариант 2 - пролет балки настила 8 м, шаг балок 1.5 м

Рис. 2

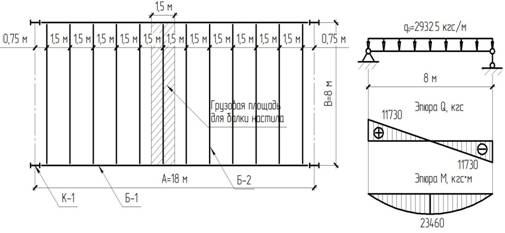
Принимаем железобетонный настил толщиной tн=0.1 м и плотностью железобетона ρ=2500 кг/.

Временная нагрузка задана

Нагрузка от собственного веса железобетонного настила составит

Выделяем грузовую площадь на 1 балку настила (рис. 2).

Нормативное значение нагрузки, действующей на балку настила

Расчетное значение нагрузки, действующей на балку настила

Максимальный изгибающий момент равен

Максимальная поперечная сила

Требуемый момент сопротивления поперечного сечения балки равен

По сортаменту прокатных профилей (СТО АСЧМ 20-93) выбираем двутавр № 40 со следующими геометрическими характеристиками

Wx=953 см³;

Ix=19062 см⁴;

Sx=545 см³;

Р=57 кг/м;

d=0.83 см;

b=15.5 см;

h=40 см.

Значения касательных напряжений в сечении изгибаемого элемента должны удовлетворять условию

Условие выполняется, следовательно опорные сечения балок настила удовлетворяют условию прочности по касательным напряжениям.

Расчет по 2 группе предельных состояний для изгибаемых элементов заключается в определении вертикального относительного прогиба и сравнение его с нормируемым.

Относительный прогиб однопролетной балки, нагруженной равномерно распределенной нагрузкой

По таблице 19 СНиП 2.01.07-85* в зависимости от пролета определяем нормируемый прогиб. Для пролета l=8м

Условие выполняется, то есть сечение балки настила удовлетворяет требованиям жесткости.

Подсчитаем расход и стоимость материалов при втором варианте компоновки балочной клетки.

Расход металла на 1 м²

Расход железобетона 1 м²∙0.1 м=0.1 м³.

Стоимость 1 м² настила: С=0.038 т∙10000 р+0.1 м³∙1000=480 р

1.3 Вариант 3 (усложненная компоновка) – пролет балок настила 3 м, шаг балок настила 1.6 м, пролет вспомогательных балок 8 м, шаг вспомогательных балок 3 м

Рис. 3

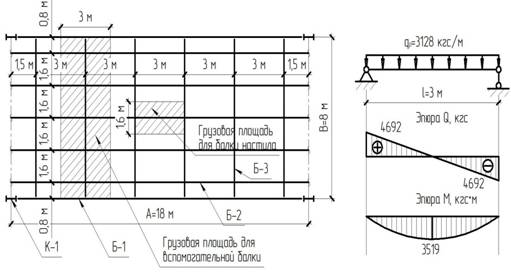
Расчет балки настила.

Принимаем железобетонный настил толщиной tн=0.1 м и плотностью железобетона

ρ=2500 кг/

Временная нагрузка задана

Нагрузка от собственного веса железобетонного настила составит

Выделяем грузовую площадь на 1 балку настила (рис. 3).

Нормативное значение нагрузки, действующей на балку настила

Расчетное значение нагрузки, действующей на балку настила

Максимальный изгибающий момент равен

Максимальная поперечная сила

Требуемый момент сопротивления поперечного сечения балки равен

По сортаменту прокатных профилей (СТО АСЧМ 20-93) выбираем двутавр № 18 со следующими геометрическими характеристиками:

Wx=143 см³;

Ix=1290 см⁴;

Sx=81.4 см³;

Р=18.4 кг/м;

d=0.51 см;

b=9 см;

h=18 см.

Значения касательных напряжений в сечении изгибаемого элемента должны удовлетворять условию

Условие выполняется, следовательно опорные сечения балок настила удовлетворяют условию прочности по касательным напряжениям.

Расчет по 2 группе предельных состояний для изгибаемых элементов заключается в определении вертикального относительного прогиба и сравнение его с нормируемым.

Относительный прогиб однопролетной балки, нагруженной равномерно распределенной нагрузкой

По таблице 19 СНиП 2.01.07-85* в зависимости от пролета определяем нормируемый прогиб. Для пролета l=3м

Условие выполняется, то есть сечение балки настила удовлетворяет требованиям жесткости.

Расчет вспомогательной балки.

Рис. 4

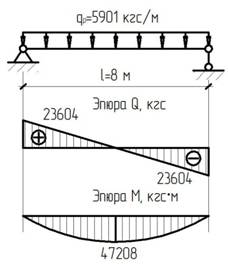
Временная нагрузка задана

Нагрузка от собственного веса железобетонного настила составит

Нагрузка от балок настила

где А – шаг колонн в продольном направлении;

В – шаг колонн в поперечном направлении;

Р – нагрузка от 1 м балки настила.

Выделяем грузовую площадь на 1 вспомогательную балку (рис. 3).

Нормативное значение нагрузки, действующей на балку настила

Расчетное значение нагрузки, действующей на балку настила

Где  - коэффициент надежности по нагрузке для металлических конструкций (СНиП 2.01.07-85*).

Максимальный изгибающий момент равен

Максимальная поперечная сила

Требуемый момент сопротивления поперечного сечения балки равен

По сортаменту прокатных профилей (СТО АСЧМ 20-93) выбираем двутавр № 50 со следующими геометрическими характеристиками

Wx=1598 см³;

Ix=39727 см⁴;

Sx=919 см³;

Р=78.5 кг/м;

d=1 см;

b=17 см;

h=50 см.

Значения касательных напряжений в сечении изгибаемого элемента должны удовлетворять условию

Условие выполняется, следовательно опорные сечения балок настила удовлетворяют условию прочности по касательным напряжениям.

Расчет по 2 группе предельных состояний для изгибаемых элементов заключается в определении вертикального относительного прогиба и сравнение его с нормируемым.

Относительный прогиб однопролетной балки, нагруженной равномерно распределенной нагрузкой

По таблице 19 СНиП 2.01.07-85* в зависимости от пролета определяем нормируемый прогиб. Для пролета l=8м

Условие выполняется, то есть сечение балки настила удовлетворяет требованиям жесткости.

Подсчитаем расход и стоимость материалов при третьем варианте компоновки балочной клетки.

Расход металла на 1 м²

Где Р1 и Р2 – вес 1 метра профиля балки настила и вспомогательной балки.

Расход железобетона 1 м²∙0.1 м=0.1 м³.

Стоимость 1 м² настила: С=0.0377 т∙10000 р+0.1 м³∙1000=477 р.

Таким образом наиболее экономичным является 1 вариант компоновки балочной клетки.

2. Расчет и конструирование главной балки

Балки настила опираются на главные балки равномерно с шагом 2 метра, пролет главных балок составляет 18 м. Таким образом, на главную балку будут действовать 9 сосредоточенных сил, примем их как равномерно распределенную нагрузку.

Рис. 5

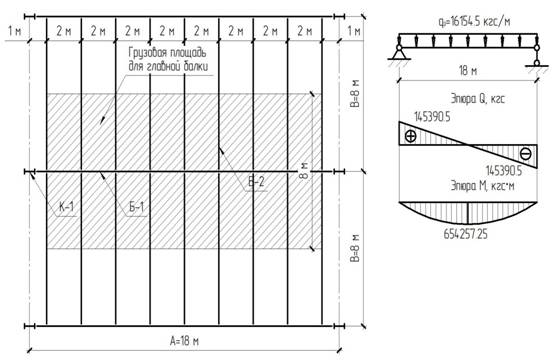
Нагрузка, действующая на главную балку будет включать в себя:

· Полезную нагрузку;

· Собственный вес настила;

· Собственный вес балок настила;

· Собственный вес главной балки (1-2 % от нагрузки на нее).

Нагрузка от балок настила

Вес главной балки

Нормативное значение нагрузки, действующей на главную балку

Расчетное значение нагрузки, действующей на главную балку

Максимальный изгибающий момент равен

Максимальная поперечная сила

Внутренние усилия, возникающие в главной балке настолько значительны, что использование прокатных профилей исключено. Поэтому главная балка проектируется составной. Как правило, составные балки проектируются сварными, а их сечение напоминает сечение прокатных двутавров: один вертикальный лист стали образует стенку двутавра, два горизонтальных листа образуют его полки.

2.1 Определение размеров сечения

Главная балка проектируется переменного по длине сечения. Определяющим в компоновке сечения главной балки является подбор размеров стенки балки – высоты и толщины. Высота главной балки, основную часть которой составляет высота стенки, определяется по экономическим соображениям, жесткости балки и допустимой строительной высоте конструкции перекрытия. Каждый из перечисленных факторов определяет оптимальное, минимальное и максимальное значение высоты балки. Толщина стенки балки также определяется несколькими факторами и соответственно имеет несколько значений – минимальное и, принимаемое из условия работы главной балки на касательные напряжения, и рациональное, принимаемое из экономических соображений. Минимальная высота стенки главной балки определяется из условия жесткости балки с использованием формулы, связующей момент сопротивления сечения W и момент инерции I

Где y – расстояние от нейтральной оси сечения до крайнего волокна.

Поскольку определяется минимальное значение высоты, используется минимальное значение y

где  - минимальный требуемый момент инерции всего сечения главной балки;

W_{n, min} – минимальный требуемый момент сопротивления всего сечения главной балки.

Минимальный момент сопротивления сечения главной балки определяется из условия прочности изгибаемых элементов в соответствии с требованиями п. 5.12 СНиП ∥-23-81* «Стальные конструкции»

Минимальный момент инерции сечения главной балки определяется из условия жесткости в соответствии с требованием обеспечения допустимого относительного прогиба балки, который для главных балок рабочих площадок производственных зданий при отсутствии крановых путей составляет:  (Беленя Е.И. Металлические конструкции, табл. 3.3).

Минимальное значение высоты главной балки

Оптимальная высота стенки балки определяется, исходя из соображений минимизации массы балки. Формула для определения высоты стенки главной балки при минимуме массы балки имеет следующий вид

где К – коэффициент, зависящий от конструктивного оформления балки, для сварных балок К=1.15;

Предварительно определяем высоту стенки

 – толщина стенки, ориентировочно принимаем .

где λw=150 – условная гибкость стенки (Беленя Е.И. Металлические конструкции, табл. 7.2).

Максимальная высота стенки главной балки

Где Нстр – строительная высота;

tп – высота перекрытия.

Высота балки должна вписываться в заданные габариты и быть кратной модулю унификации 100 мм. Принимаем высоту балки hw=180 см.

Минимальная толщина стенки главной балки определяется из условия ее прочности при работе на срез с использованием формулы

Где Rs=0.58∙Ry=0.58∙2750=1595 кгс/см² (СП 53-102-2004 табл. 2);

h – принятая высота балки.

Минимальную толщину стенки, необходимую для обеспечения местной устойчивости главной балки без постановки продольного ребра жесткости определим по формуле

Таким образом, согласно ГОСТ 19903-74*, принимаем толщину стенки .

Проверим условную гибкость стенки главной балки

Данное значение попадает в диапазон 3.5≤λw≤6, что говорит о выполнении условия.

Толщину листа полки главной балки принимаем .

Полная высота главной балки будет равна

.

Ширину листа главной балки определяем из требуемого значения площади сечения полки. Формулу для определения площади сечения одной полки получим из формулы Штейнера, которая позволяет определять моменты инерции сложных сечений относительно осей, не совпадающих с нейтральной осью всего сечения. Ввиду малости значения моментом инерции сечения полки относительно собственной оси можно предебречь, тогда формула для определения площади сечения одной полки примет вид

Где  – требуемый момент инерции одной полки относительно нейтральной оси балки;

 – площадь сечения одной полки;

h₀ – расстояние между собственными осями полок.

Требуемый момент инерции сечения главной балки

Требуемый момент инерции стенки главной балки

Требуемый момент инерции поясов главной балки

Требуемая площадь сечения поясов балки

Где h₀=h_w+t_f=180+2=182 см

Ширину полки главной балки принимаем по действующему сортаменту листовой стали (ГОСТ 19903-74*) с учетом принятой толщины листа и назначается не менее требуемой по площади сечения полки

Ширину полки принимают в диапазоне  высоты балки, так как при  будет существенно проявляться неравномерность распределения напряжений по ширине пояса, а при  мала боковая жесткость балки, что ухудшает условия монтажа и общую устойчивость балки.

По ГОСТ 82-70 принимаем листы 20*450 мм. . Условие выполняется.

Площадь сечения полки А_f=2∙45=90 см².

Исходя из требований местной устойчивости, отношение неокаймленного свеса пояса  к его толщине  ограничивается при работе балки в пределах упругих деформаций условием

А при развитии пластических деформаций условием

Местная устойчивость пояса обеспечена.

Определим геометрические характеристики сечения главной балки

Проверка сечения на прочность

Недонапряжение составит

Условие выполняется, следовательно сечение главной балки удовлетворяет условиям проверки по нормальным напряжениям.

2.2 Изменение сечения балки по длине

Изменение сечения главной балки по длине производим из экономических соображений, связанных с тем, что значения моментов, по которым производится расчет сечения, действуют лишь в середине пролета. Изменить сечение балки можно, уменьшив высоту или толщину стенки, ширину или толщину полки. В сварных балках наиболее распространено уменьшение ширины полки, при этом остаются постоянными высота и толщина стенки и толщина полки, что удобно при выполнении сварки поясных листов друг с другом. Наиболее выгодное по расходу стали место изменения сечения поясов однопролетной сварной балки находится на расстоянии 1/6 пролета балки от опоры.

Усилия в сечении, расположенном на расстоянии 3 м от опоры находятся по формулам

Площадь уменьшенного сечения пояса принимается из условия прочности на растяжение сварного шва, стыкующего различные сечения пояса. В таком случае стык растянутого пояса главной балки выполняют прямым с ручной сваркой без физического контроля качества.

М1 – изгибающий момент в месте изменения сечения главной балки;

 - требуемый момент сопротивления измененного сечения главной балки;

 - расчетное сопротивление сварного стыкового шва по пределу текучести с физическим контролем качества (СП 53-102-2004 табл. 4).

Определим требуемые момент сопротивления и площадь пояса

При этом ширина пояса должна отвечать следующим требованиям

Окончательно принимаем пояс 240*20 мм по ГОСТ 82-70. Так как мы увеличили ширину поясов, место изменения сечения поясов можно передвинуть дальше 1/6 пролета. Находим эту точку в обратной последовательности

Принимаем Х=3.5 м.

Находим геометрические характеристики измененного сечения:

Статический момент полусечения балки

2.3 Проверку прочности по касательным напряжениям элементов, изгибаемых в одной из главных плоскостей, выполняем по формуле

Условия выполняются, следовательно, прочность балки по нормальным и касательным напряжениям обеспечена.

Для стенки балки должно выполняться условие

Где σ – нормальное напряжение в серединной плоскости стенки;

τ – касательное напряжение, воспринимаемое стенкой.

Условие выполняется, следовательно, прочность балки обеспечена.

2.4 Проверка общей устойчивости

Проверку общей устойчивости можно не проводить при  и  при соблюдении условия

Где l0 – расстояние между осями балок настила, h0 – расстояние между осями поясных листов,  так как τ=0 и с1=с.

В измененном сечении

δ=1 так как балка работает упруго.

Условия соблюдаются, поэтому проверку не проводим.

2.5 Проверка местной устойчивости стенки

Проверка и обеспечение местной устойчивости стенки главной балки выполняется в зависимости от значения условной гибкости стенки, которая определяется по следующей формуле

балка настил стенка сечение расчет

Значение условной гибкости стенки превышает 3.2, поэтому следует укреплять ее поперечными ребрами жесткости. Расстояние между основными поперечными ребрами жесткости при

а≤2∙h_w=2∙180=360 см

Таким образом можно расположить поперечные ребра жесткости под каждой балкой настила, которые будут на них опираться.

Местную устойчивость стенки проверяем на расстоянии а1= 1м/2=0.5 м. Определяем усилия в данном сечении

Расчет на устойчивость стенок балкок симметричного сечения, укрепленных только поперечными основными ребрами жесткости, при отсутствии местного напряжения σloc=0 и условной гибкости стенки  следует выполнять по формуле

Где σ и τ – фактические значения нормального и касательного напряжения;

σ_кр и τ_кр – критические значения нормального и касательного напряжения.

Где μ – отношение большей стороны пластинки к меньшей.

с_cr принимается по табл. 21 СНиП ∥-23-81* «Стальные конструкции» в зависимости от значения коэффициента δ, рассчитываемого по формуле

Где β – коэффициент (по табл. 22 СНиП ∥-23-81* «Стальные конструкции»)

При δ=0.49, с_cr=30

Условие соблюдается.

Местную устойчивость стенки проверяем на расстоянии а2= 1м+h_w/2=1.9 м. Определяем усилия в данном сечении

с_cr принимается по табл. 21 СНиП ∥-23-81* «Стальные конструкции» в зависимости от значения коэффициента δ, рассчитываемого по формуле

При δ=0.49, с_cr=30

Условие соблюдается.

2.6 Размеры ребер жесткости

Укрепляем стенку парными симметричными ребрами. Ширина выступающей части ребра

Толщина ребра

Принимаем t_h=8 мм.

2.7 Расчет поясных швов

Соединение поясных листов главной балки со стенкой осуществляется поясными швами. При изгибе балки это соединение предотвращает сдвиг поясов относительно стенки балки, который имел бы место при раздельной самостоятельной работе элементов балки на изгиб. Расчет соединений ведется на силу сдвига пояса относительно стенки. В сварных балках сдвигающая сила Т, приходящаяся на 1 см длины балки, определяется через касательные напряжения

Где S_f1 – статический момент пояса относительно нейтральной оси.

Сварные швы, соединяющие стенки и пояса составных двутавров балок, следует рассчитывать согласно табл. 37 СНиП ∥-23-81* «Стальные конструкции». В случае неподвижной нагрузки двусторонние угловые швы рассчитываются по формулам

Где γ_wf и γ_wz – коэффициенты условий работы шва равные 1;

b_f и b_z – коэффициенты глубины проплавления угловых швов, принимаемые при сварке элементов из стали: с пределом текучести до 530 МПа (5400 кгс/см²) – по табл. 34 СНиП ∥-23-81* «Стальные конструкции»;

R_wf и R_wz – расчетное сопротивление по условному срезу шва и по срезу металла на границе сплавления шва (табл. Г2 СП 53-102-2004»)

Отсюда получим:

- Высота катета шва из условия прочности металла шва

Высота катета шва из условия прочности металла на границе сплавления

В соответствии с конструктивными требованиями к сварным соединениям катеты угловых швов следует принимать по расчету, но не менее указанных в табл. 38 СНиП ∥-23-81* «Стальные конструкции», поэтому принимаем значение к_f=6 мм как минимально допустимое при толщине пояса t_f=17-22 мм, что больше получившегося по расчету к_f=1.8 мм.

2.8 Расчет опорного ребра

При высоте выступающей части опорного ребра а≤1.5t напряжение в нижних торцах при действии опорной реакции не должно превышать расчетного сопротивления смятию.

Где R_un – нормативное сопротивление;

γ_m – коэффициент надежности по материалу.

Из условия смятия определяется необходимая площадь поперечного сечения опорного ребра. Принимаем а≤1.5∙t=1.5∙1.6=2.4 см. Принимаем а=2 см. Требуемая площадь поперечного сечения опорного ребра равна

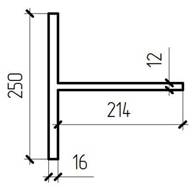
Принимаем ребро 250*16 мм. А=25∙1.6=40 см²˃А_тр=39.2 см².

Участок стенки балки составного сечения над опорой при укреплении его ребрами жесткости следует рассчитывать на продольный изгиб из плоскости как стойку, нагруженную опорной реакцией. В расчетное сечение этой стойки следует включать сечение опорного ребра и полосу стенки шириной  с каждой стороны ребра. Расчетную длину стойки следует принимать равной высоте стенки.

Расчет на устойчивость

Где φ – коэффициент продольного изгиба, определяемый по табл. 72 СНиП ∥-23-81* «Стальные конструкции», в зависимости от гибкости λ.

Где l_ef – расчетная длина стойки;

I_x – радиус инерции сечения.

Геометрические характеристики сечения, рассчитываемого на продольный изгиб, определяются для полосы стенки шириной

Определим геометрические характеристики сечения:

Рис. 6

За расчетную длину l_ef=180см принимается высота стенки на опоре. Гибкость будет равна

Для λ=31.91 и R_y=2750 кгс/см² коэффициент продольного изгиба φ=0.916.

Условие выполняется, т.е. устойчивость участка стенки главной балки над опорой обеспечена. Рассчитываем прикрепление опорного ребра к стенке балки двусторонними швами с помощью полуавтоматической сварки проволокой Св-08А по формуле. Предварительно находим параметры сварных швов и определяем минимальное значение β∙R_у:

R_wf=1800 кгс/см²;

R_wz=1650 кгс/см²;

β_f=0.9;

β_z=1.05;

Определяем катет сварных швов по формуле

Принимаем значение катета сварного шва к_f=8 мм, что больше к_f,min=6 мм.

Проверяем длину расчетной части шва

Ребро привариваем к стенке по всей высоте сплошными швами.

2.9 Расчет монтажного стыка

Монтажные стыки выполняются при монтаже на строительной площадке, они необходимы тогда, когда масса или размеры балки не позволяют перевести и смонтировать ее целиком. Расположение их должно предусматривать членение балки на отдельные отправочные элементы, по возможности одинаковые, удовлетворяющие требованиям транспортирования и монтажа наиболее распространенными средствами. Монтажный стык должен быть удален от места передачи сосредоточенных нагрузок. В соответствие с перечисленными выше требованиями выполним монтажный стык главной балки на расстоянии 8 м от опоры.

Определяем внутренние усилия на расстоянии 8 м от опоры

Изгибающий момент, воспринимаемый стенкой главной балки:

Где I_w – момент инерции стенки главной балки;

I_x – момент инерции всего сечения главной балки.

Усилие, воспринимаемое поясом главной балки

Сварной стык.

Поскольку при монтаже автоматическая сварка и сложные способы контроля затруднены, пояса свариваются косым швом, угол наклона оси шва к оси пояса φ=30⁰. Расчет сварных стыковых соединений на центральное растяжение или сжатие

Где t – наименьшая толщина соединяемых элементов; l_w – расчетная длина шва, определяемая с учетом применения обычных способов контроля качества шва.

R_wy – расчетное сопротивление по пределу текучести стыкового сварного шва

Условие не выполняется, прочность сварного монтажного стыка пояса главной балки не обеспечена. Необходимо либо увеличить длину шва, либо рассчитать болтовой стык.

Болтовой стык пояса.

Для расчета принимаем следующее соединение: стык поясов перекрывается тремя накладками – одной сверху сечением 45*2 см и двумя снизу сечением 18*2 см, в качестве болтов используются высокопрочные болты диаметром d=24 мм (А_bn=3.52 см²). Перед постановкой накладок поверхности соединяемых элементов обрабатываются дробеструйным аппаратом.

Рис. 7

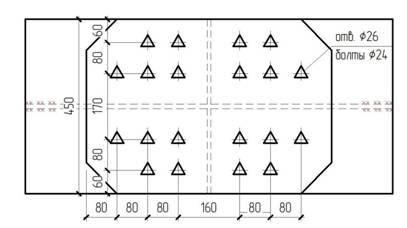
Расчетное усилие, которое может быть воспринято каждой поверхностью трения соединяемых элементов, стянутых одним высокопрочным болтом, следует определять по формуле

Где R_bh=0.7R_bun=0.7∙11000=7700 кгс/см² – расчетное сопротивление высокопрочного болта растяжению;

γ_b – коэффициент условий работы соединения, зависящий от количества болтов, необходимых для восприятия расчетного усилия γ_b=0.9 при 5≤n≤10;

А_bn – площадь сечения болта нетто, определяемая по табл. 62 СНиП ∥-23-81* «Стальные конструкции»;

Μ и γ_h – коэффициенты трения и надежности, принимаемые по табл. 36 СНиП ∥-23-81* «Стальные конструкции».

Количество высокопрочных болтов в соединении при действии продольной силы следует определять по формуле

Где к - количество поверхностей трения соединяемых элементов.

Принимаем 10 болтов d=24 мм, устанавливаемых в отверстия d=26 мм. Указанное количество болтов устанавливается по каждую сторону от центра стыка. Проверим ослабление пояса по крайнему ряду болтов. Пояс ослаблен двумя отверстиями диаметром 26 мм по краю стыка. Площадь сечения нетто:

Ослабление пояса можно не учитывать.

В ослабленных отверстиями сечениях пояса для крайнего ряда болтов должно выполняться условие

Где А_f – площадь пояса; n_i – число рабочих болтоконтактов в проверяемом сечении; n – число рабочих болтоконтактов в соединении, здесь число рабочих болтоконтактов равно числу болтов, умноженному на число поверхностей трения.

Условие выполнено.