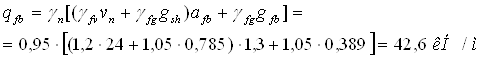Вариантное проектирование балочной клетки рабочей площадки

Содержание

1. Выбор схемы балочной клетки

1.1 Расчетные характеристики материала и коэффициенты

1.2 Выбор вариантов компоновочных схем

1.3 Определение удельных показателей

1.3.1 Проверка прочности настила

1.3.2 Проверка жесткости настила

1.4 Расчет крепления настила к балкам

1.5 Расчет прокатной балки

1.5.1 Расчетные характеристики материала и коэффициенты

1.5.2 Геометрические характеристики двутавра №30Б1

1.5.3 Статический расчет

1.5.4 Проверка прочности

1.5.5 Проверка жесткости

2. Статический расчет и подбор сечения составной сварной балки

2.1 Расчетные характеристики материала и коэффициенты

2.2 Статический расчет

2.3 Компоновка и предварительный подбор сечения составной балки

2.4 Проверка принятого сечения на прочность

3. Изменение сечения сварной балки по длине

3.1 Компоновка сечения

3.2 Определяем место изменения сечения

3.3 Проверка прочности измененного сечения

4. Проверка жесткости балки

5. Проверка общей устойчивости балки

6. Расстановка ребер жесткости и проверка местной устойчивости элементов балки

6.1 Проверка устойчивости сжатого пояса

6.2 Проверка устойчивости стенки

7. Расчет поясных швов составной балки

8. Расчет опорной части балки

8.1 Расчетные характеристики материала и коэффициенты

8.2 Определяем размеры опорного ребра

8.3 Проверка принятого сечения

8.4 Рассчитываем сварные швы, необходимые для крепления ребра к стенке

9. Расчет укрупнительного стыка балки

9.1. Расчетные характеристики материала и коэффициенты

9.2 Конструктивное решение

9.3 Расчетная длина косого шва

9.4 Расчет стыка стенки

10. Подбор сечения колонны

10.1 Расчетные характеристики материала и коэффициенты

10.2 Определение расчетной длины колонны

10.3 Определение продольной силы

10.4 Подбор сечения стержня колонны

10.5 Расчет планок

11. Расчет оголовка центрально-сжатой колонны

11.1 Определение толщины траверсы оголовка

11.2 Определение высоты траверсы

11.3 Проверка прочности траверсы

12. Расчет центрально-сжатых колонн

12.1 Определение требуемой площади опорной плиты

12.2 Определение размеров опорной плиты в плане

12.3 Определение толщины опорной плиты

12.4 Определение размеров траверс

12.5 Проверка прочности траверс

12.6 Определение требуемой высоты катета угловых швов

12.7 Назначение анкерных болтов

12.8 Определение площади верхнего обреза фундамента

1. ВЫБОР СХЕМЫ БАЛОЧНОЙ КЛЕТКИ

Задание:

Требуется выполнить компоновку балочной клетки рабочей площадки располагаемой в отапливаемом здании II уровня ответственности при следующих данных:

- шаг колонн в продольном направлении – 15,0 м;

- шаг колонн в поперечном направлении – 5,5 м;

- габариты рабочей площадки в плане – 45´11 м ;

- временная нормативная равномерно-распределенная нагрузка – 24 кН/м²;

- материал настила, балок настила, вспомогательных и главных балок, а так же колонн – сталь обычной прочности.

При заданных пролете и шаге главных балок находим оптимальную схему расположения балок настила и вспомогательных балок. Решение этой задачи производим методом вариантного проектирования.

1.1 Расчетные характеристики материала и коэффициенты

Настил относится к 3-й группе конструкций (табл. 50* (1)), поэтому сталь обычной прочности может быть С235 по ГОСТ 27772-88. Для этой стали расчетное сопротивление растяжению, сжатию, изгибу равно R_y =230 МПа при толщине листов от 2 до 20 мм, временное сопротивление стали разрыву R_un =360 МПа (табл. 51* (1)).

Балки настила и вспомогательные балки прокатного профиля относятся ко 2-й группе конструкций, принимаем сталь С245 по ГОСТ 27772-88. Для этой стали R_y =240 МПа при толщинах листов от 2 до 20 мм, R_un =370 МПа (табл. 51* (1)).

Модуль упругости стали Е = 2,06×10⁵ МПа. Коэффициент поперечной деформации (Пуассона) n=0,3 (табл. 63 (1)).

Для сооружений II уровня ответственности коэффициент надежности по ответственности g_n = 0,95 (прил. 7* ( 2 )).

Коэффициент условий работы настила и прокатных балок g_с = 1,0 (табл. 6* (1)). Коэффициенты надежности по нагрузке для постоянной нагрузки g_fg = 1,05 (табл. 1 (2)), для временной нагрузки g_fv = 1,20 (п.3.7 (2)).

Предельные относительные прогибы для настила и балок принимаются в зависимости от величины пролета по табл.19 (2). При l £ 1 м – f_u = l/120, при l = 3 м – f_u = l/150, при l = 6 м – f_u = l/200

1.2 Выбор вариантов компоновочных схем

Для сравнения принимаем два варианта компоновочных схем: балочную клетку нормального типа и усложненного.

Вариант 1. Принимаем нормальный тип балочной клетки. Определяем возможное отношение пролета настила к его толщине, предварительно вычислив:

и задавшись n₀ =l_sh / f_sh = 130, при величине временной нагрузки для расчета настила по второму предельному состоянию

n_n = g_nv₀ = 0,95×0,0024 = 0,00228 кН/см² ,

Для величины временной нагрузки v₀ = 24 кН/м рекомендуемая толщина настила 10-12мм. Принимая толщину настила 10 мм, получим предельный пролет настила

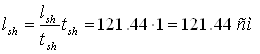
Поскольку пролет настила равен расстоянию между краями полок балок настила, то предельный шаг балок, при предварительно принятой ширине полки b_f,fb = 13 см, равен

a_fb,u = l_sh + b_f,fb = 121,44 + 13 = 134,44 см

Принимаем шаг балок настила из условия кратности пролету главной балки и возможности выполнения монтажного стыка главной балки в середине пролета. Принимаем число шагов 13, при этом 10 шагов по 130 см и 2 по 100 см. Расчетный шаг балок настила a_fb = 130 см < 134,44 см

Подбор сечения балки настила.

Погонная (линейная) нагрузка для расчета на прочность определяется по формуле

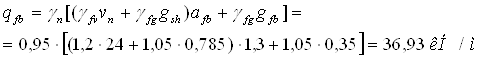
где g_fb – вес 1 м.п. балки настила, принимаем g_fb= 0,35 кН/м.

Линейная нагрузка для расчета на жесткость равна:

Балка настила является однопролетной, статически определимой с равномерно распределенной нагрузкой. Максимальный расчетный изгибающий момент в середине пролета балки определяется по формуле

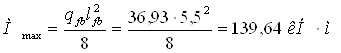
Требуемый момент сопротивления

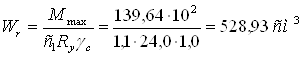
где с₁ – коэффициент, учитывающий развитие пластических деформаций, предварительно принимаем с₁ = 1,1.

Требуемый момент инерции сечения балок из условия обеспечения жесткости находим по формуле

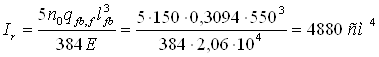
По сортаменту (ГОСТ 26020-83) подбираем двутавр с параллельными гранями полок №35Б1, для которого I = 10060 см⁴, W = 581,7 см³, g = 38,9 кг/м

Вариант 2. Балочная клетка усложненного типа. Как и в первом варианте, толщину настила принимаем 10 мм, при котором максимальный шаг балок 134,44 см. При расстоянии между главными балками 5,5 м количество шагов балок настила равно = 550/134,44 =4,1, округлив до 5, получим шаг балок настила

а_fb = 550/5 = 110 см.

Шаг вспомогательных балок при их пролете l’_fb = 5 м определяем по формуле (9)

Принимаем конструктивно удобный шаг вспомогательных балок а’_fb = l_fb= 3 м (схема балочной клетки приведена на рис.1.1)

В данном случае балки настила имеют пролет 3 м и шаг 1,375 м. Тогда погонная (линейная) нагрузка для расчета на прочность определяется по формуле

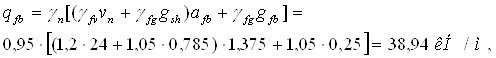
где g_fb – вес 1 м.п. балки настила, принимаем g_fb=0,25 кН/м.

линейная нагрузка для расчета на жесткость равна:

Балка настила является однопролетной, статически определимой с равномерно распределенной нагрузкой. Максимальный расчетный изгибающий момент в середине пролета балки определяется по формуле

Требуемый момент сопротивления

Требуемый момент инерции сечения балок из условия обеспечения жесткости находим по формуле:

По сортаменту (ГОСТ 26020-83) подбираем двутавр с параллельными гранями полок №20Б1, для которого I = 1943см⁴, W = 194,3 см³, g = 22,4 кг/м

Аналогично подбираем сечение вспомогательной балки, пролет которой l’_fb= 5,5 м и шаг а’_fb = 3 м. Балка загружена сосредоточенными силами (реакциями балок настила), которых 4. На стадии вариантного проектирования можно считать, что вспомогательные балки загружены равномерно распределенной нагрузкой

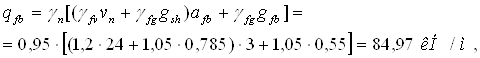
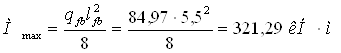
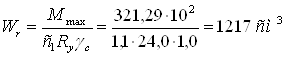
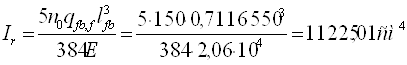
По сортаменту (ГОСТ 26020-83) подбираем двутавр с параллельными гранями полок №45Б2, для которого I = 28870 см⁴,

W = 1291,9 см³, g = 67,5 кг/м

1.3 Определение удельных показателей

Варианты компоновочных схем несущих элементов балочной площадки приведены на рис. 1.1.

а) – вариант 1: балочная клетка нормального типа;

б) – вариант 2: балочная клетка усложненного типа.

Расход стали на балки, приведенный к 1 м² площади рабочей площадки, найдем по формуле

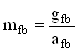
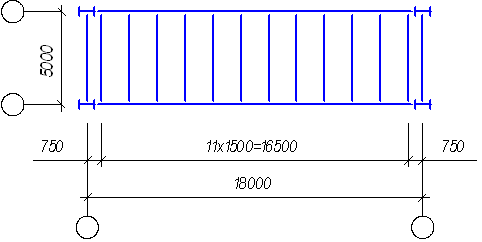
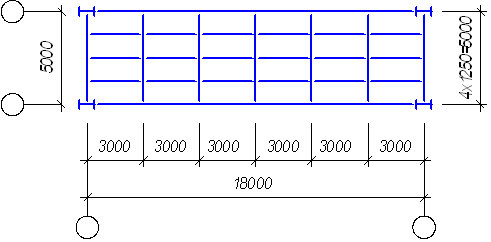
Рис.1.1. Варианты балочной клетки

Расход стали по 1 варианту (m_sh – вес настила)

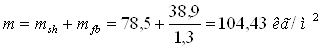
Расход стали по 2 варианту

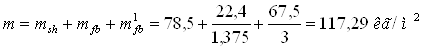
Из сопоставления показателей следует, что по расходу материала наилучшим является первый вариант, который и принимаем как основной.

1.3.1 Проверка прочности настила

Поскольку отношение большей стороны листа настила к меньшей равно 5,5/1,3 = 4,2 что больше 2, то в этом случае настил рассчитывается как длинная пластина, работающая в условиях цилиндрического изгиба только вдоль короткой стороны.

Полное напряжение в пластине равно

s_х = s_ох + s_их,

где s_ох – осевые напряжения вдоль оси х; s_ux - изгибные напряжения вдоль оси х.

Условие прочности по упругой стадии работы стали запишем по (5) в виде

,

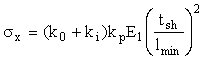где k_p – коэффициент пластины,

;

k₀ и k_i - коэффициенты, определяемые в зависимости от k_p по табл. 8.3

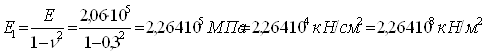
q_n - нормативная равномерно распределенная нагрузка

g_f - коэффициент надежности по нагрузке;

l_min – наименьшая сторона пластины;

t_sh – толщина настила.

Определяем коэффициент k_{p ,} при величине нагрузки

q_n= g_n(g_sh +v_n) = 0,95 (0,785 + 24) = 23,54 кН/м² = 0,002354 кН/см²

Этому значению k_pсоответствуют в табл. 8.3 (5) величины коэффициентов k₀ = 0,036 и k_i= 0,43

Тогда

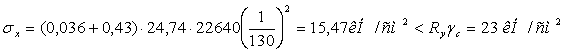
Условие прочности выполняется.

1.3.2 Проверка жесткости настила

Максимальный прогиб в середине пластины определяем по (5) в виде

f_max = k_d t_sh,

где k_d – коэффициент, принимаемый по табл.8.3 (5) в зависимости от величины k_pПри k_p=24,74 k_d = 0,605 и f_max = 0,605*1 = 0,605 см

Предельный прогиб настила по ( 2 ) равен f_u= l_sh/130 = 130/130 = 1см

Требование второго предельного состояния для настила выполняется

f_max = 0,605 см < f_u= 1см

1.4 Расчет крепления настила к балкам

Для крепления настила к балкам принимаем полуавтоматическую сварку. Для стали С235 рекомендуется сварочная проволока Св-08А и Св-08ГА (табл. 55* (1)). Принимаем Св-08А, для которой расчетное сопротивление металла швов (по табл.56 (1)) равно R_wf = 180 МПа = 18 кН/см², расчетное сопротивление металла границы сплавления для стали С235 при R_un = 360 МПа равно

R_wz= 0,45R_un= 0,45×360 = 162 МПа

Для полуавтоматической сварки b_f=0,7; b_z = 1,0 (табл. 34* (1)).

Проверяем, выполняется ли условие п. 11.2* (1) правильности выбора сварочного материала R_wz< R_wf£R_wzb_z/b_f

162 < 180< 162*1,0/0,7 = 231

Материал принят правильно, расчет можно выполнять только по металлу шва.

Цепное усилие в настиле определяем по приближенной формуле

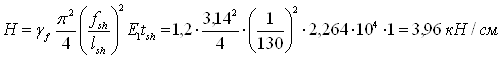
Расчетная высота углового шва, прикрепляющего настил к балке, по металлу сварного шва равна

,

где l_w – расчетная длина углового шва, l_w = 1,0 см

Минимальный катет шва, в соответствии с табл. 38* (1), при толщине свариваемых элементов – 10 мм (настил) и 8,5 мм (полка двутавра 30Б1) будет 4мм. Принимаем сварной шов для крепления настила к балкам высотой по катету k_f = 4мм.

1.5 Расчет прокатной балки

Выполнить проверку балки настила варианта балочной клетки, принятого в качестве основного в примере 1.

Исходные данные (по результатам компоновки основного варианта)

- настил – лист толщиной 10 мм;

- балка настила – двутавр №35Б1 по ГОСТ 26020-83;

- пролет балок настила l_fb= 5,5 м;

- шаг балок настила а_fb = 130 см;

- материал балок сталь обычной прочности.

1.5.1 Расчетные характеристики материала и коэффициенты

Балки настила прокатного профиля относятся ко второй группе конструкций, принимаем сталь С245 по ГОСТ 27772-88. для этой стали Ry=240 Mпа при толщине проката от 2 до 20 мм. R_un=370Mпа. Модуль упругости=2,06*10⁵Мпа. Для сооружений II уровня ответственности коэффициент надежности по ответственности g_n = 0,95 (прил. 7* (2)).

Коэффициент условий работы настила и прокатных балок g_с = 1,0 (табл. 6* (1)).

Коэффициенты надежности по нагрузке для постоянной нагрузки g_fg = 1,05 (табл. 1 (2)), для временной нагрузки g_fv = 1,20 (п.3.7 (2)).

Предельные относительные прогибы для балок принимаются в зависимости от величины пролета по табл.19 (2). При l = 6 м – f_u = l/200=3 см.

1.5.2 Геометрические характеристики двутавра №35Б1

Геометрические характеристики принимаем по сортаменту горячекатаных двутавров по ГОСТ 26020-83:

- высота сечения h = 346 мм,

- толщина стенки t_w = 6,2 мм,

- ширина полки b_f= 155 мм,

- толщина полки t_f= 8,5 мм,

- площадь сечения А = 49,53 см²,

- момент инерцииI = 10060 см⁴,

- момент сопротивления W = 581,7 см³.

Масса профиля g = 38,9 кг/м

Площадь полки A_f = t_fb_f = 0,85×15,5 = 13,175 см².

Площадь стенки A_w = A – 2A_f = 49,53 - 2×13,175 = 23,28см²

1.5.3 Статический расчет

Уточняем нагрузку на балку

Погонная (линейная) нагрузка для расчета на прочность

где g_fb – вес 1 м.п. балки настила, g_fb=0,389 кН/м.

Линейная нагрузка для расчета на жесткость равна:

Определяем расчетные усилия

Максимальный расчетный изгибающий момент в середине пролета балки

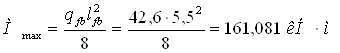
Максимальная поперечная сила на опоре

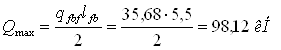
1.5.4 Проверка прочности

Касательные напряжения в опорном сечении балки проверяем по формуле

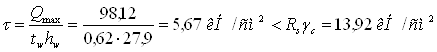
где R_s = 0,58R_y = 0,58×240 = 139,2 МПа

Поскольку t = 56,7 МПа < 0,5Rs = 0,5×139,2 = 69,6 МПа, то с₁ = с в формуле проверки нормальных напряжений. Коэффициент с принимаем по табл. 66 (1), а зависимости от отношения A_f/A_w = 13,175/23,18 = 0,56, при котором с = 1,11. Выполняем проверку нормальных напряжений

Требование прочности выполняется

1.5.5 Проверка жесткости

Определяем прогиб балки в середине пролета

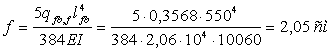
Требование второго предельного состояния выполняется, так как

f=2,05 см < f_u= 2,5 см

2. СТАТИЧЕСКИЙ РАСЧЕТ И ПОДБОР СЕЧЕНИЯ СОСТАВНОЙ СВАРНОЙ БАЛКИ

Подобрать сечение составной сварной балки, являющейся главной балкой рабочей площадки, компоновка которой выполнена в предыдущем пункте.

Исходные данные:

(а) по заданию на проектирование

- пролет главной балки l_mb = 15,0 м;

- шаг главных балок a_mb = 5,5 м;

- строительная высота перекрытия неограниченна;

- материал – углеродистая сталь обычной прочности;

- временная равномерно распределенная нагрузка на площадку v_n = 24 кН/м² (вся временная нагрузка длительная).

(б) по результатам выполнения предшествующих разделов

- количество балок настила, опирающихся на главную балку 12 (10 шагов по 1,3 м и 2 шага по 1 м);

- шаг балок настила a_fb= 1,3 м;

- балки настила - двутавры 35Б1 (по ГОСТ 26020-83), ширина полки b_f,fb= 155 мм;

- реакция балки настила Q_fb = 98,12 кН;

- постоянные нагрузки: от массы настила g_sh,n= 0,785 кН/м², от балок настила g_fb,n= 0,35кН/м².

2.1  Расчетные характеристики материала и коэффициенты

Сварные балки перекрытия относятся к 1-й группе конструкций (табл. 50* (1)). Сталь обычной прочности, соответствующую этой группе, принимаем С255 по ГОСТ 27772-88. Расчетное сопротивление стали принимаем для листов толщиной до20 мм (предполагаемая толщина поясов балки) R_y= 240МПа, R_un = 370 МПа (табл. 51* (1)), E = 2,06×10⁵ МПа, n = 0,3 (табл. 63 (1)). Для сооружений II уровня ответственности (прил.7* (2)) коэффициент надежности по ответственности равен g_n= 0,95.

Коэффициент условий работы при расчете на прочность g_c=1,0, при расчете на устойчивость g_c=0,95 (табл. 6 (1)).

Коэффициенты надежности по нагрузке g_fg =1,05 (п.2.2 (2)), g_fv=1,20 (п.3.7 (2)).

Предельный относительный прогиб главной балки f_mb,u = l_mb/250, (п.2, табл. 19 (2)).

2.2  Статический расчет

Расчетную схему главной балки принимаем в виде разрезной шарнирно-опертой однопролетной балки. Поскольку число сосредоточенных грузов от давления балок настила более 5, то нагрузку принимаем в виде равномерно распределенной.

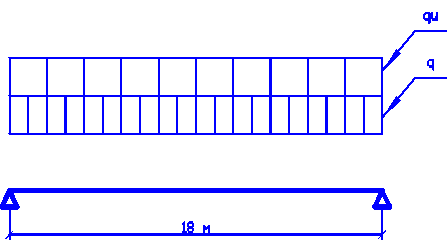
Рис. 2.1. Расчетная схема балки

Погонная (линейная) нагрузка для расчета на прочность определяется по формуле

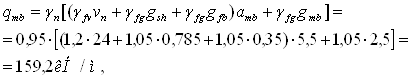
где g_mb – вес 1 м.п. главной балки, принимаем g_mb=2,5 кН/м.

Линейная нагрузка для расчета на жесткость равна:

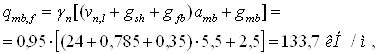
Максимальный расчетный изгибающий момент в середине пролета балки

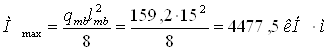
Максимальная поперечная сила на опоре

.

Изгибающий момент в середине пролета балки от нагрузки для расчета на жесткость

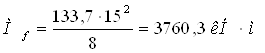
2.3  Компоновка и предварительный подбор сечения составной балки

Принимаем гибкость стенки l_w=125, в соответствии с рекомендациями (3). Минимальная толщина стенки равна t_w,min= 12 мм.

Определяем минимальную высоту сечения сварной балки при предельном относительном прогибе (f_mb /l_mbu =1/250)

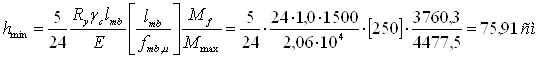
Находим минимальную толщину стенки из условия предельного прогиба

.

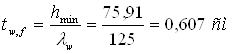Толщина стенки из условия прочности на срез равна

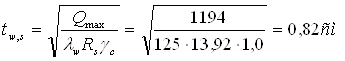
где R_s=0,58R_y=0,58×240=139,2 МПа.

Определяем наименьшую толщину стенки из условия смятия, поскольку принимаем этажное сопряжение балок в балочной клетке. В каждом узле опираются две балки настила, поэтому F=2Q_fb = 2 ×98,12=196,24 кН. Толщиной полки главной балки задаемся t_f=2 см.

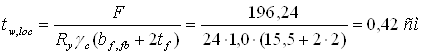
Находим толщину стенки, соответствующую балке оптимальной высоты.

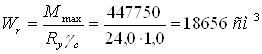
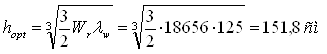
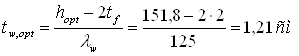
Сравниваем все полученные значения толщины стенки: t_w,min= 1,2см; t_w,f= 0,6см; t_w,s= 0,82см; t_w,loc= 0,42см; t_w,opt= 1,21см.

Наибольшее значение из этого ряда t_w.opt= 1,21 см показывает, что следует принимать высоту балки, соответствующую t_w,opt.

Принимаем толщину стенки 13 мм, тогда высота стенки будет равна

h_w = t_wl_w=1,3×125 = 156 см.

Принимаем размеры стенки с учетом стандартных размеров ГОСТ 19903-74^*

h_wх t_w = 1700 х 13 мм.

Определяем размеры поясных листов. Требуемая площадь поясов (принимая h=h_w) равна

Требования, предъявляемые к размерам поясных листов и диапазон определяемых величин следующие:

b_f=(1/3…1/5)h = 57…34см;

b_f,min= 18,0см;

t_f,max= 3 t_w= 3×1,3=3,9 см;

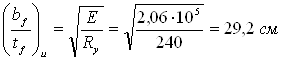
Принимаем размеры поясных листов с учетом ослабления верхнего пояса отверстиями для болтов крепления балок настила b_fx t_f = 500 x 20 мм, которые удовлетворяют всем вышеуказанным требованиям. Подобранное сечение показано на рис. 2.2.

2.4  Проверка принятого сечения на прочность

Определяем геометрические характеристики принятого сечения балки.

Для крепления балок настила к главным принимаем болты диаметром 16 мм (каждая балка крепится двумя болтами). Верхний пояс оказывается ослабленным отверстиями диаметром 19 мм (d₀ = 1,9см), в каждом сечении два отверстия. Расстояние от центра тяжести сечения до оси, проходящей через середину высоты балки

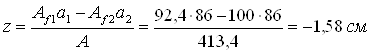
где A_f1=b_f1t_f1 - d₀t_f1= 50×2 – 2×1,9×2,0 = 92,4 см²- площадь сечения верхнего пояса;

A_f2=b_f1 t_f1 = 50×2,0 = 100 см² - площадь сечения нижнего пояса;

 A= A_f1+A_f2+A_w= 92,4 + 100 +170×1,3=413,4 см²- площадь сечения балки;

а₁ = a₂ = 170/2 + 2/2 = 86 см.

Момент инерции равен.

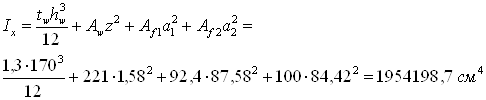
где a₁= 86 + 1,58 = 87,58 см – расстояние от центра тяжести сечения до центра тяжести верхнего пояса; a₂= 86 – 1,58 = 84,42 см – расстояние от центра тяжести сечения до центра тяжести нижнего пояса;

Минимальный момент сопротивления нетто (с учетом ослабления сечения)

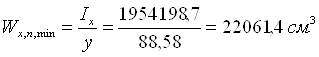
где y = 87,58 + 1,0 = 88,58 см – расстояние от центра тяжести сечения до наиболее удаленного волокна.

Статический момент полусечения

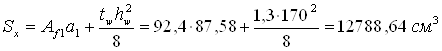
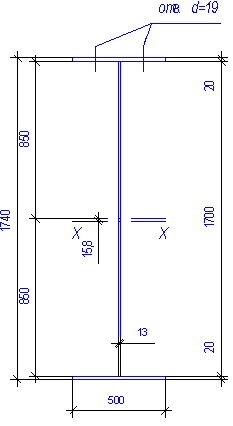
Рис.2.2. Сечение сварной балки

Проверка прочности:

а). по нормальным напряжениям от изгиба

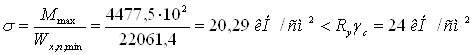
Недонапряжение составляет Ds = (240-203) ×100/240 = 15,4% > 5%

б). по касательным напряжениям

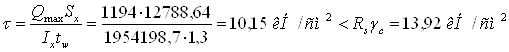
в). по напряжениям смятия в стенке

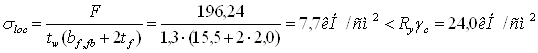
Прочность балки обеспечена

проект балка клетка рабочая площадка

3. ИЗМЕНЕНИЕ СЕЧЕНИЯ СВАРНОЙ БАЛКИ ПО ДЛИНЕ

Изменить сечение по длине балки, рассчитанной в пункте 1

Исходные данные (принимаются по результатам выполнения примера 1):

- l_{m b} = 15,0 м;

- q_mb,= 159,2 кН/м;

- сечение главной балки:b_f =50 см, t_f = 2,0 см, h_w=170 см, t_w = 1,3 см;

- шаг балок настила a_fb = 130 см (крайние шаги по 0,75 м);

- поперечная сила на опоре Q_max= 1194 кН;

Изменение сечения главной балки осуществляем за счет изменения ширины поясных листов. Стыки листов выполняем прямым швом с визуальным контролем качества.

3.1 Компоновка сечения

Находим требуемую минимальную ширину пояса

_1f= b_f/2 = 500/2 = 250 мм, _1f= 180 мм, _1f= h/10 = 170 мм.

Учитывая, что верхний пояс ослаблен отверстиями, ширину сечения принимаем больше, чем требуется. Принимаем сечение пояса _1fxt_f= 300 x 20 мм. Сечение стенки не изменяется h_w=170 см, t_w = 1,3 см.

3.2 Определяем место изменения сечения

Определяем геометрические характеристики измененного сечения с учетом возможного ослабления верхнего пояса двумя отверстиями d₀ = 19 мм.

Расстояние от центра тяжести сечения до оси, проходящей через середину высоты балки, равно

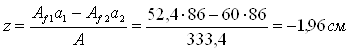
где A_f1=b_f1 t_f1 – d₀ t_f1= 30×2,0 – 2×1,9×2,0 = 52,4 см²- площадь сечения верхнего пояса;

A_f2=b_f1 t_f1 = 30×2,0 = 60,0 см²- площадь сечения нижнего пояса;

A= A_f1+A_f2+A_w= 52,4 + 60,0 + 170×1,3 = 171,4 см²- площадь сечения балки.

Момент инерции измененного сечения балки равен

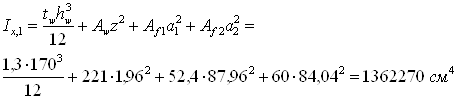
где a₁= 86 + 1,96 = 87,96 см – расстояние от центра тяжести сечения до центра тяжести верхнего пояса;

a₂= 86 – 1,96 = 84,04 см – расстояние от центра тяжести сечения до центра тяжести нижнего пояса; Минимальный момент сопротивления нетто (с учетом ослабления сечения)

где y= 87,96 + 1 = 88,96 см – расстояние от центра тяжести сечения до наиболее удаленного волокна.

Статический момент полусечения

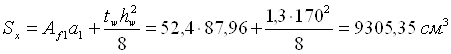
Предельный изгибающий момент, воспринимаемый измененным сечением, определяем по формуле

M_1r = W_1xR_wyg_c = 15313,29*20,40*1,0 = 312391,12 кН×см = 3123,91 кН×м

где R_wy =0,85 R_y= 0,85 ×240 = 204 МПа

Находим место изменения сечения при равномерно распределенной нагрузке по формуле

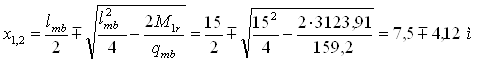
x₁=3,38 м, x₂ = 11,7 м.

Принимаем место изменения сечения на расстоянии от опор 3,30м (рис. 2.1)

3.3  Проверка прочности измененного сечения

а). по нормальным напряжениям:

изгибающий момент в месте измененного сечения (х = 3,00 м)

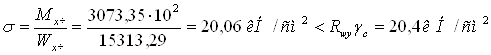
б) по касательным напряжениям:

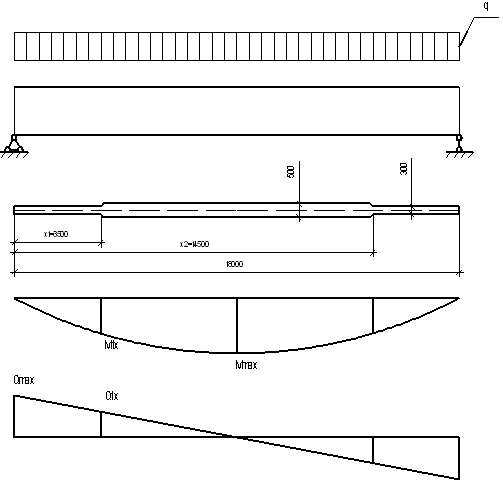
Рис.2.1. Изменение сечения сварной балки по длине

- в месте изменения сечения

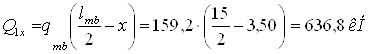
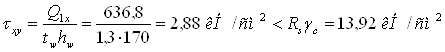
- на опоре

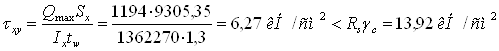
в) по приведенным напряжениям:

балки настила опираются на расстоянии 0,1 м, 2,3 м и 3,6 м от опор, а расстояние до места изменения сечений 3,3 м, то есть в месте изменения сечения s_loc = 0.

На уровне поясных швов нормальные напряжения равны

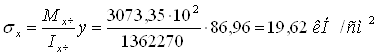
y =a₁ – t_f /2 = 87,96 – 2,0/2 = 86,96 см

Приведенные напряжения

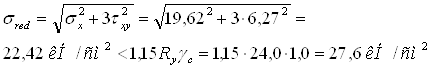
Проверки показали, что прочность измененного сечения обеспечена.

4. ПРОВЕРКА ЖЕСТКОСТИ БАЛКИ

Выполнить проверку жесткости балки, подобранной в примерах 1 и 2.

Исходные данные:

- l_mb = 15,0 м;

- q_mb,f= 133,7 кН/м;

- I_x= 1954198,7 см⁴;

- I_x,1 = 1362270 см⁴.

Находим прогиб главной балки переменного сечения, предварительно определив:

- прогиб главной балки постоянного сечения

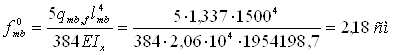
- коэффициент a

-

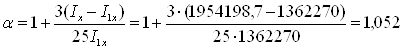
f_mb=f⁰_mba = 2,18×1,052 = 2,29 см.

Предельный прогиб

f_mb,u= l_mb/ 250 = 1500/250 = 6 см.

Сравниваем фактический прогиб с предельным f_mb = 2,29 см.< f_mb,u = 6 см.

Подобранное сечение балки удовлетворяет требованиям второй группы предельных состояний – жесткости.

5. ПРОВЕРКА ОБЩЕЙ УСТОЙЧИВОСТИ БАЛКИ

Проверить общую устойчивость балки, подобранную в примерах 1 и 2.

Исходные данные:

- размеры поясов балки b_f= 500 мм, t_f= 20 мм;

- расстояние между осями поясных листов – h = 1720мм.

Нагрузка на главную балку передается через балки настила, установленные с шагом a_fb=1,5 м и закрепляющие главную балку в горизонтальном направлении. Проверяем условие п. 5.16,б (1) в середине пролета

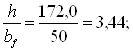
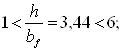
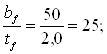
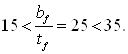
По табл. 8* (1) находим наибольшее значение (l_ef/b_f)_u, при котором не требуется расчета на устойчивость, принимая l_ef= a_fb = 1,5 м

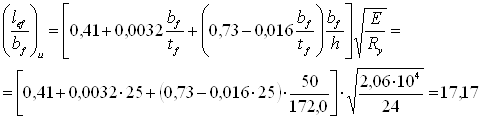
Поскольку

(l_ef/b_f)= 150/50 = 3 < (l_ef/b_f)_u = 17,17

то устойчивость балки обеспечена и расчет на общую устойчивость выполнять не требуется.

6. РАСТАНОВКА РЕБЕР ЖЕСТКОСТИ И ПРОВЕРКА МЕСТНОЙ УСТОЙЧИВОСТИ ЭЛЕМЕНТОВ БАЛКИ.

Проверить устойчивость элементов балки, подобранной в примерах 1 и 2. Исходные данные:

- сечение балки - b_f =50 см, t_f = 2,0 см, h_w=170 см, t_w = 1,3 см;

- шаг балок настила a_fb = 130 см.

6.1 Проверка устойчивости сжатого пояса.

Отношение ширины свеса пояса к толщине при b_ef= (b_f-t_w)/2 = (50-1,3)/2=24,35 см равно b_ef/t_f = 24,35/2,0=12,18 Предельное отношение ширины пояса к толщине по табл.30 (1) равно

При b_ef/t_f = 12,18 < (b_ef/t_f)_u = 14,65 устойчивость пояса обеспечена.

6.2 Проверка устойчивости стенки

Проверяем необходимость постановки ребер жесткости. Условная гибкость стенки при h_ef=h_w= 170 см и t_w =1,3 см равна

Поскольку , то постановка ребер жесткости необходима (п.7.10 (1)). Максимальное расстояние между поперечными ребрами жесткости при  равно a_max = 2h_ef=2×170 = 340 см.

Расстояние между поперечными ребрами жесткости принимаем 300 см (2,3 шага балок настила).

Расстановка поперечных ребер жесткости показана на рис. 6.1. с учетом выполнения монтажного стыка в середине пролета.

Принимаем парные ребра жесткости, ширина которых по (2) равна:

Толщина ребра определяется по п. 7.10 (1)

Принимаем размеры двухсторонних ребер жесткости b_hxt_s =100x7 мм

Проверяем необходимость выполнения проверки стенки на устойчивость по п. 7.3 (1), учитывая, что в каждом отсеке имеется местная нагрузка от давления балок настила (s_loc ¹ 0):  В этом случае проверка стенки балки на устойчивость необходима.

Проверяем отсек стенки балки, в котором изменяется сечение ее пояса. Ширина отсека а = 300 см, расчетная высота стенки 170 см.

Так как длина отсека превосходит его расчетную высоту, то при вычислении средних значений M и Q в отсеке принимаем расчетный участок, равный по длине расчетной высоты отсека.

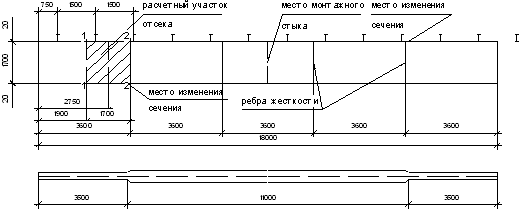
Рис. 6.1. К расчету устойчивости стенки составной балки

Последовательно определяем:

- изгибающий момент в сечении на границе расчетного участка отсека в точках 1 и 2 (рис. 6.1)

х₁= 300 – 170 = 130 см,

х₂=300 см,

- среднее значение момента на расчетном участке отсека

M_x=(M₁+M₂)/2 = (2071,98+3438,72)/2 = 2755,35 кН×м;

- поперечную силу в сечениях 1 и 2

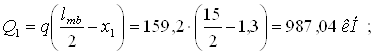
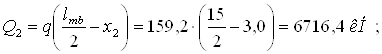
- среднюю поперечную силу в пределах расчетного участка отсека

Q_x=(Q₁+Q₂)/2 = (987,04+716,4)/2 = 851,72 кН.

Определяем компоненты напряженного состояния по п.7.2 (1) в стенке для уменьшенного сечения

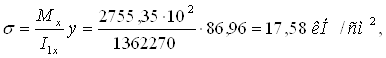
где I_1x=1362270 см⁴;

y = h/2+z = 170/2 + 1,96 = 86,96 см.

,

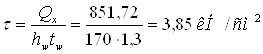_loc=7,7 кН/см² (см. пункт 2.4.)

Определяем критические значения компонентов напряженного состояния.

При отношении a/h_ef = 300/170 = 1,76> 0,8 и _loc / = 7,7/17,58=0,43 предельное отношение (_loc /)_u принимается по табл.24 (1) в зависимости от параметра d и отношения a/h_ef

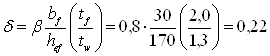, при b=0,8 по табл.22(1).

При d= 0,22 и a/h_ef = 2,12 (_loc / )_u= 0,618.

Тогда при a/h_ef = 2,12 > 0,8 и _loc / = 0,4 < (_loc /)_u= 0,618 находим _crпо формуле (75) (1) и _loc,cr– формуле (80) (1), но с подстановкой 0,5а вместо а при вычислении  в формуле 80 и в табл. 23 (1)

,

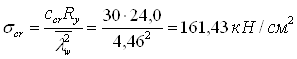С_cr= 30 по табл. 21 (1)

Для определения _loc,cr предварительно находим c₁ по табл.23 (1) при 0,5a/h_ef = 150/170 =0,88 и d = 0,22 c₁ = 18,25

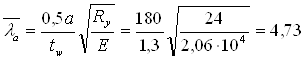
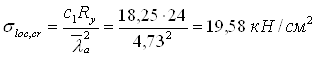
Определяем t_cr по формуле (76) (1) при m = 360/170 = 2,12

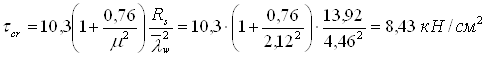
Проверку устойчивости стенки выполняем по формуле (79) (1)

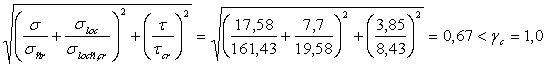
Принятая расстановка ребер жесткости обеспечивает устойчивость стенки.

7. РАСЧЕТ ПОЯСНЫХ ШВОВ СОСТАВНОЙ БАЛКИ

Рассчитать поясные швы в составной сварной балке.

Исходные данные:

- сечение балки на опоре h_w x t_w =1700x1,3 мм, b_f x t_f = 500x20 мм;

- поперечная сила на опоре Q_max= 1194 кН;

- опорная реакция балки настила Q_fb = 98,12 кН.

Для поясного соединения принимаем двусторонние угловые швы, поскольку не выполняются требования, предъявляемые к балке для случая применения односторонних швов, в частности, сжатый пояс не раскреплен сплошным настилом и не во всех местах приложения к поясу сосредоточенных нагрузок (опирание балок настила) установлены ребра жесткости (см. п. 13.26 (1)) Расчет выполняем для наиболее нагруженного участка шва у опоры под балкой настила.

Определяем геометрические сечения брутто относительно нейтральной оси

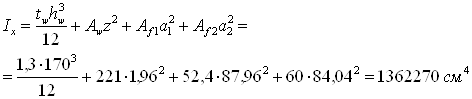
где a₁= 86 + 1,96 = 87,96 см – расстояние от центра тяжести сечения до центра тяжести верхнего пояса;

a₂= 86 – 1,96 = 84,04 см – расстояние от центра тяжести сечения до центра тяжести нижнего пояса;

Статическиймомент полусечения

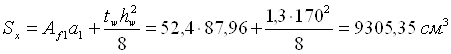
Определяем расчетные усилия на единицу длины шва:

- погонное сдвигающее усилие

- давление от сосредоточенного груза F = 2Q_fb= 2×98,12 = 196,24 кН

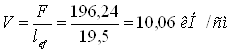
где l_ef- условная длина распределения сосредоточенно