Анализ факторов, определяющих равновесие потребителя и его реакцию на изменение цены и дохода

Посетив любой рынок, мы чувствуем, что суть рыночного процесса – купля-продажа товара. Главными действующими лицами здесь являются продавцы и покупатели. Поэтому понять закономерности работы рынка можно, только разобравшись в том, чем руководствуются на рынке покупатели и к чему стремится продавец.

Вопрос устройства рынка волновал ученых с давних времен. Еще в 1776 году, когда была подписана Декларация о независимости, в Англии была опубликована одна из самых важных книг нашего времени – «Исследование о природе и причинах богатства народов». Она принесла своему автору Адаму Смиту титул «отца экономики».

Смит отошел от принципиальных взглядов своего времени. С точки зрения Смита, богатство нации создается в процессе производства, и не только сельскохозяйственного.

Центральная идея учения Смита заключалось в том, что экономика будет функционировать лучше, если исключить ее функционирование государством. В этих условиях экономический эгоизм будет заставлять предприятия выпускать продукты, нужные покупателям, и делать это по максимально низкой цене. Они будут делать это, думая не о благоденствии общества, а пытаясь превзойти своих конкурентов и получить максимум прибыли. Но этот эгоизм принесет пользу всему обществу тем, что обеспечит больше товаров и услуг лучшего качества и по более низким ценам.

Для объяснения, почему все общество выиграет, если экономика будет свободна от регулирования, Смит использовал метафору «невидимой руки».

«Каждый отдельный человек старается употребить свой капитал так, чтобы продукт его обладал наибольшей стоимостью. Обычно он не имеет ввиду содействовать общественной пользе, а преследует лишь собственный интерес. Однако при этом, как и во многих других случаях, он невидимой рукой направляем к цели, которая совсем не входила в его намерения.

Преследуя свои собственные интересы, он неизбежно предпочитает такие действия, которые наилучшим образом служат интересам общества». «Невидимой рукой» Адам Смит именовал те экономические силы, которые мы сегодня называем спросом и предложением.

Раздел 1

1.1 Множество допустимых возможностей потребителя. Бюджетная линия

Рассмотрим множество возможностей потребителя, т.е. множество всех доступных потребителю товарных наборов.

Представим, прежде всего, что потребитель располагает в данный период денежной суммой, например, в 1000 руб. Понятно, что истратить эту сумму в принципе можно весьма различными способами: можно купить на все деньги жевательной резинки, можно - учебников по экономике, одну пачку резинки, а на остальные деньги еще чего-нибудь, что душа пожелает. Иными словами, наш потребитель может купить любой набор товаров, удовлетворяющий лишь одному простому требованию: общие расходы на данный набор не превышают суммы денег, находящейся в распоряжении потребителя - 1000 руб.

Сформулируем это правило в более общем виде. Пусть потребитель располагает в единицу времени некоторым доходом М. Отметим, что экономиста в данном случае совершенно не интересует источник этого дохода (были ли деньги заработаны, взяты в долг или выручены от продажи имущества), важно лишь, что потребитель в течение данного периода не может расходовать свыше М денежных единиц. Тогда, как уже говорилось выше, потребитель может приобрести любой набор товаров Х = (x₁, x₂, ..., x_n), удовлетворяющий следующему условию

P₁ x₁ + P₂x₂ + … + P_nx_n = M                                                        (1)

где x₁, x₂, ..., x_n — количество единиц товаров 1, 2,..., n, приобретаемых потребителем; , P₂,..., P_n — цены этих товаров; М — располагаемый доход потребителя.

Выражение (1) называется бюджетным ограничением потребителя. Вспомним, что графические методы анализа заставляют нас рассматривать случай, когда потребительский выбор ограничен двумя товарами (назовем их товар Х и Y). Тогда бюджетное ограничение имеет вид

P_Xx + P_Yy = M                                                                            (2)

Для того чтобы представить множество товарных наборов, удовлетворяющих ограничению (2) в графическом пространстве товаров, нам необходимо, очевидно, отобразить в пространстве товаров границу этого множества, т.е. линию

P_Xx + P_Yy = M.                                                                           (3)

Линия, описываемая уравнением (3), носит название бюджетной линии.

Примем теперь очень важное предположение:

предположим, что отдельный потребитель не может повлиять на цену какого-либо товара, сколь значительно бы этот потребитель не изменял свой объем потребления данного товара (иными словами, на рынке существует совершенная конкуренция на стороне спроса). В самом деле, трудно себе представить, чтобы доля отдельного потребителя на рынке некоторых потребительских товаров (продуктов питания, одежды, обуви, бытовой техники и т.д.) была столь велика, чтобы изменение спроса одного лишь потребителя, например, на мясные продукты или компакт диски могло бы привести к изменению цены на эти товары. Таким образом, цены товаров выступают для потребителя как некие внешние, заданные рынком величины.

Вернемся теперь к уравнению (3) и попробуем представить бюджетную линию графически. Заметим, что уравнение (3) легко преобразуется в уравнение

y = M/P_Y – (P_X/P_Y)x.                                                                   (4)

Поскольку величины М, Р_X и Р_Y, по нашему предположению, постоянны, уравнение (4) представляет собой уравнение прямой линии (типа y = ax + b), где М/Р_Y — свободный член, а –Р_X/Р_Y — коэффициент при переменной х. Бюджетная линия соответственно представляет собой прямую линию типа линии АВ, изображенной на рис. 1.

Рис. 1. Бюджетная линия

Координаты точек А и В (точки пересечения бюджетной линии с осями координат) характеризуют максимальные количества товаров Х и Y, которые может приобрести потребитель, истратив весь свой доход только на товар Х или только на товар Y. Так, ордината точки А y_A = М/Р_Y. Именно столько товара Y может купить потребитель, вовсе отказавшись от приобретения товара X. Аналогичным образом абсцисса точки В x_B = = М/Р_X. Любой другой находящийся на бюджетной линии набор товаров С = (x_c, y_c) имеет для потребителя точно такую же стоимость М, что и наборы А = (0, М/Р_Y) и В = (М/Р_X, 0). Вообще говоря, бюджетная линия - это геометрическое место точек, характеризующих все наборы товаров, которые может приобрести потребитель, полностью израсходовав свой доход М при данных ценах товаров Р_X и Р_Y.

Как видно из рис. 1, бюджетная линия имеет отрицательный наклон. Такое свойство бюджетной линии вполне объяснимо: поскольку наборы товаров, находящиеся на бюджетной линии, имеют одинаковую стоимость, увеличение объема закупок одного товара возможно лишь за счет сокращения потребления другого товара. Вспомним, что наклон прямой линии характеризуется коэффициентом при переменной х в уравнении этой прямой. Следовательно, наклон бюджетной линии характеризуется величиной Р_X/Р_Y (см. (4)). Знак “минус” как раз и указывает на отрицательный наклон бюджетной линии (так как цены товаров — положительные величины, т. е. Р_X > 0, Р_Y > 0, то величина Р_X/Р_Y отрицательная). Наклон бюджетной линии равен, таким образом, соотношению цен товаров, взятому с противоположным знаком. Наклон этот, как видно, является постоянной величиной, поскольку мы предположили ранее, что отдельный потребитель не способен повлиять на рыночные цены товаров.

Теперь, когда мы уже знаем свойства бюджетной линии, представим графически множество всех наборов товаров, удовлетворяющих бюджетному ограничению. Поскольку объемы потребления не могут быть отрицательными величинами (x =0, y =0), доступное множество представляет собой заштрихованный на рис. 2 треугольник ОАВ, ограниченный бюджетной линией и осями координат.

Рис. 2. Множество возможностей потребителя

K и L - доступные наборы, D и Е - недоступные

Поскольку конечной целью нашего анализа является изучение реакции потребителя на изменение цен и дохода, нам необходимо, очевидно, рассмотреть, как изменяются при изменении цен и доходов границы доступного множества. Начнем с изменения дохода. Пусть первоначально доход потребителя составлял М₁. Тогда бюджетная линия описывается уравнением (линия АВ на рис. 3)

y = M₁/P_Y – (P_X/P_Y)x.                                                                   (5)

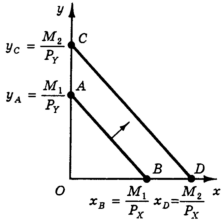
Рис. 3. Сдвиг бюджетной линии при изменении дохода

Предположим теперь, что доход потребителя увеличился с М₁ до а цены товаров остались неизменными. Тогда уравнение новой бюджетной линии имеет вид

y = M₂/P_Y – (P_X/P_Y)x.                                                                   (6)

Простое сравнение показывает, что коэффициент при переменной х в уравнении (6) остался таким же, как и в уравнении (5), а значит, не изменился наклон бюджетной линии, который определяется соотношением цен.

Зато изменились координаты точек пересечения бюджетной линии с осями координат: новая бюджетная линия пересекает ось y в точке С с ординатой y_c = М₂/P_Y, а ось x — в точке D с абсциссой x_D = М₂/P_X.

Таким образом, увеличение дохода при неизменных ценах приводит к параллельному сдвигу бюджетной линии вверх (а снижение дохода соответственно к параллельному сдвигу бюджетной линии вниз).

Вернемся теперь к первоначальной бюджетной линии АВ, описываемой уравнением (5), и рассмотрим еще одну весьма важную в экономике ситуацию: пусть теперь изменится цена лишь одного товара Х (например, уменьшится с P_X до P_X¹), в то время как цена товара Y и доход потребителя останутся неизменными. Тогда новое бюджетное ограничение примет вид

y = M₁/P_Y – (P_X¹/P_Y)x.                                                                  (7)

В этом случае коэффициент при переменной х изменится с –P_X/PY на –P_X¹/P_Y, а следовательно, изменится и наклон бюджетной линии. Неизменной останется точка пересечения бюджетной линии с осью y — точка А. Поскольку доход М₁, и цена P_Y не изменились, максимально возможный объем закупок потребителем товара Y по-прежнему составляет М₁/P_Y единиц товара Y. В то же время точка пересечения бюджетной линии с осью х сместилась вправо (рис. 4).

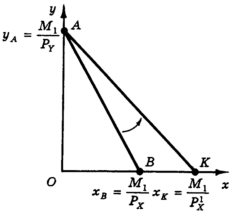
Рис. 4. Поворот бюджетной линии при изменении дохода

Если первоначальная бюджетная линия пересекает ось х в точке В с абсциссой x_B = М₁/P_Y, то “новая” бюджетная линия (при цене P_X¹ < P_X пересекает ось х в точке K с абсциссой x_k = М₁/P_X¹. Иными словами, поскольку цена товара Х уменьшилась, потребитель может теперь, израсходовав весь свой доход на товар X, купить большее количество единиц этого товара. Таким образом, уменьшение цены товара Х приводит к повороту бюджетной линии против часовой стрелки вокруг точки пересечения бюджетной линии с осью y (а увеличение цены товара Х — к аналогичному повороту по часовой стрелке).

1.2 Оптимум потребителя

Попробуем теперь с помощью уже известного нам инструментария кривых безразличия и бюджетных линий построить модель потребительского выбора с тем, чтобы определить: какими же свойствами обладает тот набор товаров, который выбирает потребитель из множества доступных ему товарных наборов при данных ценах товаров и доходе?

Итак, пусть потребитель располагает некоторым доходом, который он может тратить на приобретение двух товаров, причем цены этих товаров не зависят от объемов закупок данного потребителя. Тогда множество доступных потребителю товарных наборов может быть представлено графически с помощью бюджетной линии, свойства которой описаны в разделе 1 данного проекта. Пусть при этом система предпочтений потребителя удовлетворяет предположениям I-III ординалистской теории полезности и, следовательно, эта система предпочтений может быть представлена в графическом пространстве товаров в виде карты безразличия данного потребителя. Изобразим теперь карту безразличия и бюджетную линию на одном графике (рис. 5). Какой набор товаров выберет наш потребитель при данных бюджетном ограничении и карте безразличия?

Рис. 5. Оптимум потребителя

Прежде всего мы должны, очевидно, сформировать критерий потребительского выбора. Критерий этот, впрочем, нам уже известен из предыдущего обсуждения: потребитель, по нашему предположению, стремится максимизировать получаемую им полезность, т.е. выбирает наиболее предпочтительный для себя набор товаров из множества доступных ему наборов.

На графике (рис. 5) множество доступных нашему потребителю товарных наборов отображается треугольником ОАВ.

Представим себе вначале, что точка потребительского выбора в доступном множестве лежит ниже бюджетной линии АВ. Это означает, что некоторая часть потребительского дохода осталась неизрасходованной. В рамках нашей модели, однако, доход может тратиться лишь на приобретение двух товаров, причем возможность сбережений не предусматривается. В этих условиях дополнительные закупки товаров на неизрасходованные денежные средства, очевидно, будут увеличивать извлекаемую потребителем полезность, что следует из предположения ординалистской теории полезности — “больше — лучше, чем меньше”. Иными словами, точка потребительского выбора обязательно должна лежать на бюджетной линии АВ.

Какая же из точек на бюджетной линии соответствует оптимальному, с точки зрения потребителя, набору товаров? Рассмотрим точку F. Точка F лежит на пересечении бюджетной линии АВ и кривой безразличия I₁. Кривая безразличия I₁ пересекает бюджетную линию также в точке G. Очевидно, что точки F и G не являются наиболее предпочтительными для потребителя, поскольку при движении вниз по бюджетной линии от точки F и вверх по бюджетной линии от точки G потребитель переходит на более высоко расположенные кривые безразличия и, следовательно, на более высокий уровень полезности. Рассмотрим теперь точку С, более предпочтительную, чем точка F. Точка С лежит на кривой безразличия I₂ пересекающей бюджетную линию в точке D. Точки С и D не являются точками оптимального потребительского выбора по тем же причинам, что и точки F и G. Вообще говоря, из свойств кривых безразличия и из рис. 5 очевидно, что если некоторая кривая безразличия пересекает бюджетную линию в двух точках, то все точки бюджетной линии между ними будут более предпочтительны для потребителя. И лишь в том только случае, если кривая безразличия имеет одну и только одну общую точку с бюджетной линией (точка Е на рис. 5), эта точка соответствует наиболее предпочтительному для потребителя набору товаров из всего множества доступных этому потребителю наборов. Точка Е называется точкой потребительского оптимума, поскольку расположена на наиболее высоко лежащей из доступных потребителю кривых безразличия, т.е. соответствует наиболее высокому уровню удовлетворения при данных доходе потребителя и ценах товаров.

Как известно, наклоны двух линий в точке их касания равны. Следовательно, в точке Е наклон бюджетной линии равен наклону кривой безразличия.

Вспомним теперь, что наклон кривой безразличия в данной точке равен предельной норме замены MRS, а наклон бюджетной линии - соотношению цен товаров P_X/P_Y. Следовательно, в точке потребительского оптимума Е

MRS = P_X/P_Y                                                                                (8)

Это свойство оптимального набора может быть легко объяснено логически. В самом деле, предельная норма замены MRS отражает то соотношение, в котором потребитель желает обменивать товар Y на товар X, точнее говоря, MRS показывает, какое количество единиц товара У потребитель согласен отдать, чтобы получить одну дополнительную единицу товара X. С другой стороны, соотношение цен P_X/P_Y характеризует пропорцию, в которой потребитель в действительности может обменивать товар Y на товар X, т. е. показывает, сколькими единицами товара Y должен пожертвовать потребитель, чтобы приобрести на рынке одну дополнительную единицу товара X.

Представим себе теперь, что в некоторой точке MRS > P_X/P_Y, т. е. потребитель готов отдать за дополнительную единицу товара Х больше единиц товара Y, чем это требует рынок. Эта точка не может быть точкой потребительского оптимума, поскольку потребитель будет стремиться увеличить уровень своего удовлетворения, замещая товар Y товаром X. Аналогичным образом, если MRS < P_X/P_Y, потребитель будет стремиться замещать товар Х товаром Y. И только в точках, подобных точке Е (рис. 5), где MRS =P_X/P_Y, а значит, индивидуальная норма замещения равна рыночной норме замещения, потребитель не имеет стимулов для изменения соотношения товаров в потребляемом наборе. Любое отклонение от этого состояния ведет к снижению уровня удовлетворения потребителя. По этой причине точку потребительского оптимума часто называют точкой равновесия потребителя.

Всегда ли, однако, точка потребительского оптимума характеризуется выражением (8)? Для ответа на этот вопрос рассмотрим различные типы карт безразличия.

1. Кривые безразличия не достигают осей координат, а асимптотически приближаются к ним или к иным прямым, параллельным осям координат (рис. 6). Это означает, что сколь бы ни был велик объем потребления одного из товаров, он все же не может компенсировать полное отсутствие другого товара в наборе (иначе говоря, ни один из товаров не может быть полностью заменен другим, т. е. потребитель не может обойтись без какого-то количества каждого из товаров).

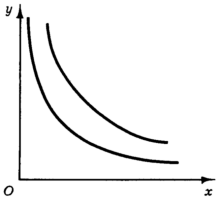
Рис. 6. Кривые безразличия не касаются осей координат

В этом случае при движении вдоль кривой безразличия норма замещения изменяется от нуля до бесконечности, и каково бы ни было соотношение цен P_X/P_Y, точка равновесия будет отвечать условию (8).

2. Кривые безразличия имеют общие точки с одной или обеими осями координат (рис. 7), т. е. потребитель может полностью отказаться от некоторого товара, компенсируя этот отказ увеличенным потреблением другого. При этом может оказаться, что на всей кривой безразличия MRS > P_X/P_Y или MRS < P_X/P_Y.

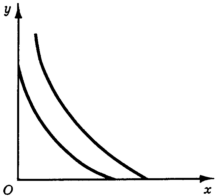
Рис. 7. Кривые безразличия имеют общие точки с осями координат

Где же будет в этих случаях располагаться точка потребительского оптимума? Рассмотрим рис. 8,а.

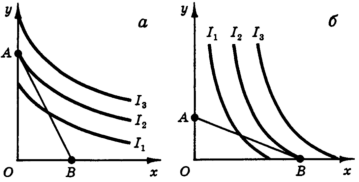
Рис. 8. Угловые положения потребительского оптимума

Очевидно, что потребитель достигает наивысшей из доступных кривых безразличия в точке А, где MRS < P_X/P_Y, и расходует все свои денежные средства исключительно на приобретение товара Y (х = 0). Товар Х оказывается слишком дорогим для данного потребителя. На рис. 8,б показан случай, когда потребитель расходует все денежные средства на товар X, и в точке потребительского оптимума MRS > P_X/P_Y.

Точки А (рис. 8,а) и В (рис. 8,б) носят название углового решения задачи потребительского выбора в противоположность внутреннему решению (точка Е на рис. 5). Отметим, что если для двухтоварного случая угловое решение является некой особой ситуацией, то для случая достаточно большого числа товаров угловое решение представляет собой скорее правило, чем исключение: ведь никто в самом деле не приобретает все те товары, которые предлагает ему рынок. Все же, оставаясь в рамках двухтоварной модели, мы будем в дальнейшем рассматривать главным образом внутреннее решение, считая выражение (8) условием оптимума потребителя. В разделе 2 мы перейдем к решению следующей задачи, стоящей перед теорией поведения потребителя, — изучить, как изменяется оптимум потребителя при изменении границ множества доступных данному потребителю наборов товаров, т. е. при изменении дохода и цен.

РАЗДЕЛ 2.

2.1 Реакция потребителя на изменение дохода

Итак, при некотором заданном доходе и заданных ценах потребитель однозначно определяет свои расходы - выбирает на бюджетной линии точку, которая соответствует самой "полезной" кривой безразличия. А что произойдет, если изменится доход и, следовательно, изменятся покупательные возможности потребителя? При неизменных ценах это выразится в параллельном сдвиге бюджетной линии. В случае увеличения дохода она отодвинется от начала координат и потребителю станут доступны более далекие кривые безразличия, а в случае уменьшения приблизится к началу координат и потребителю придется перейти на меньший уровень полезности.

На каждом уровне дохода потребитель будет выбирать самый полезный набор благ, и можно сказать, что каждой бюджетной линии соответствует своя оптимальная точка. Если мы рассмотрим все возможные уровни дохода и соединим все точки выбора, соответствующие каждому уровню, то мы получим линию доход-потребление. По ней движется потребитель при изменении своего дохода (рис. 1).

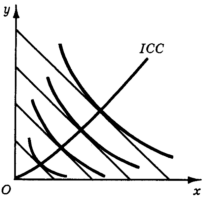
Рис. 1. Кривая доход-потребление

Х - питание, а y – одежда

На основании линии доход-потребление можно построить график доход-расходы для отдельного блага. На горизонтальной оси будем откладывать величину дохода, а на вертикальной - денежную сумму расходов на данное благо (рис. 2). Кривые такого типа называют кривыми Энгеля - по имени немецкого статистика XIX в. По характеру кривых Энгеля можно судить об отношении потребителя к благам: c ростом дохода кривая расходов на питание теряет наклон - спрос насыщается, а кривая расходов на одежду становится все круче - почти все приращение дохода уходит на одежду. Эта зависимость была видна на линии доход-потребление (рис. 1).

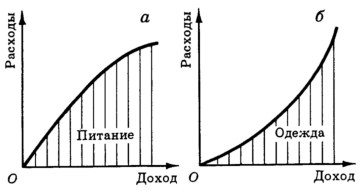
Рис. 2. Кривые доход-расходы на питание (а) и одежду (б).

Отметим, однако, что с увеличением дохода потребитель покупает больше и пищи, и одежды. В таких случаях экономисты говорят, что продукты питания и одежда являются нормальными товарами с точки зрения потребителя.

Если же объем закупок некоторого товара падает при увеличении потребительского дохода, то такой товар носит название низшего блага (англ. interior good). Например, большинство хозяек с увеличением дохода предпочитают использовать при приготовлении пищи все меньше дешевого маргарина, заменяя его более дорогим (но, по общему мнению, и более привлекательным) сливочным маслом.

Следует подчеркнуть, что один и тот же товар может быть низшим благом для одного потребителя и нормальным товаром для другого. Так, если потребитель рассматривает чай лишь как дешевый заменитель кофе, то с ростом дохода он будет, естественно, сокращать закупки чая, заменяя его кофе, и чай окажется низшим благом. В то же время для другого потребителя, который пьет чай потому, что ему это нравится, чай не будет низшим благом.

Но даже и для одного потребителя один и тот же товар может являться нормальным при одном уровне дохода и низшим благом при другом уровне. Рассмотрим потребителя, который любит и кофе, и чай, но все же в некоторой степени предпочитает кофе: при небольшом уровне дохода чай будет являться для этого потребителя нормальным товаром, однако с ростом дохода, когда кошелек сможет выдержать переход потребителя на кофе, чай рискует оказаться низшим благом

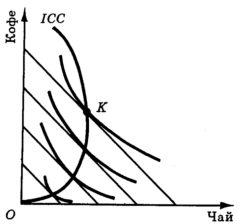
Рис. 3. Линия доход-потребление (чай - низшее благо).

На рис. 3 представлена линия доход-потребление некоторого потребителя для случая чай-кофе. Легко заметить, что эта линия на участке выше точки К поворачивает в направлении уменьшения потребления чая (в отличие от линий доход-потребление для пищи и одежды, изображенной на рис. 2). Такой поворот линии доход-потребление на рис. 3 означает, что при уровне дохода потребителя, превышающем уровень, для которого оптимальной комбинацией кофе и чая является набор K, чай становится низшим благом. На основе рис. 3 можно построить кривую Энгеля для расходов на чай (рис. 4).

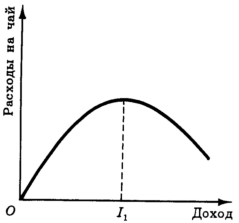
Рис. 4. Чай - нормальный товар при доходе меньшем, чем I₁, низшее благо при доходе выше I₁.

Перейдем теперь к весьма важному свойству кривых Энгеля: оказывается, кривые расходов на все потребляемые товары могут быть представлены на одном графике. Как это сделать? Проведем на плоскости доход-расходы линию, на которой расходы равны доходу. Как известно из курса математики, эта линия - биссектриса центрального угла (рис. 5). На рис. 6 эта линия показана прерывистой линией. Так как мы считаем, что потребитель весь свой доход тратит на приобретение товаров, данная линия представляет собой линию суммарных расходов потребителя на все приобретаемые товары.

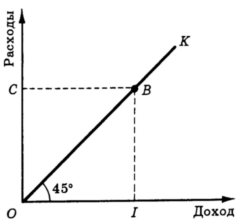
Рис. 5. Биссектриса координатного угла

Пусть потребитель (как и в начале настоящего раздела) покупает два продукта - пищу и одежду. Изобразим на рис. 6 кривую расходов на питание. Ордината любой точки на этой кривой показывает, как известно, величину расходов на питание при данном уровне дохода потребителя. Так, I₁F₁ - расходы на питание при доходе I₁. В то же время I₁G₁, - величина суммарных расходов потребителя при доходе I₁, (исходя из рассмотренных свойств линии ОK). Тогда что же показывает отрезок F₁G₁? Очевидно, F₁G₁ = I₁G₁ - I₁F₁ -величина расходов потребителя на одежду. Аналогичные рассуждения можно провести для любого уровня потребительского дохода (например, для дохода I₂: I₂F₂ - расходы на питание; I₂G₂ - суммарные расходы; F₂G₂ - расходы на одежду). Таким образом, на рис. 6 мы можем одновременно видеть, как изменяются при изменении дохода и расходы на питание, и расходы на одежду.

Рис. 6. Расходы на питание, одежду и суммарные расходы потребителя

А что если выйти за рамки нашего двухмерного случая в реальный мир, где потребитель покупает не два, а гораздо большее число товаров? И в этом случае расходы на все товары могут быть представлены на одном графике (рис. 7), построенном по тому же принципу, что и рис. 6.

бюджетный доход потребитель цена

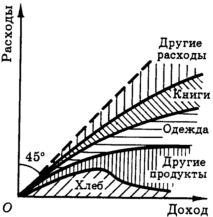
Рис. 7. Распределение потребительских расходов по статьям

Заметим, что в теории потребления мы все время предполагаем, что потребитель весь свой доход тратит на приобретение различных товаров. В действительности же потребитель при некотором уровне дохода может делать сбережения. В этом случае доходы потребителя будут превышать расходы на величину сбережений (рис. 8). С другой стороны, при низком уровне дохода потребитель вынужден брать деньги в долг, чтобы свести концы с концами. Эта ситуация представлена на рис. 9.

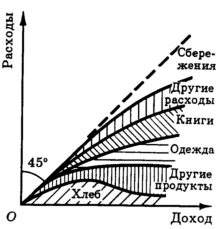
Рис. 8. Появление сбережений после некоторого уровня дохода

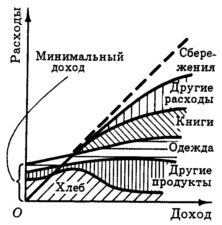
Рис. 9. При низком доходе потребитель вынужден занимать, при высоком - может сберегать

2.2 Реакция потребителя на изменение цен

Если изменение дохода при постоянных ценах выражалось в параллельных сдвигах бюджетной линии (рис. 1), то изменение цены на один из товаров при постоянстве дохода и цены другого товара будет выглядеть как поворот бюджетной линии (рис. 10). Таким образом, каждому значению цены товара Х будет соответствовать своя бюджетная линия, а каждой бюджетной линии - своя точка касания с какой-нибудь кривой безразличия. Соединив все эти точки выбора, как в предыдущем разделе, мы получим линию цена-потребление товара X.

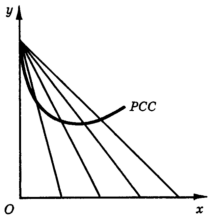
Рис. 10. Построение линии цена-потребление товара Х

То же самое можно проделать и для цены другого товара, появится линия цена-потребление товара Y (рис. 11). Обе линии характеризуют изменение потребительского выбора при изменении цен товаров Х и Y, по ним потребитель движется при повышении или понижении цены одного из товаров. Но каким образом происходит это движение? Необходимо помнить, что потребитель всегда находится на пересечении этих линий в точке А (рис. 12). Но обе эти линии не просто пересекаются, они "выходят" из этой точки. Это гипотетические дорожки, по которым будет двигаться потребитель в случае изменения одной из цен. Причем, когда он будет перемещаться по одной линии, другая в это время будет двигаться за ним как приклеенная (рис. 13). Обе линии всегда должны выходить из той точки, где находится потребитель.

Рис. 12. Кривые цена-потребление для товара Х (I), товара Y (II) и кривая доход-потребление (III).

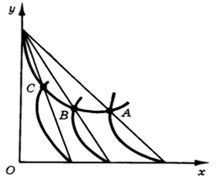
Рис. 13. Движение по одной из кривых цена-потребление.

Необходимо также отметить, что линия доход-потребление тоже выходит из этой точки (рис. 12). Это третья дорожка возможного движения потребителя при прочих равных. По ней он начнет перемещаться в случае изменения дохода. Но в реальной действительности эти траектории могут никогда не реализоваться, всегда существуя гипотетически.

На основе линии цена-потребление (где изменяется цена товара X) можно построить график зависимости объема потребления товара Х от его цены (рис. 14, а). Это есть не что иное, как кривая спроса. Аналогичным способом можно построить кривую спроса на товар Y (рис. 14, б). При повышении или снижении цены одного товара будет изменяться потребление не только этого, но и других товаров. Эту связь между кривыми спроса разберем на примере падения одной из цен, а именно снижения цены товара Х при постоянстве цены товара Y.

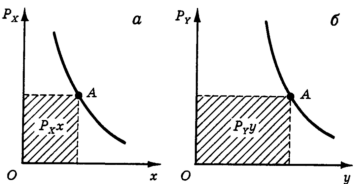
Рис. 14. Кривая спроса для товара Х (а) и для товара Y (б)

Площадь заштрихованного прямоугольника обозначает сумму расходов на товар

Итак, потребитель находится в точке А (рис. 15, а), покупая в единицу времени x₀ товара Х по цене и y₀ товара Y по цене (рис. 15, б). Когда цена Х внезапно падает с до , у потребителя появляется лишняя сумма денег, которой он может распорядиться. Этот выигрыш потребителя не зависит от формы кривой спроса, он полностью определяется исходным объемом потребления x0 и величиной падения цены (-). Но кривая спроса показывает, как он распределит высвободившуюся сумму. Посмотрите на рис. 15, а. Потребитель увеличивает расходы на товар X, переходя по кривой спроса из точки А в точку В. Заштрихованные площади на рис. 15, а показывают уменьшение расходов из-за снижения цены и их увеличение, связанное с покупкой дополнительного количества товара X.

Рис. 15. Последствия снижения цены товара X: движение вдоль кривой спроса на товар X (а) и сдвиг кривой спроса на товар Y (б). Случай низкоэластичного спроса на товар X.

А как это изменение изобразится на втором графике (рис. 15,б)?

Это выразится не в движении вдоль кривой спроса на товар Y - его цена остается прежней. Изменение цены на товар Х изображается сдвигом кривой спроса на товар Y. Но в какую сторону?

Если эластичность спроса на товар Х по абсолютной величине меньше единицы, то расходы потребителя на приобретение дополнительного количества товара Х меньше его выигрыша за счет снижения цены, и в целом его расходы на приобретение товара Х уменьшатся. Остальная часть его выигрыша пойдет на увеличение покупки товара Y, и кривая спроса сместится вправо. Площадь заштрихованного прямоугольника на рис. 15,б показывает дополнительные расходы на товар Y.

Но если спрос на товар Х высокоэластичен (эластичность по абсолютной величине больше единицы), то произойдет иначе. Расходы на покупку товара Х возрастут, и потребителю придется сократить расходы на покупку товара Y, а следовательно, уменьшить объем его потребления. Кривая спроса сместится влево (рис. 16,б).

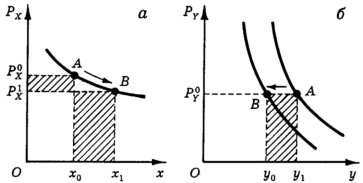
Рис. 16. Тот же процесс, что и на рис 15.Случай высокоэластичного спроса на товар Х

Но эластичность не остается постоянной на всем протяжении кривой спроса. На рис. 17 показана линейная функция спроса на товар X. Участок I характеризуется высокой эластичностью, и при снижении цены товара Х на этом участке кривая спроса на товар Y сдвигается влево. Но в точке В эластичность становится единичной и при дальнейшем движении продолжает снижаться, а кривая спроса на товар Y начинает смещаться вправо (участок II).

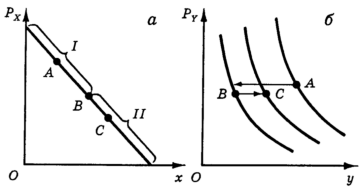
Рис. 17. Кривая спроса на товар Х имеет высокую эластичность на участке I и низкую эластичность на участке II. Тот же процесс, что на рис. 15, 16

Аналогично можно рассмотреть падение цены другого товара и повышение каждой из цен.

2.3 Кривые Энгеля

Распределение потребителем своего бюджета можно исследовать не только исходя из теоретических предпосылок (как мы это делали раньше), но и эмпирически - проследить, какие решения принимают в тех или иных случаях реальные потребители.

Как это сделать?

В принципе можно просто попросить их мысленно оценить свой выбор в тех или иных условиях (при меняющихся доходе или ценах) и на основе их ответов построить кривые типа "если-то", характеризующие предпочтения конкретных потребителей. Но здесь есть серьезное препятствие. Совпадет ли мысленная оценка с выбором в реальных условиях? Попробуйте ответить на вопрос: как бы вы распределили свой доход, если бы он вырос в два, пять, десять раз?

Для получения правильных данных и построения кривых Энгеля или кривых спроса нужно провести эксперимент. Однако искусственные эксперименты такого рода тоже весьма трудно осуществимы. Представим себе, что в нашем городе нужно методично и спокойно повышать каждую неделю цену на хлеб или каждый месяц уменьшать доходы и смотреть, как мечутся и волнуются потребители ради нашего научного любопытства. Или понижать цену на молоко и повышать доходы, а на самом интересном месте объявить, что эксперимент закончился!

Но если посмотреть повнимательнее, мы можем увидеть, что все-таки один "эксперимент" уже произошел сам собой, естественным образом, и позволяет нам построить кривые Энгеля.

Если выбрать несколько потребителей, которые сталкиваются с одинаковыми продуктами и ценами, но имеют разные доходы, и зафиксировать их расходы, то у нас появится возможность исследовать изменение потребления в связи с изменением дохода.

Их можно рассматривать как одного и того же потребителя, помещаемого в одну и ту же систему, но каждый раз с другим доходом. Поэтому, нанеся их расходы на питание, одежду и т. д. на график, можно получить кривые Энгеля. А если мы во время исследования постараемся захватить представителей разных имущественных слоев, у нас получится как бы вертикальный срез целого общества (рис. 7) - картинка, показывающая, кто, сколько и чего потребляет в момент исследования, и изображающая реакцию людей на изменение дохода.

В этих кривых есть свой смысл. Самым разным людям присущи общие культурные и психологические закономерности поведения. И подобные исследования позволяют сделать общие выводы о характере потребления среднего человека при данном ассортименте продуктов и системе цен. А насколько эти общие тенденции свойственны каждому из людей - тема для интересной дискуссии.

Обратившись к истории, увидим, что изучение потребления на основе бюджетной статистики началось задолго до появления графического аппарата его анализа.

Сама бюджетная статистика, как сбор фактического материала, зародилась в Англии в самом конце XVIII в., хотя ученые того времени не подозревали, какое развитие может получить эта тема в дальнейшем. Первые исследования были связаны с голодом и бедствиями рабочих после неурожая 1794-1795 гг.: нужно было узнать, как живут люди. Под влиянием этой же причины стали появляться бюджетные исследования и в других странах Западной Европы. Но еще полстолетия это был только сбор статистического материала, пусть все более и более хорошо