Реакторы идеального вытеснения
Кафедра основ Химической Технологии
КОНТРОЛЬНАЯ РАБОТА
по теме
«Реакторы идеального вытеснения»
Вариант № 14
реактор газовый поток вытеснение
В Р.И.В. Проводят окисление SO2. Объем реакционной зоны 150 м2. Объемный расход смеси 50000 м3/г. Состав исходной смеси SO2 – 0,1; O2 – 0,11; SO3 – 0,01; остальное – азот. Давление в реакторе Р=1,5 атм.
Определить значение температуры газового потока на входе в реакторе, обеспечивающее максимальную производительность реактора.
SO2 + ½ O2 = SO3

![]() ;
; ![]() ;
; ![]()
 ;
; ![]()
Теплоемкости: ![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]()
Введение
Степень перемешивания реагирующих масс в реакторах непосредственно влияет на режим их работы. При идеальном вытеснении температура изменяется по высоте реакционного объема и в результате меняется константа скорости реакции и, соответственно, скорость процесса.
В Р.И.В. все частицы движутся в заданном направлении, не перемешиваясь с движущимися впереди и сзади, и полностью вытесняя подобно поршню находящиеся впереди частицы потока. Временно характеристикой Р.И.В. служит уравнение:
![]()
А также:
![]()
Если рассматривать процесс, протекающий в элементарном объеме реактора за время, то приход реагента в этот объем может быть представлен как:
![]()
Убыль (расход):
![]()
Количество исходного реагента, расходуемого на химическую реакцию:
![]()
Уравнение материального баланса всего реактора:
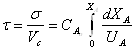 (*)
(*)
Уравнение (*) представляет собой характеристическое уравнение Р.И.В. Оно позволяет, если известна кинетика процесса, определить время пребывания реагентов, а затем и размеры реактора при заданных расходе реагентов и степени превращения или производительности реактора или при заданных размерах реактора и степени превращения.
Модель вытеснения можно применять для технических расчетов при проектировании жидкофазных трубчатых реакторов и для расчета камерных печей.
Программа для расчета, составляется в приложении REAC
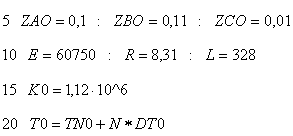

-процедура решения дифференциального уравнения ![]() , параметры процедуры:
, параметры процедуры:
искомая функция ٱXٱ по аргументу ٱTAUٱ !
начальное значение аргумента ٱOٱ конечное значение аргумента ٱTAUkٱ!
идент-р. произв. ٱFٱ начальных значений функции ٱОٱ !
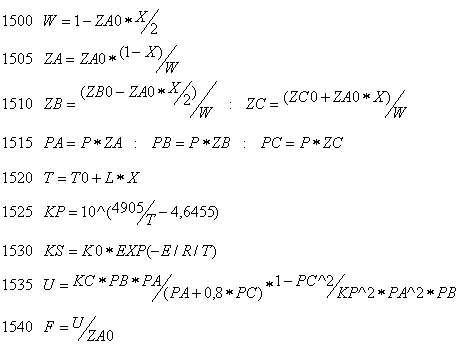
![]()
Результаты расчетов:
| Tо | Y |
| 600 | 899,129 |
| 625 | 984,872 |
| 650 | 1069,380 |
| 675 | 1141,420 |
| 700 | 1199,770 |
| 725 | 1242,670 |
| 750 | 1270,040 |
| 775 | 1281,800 |
| 800 | 1277,890 |
| 825 | 1258,640 |
| 850 | 1225,190 |
| 875 | 1177,820 |
| 900 | 1117,850 |
| 925 | 1046,690 |
Подобные работы: