Уравнения смешанного типа
В современной теории дифференциальных уравнений с частными производными важное место занимают исследования вырождающихся гиперболических и эллиптических уравнений, а также уравнений смешанного типа. Уравнения смешанного типа стали изучаться систематически с конца 40-х годов, после того, как Ф.И. Франкль указал их приложения в околозвуковой и сверхзвуковой газовой динамике. Позже И.Н. Векуа были найдены приложения этих уравнений и в других разделах физики и механики, в частности, в теории бесконечно малых изгибаний поверхностей и безмоментной теории оболочек. Также повышенный интерес к этим классам уравнений объясняется как теоретической значимостью полученных результатов, так и их многочисленными приложениями в гидродинамике, в различных разделах механики сплошных сред, акустике, в теории электронного рассеяния и многих других областях знаний. Исследования последних лет также показали, что такие уравнения являются основой при моделировании биологических процессов.
Начало исследований краевых задач для уравнений смешанного типа было положено в работах Ф. Трикоми и С. Геллерстедта. В дальнейшем основы теории уравнений смешанного типа были заложены в работах Ф.И. Франкля, А.В. Бицадзе, К.И. Бабенко, С. Агмона, Л. Ниренберга, М. Проттера, К. Моравец и многих других авторов. Результаты, полученные ими и их последователями приведены в монографиях А.В. Бицадзе (4), Л. Берса (2), К.Г. Гудейлея (6), Т.Д. Джураева (7), М.М. Смирнова (14), Е.И. Моисеева (9), К.Б. Сабитова (12), М.С. Салахитдинова (13).
Среди краевых задач особое место занимают нелокальные задачи. Нелокальные задачи для дифференциальных уравнений рассматривались в работах Ф.И. Франкля (15), А.В. Бицадзе и А.А. Самарского (3), В.А. Ильина, Е.И. Моисеева, Н.И. Ионкина, В.И. Жегалова (8), А.И. Кожанова, А.М. Нахушева, Л.С. Пулькиной (10), О.А. Репина (11), А.Л. Скубачевского, А.П. Солдатова и других.
Особо выделим работу А.В. Бицадзе и А.А. Самарского (3), которая повлекла за собой систематическое изучение нелокальных краевых задач для эллиптических и других типов уравнений.
Первые фундаментальные исследования вырождающихся гиперболических уравнений были выполнены Ф. Трикоми в начале прошлого столетия. Для уравнения
![]() (0.1)
(0.1)
он поставил следующую задачу: пусть ![]() область, ограниченная при
область, ограниченная при ![]() гладкой кривой
гладкой кривой ![]() с концами в точках
с концами в точках ![]() и
и ![]() оси
оси ![]() а при
а при ![]() характеристиками
характеристиками ![]() уравнения (0.1). Требуется найти функцию
уравнения (0.1). Требуется найти функцию ![]() (
(![]() отрезок оси
отрезок оси ![]() ), удовлетворяющую уравнению (0.1) в
), удовлетворяющую уравнению (0.1) в ![]() и принимающую заданные значения на
и принимающую заданные значения на ![]() Ф. Трикоми доказал существование и единственность решения этой задачи при определённых дополнительных требованиях относительно поведения
Ф. Трикоми доказал существование и единственность решения этой задачи при определённых дополнительных требованиях относительно поведения ![]() в
в ![]() гладкости граничных данных и характера дуги
гладкости граничных данных и характера дуги ![]() . Эта краевая задача и уравнение (0.1) называются сейчас задачей и уравнением Трикоми.
. Эта краевая задача и уравнение (0.1) называются сейчас задачей и уравнением Трикоми.
М.А. Лаврентьев с целью упрощения исследований краевых задач для уравнений смешанного типа предложил новое модельное уравнение
![]() (0.2)
(0.2)
Подробное исследование задачи Трикоми и её различных обобщений для уравнения (0.2) провёл А.В. Бицадзе. Уравнение (0.2) называют сейчас уравнением Лаврентьева-Бицадзе.
Нахушев А.М. установил критерий единственности решения задачи Дирихле для уравнений смешанного типа в цилиндрической области .
В работах Сабитова К.Б. исследована задача Дирихле для вырождающегося уравнения смешанного типа
![]()
в прямоугольной области. Методами спектрального анализа установлен критерий единственности и доказана теорема существования решения задачи Дирихле.
Изложенный в работах Е.И. Моисеева, К.Б. Сабитова спектральный метод применён при обосновании корректности постановки нелокальных начально-граничных и граничных задач для различных типов вырождающихся дифференциальных уравнений.
Целью данной работы является доказательство единственности и существования решения следующих задач:
Рассмотрим вырождающееся уравнение
![]() (0.3)
(0.3)
где ![]() в прямоугольной области
в прямоугольной области ![]()
![]() заданные положительные числа, и для него исследуем следующую нелокальную задачу.
заданные положительные числа, и для него исследуем следующую нелокальную задачу.
Задача 1. Найти в области ![]() функцию
функцию ![]() , удовлетворяющую условиям:
, удовлетворяющую условиям:
![]() ; (0.4)
; (0.4)
![]() ; (0.5)
; (0.5)
![]() (0.6)
(0.6)
![]() (0.7)
(0.7)
где ![]() и
и ![]()
![]() заданные достаточно гладкие функции, причём
заданные достаточно гладкие функции, причём ![]()
Для того же уравнения исследована и следующая задача:
Задача 2. Найти в области ![]() функцию
функцию ![]() , удовлетворяющую условиям:
, удовлетворяющую условиям:
![]() (0.8)
(0.8)
![]() ; (0.9)
; (0.9)
![]() (0.10)
(0.10)
![]() (0.11)
(0.11)
где ![]() и
и ![]() – заданные достаточно гладкие функции, причём
– заданные достаточно гладкие функции, причём
![]() ,
, ![]()
![]() ,
, ![]()
Для указанных задач установлены критерии их однозначной разрешимости. Решения получены явно в виде соответствующих рядов.
1. Нелокальная граничная задача Ι рода
Рассмотрим вырождающееся уравнение смешанного типа
![]() (1)
(1)
где ![]() в прямоугольной области
в прямоугольной области ![]() заданные положительные числа, и для него исследуем следующую нелокальную задачу.
заданные положительные числа, и для него исследуем следующую нелокальную задачу.
Задача 1. Найти в области ![]() функцию
функцию ![]() , удовлетворяющую условиям:
, удовлетворяющую условиям:
![]() ; (2)
; (2)
![]() ; (3)
; (3)
![]() (4)
(4)
![]() (5)
(5)
где ![]() и
и ![]()
![]() заданные достаточно гладкие функции, причём
заданные достаточно гладкие функции, причём ![]()
Пусть ![]() решение задачи (2)
решение задачи (2) ![]() Рассмотрим функции
Рассмотрим функции
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
Дифференцируя дважды равенство (8), учитывая уравнение (1) и условия (4), получим дифференциальное уравнение
![]() (9)
(9)
с граничными условиями
![]() , (10)
, (10)
![]() (11)
(11)
Общее решение уравнения (9) имеет вид
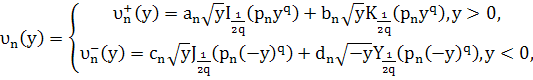
где ![]() и
и ![]() функции Бесселя первого и второго рода соответственно,
функции Бесселя первого и второго рода соответственно,![]() модифицированные функции Бесселя,
модифицированные функции Бесселя, ![]() и
и ![]() произвольные постоянные,
произвольные постоянные, ![]()
Подберём постоянные ![]() и
и ![]() так, чтобы выполнялись равенства
так, чтобы выполнялись равенства
![]() (13)
(13)
Опираясь на асимптотические формулы функций Бесселя
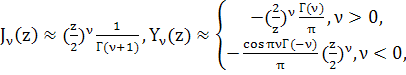
и модифицированных функций Бесселя
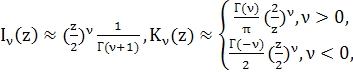
в окрестности нуля, первое из равенств (13) выполнено при ![]() и любых
и любых ![]() и
и ![]() , а второе равенство выполнено при
, а второе равенство выполнено при
![]()
Подставим полученные выражения для постоянных ![]() и
и ![]() в (12), тогда функции
в (12), тогда функции ![]() примут вид
примут вид
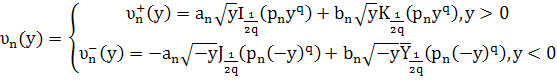
![]()
Отметим, что для функций (14) выполнено равенство
![]()
Отсюда и из равенств (13) вытекает, что ![]() является продолжением решения
является продолжением решения ![]() на промежуток
на промежуток ![]() и,наоборот,
и,наоборот, ![]() является продолжением решения
является продолжением решения ![]() на промежуток
на промежуток ![]() . Следовательно, функции (14) принадлежат классу
. Следовательно, функции (14) принадлежат классу ![]() и удовлетворяет уравнению (9) всюду на
и удовлетворяет уравнению (9) всюду на ![]() . Теперь на основании (10) и (11) получим систему для нахождения
. Теперь на основании (10) и (11) получим систему для нахождения ![]() и
и ![]() :
:
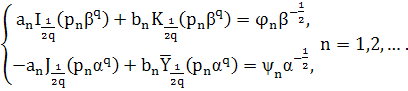 (15)
(15)
Если определитель системы (15):
![]() (16)
(16)
то данная система имеет единственное решение
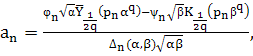 (17)
(17)
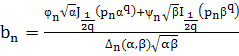 . (18)
. (18)
С учётом (17) и (18) из (14) найдём окончательный вид функций
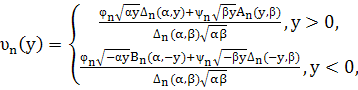 (19)
(19)
Где
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
Дифференцируя дважды равенство (7) с учётом уравнения (1) и условий (4) для функции ![]() , получим однородное дифференциальное уравнение
, получим однородное дифференциальное уравнение
![]() (24)
(24)
с граничными условиями
![]() (25)
(25)
Решение задачи (24) и (25) будет иметь вид
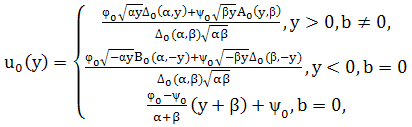 (26)
(26)
![]()
![]()
![]()
![]()
Аналогично для функции ![]() получаем неоднородное уравнение
получаем неоднородное уравнение
![]() (27)
(27)
с граничными условиями
![]() (28)
(28)
![]() (29)
(29)
Общее решение уравнения (27) имеет вид
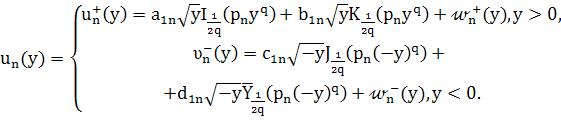
Равенства ![]() будут выполняться при следующих значениях постоянных
будут выполняться при следующих значениях постоянных
![]() ,
, ![]()
при любых ![]() и
и ![]() Подставим выражения для постоянных
Подставим выражения для постоянных ![]() и
и ![]() в (30), тогда функции
в (30), тогда функции ![]() примут вид
примут вид
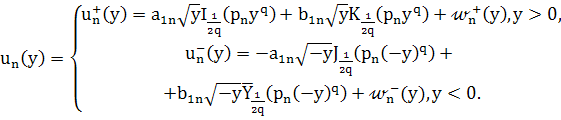 (31)
(31)
Для нахождения ![]() и
и ![]() на основании (28) и (29) получим систем
на основании (28) и (29) получим систем
 (32)
(32)
Если выполнено условие (16), то ![]() и
и ![]() определяются по формулам:
определяются по формулам:
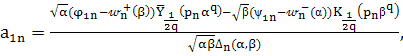 (33)
(33)
 , (34)
, (34)
Найденные значения ![]() и
и ![]() по формулам (33) и (34) подставим в (31), тогда функции
по формулам (33) и (34) подставим в (31), тогда функции ![]() будут однозначно построены в явном виде:
будут однозначно построены в явном виде:
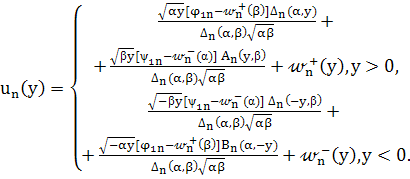 (35)
(35)
Из формул (19), (26), (35) следует единственность решения задачи (2)![]() так как если
так как если ![]()
![]() на
на ![]() , то
, то ![]() ,
, ![]() для
для ![]() на
на ![]() Тогда из (6)
Тогда из (6)![]() имеем:
имеем:
![]()
![]()
Отсюда в силу полноты системы
![]()
в пространстве ![]() следует, что функция
следует, что функция ![]() почти всюду на
почти всюду на ![]() при любом
при любом ![]() .
.
Таким образом, нами доказана следующая
Теорема 1. Если существует решение ![]() задачи (2)
задачи (2)![]() то оно единственно только тогда, когда
то оно единственно только тогда, когда ![]() при всех
при всех ![]()
Действительно, если выполнено условие (16) и решение задачи (2)![]() существует, то оно единственно. Пусть при некоторых
существует, то оно единственно. Пусть при некоторых ![]() и
и ![]() нарушено условие (16), т. е.
нарушено условие (16), т. е. ![]() Тогда однородная задача (2)
Тогда однородная задача (2)![]() (где
(где ![]() имеет нетривиальное решение
имеет нетривиальное решение
![]()
Выражение для ![]() на основании следующих формул
на основании следующих формул
![]()
приводим к виду
![]()

![]()
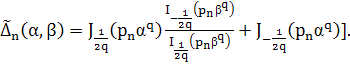
Поскольку при любом ![]() и
и ![]()
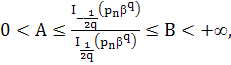
где ![]() и
и ![]() положительные постоянные, то функция
положительные постоянные, то функция
![]()
где ![]() в силу теоремы Хилби
в силу теоремы Хилби ![]() имеет счётное множество положительных нулей.
имеет счётное множество положительных нулей.
Следовательно, ![]() при некоторых
при некоторых ![]() может иметь счётное множество нулей независимо от
может иметь счётное множество нулей независимо от ![]() . Поскольку
. Поскольку ![]() любое положительное число ,то оно может принимать значения, близкие к нулям
любое положительное число ,то оно может принимать значения, близкие к нулям ![]() Поэтому при больших n выражение
Поэтому при больших n выражение![]() может стать достаточно малым, т.е. возникает проблема
может стать достаточно малым, т.е. возникает проблема ![]() Чтобы такой ситуации не было, надо показать существование
Чтобы такой ситуации не было, надо показать существование ![]() и
и ![]() таких, что при любом
таких, что при любом ![]() и больших
и больших ![]() справедлива оценка
справедлива оценка
![]()
Представим (16) в следующем виде
![]() (36)
(36)
где
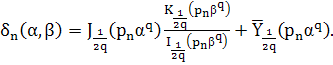
Как известно ![]() функция
функция ![]() строго убывает, функция
строго убывает, функция ![]() строго возрастающая по
строго возрастающая по ![]() , поэтому величина
, поэтому величина
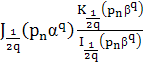
есть бесконечно малая более высокого порядка, чем ![]() при больших
при больших ![]() . Поэтому рассмотрим только выражение
. Поэтому рассмотрим только выражение
![]()
Используя асимптотическую формулу функции ![]() при
при ![]()
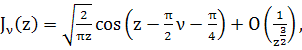
Получаем
![]()
![]()
Где
![]()
Отсюда видно, что если, например,![]() где
где ![]() то при
то при ![]()
![]()
Тем самым справедлива следующая
Лемма 1. Существует ![]() и постоянная
и постоянная ![]() такие, что при всех
такие, что при всех ![]() и больших
и больших ![]() справедлива оценка
справедлива оценка
![]() (37)
(37)
Рассмотрим следующие отношения:
![]()
![]() ,
, ![]()
Лемма 2. При любом ![]() для достаточно больших n справедливы оценки:
для достаточно больших n справедливы оценки:
![]()
![]() ;
;
![]() ;
;
![]()
где ![]() ,
, ![]() здесь и в дальнейшем, положительные постоянные.
здесь и в дальнейшем, положительные постоянные.
Доказательство. С учётом (36) функция ![]() примет вид
примет вид
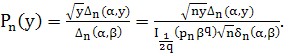
Оценим функцию ![]() при
при ![]() и больших
и больших ![]() :
:
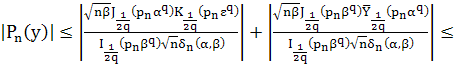
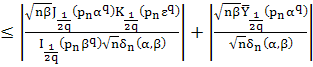 .
.
На основании поведений функций ![]() в окрестности бесконечно-удалённой точки и леммы 1, получим
в окрестности бесконечно-удалённой точки и леммы 1, получим
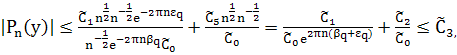 (38)
(38)
где ![]() здесь и далее произвольные постоянные.
здесь и далее произвольные постоянные.
При 0![]() и n>>1 в силу асимптотических формул имеем
и n>>1 в силу асимптотических формул имеем
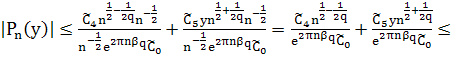
![]() (39)
(39)
Сравнивая (38) и (39) при любом ![]() получим
получим
![]()
Далее вычислим производную
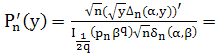
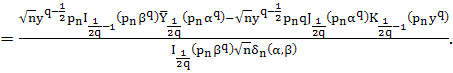
Оценим эту функцию при ![]() и больших
и больших ![]() :
:
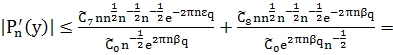
![]() (41)
(41)
При ![]() и больших фиксированных
и больших фиксированных ![]() имеем
имеем
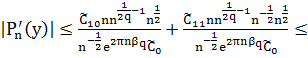
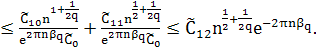 (42)
(42)
Из оценок (41) и (42) следует, что при всех ![]()
![]()
Вторую производную функции ![]() вычислим следующим образом:
вычислим следующим образом:
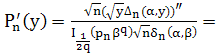

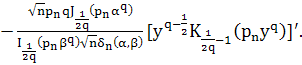
Используя формулы ((1), стр. 90)
![]()
Получаем
![]()
Зная оценку (40) для ![]() из последнего равенства при всех
из последнего равенства при всех ![]() имеем
имеем
![]()
Функция ![]() с учётом (36) примет вид:
с учётом (36) примет вид:
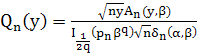 .
.
Оценим её, используя лемму 1 при 0![]() и больших n:
и больших n:
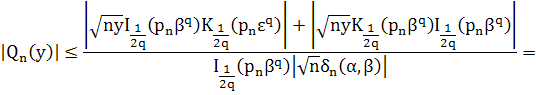
![]() (43)
(43)
При ![]() и больших фиксированных
и больших фиксированных ![]() :
:
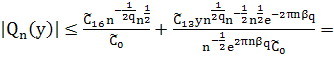
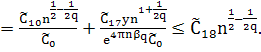 (44)
(44)
Из оценок (43) и (44) имеем:
![]() (45)
(45)
Вычислим производную ![]() :
:
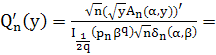
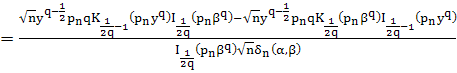 .
.
Оценим функцию ![]() при
при ![]() и
и ![]() :
:
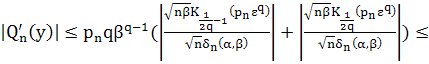
![]() (46)
(46)
При ![]() и
и ![]() имеем:
имеем:
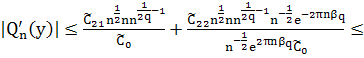
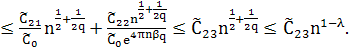 (47)
(47)
Сравнивая (46) и (47) при всех ![]() , получим
, получим
![]()
Теперь вычислим вторую производную функции
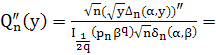

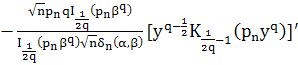
Используя формулы
![]()
Получим
![]()
Отсюда на основании оценки (45) будем иметь
![]() (48)
(48)
Аналогично получаем оценку для функции ![]() и
и ![]() :
:
![]()
![]()
Лемма 3. При любом ![]() для достаточно больших
для достаточно больших ![]() справедливы оценки:
справедливы оценки:
![]()
![]()
![]()
![]()
Доказательство. Используя ![]()
![]()
![]() и
и ![]() функцию
функцию ![]() , определяемую формулой (19), представим в следующем виде:
, определяемую формулой (19), представим в следующем виде:
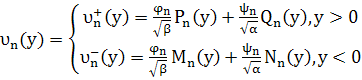 (49)
(49)
Из (49) в силу леммы 2 получим оценки для функций ![]()
![]() и
и ![]() Аналогичные оценки справедливы и для функций
Аналогичные оценки справедливы и для функций ![]()
![]() и
и ![]() Лемма доказана.
Лемма доказана.
Лемма 4. Пусть 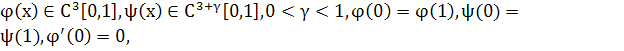
![]() то справедливы оценки:
то справедливы оценки:
![]()
![]() (50)
(50)
![]()
![]()
При получении оценок (50) дополнительно применяется теорема о скорости убывания коэффициентов ряда Фурье функции, удовлетворяющей на ![]() условию Гёльдера с показателем
условию Гёльдера с показателем ![]()
Теорема 2. Пусть 
![]() и выполнены условия (16) и (37). Тогда задача (2)-(5) однозначно разрешима и это решение определяется рядом
и выполнены условия (16) и (37). Тогда задача (2)-(5) однозначно разрешима и это решение определяется рядом
![]() (51)
(51)
где функции ![]() ,
,![]()
![]() определены соответственно по формулам (26), (35), (19).
определены соответственно по формулам (26), (35), (19).
Доказательство. Поскольку системы функций
![]()
![]()
образуют базис Рисса, то если ![]() , тогда функцию
, тогда функцию ![]() можно представить в виде биортогонального ряда (51), который сходится в
можно представить в виде биортогонального ряда (51), который сходится в ![]() при любом
при любом ![]() . В силу лемм 3 и 4 ряд (51) при любом
. В силу лемм 3 и 4 ряд (51) при любом ![]() из
из ![]() мажорируется сходящимся рядом
мажорируется сходящимся рядом
![]()
поэтому ряд (51) в силу признака Вейерштрасса сходится абсолютно и равномерно в замкнутой области ![]() . Следовательно, функция
. Следовательно, функция ![]() непрерывна на
непрерывна на ![]() как сумма равномерно сходящегося ряда (51). Ряды из производных второго порядка в
как сумма равномерно сходящегося ряда (51). Ряды из производных второго порядка в ![]() мажорируются также сходящимся числовым рядом
мажорируются также сходящимся числовым рядом
![]()
Поэтому сумма ![]() ряда (51) принадлежит пространству
ряда (51) принадлежит пространству ![]() и удовлетворяет уравнению (1) в
и удовлетворяет уравнению (1) в ![]() . Следствие 1. Построенное решение
. Следствие 1. Построенное решение ![]() задачи (2)-(5) принадлежит классу
задачи (2)-(5) принадлежит классу ![]() и функция
и функция ![]() всюду в
всюду в ![]() является решением уравнения (1). Следовательно, линия изменения типа
является решением уравнения (1). Следовательно, линия изменения типа ![]() уравнения (1) как особая линия устраняется.
уравнения (1) как особая линия устраняется.
2. Нелокальная граничная задача II рода
Рассмотрим уравнение (1) в прямоугольной области ![]() и исследуем сопряжённую относительно задачи 1 задачу.
и исследуем сопряжённую относительно задачи 1 задачу.
Задача 2. Найти в области ![]() функцию
функцию ![]() , удовлетворяющую условиям:
, удовлетворяющую условиям:
![]() (52)
(52)
![]() ; (53)
; (53)
![]() (54)
(54)
![]() (55)
(55)
где ![]() и
и ![]() – заданные достаточно гладкие функции, причём
– заданные достаточно гладкие функции, причём ![]() ,
, ![]()
![]() ,
, ![]()
Пусть ![]() решение задачи (52)- (55). Вновь воспользуемся системами
решение задачи (52)- (55). Вновь воспользуемся системами
![]()
![]()
Рассмотрим функции
![]() , (56)
, (56) ![]() (57)
(57)
![]() (58)
(58)
Дифференцируя дважды равенство (56) и учитывая уравнение (1), получим дифференциальное уравнение
![]() (59)
(59)
с граничными условиями
![]() (60)
(60)
![]() (61)
(61)
Следуя §1 решение задачи (59)-(61) построим в виде
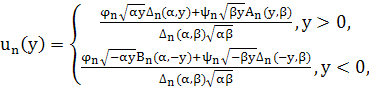 (62)
(62)
C учётом уравнения (1) продифференцируем дважды равенство (57). Получим для функции ![]() однородное дифференциальное уравнение
однородное дифференциальное уравнение
![]() (63)
(63)
с граничными условиями
![]() (64)
(64)
Решение задачи (63) и (64) имеет вид
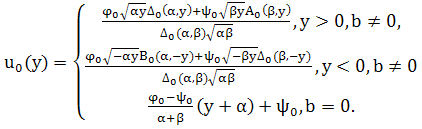 (65)
(65)
Дифференцируя дважды равенство (58) и учитывая уравнение (1) и условия (54), получаем неоднородное уравнение для функции ![]()
![]() (66)
(66)
с граничными условиями
![]() , (67)
, (67)
![]() . (68)
. (68)
Решение этой задачи определяется по формуле
 (69)
(69)
Из формул (62), (65), (69) следует единственность решения задачи (52)-(55), так как если ![]() на
на ![]() то
то ![]() ,
, ![]() ,
, ![]() для
для ![]() на
на ![]() Тогда из (56)-(58) имеем:
Тогда из (56)-(58) имеем:
![]() ,
, ![]() ,
,
![]()
Отсюда в силу полноты системы
![]()
в пространстве ![]() следует, что функция
следует, что функция ![]() почти всюду на
почти всюду на ![]() при любом
при любом ![]() .
.
Теорема 3. Если существует решение ![]() задачи (52)-(55), то оно единственно тогда и только тогда, когда при всех n выполняется условие (16).
задачи (52)-(55), то оно единственно тогда и только тогда, когда при всех n выполняется условие (16).
Действительно, если выполнено условие (16) и решение задачи (52)-(55) существует, то оно единственно. Пусть при некоторых ![]() и
и ![]() нарушено условие (16), т. е.
нарушено условие (16), т. е. ![]() . Тогда однородная задача (52)-(55) (где
. Тогда однородная задача (52)-(55) (где ![]() ) имеет нетривиальное решение
) имеет нетривиальное решение
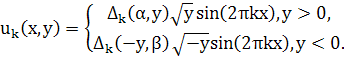
Теорема 4. Если ![]()
![]()
![]() ,
, ![]() и выполнены условия (16) и (37), то существует единственное решение задачи (52)-(55) и оно представимо в виде суммы ряда
и выполнены условия (16) и (37), то существует единственное решение задачи (52)-(55) и оно представимо в виде суммы ряда
![]()
![]()
где функции ![]() ,
, ![]() определены соответственно по формулам (65), (62), (69).
определены соответственно по формулам (65), (62), (69).
Доказательство теоремы 4 аналогично доказательству теоремы 2.
Следствие 2. Построенное решение ![]() задачи (52)-(55) принадлежит классу
задачи (52)-(55) принадлежит классу ![]() и функция
и функция ![]() всюду в
всюду в ![]() является решением уравнения (1). Следовательно, линия изменения типа
является решением уравнения (1). Следовательно, линия изменения типа ![]() уравнения (1) как особая линия устраняется.
уравнения (1) как особая линия устраняется.
Литература
1. Бейтмен, Г. Высшие трансцендентные функции / Г. Бейтмен, А. Эрдейн.![]() М.: Наука, 1966. Т.
М.: Наука, 1966. Т.![]()
2. Берс, Л. Математические вопросы дозвуковой и околозвуковой газовой динамики / Л. Берс. ![]() М.: ИЛ,
М.: ИЛ, ![]()
3. Бицадзе, А.В. О некоторых простейших обобщениях эллиптических задач/ А.В. Бицадзе, А.А. Самарский // Докл. АН СССР. – 1969. – Т. 185. – № 4. – С. 739 – 740.
4. Бицадзе, А.В. Некоторые классы уравнений в частных производных /
А.В. Бицадзе. – М.: Наука, 1981.– 448 с.
5. Ватсон, Г.Н. Теория бесселевых функций.I./ Г.Н. Ватсон.–М.: ИЛ, 1940.– 421 с.
6. Гудерлей, К.Г. Теория околозвуковых течений / К.Г. Гудерлей. – М.: ИЛ, 1960. – 421 с.
7. Джураев, Т.Д. Краевые задачи для уравнений смешанного и смешанно-составного типов /Т.Д. Джураев – М.: ИЛ, 1961. – 208 с.
8. Жегалов, В.И. Нелокальная задача Дирихле для уравнения смешанного типа / В.И. Жегалов // Неклассич. уравнения матем. физики. – Новосибирск: ИМ СО АН СССР. 1985. – С.172 с.
9. Моисеев, Е.И. Уравнения смешанного типа со спектральным параметром / Е.И. Моисеев. – М.: МГУ, 1988. – 150 с.
10. Пулькина, Л.С. Нелокальная задача с нелокальным условием для гиперболического уравнения / Л.С. Пулькина // Неклассич. уравнения матем. физики. Новосибирск: ИМ СО РАН, 2002. – С. 176 – 184 с.
11. Репин, О.А. Задача Трикоми для уравнения смешанного типа в области, эллиптическая часть которой – полуполоса / О.А. Репин // Дифференциальные уравнения. – 1996. – Т. 32, №4. – С. 565 – 567 с.
12. Сабитов, К.Б. К теории уравнений смешанного типа с двумя линиями изменения типа / К.Б. Сабитов, Г.Г. Биккулова, А.А. Гималтдинова – Уфа.: Гилем, 2006. – 150 с.
13. Салахитдинов, М.С. Уравнения смешанно-составного типа – М.С. Салахитдинов. – Ташкент: Фан, 1974. – 156 с.
14. Смирнов, М.М. Уравнения смешанного типа / М.М Смирнов. – М.: Высшая школа, 1985. – 304 с.
15. Франкль, Ф.И. Обтекание профилей потоком дозвуковой скорости со сверхзвуковой зоной, оканчивающейся прямым скачком уплотнения / Ф.И. Франкль // ПММ. – 1956. – Т. 20. – №2. – с. 196 –202 с.