Теория столкновений

В последние десятилетия наука об атомных явлениях образовала не только одну из важнейших глав современной физики, но и получила широкое применение в современной технике.

Уже самый поверхностный взгляд на область атомных явлений обнаруживает новые черты, существенно отличные от тех, которые свойственны микромиру.

Первое, с чем мы встречаемся в микромире – это атомизм. Простейшие, элементарные частицы характеризуются вполне определенными признаками (зарядом, массой и пр.), тождественными для всех частиц одного сорта.

Подобной атомистичности не существует в макромире. Макроскопические объекты представляют собой совокупности большого числа элементарных частиц. Закономерности макроскопических явлений – это закономерности, свойственные совокупности большого числа частиц.

Все это показывает, что было бы методологически неправильно рассматривать микрочастицы по образу и подобию макроскопических тел. Даже материальная точка классической механики есть абстрактный, идеализированный образ вовсе не микрочастицы, а макроскопического тела, размеры которого малы в сравнении с расстояниями, встречающимися в задаче.

Атомизм микромира не ограничивается определенностью признаков самих микрочастиц. Он выражается также в существовании некоторой абсолютной меры для механического движения. Такой мерой является постоянная Планка . Она имеет первостепенное значение в механике микрочастиц. Физики долгое время стремились понять атомные явления, оставаясь в рамках классических, макроскопических теорий. Открытие постоянной Планком было первым серьезным предупреждением о несостоятельности механического переноса закономерностей из области большого в область малого.

В 20-х годах ХХ столетия были открыты новые опытные факты, заставившие окончательно отказаться от этого пути. Было показано, что электроны обнаруживают волновые свойства: если пропускать поток электронов через кристалл, то частицы распределяются на экране так же, как распределяется интенсивность волн подходящей длины волны. Мы получаем чуждое классической механике явление дифракции микрочастиц. Позднее было доказано, что это явление свойственно не только электронам, но и вообще всем микрочастицам. Таким образом, была открыта принципиально новая и совершенно общая закономерность.

Движение микрочастиц оказалось во многих отношениях более родственно движению волн, нежели движению материальной точки по траектории. Явление дифракции несовместимо с предположением о движении частиц по траекториям. Поэтому принципы классической механики, в которых понятие траектории является одним из основных понятий, непригодны для анализа движения микрочастиц.

Обзор литературы

Литература по квантовой механике на русском языке в настоящее время представлена довольно полно как книгами советских физиков, так и переводами всех основных сочинений иностранных теоретиков. В этих книгах всякий физик, изучающий квантовую механику, или уже применяющий ее в своей практической работе, найдет исчерпывающее изложение основных принципов квантовой механики и многих ее применений, причем уже имеется возможность выбрать книгу сообразно требованиям и склонностям читателя. Квантовая механика вошла настолько глубоко в обиход современного физика, что ему, как правило, постоянно приходится сталкиваться с квантовомеханическим расчетом, с практическим приложением теории к конкретным вопросам. Эти квантовые расчеты содержатся почти во всех книгах, но приводятся они главным образом для иллюстрации общих соображений и не всегда достаточно подробно. В этом отношении книги «» и «», освещая принципиальные вопросы, отличаются наиболее подробным изложением решений основных задач.

В данной курсовой работе приведение подробных расчетов неприменимо в связи с ограничениями по объему. Поэтому можно воспользоваться литературными источниками, в которых основные принципы квантовой механики предполагаются известными и практически не обсуждаются (см. список литературы).

1. Постановка задачи рассеяния. Амплитуда рассеяния

Рассматриваем решение стационарного УШ

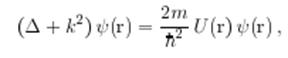                           (1.1)

которое на больших расстояниях r >> a (a — характерный радиус действия потенциала U(r)) имеет вид суперпозиции падающей плоской волны и сферической волны, расходящейся от центра (рис. 1):

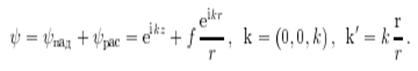          (1.2)

Здесь функция f = f(k,θ,ϕ) — амплитуда рассеяния.

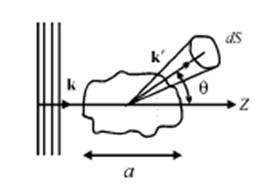
Рис. 1: Схема рассеяния

Дифференциальное сечение рассеяния dσ равно отношению числа частиц, рассеянных в единицу времени в элемент телесного угла dΩ

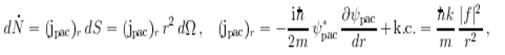
к плотности потока падающих частиц

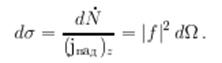
Заметим, что, обсуждая сечение, мы имеем в виду расстояниях r, большие не только по сравнению с a, радиусом действия потенциала, но и с дебройлевской длиной волны λ.

От дифференциального УШ (1.1) и граничного условия (1.2) удобно перейти к интегральному уравнению

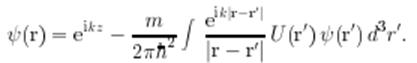         (1.3)

Такой переход можно обосновать известными из электродинамики результатами (см. Ландау Л.Д., Лифшиц Е.М. Теория поля (М.: Наука, 1988, § 64). Действительно, волновое уравнение

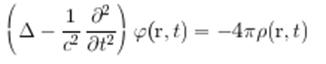
при гармонической зависимости от времени потенциалов и плотностей зарядов

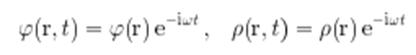
имеет вид

                           (1.4)

аналогичный (1.1) с заменой

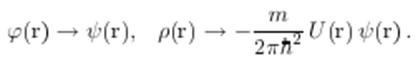
Решение же уравнения (20.4) в форме запаздывающих потенциалов таково:

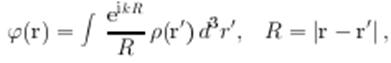
что соответствует суперпозиции сферических волн , расходящихся из центров , в которых сосредоточены заряды .

При r >> a соотношение (1.3) приводится к виду (1.2). Действительно, при этом

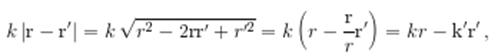
так что

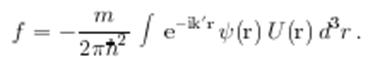           (1.5)

2. Борновское приближение. Формула Резерфорда. Атомный форм-фактор

2.1 Борновское приближение

Рассматриваем потенциал как возмущение. Для получения амплитуды рассеяния в первом порядке по потенциалу взаимодействия, подставим в (1.5) невозмущенную волновую функцию

и получим

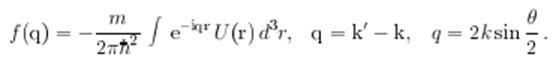
2.2 Критерий применимости

 , что дает для сферически симметричного потенциала условие

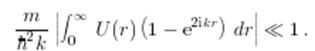
Оно приводится к

Иными словами, характерная потенциальная энергия |U(a)| должна быть мала либо (для медленных частиц) по сравнению с характерной энергией  либо (для быстрых частиц) по сравнению с  (в последнем случае |U(a)| может быть и не мала по сравнению с ).

Критерий применимости борновского приближения для рассеяния медленных частиц  соответствует тому, что в случае притягивающего потенциала притяжение недостаточно для образования связанного состояния. В случае быстрых частиц условие  соответствует тому, что неопределенность в энергии, связанная с временем пролета, должна быть много больше потенциала взаимодействия; условие ka >> 1 обеспечивает здесь применимость квазиклассического рассмотрения.

2.3 Формула Резерфорда

Для поля U(r) = −α/r критерий применимости борновского приближения  Борновская амплитуда равна

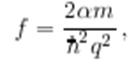
а сечение рассеяния

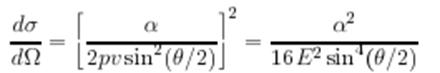
совпадает с классическим. Отметим без доказательства, что борновская формула для сечения совпадает с точной (это верно лишь в нерелятивистском приближении). Полное сечение равно бесконечности.

2.4 Атомный форм-фактор

При упругом рассеянии быстрых электронов на атоме последний можно рассматривать как источник статического потенциала ϕ(r), создаваемого средним распределением зарядов в атоме

Так как  то из

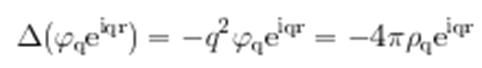
следует, что. Таким образом,

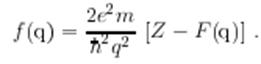
Здесь введен так называемый атомный форм-фактор:

При qa >> 1, то есть при углах рассеяния θ >> 1/ka, форм-фактор |F|<<|Z | и сечение совпадает с резерфордовским. Это вполне естественно: большие углы рассеяния соответствуют малым прицельным параметрам, при которых налетающая частица рассеивается ядром, практически неэкранированным.

При qa << 1 имеем

В этой области дифференциальное сечение

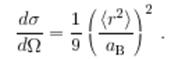
Таким образом, при рассеянии на атоме полное сечение оказывается (в отличие от резерфордовского) конечным.

Пример

Атом водорода. ,поэтому

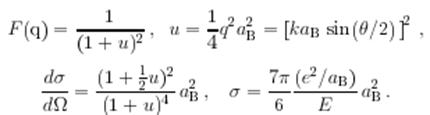
Указанному распределению зарядов соответствует потенциальная энергия

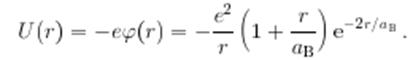
В классической механике в таком поле σ = ∞, что находится в резком противоречии с квантовым (правильным!) результатом.

2.5 Конечные сечения в квантовой механике

Обсудим подробнее вопрос о том, какие потенциалы приводят в квантовой механике к конечным сечениям. Пусть на больших расстояниях . В классической механике при рассеянии в таком поле полное сечение бесконечно, так как любым большим прицельным параметрам ρ соответствуют хотя и малые, но конечные классические углы отклонения

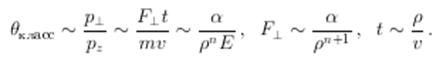
В квантовой механике для частицы с прицельным параметром ρ (у нее  неопределенность поперечного импульса поэтому квантовая неопределенность угла отклонения равна

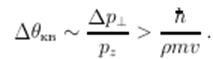
Таким образом, при и поэтому квантомеханические результаты могут существенно отличаться от классических.

Зная поведение U(r) на больших расстояниях, где взаимодействие всегда слабое и поэтому борновское приближение применимо, можно оценить поведение амплитуды в области малых углов рассеяния:

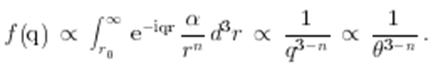
Отсюда получаем, что дифференциальное сечение

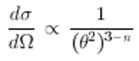
конечно при θ → 0,если n>3, а полное сечение

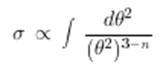
конечно при n>2.

Опыты по рассеянию быстрых электронов на ядрах. Формфакторы элементарных частиц.

3. Фазовая теория рассеяния

Рассеяние на сферически симметричном потенциале является симметричным, то есть ψ(r) зависит лишь от r и θ,но не от ϕ. Поэтому разложение этого решения по парциальным волнам содержит лишь

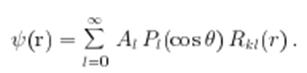                       (3.1)

Как известно (центральное поле сил),

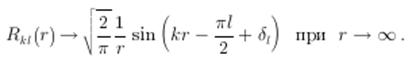
Чтобы выполнялось граничное условие (1.2), необходимо

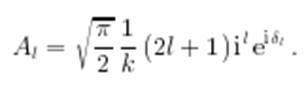
Тогда

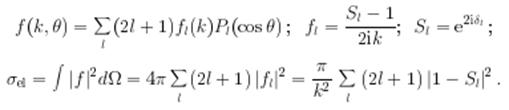
3.1 Понятие о неупругом сечении

Решение (3.1) при r →∞ можно представить не только в виде (1.2), но и в виде двух сферических волн, расходящейся и сходящейся:

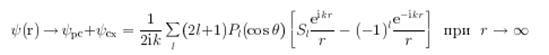
(разумеется, при таком разбиении расходящаяся волнаотличается от в (1.2)). Парциальная амплитуда расходящейся волны отличается на множитель от соответствующей амплитуды в сходящейся волне. Если нет поглощения частиц силовым центром, то этот множитель должен быть по модулю равен единице, .

Если есть поглощение, то , а величина характеризует уменьшение потока частиц в расходящейся волне по сравнению с потоком частиц в сходящейся. Действительно,

Поэтому неупругое сечение равно

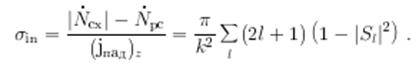
3.2 Оптическая теорема

Для процессов рассеяния и поглощения существуют определенные ограничения и связи. Введем понятие парционального сечения , представив . В классической механике момент импульса , поэтому , а под парциальным сечением естественно понимать площадь кольца между окружностями радиусов и ,то есть

Парциальные сечения для упругого, неупругого и полного  сечения можно записать в виде

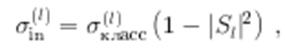
При нет ни поглощения, ни рассеяния; при есть только рассеяние, но нет поглощения. Так как , то

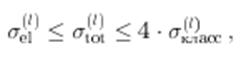
Если есть поглощение частиц  , то непременно происходит и рассеяние частиц. Поглощение максимально при и в этом случае

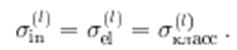
Еще одно соотношение возникает, если сравнить

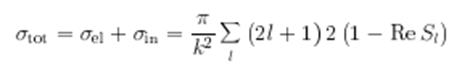
с выражением для мнимой частицы амплитуды рассеяния на угол

нуль:

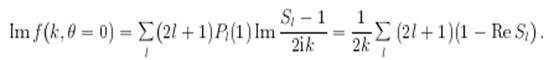
Отсюда получаем оптическую теорему:

Ее смысл тот же, что и в оптике: ослабление падающего потока происходит за счет интерференции падающей волны и волны, рассеянной под очень малыми углами.

3.3 Упругое рассеяние медленных частиц

При ka << 1 прицельные параметры  для , поэтому лишь s-волна может давать заметное рассеяние. Таким образом,

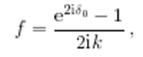
дифференциальное сечение изотропно

а полное сечение определяется фазой s-волны

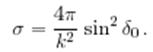
3.4 Дифракционное рассеяние быстрых частиц на черном шаре

Пусть идеально поглощающий (черный) шар имеет радиус a. Рассмотрим рассеяние быстрых (ka >> 1) частиц на таком шаре (пример: нейтроны с энергией E ∼ 100 МэВ рассеиваются на тяжелом ядре радиуса см, при этом ka ∼ 10). Эта задача вполне аналогична дифракции плоской световой волны на черном шаре. Прицельный параметр соответствует .

При частицы не сталкиваются с шаром,  .

При  частицы полностью поглощаются, . Строго говоря, эти утверждения справедливы лишь для , но область  не дает большого вклада в сечение. Таким образом,

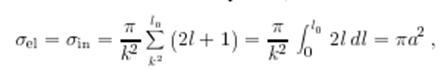
то есть полное сечение вдвое больше классического

Амплитуда упругого рассеяния велика лишь в области малых углов

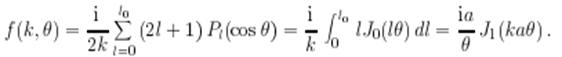
Поэтому

3.5 Упругое рассеяние быстрых частиц на идеально отражающем шаре

Пусть радиус шара a и ka >> 1. Полное сечение определяет число частиц, выбывших из начального пучка. В классике это сечение  связано лишь с прямым столкновением с мишенью. С учетом волновых свойств частиц их выбывание из пучка, то есть изменение начального импульса, связано также с дифракцией.

Как и в предыдущем случае

При  решение УШ для радиальной волновой функции имеет вид  при r < a и

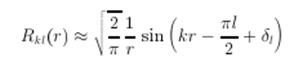
Сшивка при r = a дает . Для нахождения полного сечения используем оптическую теорему

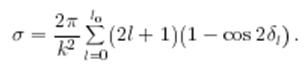
Слагаемые, содержащие , быстро осциллируют при изменении , и поэтому их вкладом в сумму можно пренебречь. В итоге получаем , что вдвое превышает классическое сечение В данном случае отличие от классического результата связано с наличием помимо квазиклассического рассеяния, обусловленного углами θ >> 1/ka, дифракционного рассеяния на малые углы

Чтобы увидеть это, представим амплитуду рассеяния

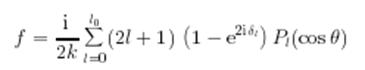
в виде двух слагаемых совпадает с амплитудой рассеяния в предыдущем случае, а

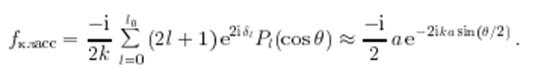
Доказательство того факта, что  (в полном соответствии с классическим изотропным рассеянием ) можно найти в задаче

Таким образом, вклады в полное сечение одинаковы, а вклад их интерференции пренебрежимо мал.

Для классических частиц дифракция практически ненаблюдаема. Так, для частицы с m ∼ 1 г, v ∼ 1 см/с углы дифракции на шаре радиуса a ∼ 1 см настолько малы, , что увидеть это рассеяние можно было бы лишь на расстояниях  см.

3.6 Резонансное рассеяние

Перепишем асимптотическое выражение (при r →∞)

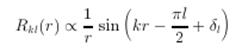
в виде

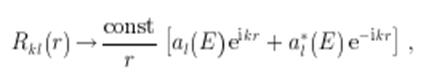
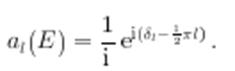
Если в данном поле U(r) возможно квазистационарное состояние при , то асимптотика  при данной энергии должна содержать только расходящуюся волну, то есть

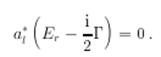
Отсюда следует, что парциальная амплитуда рассеяния

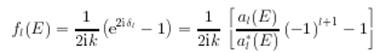
должна иметь полюс при . Пусть вблизи резонанса

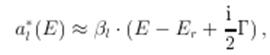
тогда

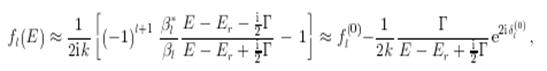
где — фаза и амплитуда рассеяния вдали от резонанса, причем

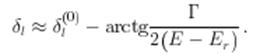
При прохождении через резонанс фаза рассеяния изменяется на π.

Парциальное сечение имеет резонансную зависимость от энергии:

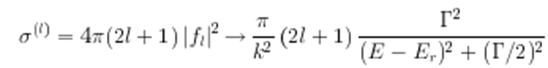
и при достигает максимально возможного значения

При , радиальная волновая функция на больших расстояниях равна

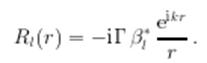
Если  нормирована во внутренней области на единицу, то полный поток в расходящейся волне должен равняться вероятности распада в единицу времени . Отсюда

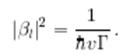
Аналогичным образом можно показать, что при аналитическом продолжении по k функций  в область отрицательных значений E (при этом k → iκ), связанным состоянием с энергией En < 0 соответствуют полюса амплитуды рассеяния при E = En.

Список использованных источников

1. Бете Г. Квантовая механика простейших систем. – М.: ОНТИ, 1935.

2. Блохинцев Д.И. Основы квантовой механики. – М.: Высшая школа, 1976.

3. Галицкий В.М., Карнаков Б.М., Коган В.И. Задачи по квантовой механике. – М.: Наука, 1981.

4. Левич В.Г., Вдович Ю.А., Мямлин В.А. Курс теоретической физики т.2. Квантовая механика, статистика и физическая кинетика. – М.: Наука, 1971.