Электростатика проводников

Предмет макроскопической электродинамики составляет изучение электромагнитных полей в пространстве, заполненном веществом. Как и всякая макроскопическая теория, электродинамика оперирует физическими величинами, усредненными по «физически бесконечно малым» элементам объема, не интересуясь микроскопическими колебаниями этих величин, связанными с молекулярным строением вещества. Так. Вместо истинного «микроскопического» значения напряженности электрического поля е рассматривается ее усредненное значение, обозначаемое .

Основные уравнения электродинамики сплошных сред получаются посредством усреднения уравнений электромагнитного поля в пустоте. Такой переход от микро- к макроскопическим уравнениям был впервые произведен Лоренцем (H.A. Lorentz, 1902).

Вид уравнений макроскопической электродинамики и смысл входящих в них величин существенно зависят от физической природы материальной среды, а также от характера изменения поля со временем. Поэтому представляется рациональным производить вывод и исследование этих уравнений для каждой категории физических объектов отдельно.

1. Электростатическое поле проводников

Как известно, в отношении электрических свойств все тела делятся на две категории - проводники и диэлектрики, причем первые отличаются от вторых тем, что всякое электрическое поле вызывает в них движение зарядов - электрический ток.

Начнем с изучения постоянных электрических полей, создаваемых заряженными проводниками (электростатика проводников). Из основного свойства проводников, прежде всего, следует, что в электростатическом случае напряженность электрического поля внутри них должна быть равной нулю. Действительно, отличная от пули напряженность E привела бы к возникновению тока; между тем распространение тока в проводнике связано с диссипацией энергии и потому не может само по себе (без внешних источников энергии) поддерживаться в стационарном состоянии.

Отсюда в свою очередь следует, что все заряды в проводнике должны быть распределены по его поверхности: наличие зарядов в объеме проводника непременно привело бы к возникновению электрического поля в нем.

Задача электростатики проводников сводится к определению электрического поля в пустоте, вне проводников, и к определению распределения зарядов по поверхности проводников.

В точках, не слишком близких к поверхности тела, среднее поле E в пустоте фактически совпадает с истинным полем e. Эти две величины отличаются друг от друга лишь в непосредственной близости к телу. Точные микроскопические уравнения Максвелла в пустоте гласят:

, ,

(h - микроскопическая напряженность магнитного поля). Так как среднее магнитное поле предполагается отсутствующим, то и производная обращается в результате усреднения в нуль

, ,

т. е. является потенциальным полем с потенциалом , связанным с напряженностью соотношением

и удовлетворяющим уравнению Лапласа

Граничные условия для поля Е на поверхности проводника следуют из самого уравнения . Выберем ось z по направлению нормали n к поверхности проводника в некоторой его точке. Компонента E_z поля в непосредственной близости к поверхности тела достигает очень больших значений.

Существенно, что если поверхность однородна, производные , вдоль поверхности остаются конечными, несмотря на обращение самого E_z в бесконечность. Поэтому из

следует, что конечно. Это значит, что E_y непрерывно на поверхности. То же самое относится и к E_x, а поскольку внутри проводника вообще Е = 0, то мы приходим к выводу, что касательные компоненты внешнего поля на его поверхности должны обращаться в нуль:

E_t = 0.

Таким образом, электростатическое поле должно быть нормальным к поверхности проводника в каждой ее точке. Поскольку , то это значит, что потенциал поля должен быть постоянным вдоль всей поверхности проводника.

Нормальная к поверхности компонента поля просто связана с плотностью распределенного по поверхности заряда. Эта связь получается из общего электродинамического уравнения , которое после усреднения принимает вид

где - средняя плотность заряда. В интегральном виде это уравнение означает, что поток электрического поля через замкнутую поверхность равен полному заряду, находящемуся в ограниченном этой поверхностью объеме. На внутренней площадке Е = 0, найдем, что , где - поверхностная плотность заряда, т. е. заряд на единице площади поверхности проводника. Таким образом, распределение зарядов по поверхности проводника дается формулой

Полный заряд проводника

где интеграл берется по всей его поверхности.

2. Энергия электростатического поля проводников

Вычислим полную энергию U электростатического поля заряженных проводников:

где интеграл берется по всему объему пространства вне проводников. Преобразуем этот интеграл и получим выражение:

аналогичное выражению для энергии системы точечных зарядов.

Заряды и потенциалы проводников не могут быть заданы одновременно произвольным образом; между ними существует определенная связь. Она должна быть линейной, т.е. выражаться соотношениями вида

где величины C_aa, C_abимеют размерность длины и зависят от формы и взаимного расположения проводников. Величины C_aa называют коэффициентами емкости, а величины C_ab- коэффициентами электростатической индукции.

Обратные выражения для потенциалов через заряды:

где коэффициенты составляет матрицу, обратную матрице коэффициентов .

Вычислим изменение энергии системы проводников при бесконечно малом изменении их зарядов или потенциалов:

Это выражение можно преобразовать далее двумя эквивалентными способами. Окончательно имеем:

т.е. получаем изменение энергии, выраженное через изменение зарядов.

С другой стороны:

т. е. изменение энергии выражено через изменение потенциалов проводников.

Эти формулы показывают, что, дифференцируя энергию U по величинам зарядов, мы получаем потенциалы проводников, а производные от U по потенциалам дают значения зарядов:

проводник электромагнитный поле выравнивание

С другой стороны, потенциалы и заряды являются линейными функциями друг друга. Имеем:

а изменив порядок дифференцирования. Мы получили бы . Отсюда видно, что

(и, аналогично, ). Энергия U может быть представлена в виде квадратичной формы потенциалов или зарядов:

Это квадратичная форма должна быть существенно положительной. Из этого условия возникают определенные неравенства, которым удовлетворяют коэффициенты . В частности, все коэффициенты емкости положительны:

(а также и ).

Напротив, все коэффициенты электростатической индукции отрицательны:

3. Проводящий эллипсоид

Задача об определении заряженного проводящего эллипсоида решается с помощью эллипсоидальных координат.

Связь эллипсоидальных координат с декартовыми дается уравнением

Это уравнение, кубическое относительно u, имеет три вещественных корня :

Эти три корня и являются эллипсоидальными координатами точки x, y, z. Их геометрический смысл явствует из того, что поверхности постоянных значений представляют собой соответственно эллипсоиды, однополостные гиперболоиды и двухполюсные гиперболоиды, причем все они софокусны с эллипсоидом

Формулы преобразования от эллипсоидальных координат к декартовым получаются путем совместного решения трех уравнений и имеют вид

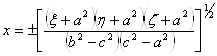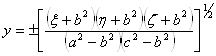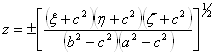Элемент длины в эллипсоидальных координатах имеет вид

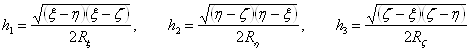где

Соответственно, уравнение Лапласа в этих координатах есть

Тогда кубическое уравнение

вырождается в квадратное

с двумя корнями, пробегающими значения в интервалах

Координатные поверхности постоянных и превращаются соответственно в софокусные сплюснутые эллипсоиды вращения и однополостные гиперболоиды вращения (рис. 1). В качестве третьей координаты можно ввести полярный угол в плоскости

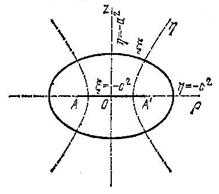
Описание: рис1

Рис. 1

Связь координат с координатами дается равенствами

, .

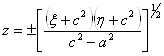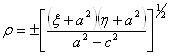Координаты называются сплюснутыми сфероидальными координатами.

При a>b=с эллипсоидальные координаты вырождаются в так называемые вытянутые сфероидальные координаты. Две координаты и задаются корнями уравнения

причем . Поверхности постоянных и представляют собой вытянутые эллипсоиды и двуполостные гиперболоиды вращения (рис. 2).

Связь координат , с координатами дается формулами

, .

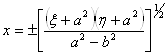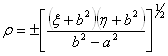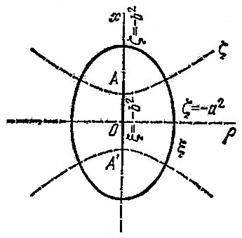
Описание: рис2

Рис. 2

Поверхность

в эллипсоидальных координатах – это координатная поверхность =0. Если искать потенциал поля в виде функции только от , то будут эквипотенциальными все эллипсоидальные поверхности =const, в том числе поверхность проводника. Уравнение Лапласа сводится тогда к уравнению

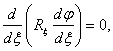
откуда

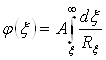Зная, что 2А=е, заключаем:

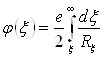Откуда

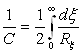Распределение плотности заряда по поверхности эллипсоида определяется нормальной производной потенциала

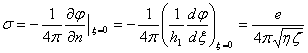Легко убедиться в том, что при =0

Поэтому

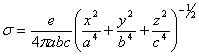Для двухосного эллипсоида интегралы

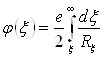выражаются через элементарные функции. Для вытянутого эллипсоида (a>b=c) потенциал поля дается формулой

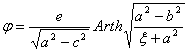а его емкость

Для сплюснутого же эллипсоида (a=b>c) имеем

В частности, для круглого диска (a=b, с=0)

4. Силы, действующие на проводник

В электрическом поле на поверхность проводника действуют со стороны поля определенные силы.

Плотность потока импульса в электрическом поле в пустоте определяется известным максвелловским тензором напряжений:

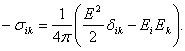
Силе же, действующая на элемент df поверхности теле, есть поток «втекающего» в него извне импульса, т.е. равна . Учитывая, что у поверхности металла напряженность Е имеет только нормальную составляющую, получим

или, вводя поверхностную плотность зарядов ,

Таким образом, на поверхность проводника действуют силы «отрицательного давления».

Полная сила F, действующая на проводник. Получается интегрированием силы по всей его поверхности:

Сила, действующая на проводник вдоль координатной оси q, есть , где под производной надо понимать изменение энергии при параллельном смещении данного тела как целого вдоль оси q. При этом энергия должна быть выражена через заряды проводников (источников поля), и дифференцирование производится при постоянных зарядах. Отмечая это обстоятельство индексом е, напишем

Для системы проводников, потенциалы которых поддерживаются постоянными. Роль механической энергии играет не U, а величина

Подставив сюда

находим, что и отличаются только знаком

Сила получается дифференцированием по q при постоянных потенциалах, т.е.

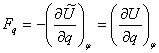Таким образом. Действующие на проводник силы можно получить дифференцированием U как при постоянных зарядах, так и при постоянных дифференциалах.

Выводы

В данной работе рассмотрен предмет электростатики проводников. Проанализированы электростатическое поле проводников, энергия электростатического поля проводников, проводящий эллипсоид, силы, действующие на проводник в поле.