Основные понятия статистики
ТЕМА 1.4. Законы распределения случайных величин, наиболее часто используемые в экономических приложениях, и их числовые характеристики
1. Основные распределения дискретных случайных величин: биномиальное распределение, распределение Пуассона.
2. Основные распределения непрерывных случайных величин: равномерное распределение, показательное распределение, нормальное распределение.
3. Критериальные случайные величины. Распределение Стьюдента, Пирсона, Фишера - Снедекора.
1. Основные распределения дискретных случайных величин: биномиальное распределение, распределение Пуассона.
1.1 Биноминальное распределение
Дискретная случайная величина Х имеет биноминальный закон распределение, если она принимает значения 0, 1, 2, …m… n с вероятностями
![]() ,
,
0< p <1, q = 1 – p, m = 0, 1, 2, …n
Как видно, вероятность значений находится по формуле Бернулли. Следовательно, биноминальный закон распределения представляет собой распределение числа Х = m, количества событий А, произошедших в n испытаниях. Бернулли, в каждом из которых событие A происходит с вероятностью p, а противоположное событие ![]() с вероятностью 1- p.. Закон распределения биноминальной случайной величины Х в развёрнутом форме имеет вид:
с вероятностью 1- p.. Закон распределения биноминальной случайной величины Х в развёрнутом форме имеет вид:
![]()
- верхняя строчка - это совокупность числовых значений, которые может принимать случайная величина;
- нижняя строчка - вероятность события, что случайная величина примет эти значения.
Определение биноминального закона корректно, так как основное свойство ряда распределения ![]() выполнено, ибо
выполнено, ибо ![]() , как было отмечено выше, есть сумма всех членов разложения бинома Ньютона:
, как было отмечено выше, есть сумма всех членов разложения бинома Ньютона:
![]()
Отсюда и название закона – биноминальный.
Числовые характеристики биноминального распределения:
1. М(Х) = np
2. D(X) = npq
1.2 Закон распределения Пуассона
Дискретная случайная величина Х имеет закон распределение Пуассона, если она принимает значения 0, 1, 2, …m,… (бесконечное, но счётное множество значений) с вероятностями
![]() ,
,
где m = 0, 1, 2, …
Числовые характеристики распределения Пуассона:
3. М(Х) = λ
4. D(X) = λ
2. Основные распределения непрерывных случайных величин
Отметим ряд особенностей свойств непрерывных случайных величин.
1. Множество значений непрерывной случайной величины есть совокупность всех точек числовой оси.
2. Функция распределения непрерывной случайной величины.![]() является непрерывной.
является непрерывной.
3. Найдем вероятность того, что в результате испытаний случайная величина X примет значение a, где a - произвольное действительное число:
![]()
В случае непрерывной случайной величины мы сталкиваемся с ситуацией, когда событие принципиально может произойти в результате испытания, но имеет вероятность равную 0. Это надо трактовать так, что распределения непрерывных случайных величин дают нам значения вероятности р = f(x) не для данного значения х случайной величины, а для интервала значений Δ х , примыкающего к х. Поэтому возможно такое определение
Определение. Случайная величина X называется непрерывной, если ее пространством элементарных событий является вся числовая ось (либо отрезок (отрезки) числовой оси), а вероятность наступления любого элементарного события равна нулю.
Естественны следствия такого определения.
1.F(b)-F(a) = P(a£ X< b) = P(a£ X £b)
2.Неотрицательная числовая функция f(x) действительного аргумента x называется плотностью вероятности, и существует в точке x, если в этой точке существует предел:
![]()
Свойства плотности вероятности.
а). 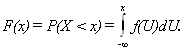
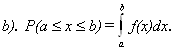

d).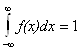
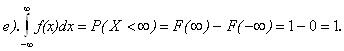
Следствие: Если пространством элементарных событий является отрезок числовой оси, то пространство элементарных событий формально можно распространить на всю числовую ось, положив вне отрезка значение плотности вероятности равное 0.
Примеры непрерывных распределений.
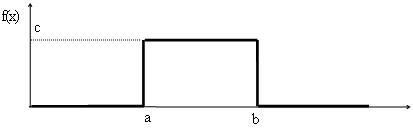
2.1 Равномерное распределение
![]()
х
Найдём константу с :
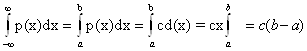
т.к.  .
.
Функция распределения равномерного распределения:
![]()
Математическое ожидание: М(Х) =(а+в)/2, дисперсия D(X) = (b - a)2 /12

x
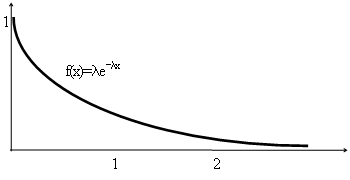
2.2 Показательный закон распределения
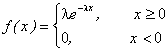
f(x)
x
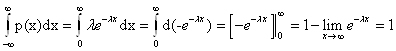
Функция распределения показательного распределения:
![]()
Математическое ожидание: М(Х) = 1/ λ, дисперсия D(X) =1/ λ2
2.3 Нормальное распределение – распределение Гаусса
Случайная величина имеет нормальное распределение (распределение Гаусса) и называется нормально распределенной, если ее плотность вероятности

По определению функция распределения:

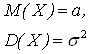
Определение функция плотности распределения корректно, т.к. основное свойство распределения 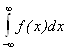 = 1 выполнено, поскольку интеграл
= 1 выполнено, поскольку интеграл

|