Кинетика химических и электрохимических процессов
Министерство образования и науки Российской Федерации
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Федеральное государственное образовательное учреждение высшего профессионального образования
«Чувашский государственный университет им. И.Н. Ульянова»
Методические указания к практическим занятиям по физической химии:
КИНЕТИКА ХИМИЧЕСКИХ И ЭЛЕКТРОХИМИЧЕСКИХ ПРОЦЕССОВ
Чебоксары 2007
УДК 541.1:541.2:541.6
Составители:
С.М. Верхунов
Р.А. Зимин
Э.В. Андреева
Н.И. Кольцов
Кинетика химических и электрохимических процессов: Метод. указания к практическим занятиям по физической химии / Сост. С.М. Верхунов, Р.А. Зимин, Э.В. Андреева, Н.И. Кольцов; Чуваш. ун-т. Чебоксары, 2007. 61 с.
Содержат задачи по следующим темам: электрическая проводимость, равновесия в растворах электролитов, электродвижущие силы, электродные потенциалы, формальная кинетика, сложные реакции, зависимость скорости реакции от температуры, фотохимические реакции. К каждой теме приведены необходимые теоретические сведения, основные уравнения, методики решения задач, предложены задачи для самостоятельного решения с ответами.
Для студентов III и IV курсов химико-фармацевтического факультета.
Ответственный редактор д-р хим. наук, профессор Н.И. Кольцов
Утверждено Методическим советом университета.
1. Электрическая проводимость. Равновесие в растворах электролитов
1.1 Необходимые исходные сведения и основные уравнения
Электролитом называется вещество, которое привзаимодействии с водой способно распадаться на ионы и тем самым переносить электрический заряд. По способу переноса электрического заряда все проводники делятся на два рода. К проводникам первого рода относятся проводники с электронной проводимостью (все металлы, углерод, графит, некоторые неметаллы). К проводникам второго рода относятся проводники с ионной проводимостью (растворы кислот, большинства солей и оснований, а также их расплавы).
Важнейшей характеристикой электрической проводимости является электрическое сопротивление проводников:
R = r∙l/,(1.1)
где r - удельное электрическое сопротивление, Ом.м; l – длина проводника первого рода или расстояние между электродами в проводнике второго рода, м; – площадь поперечного сечения проводника первого рода или площадь электродов проводника второго рода, м2.
Величина, обратная сопротивлению, называется электрической проводимостью:
1/r = c,(1.2)
где c - удельная электрическая проводимость, Ом-1.м-1. Удельной электрической проводимостью называется электрическая проводимость электролита, заключенного между электродами площадью 1 м2 и расположенными на расстоянии 1 м друг от друга.
Для растворов электролитов часто пользуются понятием «эквивалентная электрическая проводимость» l:
l = c/с (1.3)
где с – эквивалентная концентрация электролита, моль.м-3. Эквивалентной электрической проводимостью называется электрическая проводимость электролита, заключенного между электродами, находящимися на расстоянии 1 м друг от друга и такой площади, что в пространстве между ними содержится 1 моль электролита.
Зависимость эквивалентной электрической проводимости от концентрации описывается уравнением Кольрауша:
l = l¥ -А![]() ,(1.4)
,(1.4)
где l¥ - эквивалентная электрическая проводимость при бесконечном разбавлении, Ом-1.моль-1.м2; А – постоянная, зависящая от природы электролита.
Так как проводник второго рода при растворении в воде распадается на два типа ионов, то электрический заряд переносится совместно катионами и анионами и справедливо уравнение Кольрауша (закон независимости движения ионов):
l¥ = l++ l-,(1.5)
где l+ и l- - электрические проводимости соответственно катиона и аниона, Ом-1.моль-1.м2. Электрическая проводимость катиона и аниона в большей степени определяется скоростью их движения:
u+ = u+0U/lи v- = v-0U/l,(1.6)
где u+0 и v-0 – абсолютные скорости движения ионов, м2.с-1.В-1; U/l – напряженность электрического поля, В.м-1,
l+ = F.v+0 и l- = F.v-0,(1.7)
где F – число Фарадея (F = 96500 Кл).
Абсолютные скорости движения ионов различны. Так как в проводниках второго рода электрический заряд переносится од-новременно катионами и анионами, то
Q = Q+ + Q-и I = I+ + I- (1.8)
где Q – перенесенный заряд, Кл; Q+ и Q- - заряд, перенесенный катионами и анионами, Кл; I,I-, I+ - общая сила тока и сила тока, определяемая движением анионов и катионов, А.
Количество заряда, перенесенного ионами, зависит от скорости движения (подвижности), заряда и размера ионов, а также от некоторых других факторов. В большинстве случаев доли зарядов, перенесенных разными видами ионов, не совпадают друг с другом. По этой причине вводится понятие о числах переноса ионов (t+ и t-). Числом переноса ионов называется доля заряда, перенесенного данным видом иона:
t+ = Q+/(Q+ + Q-) = I+/(I+ + I-); (1.9)
t- = Q-/(Q+ + Q-) = I-/(I+ + I-). (1.10)
Очевидно, что t+ + t- = 1. Отсюда:
t+ = 1 – t- и t- = 1 – t+. (1.11)
Числа переноса можно выражать через скорости движения и подвижности ионов:
t+ = v+0/(v+0 + v-0) = λ+/(λ+ + λ-) = λ+/λ∞;
t- = v-0/(v+0 + v-0) = λ-/(λ+ + λ-) = λ-/λ∞. (1.12)
Так как в ходе переноса заряда ионы разряжаются на электродах, то концентрации электролита в анодном, катодном и среднем пространствах различны:
t+ = Δск/Δс иt- = Δса/Δс (1.13)
где Dск и Dса– изменение концентрации электролита в катодном и анодном пространствах; Dс – общая убыль концентрации элек-тролита (изменение концентрации в среднем пространстве).
Количественно степень распада электролита на ионы выра-жается через a (степень диссоциации):
a = p/, (1.14)
где p – количество молекул, распавшихся на ионы; – общее количество молекул электролита, введенных в раствор. По значению a различают сильные и слабые электролиты (a > 0,85 и 0,25 > a > 0,85 соответственно).
При диссоциации слабого электролита, распадающегося на одновалентные ионы по схеме: АВ ↔ А+ + В-, константа диссоциации:
Кд = (А+).(В-)/(АВ), (1.15)
где символы в квадратных скобках указывают на концентрации соответствующих веществ. Если степень диссоциации
a = (А+)/с = (В-)/с = λ/λ∞, (1.16)
то Кд = a2.с, или a = ![]() . (1.17)
. (1.17)
Соотношение (1.17) называется законом разведения Оствальда (в простейшей форме). После подстановки (1.16) в (1.17) закон разведения Оствальда примет вид
Кд = λ2. с/((λ∞.(λ∞ - λ)). (1.18)
Зависимость константы диссоциации от температуры описывается уравнением
lg (К![]() /К
/К![]() ) = -ΔНдисс(1/Т2 – 1/Т1)/(2,3.R), (1.19)
) = -ΔНдисс(1/Т2 – 1/Т1)/(2,3.R), (1.19)
где DНдисс– теплота диссоциации, Дж.моль-1.
Работу диссоциации можно определить по уравнению изотермы Вант-Гоффа:
w = -DG0 = RTlnKи w = -DG0 = 2,3RTlgK, (1.20)
где DG0– стандартное изменение энергии Гиббса (изобарно-изотермического потенциала) при диссоциации, кДж.моль-1.
Необходимо учесть, что для сильных электролитов в приведенные выше уравнения вместо концентрации необходимо подставлять активности, которые связаны с концентрациями через коэффициент активности:
а = g.c, (1.21)
где а – активность сильного электролита, моль.м-3; g - коэффициент активности сильного электролита при данной концентрации, с – молярная концентрация сильного электролита, моль.м-3;
Активностью сильного электролита называется активная часть этого вещества в растворе. Коэффициенты активностей для большинства веществ известны и приведены в справочнике (например, в (8)). Активность электролитов чаще всего выражают через моляльность m и средние ионные коэффициенты активности γ±.
Таблица 1 - Соотношения между моляльностью m, средней ионной моляльностью m±, активностью а и средним ионным коэффициентом активности γ± для некоторых электролитов
| Тип валентности электролита | Пример | а = =(m±∙γ±)ν | а±= =ν |
| 1-1, 2-2, 3-3 | KCl (1-1); ZnSO4 (2-2); AlPO4 (3-3) | m2g±2 | mg± |
| 2-1, 1-2 | CaCl2 (2-1); Na2SO4 (1-2) | 4m3g±3 | 3 |
| 3-1, 1-3 | AlCl3 (3-1), Na3PO4 (1-3) | 27m4g±4 | 4 |
| 3-2, 2-3 | Al(SO4)3 (3-2); Fe3(PO4)2 (2-3) | 108m5g±5 | 5 |
Здесь ν – количество ионов, на которые распадается данный электролит. Моляльностью называется число молей вещества (электролита), содержащегося в 1000 г чистого растворителя (для воды – в 1000 мл).
Зависимость средней ионной моляльности от моляльности электролита выражается уравнением
m±= m(n+n+.n-n-)1/n, (1.22)
где n+и n-- соответственно количество катионов и анионов на которые распадается молекула электролита при диссоциации (n = n+ + n-). Средний ионный коэффициент активности можно выразить через ионные коэффициенты активности:
g± = (g+n+.g-n-)1/n, (1.23)
где g+ и g- - соответственно коэффициенты активности катиона и аниона. Средняя ионная активность составит
а± = m±..g±. (1.24)
Общая активность электролита:
а = (а±)n = а+n+.а-n-, (1.25)
где а+ и а- - соответственно активности катионов и анионов:
а+ = g+.m+иa- = g-.m-. (1.26)
Ионные моляльности связаны с моляльностью электролита соотношениями:
m+ = m×n+ иm- = m×n-. (1.27)
Зависимость среднего ионного коэффициента активности от ионной силы раствора (предельное уравнение Дебая и Гюккеля) имеет вид
lgg±= 0,509.z+. z-.![]() . (1.28)
. (1.28)
где z+ и z- - соответственно заряды катиона и аниона; I– ионная сила раствора:
I = 0,5.åmi.zi2. (1.29)
Cмвол i указывает на тип иона. Для 1-1 - валентного элек-тролита уравнение (1.29) имеет вид
lgg± = -0,509.![]() . (1.30)
. (1.30)
Это уравнение применимо для растворов электролитов, в которых I £ 0,001.
1.2 Задачи с решениями
1. Удельная электрическая проводимость 0,135 моль/л раствора пропионовой кислоты С2Н5СООН равна 4,79.10-2 Ом-1.м-1. Рассчитайте эквивалентную электрическую проводимость раствора, константу диссоциации кислоты и рН раствора, если предельные подвижности Н+ и С2Н5СОО- равны 349,8 Ом.см2/моль и 37,2 Ом.см2/моль соответственно.
Решение: l∞ = 349,8 + 37,2 = 387,0 Ом-1.см2/моль; l = = c.1000/с = 4,79.10-2 Ом-1.м-1/0,135 моль.л-1 = 3,55. a = l/l∞ = = 3,55/387,0 = 0,009. Кд = (a2.с)/(1-a) = (0,0092.0,135)/(1–0,009) = = 1,15.105, (Н+) = a.с = 1,24.10-3 моль/л. рН = – lg (Н+) = 2,91.
Ответ: l = 3,55 Ом-1.см2/моль; a = 0,009; Кд =1,15.10-5 моль/л; рН = 2,91.
2.Для раствора КС1 концентрации 0,01 моль/л удельное сопротивление r = 709,22 Ом.см. Вычислите удельную (c) и эквивалентную (l ) электрические проводимости.
Решение. Удельную электрическую проводимость вычисляем по уравнению (1.2): c = 1/709,22 = 1,41.10-3 = = 0,141. Эквивалентная электрическая проводимость согласно уравнению (1.3) выражается уравнением l = 0,141/0,0 = 0,0141; l = 0,141.10-1.
Ответ: c = 0,141 Ом-1.м-1; l = 1,41.10-2 Ом-1.моль-1.м2.
3.Вычислите эквивалентную электрическую проводимость уксусной кислоты при бесконечном разведении, при 298 К, если электрические проводимости НС1, NаСООСН3, NaCl равны 0,0426; 0,0091; 0,0126 Ом-1.моль-1.м2 соответственно.
Решение. Составляем систему уравнений согласно (1.5):
l∞,HCl = l∞,H+ + l∞,Cl- = 0,0426 Ом-1.моль-1.м2 (1), l∞,CH3COOH = = l∞,Na++l∞,CH3COO- = 0,091 Ом-1.моль-1.м2 (2), l∞,NaCl = l∞,Na+ + + l∞,Cl- = 0,0126 Ом-1.моль-1.м2 (3). Согласно соотношению (1.5) складываем уравнения (1) и (2), вычитаем из них уравнение (3) и получаем
l∞,НС1 + l∞,СН3СООNа – l∞,NaС1 = lН+ + lСН3СОО- = l0,СН3СООН = = 0,0426 + 0,0091 – 0,0126 = 0,0391.
Ответ: l = 0,0391 Ом-1.моль-1.м2.
4.Для бесконечно разбавленного раствора NН4С1 при 298,2 К число переноса катиона t+ = 0,491. Вычислите электрическую подвижность и абсолютную скорость движения аниона С1-; l∞,![]() = 0,0150 Ом-1.моль-1.м2.
= 0,0150 Ом-1.моль-1.м2.
Решение. Согласно уравнениям (1.9 и 1.10) l- = = l∞.(1 – t+) = 0,015.(1-0,491) = 0,00763 Ом-1.моль-1.м2. Абсолютную скорость движения v-0 рассчитываем по уравнению (1.7): v-0 = 0,00763 / 9,65.104 = 7,91.10-8.
Ответ: v-0 = 7,91.10-8 м2/(с.В).
5. При электролизе раствора AgNO3на катоде выделилось 0,5831 г серебра, убыль AgNO3 в катодном пространстве составила 2,85.10-3 моль. Определите числа переноса t- иt+ для нитрата серебра.
Решение. Убыль серебра в катодном пространстве Dск и общая убыль AgNO3 в растворе Dс, соответствующая количеству серебра, выделившегося на катоде, должны быть выражены в одних и тех же единицах. Находим число молей серебра, выделившегося на катоде: Dс = D = m/M =0,5831/107,9=5,4.10-3 моль. Подставим в уравнение (1.13) и получим t- =2,85.10-3/5,4.10-3 = = 0,528;t+ = 1 – t-= 0,472.
Ответ:t- = 0,528; t+ = 0,472.
6. Для 0,1 М раствора Cr2(SO4)3 вычислите среднюю ионную моляльность, активность, общую активность электролита и активности ионов SO42- и Cr3+ при 298 К.
Решение. Среднюю ионную моляльность вычисляем по уравнению
m± = m (n+n+n-n-)1/n = (22.33)1/5. 0,1 = 0,255. Среднюю ионную активность вычисляем по уравнению а±= m±. g±.(g±= 0,0458 = = 0,255.0,0458=0,0177. Общую активность электролита а вычисляем по уравнению а = (а±)n = (0,0177)5 = 2,17.1010. Ионные моляльности m![]() и m
и m![]() рассчитаем по уравнениям: m
рассчитаем по уравнениям: m![]() = = m.n
= = m.n![]() = 0,1.3 = 0,3; m
= 0,1.3 = 0,3; m![]() = m.n
= m.n![]() = 0,1.2 = 0,2; активности аниона и катиона определяем по уравнениям а
= 0,1.2 = 0,2; активности аниона и катиона определяем по уравнениям а![]() = g
= g![]() х х m
х х m![]() = 0,3.0,0458 = 0,0137; a
= 0,3.0,0458 = 0,0137; a![]() = g
= g![]() . m
. m![]() = = 0,2.0,0458 = 0,0092.
= = 0,2.0,0458 = 0,0092.
Ответ: m±=0,255 моль/1000 г; g±=0,0177; a=2,17.1010 моль/л; m![]() 0,3 моль/1000г; m
0,3 моль/1000г; m![]() =0,2 моль/1000 г; a
=0,2 моль/1000 г; a![]() = =0,0137 моль/л; a
= =0,0137 моль/л; a![]() =0,0092 моль/л.
=0,0092 моль/л.
7. Определите ионную силу I раствора, содержащего 0,001 моль Н2SO4 и 0,002 моль MgSO4 на 1000 г воды при 298 К.
Решение. Согласно уравнению (1.30): I = 0,5.(m![]() ..z+2 ++m
..z+2 ++m![]() ..z-2- + m
..z-2- + m![]() ..z+2+ m
..z+2+ m![]() ..z-2). Моляльности ионов определяем по уравнению (1.30). Тогда ионная сила I=1/2.(2.0,001.12+0,001.22+0,002.22+0,002.22) = 0,011.
..z-2). Моляльности ионов определяем по уравнению (1.30). Тогда ионная сила I=1/2.(2.0,001.12+0,001.22+0,002.22+0,002.22) = 0,011.
Ответ:I = 0,011.
8. Удельная электрическая проводимость с = 5%-го раствора нитрата магния при 18 оС равна 4,38 Ом-1.м-1, а его плотность – 1,038 г.см-3. Рассчитайте эквивалентную электрическую проводимость раствора λ и кажущуюся степень диссоциации соли в растворе. Подвижности ионов Mg2+ и NO3- при 18 оС равны 44,6 и 62,6 Ом-1.см2.моль-1.
Решение. М = с.r/М![]() = 0,05.1,038/148.1000 = = 0,70 моль.л-1; l = c/(с.1000) = 4,38/(0,70.1000) = = 6,25.10-3; l∞= 44,6 + 62,6 =107,2 Ом-1.см2.моль-1; a = l/l∞ = 62,5/107,2 = 0,583.
= 0,05.1,038/148.1000 = = 0,70 моль.л-1; l = c/(с.1000) = 4,38/(0,70.1000) = = 6,25.10-3; l∞= 44,6 + 62,6 =107,2 Ом-1.см2.моль-1; a = l/l∞ = 62,5/107,2 = 0,583.
Ответ: l = 62,510-3 Ом-1.м2.моль-1; a = 0,583.
1.3 Задачи для самостоятельного решения
1. Константа диссоциации масляной кислоты С3Н7СООН равна 1,5.10-5. Вычислите степень ее диссоциации в 0,005 М растворе.
2. Чему равна концентрация ионов водорода в водном раст-воре муравьиной кислоты, если α = 0,03?
3. Вычислите ионную силу и активность ионов в растворе, содержащем 0,01 моль/л Ca(NO3)2 и 0,01 моль/л CaCl2.
4. Рассчитайте активность электролита а и среднюю ионную активность а± в растворе CaCl2 при 25 оC, если средний ионный коэффициент активности γ± = 0,518, а молярная концентрация m= 0,1.
5. Для реакции диссоциации муравьиной кислоты: НСООН ↔ Н+ + НСОО- дана зависимость константы от температуры: lgКД = -1342,85/Т + 5,2743 – 0,0152.T. Вычислите теплоту диссоциации муравьиной кислоты в разбавленном вод-ном растворе.
6. Определите температуру, при которой диссоциация му-равьиной кислоты в водном растворе максимальна. Уравнение зависимости константы диссоциации НСООН от температуры приведено в предыдущей задаче.
7. Рассчитайте удельную электрическую проводимость абсолютно чистой воды при 25 оС. Ионное произведение воды при этой температуре равно 1.10-14.
8. Эквивалентные электрические проводимости бесконечно разбавленных растворов KCl, KNO3, и AgNO3 при 25 оС равны соответственно 149,9, 145,0 и 133,4 Ом-1.см2.моль-1. Какова эквивалентная электрическая проводимость бесконечно разбавленного раствора AgCl при этой температуре?
9. Удельная электрическая проводимость 4 % -го водного раствора Н2SO4 при 18 оС равна 0,168 Ом-1.см-1, плотность раствора равна 1,026 г/см3. Рассчитайте эквивалентную электри-ческую проводимость этого раствора.
10. Для 0,01 молярного раствора KCl удельное сопротивление равно 709,22 Ом.см. Вычислите удельную и эквивалентную электрические проводимости.
11. Какую долю общего тока переносит ион Li+ в водном растворе LiBr при 25 оС?
12. Эквивалентная электрическая проводимость раствора уксусной кислоты молярной концентрации 1,59.10-4 моль.л-1 при 25 оС равна 12,77 Ом-1.см2.моль-1. Рассчитайте константу диссо-циации кислоты и рН раствора.
13. Для бесконечно разбавленного раствора NH4Cl при 298,2 К число переноса катиона t+ = 0,491. Вычислите электро-литическую подвижность и абсолютную скорость движения аниона Cl-; λ∞(NH4Cl) = 0,015 Ом-1.моль-1.м2.
14. При электролизе раствора AgNO3 на катоде выделилось 0,5831 г серебра, убыль AgNO3 в анодном пространстве соста-вила 2,85.10-3 моль. Определите числа переноса t+иt- для AgNO3.
15. При электролизе раствора AgNO3 c серебряными электродами увеличение количества соли в анодном про-странстве составило 0,0625 г. Чему равна убыль соли, г, в катодном пространстве?
2. ЭЛЕКТРОДВИЖУЩИЕ СИЛЫ. ЭЛЕКТРОДНЫЕ ПОТЕНЦИАЛЫ
2.1 Необходимые исходные сведения и основные уравнения
ЭДС гальванического элемента Е равна разности условных электродных потенциалов его полуэлементов φ1 и φ2. Если значением диффузионного потенциала можно пренебречь то
Е = φ2 - φ1(2.1)
(индекс 2 относится к более положительному электродному потенциалу). Электрохимические реакции, протекающие на электродах, и сами электроды разделяют на следующие типы:
1. Электроды 1-го рода, обратимые по катиону: Меn+ + ne = =Ме0, где Меn+ и Ме0 ― окисленная и восстановленная формы вещества; е - количество электронов. Потенциал электрода 1-го рода рассчитывается по уравнению Нернста:
φ = φ0![]() (aOx/aRed),(2.2)
(aOx/aRed),(2.2)
где φ - потенциал электрода, В; φ0 - стандартный потенциал электрода, В; - число электронов, участвующих в элемен-тарной реакции; F - число Фарадея; aRed и aOx - активности вос-становленной и окисленной форм вещества, вступающего в реакцию. Множитель ![]() при Т = 298 К и значении R, равном 8,31 Дж/(моль.К), равен 0,059. К электродам 1-го рода относятся:
при Т = 298 К и значении R, равном 8,31 Дж/(моль.К), равен 0,059. К электродам 1-го рода относятся:
а) серебряный электрод:
Ag+│Ag; Ag+ + e= Ag0; =1;aOx= aAg+; aRed =aAg =1,
φ = φ0Ag+ ![]() lgaAg+; (2.3)
lgaAg+; (2.3)
б) амальгамный электрод:
Cd2+ │(Cd) (Hg)Cd2+ + 2e = (Cd)ам; = 2; aOx = aCd+
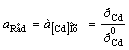 ; φ = φ0AСd2+
; φ = φ0AСd2+ 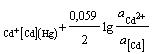 ,(2.4)
,(2.4)
где φ![]() - потенциал амальгамного электрода при активности кадмия в амальгаме, а(Cd) = 1;
- потенциал амальгамного электрода при активности кадмия в амальгаме, а(Cd) = 1;
в) газовый электрод:
H+ │Pt, H2; H+ + e =½ H2; = 1; aOx = aH++; aRed = ![]() =
= ![]() ;
;
φ = φ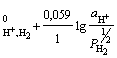 .(2.5)
.(2.5)
2. Электроды 2-го рода, обратимые по аниону, представляют собой металл, покрытый труднорастворимой солью этого метал-ла, который находится в равновесии с раствором, содержащим соответствующий анион: AgCl + e = Ag + Cl-; =1; aOx = aAgCl = 1; aRed = aCl-;
φ = φ![]() ; (2.6)
; (2.6)
φ02 =φ![]() ,(2.7)
,(2.7)
где j ![]() ― стандартный потенциал серебряного электрода, обратимого по катиону; ПРAgCl ― произведение растворимости хлорида серебра. К электродам 2-го рода относятся:
― стандартный потенциал серебряного электрода, обратимого по катиону; ПРAgCl ― произведение растворимости хлорида серебра. К электродам 2-го рода относятся:
а) газовый электрод:
½ Cl2 + e = Cl-; = 1; aOx = ![]() ; aRed =
; aRed = ![]() ;
;
φ = φ![]() . (2.8)
. (2.8)
б) каломельный электрод Cl-│Hg2Cl2, на котором идет электродная реакция HgCl2 + 2e = Hg+ + 2Cl- ;
φ![]() φ
φ![]() .
.
в) хлорсеребряный электрод Cl-│AgCl, Ag, на котором идет электродная реакция AgCl + e = Ag+ + Cl-;
φ![]() φ
φ![]() .
.
Окислительно-восстановительные электроды (редокси – электроды) представляют собой инертный металл, опущенный в раствор, содержащий окисленную и восстановленную формы. Уравнение Нернста для данных электродов имеет вид:
φ Red= φ![]() , (2.9)
, (2.9)
где аОх(аО) ― активность окисленного иона; aRed(aВ) - активность восстановленного иона. Они делятся:
а) на простые: Fe3+ + e = Fe2+; = 1; aRed = ![]() ; aOx =
; aOx = ![]() ;
;
φ = φ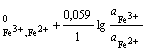 ; (2.10)
; (2.10)
![]() ; = 1;
; = 1; ![]() ;
; ![]() ;
;
φ = φ![]() ;(2.11)
;(2.11)
б) на сложные:
![]() ;
;
φ = φ . (2.12)
. (2.12)
Хингидронный электрод: C6H4O2 (хинон) + 2H+ + 2e = = C6H4(OH)2 (гидрохинон);
n = 2, aRed = aгх = 1; аОх = ах= 1;
φ = φ![]() + φ
+ φ![]() . (2.13)
. (2.13)
Связь константы равновесия химической реакции и стандартных электродных потенциалов выражается соотноше-нием
![]() (φ02 – φ01)./0,0592 (Т = 298 К). (2.14)
(φ02 – φ01)./0,0592 (Т = 298 К). (2.14)
Для концентрационных цепей уравнение Нернста (при отсутствии диффузионного потенциала) для электродов типа
Cu | Cu2+ ║ Cu2+ | Cu ; Ag, AgCl | HCl ║ HCl | Ag, AgCl
a1 a2 (a2 > a1) a1 a2 (a2 > a1)
имеет вид
![]() , (2.15)
, (2.15)
где а1 и а2 ─ активности ионов Cu2+ и Cl- соответственно.
Для электродов 2-го рода типа: Pt, H2 (P1) | HCl | Pt, H2 (P2), уравнение (2.15) преобразуется в уравнение
![]() (Р1/Р2), (2.16)
(Р1/Р2), (2.16)
где P1 и P2 - давления водорода, P1 > P2.
Для амальгамного элемента: Hg (Cd) (a1) | Cd2+ | Hg (Cd) (a2), (a2 > a1), уравнение Нернста имеет вид
![]() (а1/а2), (2.17)
(а1/а2), (2.17)
где a1 иa2 ─ активности металлического кадмия в амальгаме. Для элемента типа: Cd(ж) (a1 = 1) | Cd в расплаве солей | Cd в расплаве Cd – Sn (a2) уравнение (2.17) принимает вид
![]() , (2.18)
, (2.18)
где a2 ─ активность кадмия в расплаве Cd – Sn.
Расчет ЭДС концентрационной цепи (например, серебряной, Ag | AgNO3 (а1) ║ AgNO3 (а2) | Ag,) производится по формуле
Е = 2.0,059. l∞,![]() . lg(а1/а2) /(l∞,
. lg(а1/а2) /(l∞,![]() +l∞,
+l∞,![]() ) (2.19)
) (2.19)
где λ∞,Ag+ и λ∞,![]() - подвижности аниона и катиона.
- подвижности аниона и катиона.
Термодинамические функции ΔG, ΔS, ΔH для электрохимических реакций рассчитывают по уравнениям:
ΔG = - nEF, (2.20)
![]() , (2.21)
, (2.21)
![]() , (2.22)
, (2.22)
![]() , (2.23)
, (2.23)
![]() , (2.24)
, (2.24)
где – число электронов, участвующих в реакции; F – число Фарадея, Кл; E – ЭДС, В.
2.2 Задачи с решениями
электролит проводимость потенциал кинетика
1. Гальванический элемент состоит из металлического цинка, погруженного в 0,1 М раствор нитрата цинка, и металлического свинца, погруженного в 0,02 М раствор нитрата свинца. Вычислите ЭДС элемента.
Решение. Чтобы определить ЭДС элемента, необходимо вычислить электродные потенциалы. Для этого из табл. (8), берем значения стандартных электродных потенциалов систем Zn2+|Zn (-0,76 В) и Pb2+|Pb (-0,13 В), а затем рассчитываем значение φ по уравнению Нернста: φZn/Zn2+ = -0,76+(0,059.lg0,1)/2 = =-0,79 В, φPb/Pb2+=-0,13+(0,059.lg0,02)/2=-0,18 В. Находим ЭДС элемента: Е = φPb/Pb2+ – φZn/Zn 2+ = -0,18+0,79 = 0,61.
Ответ:0,61 В.
2. Вычислите потенциал серебряного электрода в насыщенном растворе AgBr (ПР = 6.10-13), содержащем, кроме того, 0,1 моль/л бромида калия.
Решение. Запишем уравнение Нернста для системы Ag+|Ag: φ= φ0 + 0,059.lg(Ag+). Значение φ0 для этой системы составляет 0,8 В (табл. (8)). Поскольку бромид калия полностью диссоциирован, то (Br-)=0,1 моль/л. Отсюда находим концентрацию ионов серебра: (Ag+) = ПРAgBr/(Br-) = 6.10-13/0,1 = = 6.10-12 моль/л. Теперь подставляем значения φ0 и (Ag+) в уравнение электродного потенциала: φ = 0,8 + 0,059.lg(6∙10-12) = = 0,14.
Ответ: 0,14 В.
3. Вычислите активность ионов Н+ в растворе, в котором потенциал водородного электрода равен 82 мВ.
Решение. Из уравнения φ = -0,059рН находим: рН = = 0,082/0,059 = 1,39. Следовательно, аН+ = 0,041.
Ответ: аН+ = 0,041 моль/л.
4. Рассчитайте стандартный электродный потенциал пары Cu2+|Cu+ по следующим данным: φ0Cu2+|Cu = 0,337 В, φ0Cu+|Cu = = 0,521 В.
Решение. Для реакции Cu2+ + 2е = Cu, ΔG0 = -nFЕ0 = = −2.96485.0,337 = −65031 Дж.моль-1. Для реакции Cu+ + е = Cu, ΔG0 = −96485.0,521 = −50269 Дж.моль-1. Вычитая из первой реакции вторую, получим Cu2+ + е = Cu+ и, следовательно, ΔG0 = = −14762 Дж.моль-1, откуда Е0 = 0,153.
Ответ: Е0 = 0,153 В.
5. ΔН реакции Pb + Hg2Cl2 = PbCl2 + 2Hg, протекающей в гальваническом элементе, равно −94,2 кДж/моль при 298,2 К. ЭДС этого элемента возрастает на 1,45.10-4 В при повышении температуры на 1 К. Рассчитайте ЭДС элемента и ΔS при 298,2 К.
Решение. ![]() = 2,96485.1,45.10-4 = = 28,0. ΔG= ΔН – ТΔS= nFE, откуда E= − (ΔН - ТΔS)/nF= = 0,5314.
= 2,96485.1,45.10-4 = = 28,0. ΔG= ΔН – ТΔS= nFE, откуда E= − (ΔН - ТΔS)/nF= = 0,5314.
Ответ: ΔS = 28,0 Дж/(моль.К); E= 0,5314 В.
6. Рассчитайте константу равновесия реакции Cd2+ + Zn = = Zn2+ + Cd, если φ0Cd2+/Cd= -403 В; φ0Zn2+/Zn= -0,763В.
Р е ш е н и е. Константу равновесия вычисляем по уравнению: ![]() (φ02 – φ01).n/0,0592. После подстановки данных получим
(φ02 – φ01).n/0,0592. После подстановки данных получим ![]() = 12,16. Откуда К = 1,45.1012.
= 12,16. Откуда К = 1,45.1012.
Ответ: К = 1,45.1012.
2.3 Задачи для самостоятельного решения
1. Гальванический элемент состоит из серебряного электрода, погруженного в 2 М раствор AgNO3, и стандартного водородного электрода. Напишите уравнения электродных процессов и суммарной реакции, происходящей при работе элемента. Определите его ЭДС.
2. Рассчитайте электродные потенциалы магния в растворе его соли при концентрациях иона Mg2+, равной 0,1; 0,01 и 0,001 моль/л.
3. Вычислите потенциал свинцового электрода в насыщенном растворе PbBr2, если (Br-) = 1 моль/л, а ПРPbBr2+= 9,1.10-6.
4. Гальванический элемент составлен из стандартного цинкового электрода и хромового электрода, погруженного в раствор, содержащий ионы Cr3+. При какой концентрации ионов Cr3+ ЭДС этого элемента окажется равной 0?
5. ЭДС гальванического элемента, составленного из 2 водородных электродов, равна 272 мВ. Чему равен рН раствора, в который погружен анод, если катод погружен в раствор с рН = 3?
6. Рассчитайте константу равновесия реакции диспропорционирования 2 Cu+ + Cu2+ + Cu при 25 оC.
7. Рассчитайте константу равновесия реакции ZnSO4 + Cd = = CdSO4 + Zn при 25 оС по данным о стандартных электродных потенциалах.
8. Рассчитайте потенциал водородного электрода в чистой воде при 25 оС.
9. ЭДС элемента, в котором обратимо протекает реакция 0,5 Hg2Cl2 + Ag = AgCl + Hg, равна 0,456 В при 298 К и 0,439 В при 293 К. Рассчитайте ΔG, ΔH и ΔS реакции.
10. Значение ΔНреакции Pb + 2 AgCl = PbCl2 + Ag, протекающей в гальваническом элементе, - 105,1 кДж/моль. ЭДС этого элемента равна 0,4901 В при 298,2 К. Рассчитайте ЭДС элемента при 293,2 К.
11. Вычислите полезную работу реакции Ag + 0,5Cl2 = AgCl, используя данные о нормальных электродных потенциалах, если Р![]() = 101,3 кПа, Т = 298 К.
= 101,3 кПа, Т = 298 К.
12. Температурный коэффициент элемента, работающего за счет реакции: Pb + Hg2Cl2 = PbCl2 + 2 Hg, ![]() = 1,45.10-4 В/К. Определите количество теплоты, выделяющейся (поглощающейся) при работе элемента и сопоставьте полученное значение с тепловым эффектом, рассчитанным по следствию из закона Гесса.
= 1,45.10-4 В/К. Определите количество теплоты, выделяющейся (поглощающейся) при работе элемента и сопоставьте полученное значение с тепловым эффектом, рассчитанным по следствию из закона Гесса.
13. Для гальванического элемента, в котором протекает реакция Hg2SO4 + Pb = PbSO4 + 2Hg вычислите ЭДС при 298 К и температурный коэффициент ![]() , используя данные таблиц стандартных термодинамических величин.
, используя данные таблиц стандартных термодинамических величин.
14. Рассчитайте потенциал серебряного электрода, опущенного в насыщенный раствор AgI, по данным о произведении растворимости соли и нормальном электродном потенциале