Теория статистики
Статистика – одна из древнейших отраслей знаний, возникшая на базе хозяйственного учета.
Первые учетные операции проводились еще в глубокой древности. Вначале они были довольно примитивны, нерегулярны и направлены главным образом на получение данных о численности населения, его составе и имущественном положении. Эти данные использовались прежде всего при налогообложении и в военных нуждах.
По мере развития производительных сил в обществе возрастал интерес к различного рода знаниям, расширялся круг учитываемых явлений и собираемых о них сведений; усложнялись сами учетные операции, они стали более регулярными. Постепенно накапливался опыт, появлялись рекомендации о том, каким образом организовать отдельные учетные операции и обработать собранные сведения, чтобы обобщить их и выявить различные закономерности.
Так постепенно сформировалась отрасль знаний, названная впоследствии "статистикой". Ее возникновение связано с потребностями общества в различного рода сведениях, информации, без которых невозможно управлять государством, изучать отдельные явления и процессы, происходящие в различных областях жизни, сферах деятельности.
Есть основания полагать, что термин "статистика" произошло от латинских слов stato (государство) и status (положение вещей, политическое состояние). В середине 18 в. под статистикой подразумевалась совокупность сведений о государстве, о его достопримечательностях. В научный обиход этот термин ввел немецкий ученый Готфрид Ахенваль, представитель описательной школы государствоведения. В 1746 г. он предложил заменить название курса "Государствоведение" на "Статистику", положив тем самым начало развитию статистики как науки и учебной дисциплины.
Статистика изучает, как правило, массовые явления, т.е. такие явления, которые состоят из множества отдельных элементов или фактов.
Однако недостаточно только провести массовое наблюдение, чтобы выявить те или иные закономерности.
Результаты наблюдения подвергают обработке, сводке, что позволяет выделить во всей совокупности различные типы, группы единиц и затем для всей совокупности и отдельных ее частей рассчитать обобщающие показатели (характеристики).
Массовое наблюдение, группировка и сводка его результатов, вычисление и анализ обобщающих показателей – все это вместе составляет специфический метод статистики.
К какой бы области ни относился предмет статистики (население, промышленность, торговля и т.д.), метод ее везде одинаков, т.е. везде используется массовое наблюдение, группировка и обобщающие показатели, в которых, благодаря действию закона больших чисел, взаимопогошается влияние случайных причин и выявляется типичное и закономерное. Иначе говоря, метод статистики обусловлен спецификой ее предмета.
Чтобы пользоваться результатами обобщения или непосредственно исходной информацией, данные должны быть представлены в подходящей форме, компактно и наглядно. С этой целью строятся таблицы и графики
1. Средние величины и показатели вариации
медиана дисперсия индекс себестоимость
В статистике средними величинами называют обобщающие показатели, выражающие типичные, характерные для определенного места и времени размеры и количественные соотношения явлений общественной жизни.
Средние величины бывают следующих видов: арифметическая, геометрическая, гармоническая, квадратическая, кубическая и др.
В зависимости от частоты повторения вариант средние исчисляются как простые не взвешенные, так и взвешенные.
Среднюю арифметическую не взвешенную рассчитывают по формуле:
![]() =
=![]() .
.
При расчете средних величин отдельные значения осредняемого признака могут повторяться, тогда расчет средней производится по сгруппированным рядам (дискретными или интервальными). В таком случае используется для расчета средней величины формула средней арифметической взвешенной:
 ,
,
где xi – значение осредняемого признака,
fi – частота,
– число единиц совокупности.
Средняя гармоническая невзвешенная определяется по формуле:
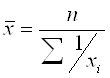 .
.
Если же в условии даны показатели об урожайности культуры и ее валовом сборе, например, то для расчета средней урожайности применяется формула средней гармонической взвешенной:
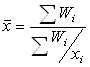 ,
,
где ![]() - сумма значений осредняемого признака по группе;
- сумма значений осредняемого признака по группе;
xi – значение осредняемого признака.
Средняя гармоническая вычисляется в тех случаях, когда средняя предназначенная для расчета сумм слагаемых, обратно пропорциональных величине заданного признака, т.е. когда суммированию подлежат не сами варианты, а обратные им величины.
Аналогичен подход для расчета средней цены, среднего процента выполнения плана, средний производительности труда и т.п.
Средняя геометрическая определяется по формуле:
![]()
Наиболее широкое применение средняя геометрическая получила для определения среднегодовых темпов роста в рядах динамики.
При выборе того или иного вида средней следует исходить из того, что средняя применена правильно тогда, когда она имеет реальный экономический смысл.
Разновидностью средней являются мода и медиана. Эти величины также используются в качестве характеристик вариационного ряда.
Мода (М0) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой.
Для дискретного ряда распределения мода определяется наиболее просто: варианта, против которой располагается наибольшая частота, и будет модой.
В интервальном ряду наибольшая частота указывает не на модальную варианту, а на содержащий моду интервал. Поэтому в модальном интервале необходимо определить модальную варианту. При этом надо иметь в виду, что при расчетах будет получено не точное, а некоторое условное значение моды, так как неизвестен характер распределения частоты внутри модального интервала.
Вычисление моды в интервальном ряду производится по следующей формуле:
 ,
,
где ![]() - начало (нижняя граница) модального интервала;
- начало (нижняя граница) модального интервала;
![]() - величина интервала;
- величина интервала;
![]() - частота модального интервала;
- частота модального интервала;
![]() - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному;
![]() - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.
Медианой (Ме) называется значение признака приходящееся на середину упорядоченной совокупности. Для ее определения достаточно расположить в порядке возрастания или убывания все варианты. Средняя варианта и будет являться медианой. Расчет медианы для интервального ряда производится по формуле:
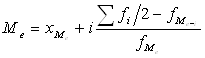 ,
,
где ![]() - начало (нижняя граница) медианного интервала;
- начало (нижняя граница) медианного интервала;
![]() - сумма накопленных частот ряда;
- сумма накопленных частот ряда;
![]() - величина интервала;
- величина интервала;
![]() - накопленная частота варианта, предшествующих медианному;
- накопленная частота варианта, предшествующих медианному;
![]() - частота медианного интервала.
- частота медианного интервала.
Информация о средних уровнях обычно бывает недостаточной для полного анализа изучаемого процесса или явления. Необходимо учитывать и разброс, т.е. вариацию значений отдельных единиц совокупности.
Для характеристики размеров колеблемости признаков в статистике применяется следующие показатели: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратичное отклонение, коэффициент вариации и др.
Размах вариации представляет собой разность между наибольшим и наименьшим значением вариации, т.е.
![]() .
.
Среднее линейное отклонение определяется из отношения суммы, взятой по абсолютной величине (без учета знака) отклонения всех вариант от средней арифметической, к объему всей совокупности. Оно бывает взвешенное и незвешенное и определяется соответственно по формулам:
 ,
,
 .
.
Дисперсия – это средняя из квадратов отклонений значений признака от его средней арифметической величины. Она определяется по формуле арифметической простой:
 .
.
Или средней арифметической взвешенной:
![]() .
.
Если имеются два взаимоисключающих друг друга варианта, от вариации признака называется альтернативной. Обозначая наличие признака – 1, а отсутствие – 0, и долю вариантов обладающих данным признаком – p, а долю вариантов, не обладающих им –q и замечая, что p+q=1, получаем среднюю:
![]() .
.
Дисперсию альтернативного признака определяем по формуле:
 .
.
Следовательно, дисперсия альтернативного признака находится по формуле:
![]() .
.
Среднее квадратичное отклонение - это корень квадратный из дисперсии – определяется по формулам средней арифметической простой:
 .
.
Или средней арифметической взвешенной:
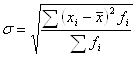 .
.
Среднее квадратическое отклонение альтернативного признака:
![]() .
.
Мерой сравнения степеней колеблемости для двух, трех и более вариационных рядов служит показатель, который носит название коэффициента вариации и определяться по формуле:
![]() %.
%.
Задание 1
По цехам вагоноремонтного завода имеются следующие данные о заработной плате сотрудников
Таблица 1
| Предприятие | Базисный период | Отчетный период | ||
| Средняя заработная плата, руб. | Число рабочих | Средняя заработная плата, руб. | Фонд заработной платы, руб. | |
| I | 3130 | 220 | 3560 | 961200 |
| II | 3340 | 280 | 3870 | 870750 |
| III | 3870 | 310 | 4150 | 1784500 |
| Итого | 810 | 3616450 | ||
Вычислите среднемесячную заработную плату по заводу: а)за базисный период; б) за отчетный период.
Сравните полученные результаты.
Решение
Среднемесячная заработная плата за базисный период:
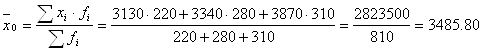 руб.
руб.
Среднемесячная заработная плата за отчетный период:
 руб.
руб.
Вывод: Сравнивая полученные результаты видно, что среднемесячная заработная плата в отчетном периоде по сравнению с базисным возросла на 423.88 руб. и составила 3909.68 руб.
Задание 2
Определите среднюю скорость движения поездов на направлении, показатели ее вариации, моду и медиану. Укажите вид используемой средней.
Таблица 2
| Скорость поезда, км/ч | 130 | 110 | 90 | 80 | 60 | 50 |
| Длина участка, км | 100 | 200 | 150 | 170 | 165 | 110 |
Решение
Определим среднюю (таблица 3):
Таблица 3
Скорость поезда, км/ч xi | 130 | 110 | 90 | 80 | 60 | 50 | Сумма |
Длина участка, км Wi | 100 | 200 | 150 | 170 | 165 | 110 | 895 |
Время, ч | 0,769 | 1,818 | 1,667 | 2,125 | 2,750 | 2,200 | 11,329 |
| 39,23 | 56,36 | 18,33 | 2,12 | 52,25 | 63,80 | 232,102 |
| 2000,75 | 1747,245 | 201,6578 | 2,123973 | 992,7753 | 1850,231 | 6794,784 |
| Интервал | 140-120 | 120-100 | 100-85 | 85-70 | 70-55 | 55-45 |
Среднее гармоническое взвешенное значение:
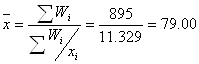 км/ч
км/ч
Показатели вариации:
- среднее линейное отклонение
 км/ч
км/ч
- дисперсия
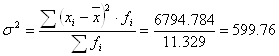 (км/ч)2
(км/ч)2
- среднее квадратическое отклонение
![]() км/ч
км/ч
- коэффициент вариации
![]()
Мода:
![]() км/ч
км/ч
Медиана:
 км/ч
км/ч
Ответ: средняя гармоническая равна 79.0 км/ч; коэффициент вариации равен 31%, что свидетельствует об неоднородности совокупности, мода равна 61.38 км/ч, медиана равна 75.04 км/ч.
2. Ряды динамики
Рядом динамики называется ряд чисел, характеризующих изменение общественного явления во времени. Значения показателей, образующих ряд динамики, называют уровнем ряда ![]() .
.
Для общей характеристики уровня явления за тот или иной период исчисляется средний уровень ряда. Способ расчета среднего уровня ряда зависит от характера ряда. Различают моментный и интервальный ряды динамики.
Моментным рядом называют ряд, который образуют показатели характеризующие состояние явления на тот или иной момент времени.
Интервальным рядом динамики называют ряд, который образуют показатели характеризующие явление за тот или иной период времени.
Средний уровень интервального ряда определяется по формуле:
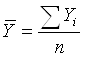 ,
,
где n – число членов ряда динамики.
Средний уровень моментного ряда определяют по формуле средней хронологической:
 .
.
Абсолютный прирост показывает на сколько единиц увеличился (или уменьшился) анализируемый уровень ряда относительно базисно уровня (по базисной схеме) или уровня предшествующего года (по цепной схеме). Соответственно его определяют по формулам:
![]() (по базисной схеме),
(по базисной схеме),
![]() (по цепной схеме).
(по цепной схеме).
Темп роста показывает, во сколько раз анализируемый уровень ряда увеличился (или уменьшился) по сравнению с уровнем принятым за базу сравнения (по базовой схеме) или предшествующим уровнем (по цепной схеме). Темп роста выражают в процентах или отвлеченных числах (коэффициент роста). Его определяют по формуле:
![]() (по базисной схеме),
(по базисной схеме),
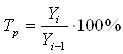 (по цепной схеме).
(по цепной схеме).
Темп прироста показывает, на сколько процентов увеличился (или уменьшился) анализируемый уровень ряда по сравнению с базисным (по базисной схеме), или предшествующим уровнем ряда (по цепной схеме). Его определяют как отношение абсолютного прироста к уровню, принятому за базу сравнения по формулам:
![]() (по базисной схеме),
(по базисной схеме),
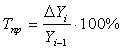 (по цепной схеме).
(по цепной схеме).
Темпы роста и прироста связаны между собой, что видно из формул их расчета:
![]()
Это дает основание определить темп прироста через темп роста:
![]() .
.
Средний темп роста и средний темп прироста характеризуют соответственно темпы роста и прироста за период в целом. Средний темп роста рассчитывается по данным ряда динамики по формуле средней геометрической:
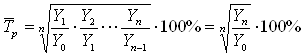 ,
,
где ![]() - количество цепных коэффициентов роста.
- количество цепных коэффициентов роста.
Исходя из соотношения темпов роста и прироста, определяется средний темп прироста:
![]() .
.
Абсолютное значение одного процента прироста А – это отношение цепного абсолютного прироста к цепному темпу прироста выраженному в процентах. Оно определяется по формуле:
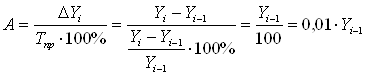 .
.
Как видно из расчета абсолютное значение одного процента прироста равно 0,01 предшествующего уровня.
С помощью ряда динамики изучают явления, имеющие сезонный характер. Сезонными колебаниями называют устойчивые внутригодовые колебания в ряду динамики, обусловленные специфическими условиями производства, потребления или продажи продукции или услуг. Например, потребление топлива или электроэнергии для бытовых нужд, перевозки пассажиров, продажи товаров и др.
Уровень сезонности оценивается с помощью индексов сезонности. Индекс сезонности показывает, во сколько раз фактический уровень ряда в момент или интервал времени больше среднего уровня. Он определяется по формуле:
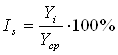 ,
,
где ![]() - уровень сезонности;
- уровень сезонности;
![]() - текущий уровень ряда динамики;
- текущий уровень ряда динамики;
![]() - средний уровень ряда.
- средний уровень ряда.
Графически индекс сезонности может быть представлен с помощью полигона – основного вида графиков, используемого для графического изображения рядов динамики.
Задание 3
По данным таблицы 3 вычислите:
1. Основные аналитические показатели рядов динамики (по цепной и базисным схемам):
- абсолютный прирост;
- темпы роста;
- темпы прироста;
- абсолютное значение 1 % прироста.
2. Показатели средних:
- средний уровень ряда динамики;
- среднегодовой темп роста;
- среднегодовой темп прироста.
Таблица 4
| Показатели | Годы | |||||
| 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | |
| Число посещений театров, млн. посещ. | 10,0 | 10,7 | 12,0 | 10,3 | 12,9 | 16,3 |
3. По данным таблицы 5 вычислите индекс сезонности и изобразите графически сезонную волну.
Таблица 5
| Месяц | Значение товарооборота, тыс. руб. |
| Январь | 12,78 |
| Февраль | 122,98 |
| Март | 277,12 |
| Апрель | 508,34 |
| Май | 418,31 |
| Июнь | 709,98 |
| Июль | 651,38 |
| Август | 1602,61 |
| Сентябрь | 521,18 |
| Октябрь | 327,68 |
| Ноябрь | 396,20 |
| Декабрь | 220,80 |
Решение
Рассчитаем показатели (таблица 6):
Таблица 6
| Показатели | Схема расчета | Годы | |||||
| 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | ||
| Уровень ряда, | - | 10,0 | 10,7 | 12,0 | 10,3 | 12,9 | 16,3 |
| Абсолютный прирост | базисная | - | 0,7 | 2 | 0,3 | 2,9 | 6,3 |
| цепная | - | 0,7 | 1.3 | -1,7 | 2,6 | 3,4 | |
| Темп роста, % | базисная | 100 | 107,00 | 120,00 | 103,00 | 129,00 | 163,00 |
| цепная | 100 | 107,00 | 112,15 | 85,83 | 125,24 | 126,36 | |
| Темп прироста, % | базисная | - | 7,00 | 20,00 | 3,00 | 29,00 | 63,00 |
| цепная | - | 7,00 | 12,15 | -14,17 | 25,24 | 26,36 | |
| Абсолютное значение одного процента прироста | цепная | - | 0,1 | 0,107 | 0,12 | 0,103 | 0,129 |
Показатели средних:
- средний уровень ряда динамики:
![]() млн. посещ.
млн. посещ.
- среднегодовой темп роста:

- среднегодовой темп прироста
![]()
Рассчитаем индексы сезонности по таблице 4 (таблица 7):
| Месяц | Значение товарооборота, тыс. руб. | Индекс сезонности, % |
| Январь | 12,78 | 2,66 |
| Февраль | 122,98 |
Подобные работы:
Актуально:
|