Оцінювання параметрів розподілів

ОЦІНЮВАННЯ ПАРАМЕТРІВ РОЗПОДІЛІВ

Задача оцінювання параметрів розподілів полягає в побудові на основі статистичної інформації, отриманої за даними вибірки, статистичних висновків про істинне значення невідомого параметра , в знаходженні величини , яку можна буде взяти в якості його оцінки, і в визначенні припустимих меж їхньої розбіжності.

1. Загальні положення теорії оцінювання параметрів розподілів

Оскільки існує велика кількість функцій від вибіркових значень, які можна використати як оцінки параметрів, для вибору найкращої оцінки необхідно ввести критерій порівняння якості оцінок, вибрати міру, яка характеризує близькість оцінки  до істинного значення параметра , який оцінюється. Проблема полягає в тому, що будь-яка оцінка, є величиною випадковою, тому що вона подає, собою функцію від вибірки обмеженого обсягу. Тому судити про її якість з реалізації тільки у даній вибірці не можна. Необхідно за законом розподілу оцінки, за формою кривої розподілу, з її розташування на числовій осі щодо оцінюваного параметра розсудити про те, або добре, чи незадовільно її підібрано.

Наприклад, на рис. 1 продемонстровано три криві розподілу оцінок різної якості під номерами 1- Очевидно, що розподіл типу 3 є дуже незадовільним, тому що середнє значення цієї оцінки є зміщеним вправо щодо істинного значення  і, отже, значення  буде оцінюватися із систематичною похибкою убік завищення. У розподілу цієї оцінки порівняно великим є і розсіювання.

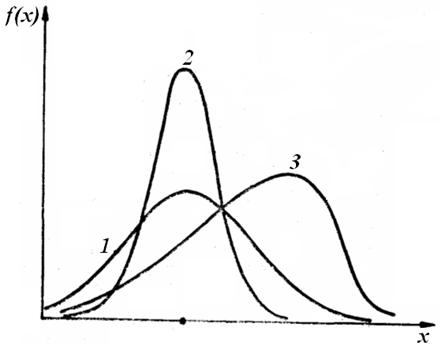
Рисунок 1 – Криві розподілу оцінок

Подібність розподілів оцінок 1 і 2 між собою полягає в тому, що їхні середні значення оцінок знаходяться біля істинного значення параметра а, тобто зміщення в оцінці параметра при цьому відсутні чи є незначними. Однак розподіл типу 2  має істотно меншу дисперсію в порівнянні з розподілом 1. Тобто розсіювання значень оцінки 2, отриманої за даними вибірки, щодо істинного значення параметра у цьому разі буде меншим, ніж для оцінки 1, тому її слід вважати кращою.

Функції результатів спостережень (вибірки), що використовують для оцінки параметрів розподілів, називаються статистиками. У цій термінології оцінкою параметра є статистика ; реалізація якої, отримана по даній вибірці, приймається за невідоме значення параметра .

.

Взагалі, відповідно до узагальненої теореми великих чисел у вигляді границі  ибіркова оцінка  називається обґрунтованою, якщо під час збільшення обсягу вибірки  вона збігається за ймовірністю до оцінюваного параметра .

Оцінка параметра  називається незміщеною, якщо математичне сподівання оцінки дорівнює оцінюваному параметру :

.

У противному випадку оцінка називається зміщеною.

Оцінка параметра  називається ефективною, якщо її дисперсія є мінімальною з усіх можливих дисперсій його оцінок:

Якщо зі збільшенням обсягу вибірки дисперсія оцінки прагне до будь-якого граничного (мінімального) значення, наприклад, як на рис. 2, оцінка називається асимптотично ефективною.

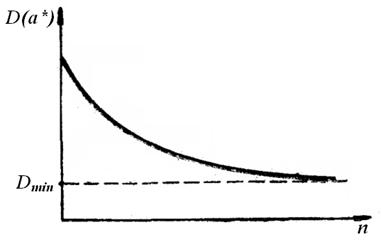
Рисунок 2 – Дисперсія асимптотично ефективної оцінки

Задовольнити всім трьом вимогам оцінки параметра розподілу (обґрунтованості, незміщеності та ефективності) разом звичайно не вдається. Насамперед це стосується спільного виконання останніх двох вимог.

Оцінювання параметра традиційно проводять у два етапи. На першому етапі визначають статистику , значення якої при даній реалізації вибірки приймають за наближене значення оцінюваного параметра : .

Цю процедуру в математичній статистиці називають точковим оцінюванням, а величину  – точковою оцінкою.

На другому етапі оцінюють точність і надійність точкової оцінки, яка за своєю природою є величиною випадковою. Ця процедура полягає в знаходженні інтервалу, де із заданою ймовірністю міститься невідоме значення параметра, що оцінюється. Цей етап звичайно називають інтервальним оцінюванням.

Далі розглянемо основні методи, що дозволяють провести точкове і інтервальне оцінювання параметрів.

2. Точкове оцінювання параметрів

Головними методами одержання точкових оцінок параметрів є метод моментів і метод максимальної правдоподібності.

Метод моментів. Цей метод (Пірсона) полягає в порівнюванні визначеної кількості вибіркових моментів, що співпадає з числом підлягаючих оцінці параметрів, з відповідними теоретичними моментами розподілу, що є функціями від невідомих параметрів. При розв’язанні системи рівнянь, що при цьому одержують, знаходять точкові оцінки параметрів.

Задля прикладу застосуємо метод моментів для визначення параметрів рівномірного закону розподілу випадкової величини  зі щільністю ймовірності, що задано функцією

                                    (1)

Обчислимо математичне сподівання і дисперсію величини :

,                               (2)

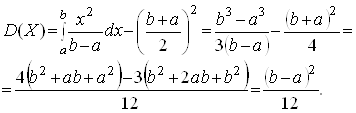                   (3)

Для визначення оцінок параметрів  і , тобто визначення  і  замінимо в рівняннях (2) і (3)  і  їхніми оцінками  і  (1),(2). Одержимо систему рівнянь для точкових оцінок , , 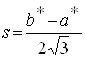звідки знаходимо:

.

Відомо, що метод моментів при досить загальних умовах дозволяє знайти оцінки, для яких виконується вимога асимптотичної ефективності. Однак, як доведено Фішером, отримані цим методом оцінки з погляду їхньої ефективності не є найкращими з можливих, тобто при великих вибірках вони мають не найменшу можливу дисперсію. Тому отримані цим методом оцінки слід роз­глядати лише як перше наближення.

Метод максимальної правдоподібності. Найбільш поширеним методом точкового оцінювання є метод максимальної правдоподібності (Фішера). Оцінки, отримані цим методом при досить великих вибірках, звичайно задовольняють усім перерахованим вище вимогам обґрунтованості, незміщеності та ефективності.

Сутність цього методу полягає у наступному. Нехай дана вибірка  обсягу  з генеральної сукупності з неперервно розподіленою випадковою величиною . Нехай щільність ймовірності  має вигляд , тобто містить невідомий параметр , який треба оцінити за вибіркою.

Функцією правдоподібності називають функцію параметра , що визначається формулою:

.                          (4)

У разі дискретної випадкової величини  з можливими значеннями  та ймовірностями  позначимо через  найбільше з можливих значень, що зустрічається у вибірці, а через  ­ абсолютні частоти, з якими з'являються значення , ,... у вибірці . У цьому випадку функцією правдоподібності називають функцію параметра , що задана співвідношенням

.                              (5)

Метод найбільшої правдоподібності полягає в тому, що за оцінку параметра береться таке його значення, при якому функція правдоподібності досягає свого максимуму.

Параметр  знаходять, розв’язуючи відносно нього рівняння

.                                              (6)

Часто для зручності функцію правдоподібності заміняють її логарифмом і замість (6) розв’язують рівняння вигляду

 ,   .                                           (7)

Якщо щільність ймовірності  або ймовірність можливого значення  залежать від  параметрів, то найбільш правдоподібну оцінку системи параметрів  одержують під час розв’язання системи рівнянь

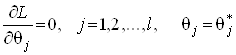                                     (8)

або

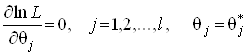.                                  (9)

Найбільш правдоподібні оцінки при досить загальних умовах мають такі важливі властивості:

– вони є обґрунтованими,

– асимптотично нормально розподіленими, однак не завжди незміщеними,

– серед усіх асимптотично нормально розподілених оцінок вони мають найбільшу ефективність.

Має місце також наступне положення: якщо взагалі є ефективна оцінка, її можна отримати методом найбільшої правдоподібності.

3. Інтервальне оцінювання параметрів

Інтервальною називають оцінку, що визначається двома числами – кінцями інтервалу. Інтервальні оцінки дозволяють визначити точність і надійність точкових оцінок.

Надійністю (довірчою ймовірністю) оцінки невідомого параметра  за допомогою знайденої за даними вибірки статистичної характеристики  називають ймовірність , з якою виконується нерівність :

чи, що те ж саме

.

Звичайно використовують рівень надійності, що має значення: 0,95; 0,99 і 0,999.

Довірчим називають інтервал ( ), який покриває невідомий параметр із заданою надійністю .

1 Довірчі інтервали для оцінки математичного сподівання нормаль­ного розподілу при відомому . Розглянемо задачу інтервальної оцінки невідомого математичного сподівання  кількісної ознаки  по вибірковій
середній  нормально розподіленої сукупності з відомим середньо квадратич­ним відхиленням . Знайдемо довірчий інтервал, що покриває параметр  з надійністю .

Вибіркова середня  змінюється від вибірки до вибірки. Тому її можна розглядати, як випадкову величину , а вибіркові значення ознаки , , ... ,  (ці числа також змінюються від вибірки до вибірки) – як однаково розподілені незалежні випадкові величини , , ... , . Тобто, математичне сподівання кожної з цих величин дорівнює  і середнє квадратичне відхилення – .

Можна показати, що у разі нормального розподілення випадкової величина  вибіркова середня , знайдена за незалежними спостереженнями, також розподілена нормально з параметрами:

, .                                        (12)

Поставимо вимогу, щоб було виконано співвідношення

,                                                (13)

де  – задана надійність.

Застосуємо до нормально розподіленої випадкової величини  відому з теорії ймовірностей формулу про ймовірність відхилення нормально розподіленої випадкової величини  зі середньоквадратичним відхиленням  від його математичного сподівання  не більше ніж на

 ,                                   (14)

де  – табульована функція Лапласа (3).

При цьому у формулі (14) відповідно до (12) необхідно замінити  на ,  на , залишивши математичне чекання  без зміни.

Тоді одержимо:

,                            (15)

де введено таке позначення

.                                                (16)

Підставивши у формулу (15) вираз величини  через  з (16)

,                                                 (17)

перетворивши її до вигляду:

.

З огляду на те, що ймовірність  задана і дорівнює  (13), а також, що випадкова величина  є формальним поданням вибіркової середньої , остаточно одержимо:

.                       (18)

Цю оцінку називають класичною. Відповідно до неї з надійністю  можна стверджувати, що довірчий інтервал  покриває невідомий параметр . При цьому величина  визначається з рівності (18), а точність оцінки  – з (17).

З формули (17) видно, що із зростанням обсягу вибірки  величина  зменшується, тобто точність оцінки підвищується. З співвідношення (18), де , із врахуванням відомого зростаючого характеру функції Лапласа  (3), випливає, що підвищення надійності класичної оцінки (18) призводить до погіршення її точності.

2 Довірчі інтервали для оцінки математичного сподівання нормального розподілу при невідомому . Ускладнимо постановку задачі, розглянутої в попередньому пункті, вважаючи, що тепер середнє квадратичне відхилення  нормально розподіленої кількісної ознаки  невідомо.

У цьому випадку за даними вибірки побудуємо випадкову величину  (її значення будемо традиційно позначати відповідною малою буквою ), що є функціональним перетворенням випадкової величини , введеної в попередньому пункті:

 .                                                  (19)

Тут збережено позначення, які введені в попередньому пункті. Крім того, вжито , що є "виправлене" середнє квадратичне відхилення (1.7).

Можна показати, що випадкова величина  (19) має розподіл Стьюдента (2.8) з  ступенями волі і щільністю розподілу:

,

Де

,

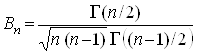 – Гама-функція Эйлера (2.4).

Очевидно, що розподіл Стьюдента визначається параметром  – обсягом вибірки та не залежить від невідомих параметрів  і , що зумовило його практичну цінність. Оскільки функція  є парною відносно , ймовірність виконання нерівності 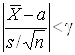 можна перетворити таким чином:

.

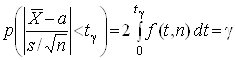При заміні нерівності в круглих дужках на еквівалентну йому подвійну нерівність і заміні  на  так само, як у попередньому пункті, остаточно  одержимо:

.

Тобто, використовуючи розподіл Стьюдента, можна знайти довірчий інтервал , що покриває невідомий параметр  із надійністю . Величина  при цьому знаходиться в таблиці розподілу Стьюдента  у залежності від значень параметрів  і .

3 Довірчі інтервали для оцінки середнього квадратичного відхилення  нормального розподілу. Тепер вирішимо задачу інтервальної оцінки з надійністю  невідомого генерального середнього квадратичного відхилення  нормально розподіленої кількісної ознаки  за його "виправленим" вибірковим середньо квадратичним відхиленням s. Це означає, що має виконуватися умова:

чи, що те ж саме,

.                                          (20)

Подвійну нерівність у виразі (20) зручно перетворити до вигляду:

                                           (21)

,                                       (22)

де введено позначення

                                                  (23)

і враховано, що відхилення  відносно , тобто  – мала величина в порівнянні з , так що .

Вибіркове середнє квадратичне відхилення  змінюється від вибірки до вибірки, тому його можна розглядати як випадкову величину, що ми дотримуючись традиції позначимо відповідною великою літерою . Помноживши всі члени останньої нерівності (22) на , одержимо нову нерівність

,

що після введення позначення

                                              (24)

прийме остаточний вигляд:

.                                           (25)

Відзначимо, що нерівності (21) і (25) еквівалентні. Тому рівність (20) можна тепер переписати так:

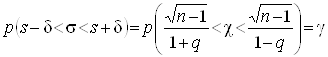.                    (26)

Пірсон показав, що величина  (24) після її підвищення до квадрату, тобто у вигляді , підкоряється закону розподілу "хі-квадрат" (5), тому і має таке позначення. Можна показати, що щільність розподілу самої випадкової величини  має при цьому наступний вигляд:

 .                                    (27)

Важлива особливість цього розподілу полягає в тому, що воно є інваріантним відносно оцінюваного параметра , і залежить лише від обсягу вибірки .

Відомо, що ймовірність неперервній випадковій величині  знаходитися на інтервалі ( , ) виражається у такий спосіб через щільність її розподілу:

.

Застосувавши цю формулу в нашому конкретному випадку ймовірності перебування випадкової величини  (24) із щільністю у вигляді (27) на інтервалі (25), одержимо:

.                        (28)

Співвідношення (28) можна розглядати як рівняння щодо невідомої величини  (23) при заданих значеннях  і . Це рівняння було розв’язано в загальному вигляді зі складанням таблиць, по яких можна знайти значення . Знаючи величину  і "виправлене" вибіркове середнє квадратичне відхилення s по формулам (21), (23) визначаємо довірчий інтервал для оцінки середнього квадратичного відхилення  нормального розподілу.

4 Оцінки істинного значення величини, що вимірюється, і точності вимірів. Ця задача подає великий практичний інтерес для метрології.

Нехай проведено  незалежних однаково точних вимірів деякої фізичної величини, істинне значення  якої невідомо. До того ж невідомо також і середнє квадратичне відхилення  випадкових похибок вимірювання. Результати окремих вимірів , , ... ,  можна розглядати, як випадкові величини , , ... , , що є незалежні (виміри незалежні), мають те ж саме математичне сподівання  (істинне значення величини, що вимірюється), однакові дисперсії  (виміри однаково точні) і нормально розподілені (таке допущення підтверджується досвідом).

Отже, усі припущення, що було зроблено під час отримання довірчих інтервалів у пунктах 1 і 2, виконуються. Тому можна безпосередньо використати отримані в них формули. Іншими словами, істинне значення величини, що вимірюється, можна оцінювати по середньому арифметичному результатів окремих вимірів за допомогою довірчих інтервалів.

Середнє квадратичне відхилення  випадкових похибок вимірів у теорії помилок характеризує точність вимірів (точність приладу).

Для оцінки  використовують "виправлене" середнє квадратичне відхилення . Оскільки звичайно результати вимірів взаємно незалежні, мають одне й теж саме математичне сподівання (істинне значення величини, що вимірюється) і однакову дисперсію (у випадку однаково точних вимірів), то теорію, викладену в пункті 3, можна застосувати і для оцінки точності вимірів.

5 Інтервальна оцінка ймовірності біноміального розподілу. У підрозділі 2 у якості приклада 1 було вирішено задачу точкової оцінки ймовірності біноміального розподілу. Як точкову оцінку невідомої ймовірності  було узято відносну частоту  появи події ( – число появ події,  – число випробувань). Було отримано математичне сподівання і дисперсію оцінки.

Тепер буде знайдено довірчий інтервал для оцінки ймовірності за відносною частотою.

Для спрощення припустимо, що кількість іспитів  досить велика, а ймовірність  не є близькою ні до одиниці, ні до нуля (досить, щоб обидві величини  і  були більше чотирьох). Тоді можна вважати, що частота події  є випадковою величиною , розподіл якої є наближеним до нормального закону (у сенсі функції розподілу). Параметрами цього закону будуть  і .

Тому до випадкової величини  можна застосувати відому формулу про ймовірність відхилення нормально розподіленої випадкової величини  зі середньо квадратичним відхиленням  від її математичного сподівання  не більше ніж на

 ,                                    (29)

де  – табульована функція Лапласа.

Зажадавши, щоб умова для ймовірності у формулі (29) виконувалося з надійністю , і, замінивши в ній  на ,  на ,  на , а також увівши позначення 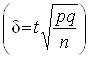, одержимо

або інакше

.

При практичному застосуванні цієї формули випадкову величину  необхідно замінити невипадковою відносною частотою , що спостерігається, і підставити :

.

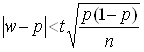Під час розв’язання цієї нерівності щодо невідомої ймовірності  у припущенні  підвищимо до квадрата обидві її частини. При цьому одержимо еквівалентну квадратну нерівність відносно :

.

Її коефіцієнт при старшому члені та дискримінант позитивні, тому її корені  і  дійсні, причому не дорівнюють один одному. Отже ця нерівність має розв’язання:

,

дисперсія крива розподіл сподівання

що і визначає довірчий інтервал, який слід знайти.

Аналогічний розв’язок нерівності отримуємо і у разі .