Дифференцирование в линейных нормированных пространствах
Основные понятия
Сильный дифференциал (дифференциал Фреше)
Слабый дифференциал (дифференциал Гато)
Формула конечных приращений
Связь между слабой и сильной дифференцируемостью
Дифференцируемые функционалы
Абстрактные функции
Интеграл
Производные высших порядков
Дифференциалы высших порядков
Формула Тейлора
Заключение1
Список литературы:
Введение
Функциональный анализ — раздел математики, в котором изучаются бесконечномерные пространства и их отображения.
Понятие нормированного пространства – одно из самых основных понятий функционального анализа. Теория нормированных пространств была построена, главным образом, С. Банахом в 20-х годах 20 века. Функциональный анализ за последние два десятилетия настолько разросся, настолько широко и глубоко проник почти во все области математики, что сейчас даже трудно определить самый предмет этой дисциплины. Однако в функциональном анализе есть несколько больших «традиционных» направлений, которые и поныне в значительной степени определяют его лицо. К их числу принадлежит дифференцирование линейных нормированных пространств.
Основные понятия
Определение 1. Непустое множество ![]() называется линейным пространством, если оно удовлетворяет следующим условиям:
называется линейным пространством, если оно удовлетворяет следующим условиям:
Й. Для любых двух элементов ![]() однозначно определен элемент
однозначно определен элемент ![]() , называемый их суммой, причем
, называемый их суммой, причем
1. ![]() (коммутативность)
(коммутативность)
2. ![]() (ассоциативность)
(ассоциативность)
В ![]() существует такой элемент 0, что
существует такой элемент 0, что ![]() для всех
для всех ![]()
4. Для каждого ![]() существует такой элемент
существует такой элемент ![]() , что
, что ![]() .
.
II. Для любого числа ![]() и любого элемента
и любого элемента ![]() определен элемент
определен элемент ![]() , причем
, причем
5. ![]()
6. ![]()
III. Операции сложения и умножения связаны между собой дистрибутивными законами:
7. ![]()
8. ![]()
Определение 2. Линейное пространство ![]() называется нормированным, если на нем задана неотрицательная функция
называется нормированным, если на нем задана неотрицательная функция ![]() , называемая нормой, удовлетворяющая условиям:
, называемая нормой, удовлетворяющая условиям:
![]()
![]()
для любого ![]() и любого числа
и любого числа ![]() ;
;
![]()
для любых ![]() (неравенство треугольника).
(неравенство треугольника).
Определение 3. Оператором называется отображение
![]() ,
,
где ![]() - это линейные пространства.
- это линейные пространства.
Определение 4. Оператор ![]()
![]() называется линейным, если для любых элементов
называется линейным, если для любых элементов ![]() и любых чисел
и любых чисел ![]() R выполняется равенство:
R выполняется равенство:
![]()
Определение 5. Пусть ![]() - линейные нормированные пространства,
- линейные нормированные пространства,
![]()
![]() – линейный оператор,
– линейный оператор,
![]()
Линейный оператор непрерывен в точке![]() , если из того, что
, если из того, что
![]() следует, что
следует, что ![]() .
.
Определение 6. Линейный оператор ![]() непрерывен, если он непрерывен в каждой точке
непрерывен, если он непрерывен в каждой точке ![]() .
.
Определение 7. Линейный оператор называется ограниченным, если
![]()
![]()
![]()
Утверждение. Для линейного нормированного пространства непрерывность линейного оператора равносильна его ограниченности.
Определение8. Наименьшая из констант M таких, что ![]() , называется нормой оператора А и обозначается
, называется нормой оператора А и обозначается ![]() .
.
В частности, выполняется
![]()
Справедливо следующее утверждение: для любого ограниченного линейного оператора
![]()
![]()
Пусть X и У — два нормированных пространства и F — отображение, действующее из X в Y и определенное на некотором открытом подмножестве О пространства X. Мы назовем это отображение дифференцируемым в данной точке![]() , если существует такой ограниченный линейный оператор Lx
, если существует такой ограниченный линейный оператор Lx![]() ж (X, Y), что для любого е> 0 можно найти д > 0, при котором из неравенства ||h||< д следует неравенство
ж (X, Y), что для любого е> 0 можно найти д > 0, при котором из неравенства ||h||< д следует неравенство
|| F(x + h)-F(x)-Lxh ||<е||h|| (1)
То же самое сокращенно записывают так:
А(ч + р)-А(ч)-Дчр = щ(р)ю(2)
Из (I) следует, что дифференцируемое в точке х отображение непрерывно в этой точке. Выражение Lxh (представляющее собой, очевидно, при каждом h![]() X элемент пространства У) называется сильным дифференциалом (или дифференциалом Фреше) отображения F в точке х. Сам линейный оператор Lxназывается производной, точнее, сильной производной отображения F в точке х. Мы будем обозначать эту производную символом F'(x).
X элемент пространства У) называется сильным дифференциалом (или дифференциалом Фреше) отображения F в точке х. Сам линейный оператор Lxназывается производной, точнее, сильной производной отображения F в точке х. Мы будем обозначать эту производную символом F'(x).
Если отображение F дифференцируемо в точке, то соответствующая производная определяется единственным образом. В самом деле, равенство
||L1h — L2h|| = o(h) для операторов
Li![]() ж (X, У), i = 1, 2,
ж (X, У), i = 1, 2,
возможно, лишь если L1= L2.
Установим теперь некоторые элементарные факты, непоcредственно вытекающие из определения производной.
Если F(x) = y0 = const, то F'(x) = О (т. е. F'(х)
в этом случае есть нулевой оператор).
Производная непрерывного линейного отображения L есть само это отображение:
L '(x)=L(3)
Действительно, по определению имеем
L(x + h)-L(x) = L(h).
3. (Производная сложной функции). Пусть X, У, Z — три нормированных пространства, U(x0)—окрестность точки х0![]() Х, F — отображение этой окрестности в У, у0 = F(x0), V(yo) — окрестность точки у0
Х, F — отображение этой окрестности в У, у0 = F(x0), V(yo) — окрестность точки у0![]() У и G — отображение этой окрестности в Z. Тогда, если отображение F дифференцируемо в точке хо, a G дифференцируемо в точке уо, то отображение Н = GF (которое определено в некоторой окрестности точки х0) дифференцируемо в точке хо и
У и G — отображение этой окрестности в Z. Тогда, если отображение F дифференцируемо в точке хо, a G дифференцируемо в точке уо, то отображение Н = GF (которое определено в некоторой окрестности точки х0) дифференцируемо в точке хо и
H' (x0)=G' (y0)F' (x0) (4)
Действительно, в силу сделанных предположений
А(ч0 +о) = А(ч0) + Аэ (ч0) о +о1 (о ) и
G (уо + з) = G (уо) + G' (уо) з + о2 (з).
НоF'(x0) иG'(yo) — ограниченные линейные операторы. Поэтому
H (х0 + о) = G (уо + F' (x0) о + о1 о ) = G (уо) + G' (у0) (F' (х0) о + +о1 о)) +
+о2 (F' (x0) о + о1 (о )) = G (у0) + G' (уо) F' (х0) о + о3 (о).
Если F, G и Н — числовые функции, то формула (4) превращается в известное правило дифференцирования сложной функции.
4. Пусть F и G — два непрерывных отображения, действующих из X в Y. Если F и G дифференцируемы в точке х0, то и отображения F + G и aF (а — число) тоже дифференцируемы в этой точке, причем
(F + G)'(х0) = F'(х0) + G'(х0) (5)
(aF)'(x0) = aF'(x0).(6)
Действительно, из определения суммы операторов и произведения оператора на число сразу получаем, что
(F+G)(x0 + h) = F(x0 + h) + G(x0 + h) = F (х0) + G (х0) + F' (х0) h +
+G' (х0) h + o1 (h) и
aF (x0 + h) = aF (x0) + aF' (x0) h + o2 (h),
откуда следуют равенства (5) и (6).
Слабый дифференциал (дифференциал Гато)
Пусть снова F есть отображение, действующее из X в У. Слабым дифференциалом или дифференциалом Гато отображения F в точке х (при приращении h) называется предел
DF(x,h)=![]() t=0=
t=0=![]()
![]()
![]() ,
,
где сходимость понимается как сходимость по норме в пространстве У.
Иногда, следуя Лагранжу, выражение DF(x,h) называют первой вариацией отображения F в точке х.
Слабый дифференциал DF(x,h) может и не быть линеен по h. Если же такая линейность имеет место, т. е. если
DF (х, h) = F'c (х) h,
где F'c (х) — ограниченный линейный оператор, то этот оператор называется слабой производной (или производной Гато).
Заметим, что для слабых производных теорема о дифференцировании сложной функции, вообще говоря, неверна.
Формула конечных приращенийПусть О — открытое множество в X и пусть отрезок (х0, х) целиком содержится в О. Пусть, наконец, F есть отображение X в У, определенное на О и имеющее слабую производную F'c в каждой точке отрезка (х0, x). Положив Дх = х — хо и взяв произвольный функционал ![]() У*, рассмотрим числовую функцию
У*, рассмотрим числовую функцию
f(t) = ![]() (F(x0+t Дх)),
(F(x0+t Дх)),
определенную при ![]() .Эта функция дифференцируема по t. Действительно, в выражении
.Эта функция дифференцируема по t. Действительно, в выражении
![]()
можно перейти к пределу под знаком непрерывного линейного функционала![]() . В результате получаем
. В результате получаем
F'(t) = ![]() (F'c(x0+tДx) Дx)
(F'c(x0+tДx) Дx)
Применив к функции f на отрезке (0, 1) формулу конечных приращений, получим
f(l) = f(0) + f'(и), где 0< и <1,
![]() (F(x)-F(x0))=
(F(x)-F(x0))= ![]() ( F'c(x0+ и Дx) Дx)(7)
( F'c(x0+ и Дx) Дx)(7)
Это равенство имеет место для любого функционала ![]() У* (величина и зависит, разумеется, от
У* (величина и зависит, разумеется, от![]() ). Из (7) получаем
). Из (7) получаем
|![]() (F(x)-F(x0))|
(F(x)-F(x0))|![]()
![]()
![]() || F'c(x0+ и Дx)||
|| F'c(x0+ и Дx)|| ![]() || Дx|| (8)
|| Дx|| (8)
Выберем теперь ненулевой функционал ![]() так, что
так, что
![]() (F (х) - F (х0)) =
(F (х) - F (х0)) =![]()
![]() F(х) - F (хо) ||
F(х) - F (хо) ||
(такой функционал ![]() существует в силу следствия 4 теоремы Хана — Банаха (см. п. 3 § 1 гл. IV)). При этом из (8) получаем
существует в силу следствия 4 теоремы Хана — Банаха (см. п. 3 § 1 гл. IV)). При этом из (8) получаем
||(F (х) - F (x)||![]()
![]() F'c(x0+ и Дx)||
F'c(x0+ и Дx)|| ![]() ||Дx|| (Дx=x-x0) (9)
||Дx|| (Дx=x-x0) (9)
Это неравенство можно рассматривать как аналог формулы конечных приращений для числовых функций. Применив формулу (9) к отображению
х —Ю А (х) — Аэс (хо) Дч
получим следующее неравенство:
||F(x-F(хо)-F'c(хо) Дx![]()
![]() F'c(xo+иДx) -F'c(x0)||
F'c(xo+иДx) -F'c(x0)||![]() || Дx (10)
|| Дx (10)
Связь между слабой и сильной дифференцируемостью
Сильная и слабая дифференцируемость представляют собой различные понятия даже в случае конечномерных пространств. Действительно, из анализа хорошо известно, что для числовой функции
f(x) = f(x1,…,xn)
при n![]() 2 из существования производной
2 из существования производной
![]()
при любом фиксированном h = (f1,...,fn) еще не следует диф- ференцируемость этой функции, т. е. возможность представить ее приращение f(x+h)- f(x) в виде суммы линейной (по h) части и члена выше первого порядка малости относительно h.
Простейшим примером здесь может служить функция двух переменных
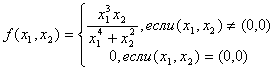 (11)
(11)
Эта функция непрерывна всюду на плоскости, включая точку (0,0). В точке (0,0) ее слабый дифференциал существует и равен 0, поскольку
![]()
Вместе с тем этот дифференциал не является главной линейной частью приращения функции (11) в точке (0,0). Действительно, если положить h2=h12, то
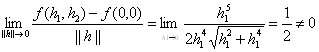
Однако если отображение F имеет сильную производную, то оно имеет и слабую, причем сильная и слабая производные совпадают. Действительно, для сильно дифференцируемого отображения имеем
А(ч + ер) — А (ч) = Аэ (ч) (ер) + о (ер) = еАэ (ч)р +о (ер) и
![]()
Выясним условия, при которых из слабой дифференцируемости отображения F следует его сильная дифференцируемость.
Теорема 1. Если слабая производная F'c (х) отображения F существует в некоторой окрестности U точки х0 и представляет собой в этой окрестности (операторную) функцию от х, непрерывную в x0, то в точке x0 сильная производная F'(x0) существует и совпадает со слабой.
Доказательство. По е>0 найдем д>0 так, чтобы при ||h||< д бвыполнялось неравенство:
|| F'c(xo + h)-F'c(xo) || ![]() е
е
Применив к отображению F формулу (10), получим:
F(x0 + h)-F (хо) - F'c(хо) h || ![]()
![]() ||F'c(xo+ иh)- F'c(xo)||
||F'c(xo+ иh)- F'c(xo)||
||h||![]() е||h||
е||h||
Тем самым имеет место теорема 1, т. е. доказано как существование сильной производной F'(xо), так и ее совпадение со слабой производной.
Дифференцируемые функционалы
Мы ввели дифференциал отображения F, действующего из одного нормированного пространства X в другое нормированное пространство У. Производная F'(х) такого отображения при каждом х — это линейный оператор из X в У, т. е. элемент пространства о(X, У). В частности, если У — числовая прямая, то F — принимающая числовые значения функция на X, т. е. функционал. При этом производная функционала F в точке х0 есть линейный функционал (зависящий от х0), т. е. элемент пространства X*.
Пример. Рассмотрим в действительном гильбертовом пространстве Н функционал F(x) = ||х||2. Тогда
||x + h||2-||x||2 = 2(x, h) + || h ||2;
величина 2(x,h) представляет собой главную линейную (по h) часть этого выражения, следовательно,
F' (x) = F'c(x) = 2х.
Абстрактные функции
Предположим теперь, что к числовой прямой сводится пространство аргументов X. Отображение F(x), сопоставляющее числу х элемент некоторого банахова пространства У, называется абстрактной функцией. Производная F'(х) абстрактной функции (если она существует) представляет собой (при каждом х) элемент пространства У — касательный вектор к кривой F(x). Для абстрактной функции (представляющей собой функцию одного числового аргумента) слабая дифференцируемость совпадает с сильной.
Интеграл
Пусть F — абстрактная функция действительного аргумента t со значениями в банаховом пространстве У. Если F задана на отрезке (а, b), то можно определить интеграл функции F по отрезку (а,b). Этот интеграл понимается как предел интегральных сумм
![]() ,
,
отвечающих разбиениям
ф = е0Бе1Б ююю Бет = иб ол![]() хелбел+1ъб
хелбел+1ъб
при условии, что max(tk+1-tk)![]() 0. Интеграл (представляющий, собой, очевидно, элемент из Y) обозначается символом
0. Интеграл (представляющий, собой, очевидно, элемент из Y) обозначается символом
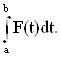
Рассуждения, в значительной мере аналогичные проводимым для функций, принимающих скалярные значения, показывают, что интеграл от функции, непрерывной на отрезке, существует; при этом он обладает свойствами обычного риманова интеграла.
Производные высших порядков
Пусть F — дифференцируемое отображение, действующее из X в У. Его производная F'(x) при каждом x![]() X есть элемент из о (X, У), т. е. F' есть отображение пространства X в пространство линейных операторов о (Х, У). Если это отображение дифференцируемо, то его производная называется второй производной отображения F и обозначается символом F". Таким образом, F"(x) есть элемент пространства о (Х, о (Х, У)) линейных операторов, действующих из X в о (X, У). Покажем, что элементы этого пространства допускают более удобную и наглядную интерпретацию в виде так называемых билинейных отображений.
X есть элемент из о (X, У), т. е. F' есть отображение пространства X в пространство линейных операторов о (Х, У). Если это отображение дифференцируемо, то его производная называется второй производной отображения F и обозначается символом F". Таким образом, F"(x) есть элемент пространства о (Х, о (Х, У)) линейных операторов, действующих из X в о (X, У). Покажем, что элементы этого пространства допускают более удобную и наглядную интерпретацию в виде так называемых билинейных отображений.
Мы говорим, что задано билинейное отображение пространства X в пространство У, если каждой упорядоченной паре элементов х, х' из X поставлен в соответствие элемент у=В(х, х') ![]() У так, что выполнены следующие условия:
У так, что выполнены следующие условия:
1. для любых ![]() из X и любых чисел
из X и любых чисел ![]() имеют место равенства:
имеют место равенства:
В (![]() x1 +
x1 + ![]() х2,
х2, ![]() ) =
) =![]() В (
В (![]() ,
,![]() )+
)+![]() В (х2,
В (х2, ![]() ),
),
В (x1, ![]()
![]() +
+![]()
![]() ) =
) = ![]() В (
В (![]() ,
,![]() )+
)+![]() В(x1,
В(x1,![]() );
);
2. существует такое положительное число М, что
||В(х, х') || ![]() M||x||
M||x||![]() ||x’|| (17)
||x’|| (17)
при всех х, х'![]() X.
X.
Первое из этих условий означает, что отображение В линейно по каждому из двух своих аргументов; нетрудно показать, что второе условие равносильно непрерывности В по совокупности аргументов.
Наименьшее из чисел М, удовлетворяющих условию (17), называется нормой билинейного отображения В и обозначается ||В||.
Линейные операции над билинейными отображениями определяются обычным способом и обладают обычными свойствами.
Таким образом, билинейные отображения пространства X в пространство У сами образуют линейное нормированное пространство, которое мы обозначим В(Х2, У). При полноте У полно и В(Х2, У).
Каждому элементу А из пространства о(Х,о(Х,У)) можно поставить в соответствие элемент из В(Х2, У), положив
В(х, х') = (Ах)х'.(18)
Очевидно, что это соответствие линейно. Покажем, что оно также и изометрично и отображает пространство о(X,о(Х,У)) на все пространство B(X2,Y). Действительно, если у=В(х, х') = (Ах)х', то
||y||![]() ||Ax||
||Ax||![]() ||x’||
||x’||![]() ||A||
||A||![]() ||x||
||x||![]() ||x’||,
||x’||,
откуда
||B||![]() ||A||(19)
||A||(19)
С другой стороны, если задано билинейное отображение В, то при фиксированном x![]() Xотображение
Xотображение
х'→ (Ах)х' = В(х, х')
есть линейное отображение пространства X в У.
Таким образом, каждому x![]() X ставится в соответствие элемент Ах пространства о(X, У); очевидно, что Ах линейно зависит от х, т. е. билинейное отображение В определяет некоторый элемент А пространства о(Х, о(Х, У)). При этом ясно, что отображение В восстанавливается по А при помощи формулы (18) и
X ставится в соответствие элемент Ах пространства о(X, У); очевидно, что Ах линейно зависит от х, т. е. билинейное отображение В определяет некоторый элемент А пространства о(Х, о(Х, У)). При этом ясно, что отображение В восстанавливается по А при помощи формулы (18) и
||Ах||= ![]() ||(Ax)x'||=
||(Ax)x'||=![]() ||В(х,x')
||В(х,x') ![]() ||B||
||B|| ![]() ||x||,
||x||,
Откуда
||A||![]() ||B||(20)
||B||(20)
Сопоставляя (19) и (20), получаем||A|| = ||В||. Итак, соответствие между B(X2,Y) и о{X, о(X,Y)), определяемое равенством (18), линейно и изометрично, а следовательно, взаимно однозначно. При этом образ пространства о(Х, о(Х, У)) есть все В(Х2, У).
Мы выяснили, что вторая производная F"(x) есть элемент пространства о(X, о (X, У)). В соответствии с только что сказанным мы можем считать F"(x) элементом пространства В(Х2, Y).
Очевидным образом можно ввести понятие третьей, четвертой и вообще п-й производной отображения F, действующего из X в Y, определив п-ю производную как производную от производной (п—1)-го порядка. При этом, очевидно, п-я производная представляет собой элемент пространства о(Х, о(Х, ..., о(X, У))). Повторяя рассуждения, проведенные для второй производной, можно каждому элементу этого пространства естественным образом поставить в соответствие элемент пространства N(Хп, У) n-линейных отображений X в У.
При этом под n-линейным отображением понимается такое соответствие y=N(x', х", ..., x(n)) между упорядоченными системами (х', х", .. . , x(n)) элементов из X и элементами пространства У, которое линейно по каждому из хi при фиксированных остальных элементах и удовлетворяет при некотором М > 0 условию
|| N (x', х", ..., x(n)) ||![]() М || х' || • || х" || ... || x(n) ||.
М || х' || • || х" || ... || x(n) ||.
Таким образом, п-ю производную отображения F можно считать, элементом пространства N(Xn,У).
Дифференциалы высших порядков
Мы определили (сильный) дифференциал отображения F как результат применения к элементу h![]() Х линейного оператора F'(x), т. е.
Х линейного оператора F'(x), т. е.
dF = F'(x)h
Дифференциал второго порядка определяется как
d2F = F" (х) (h, h),
т. е. как квадратичное выражение, отвечающее отображению
F''(х)![]() В(X2, У)
В(X2, У)
Аналогично дифференциалом п-го порядка называется
dnF=F(n)(x)(h, h, h),
т. е. тот элемент пространства У, в который элемент (h, h, ..., h) ![]()
![]() переводится отображением F(n)(x).
переводится отображением F(n)(x).
Формула Тейлора
Сильная дифференцируемость отображения F означает, что разность
F(x+h)—F(x)
может быть представлена в виде суммы линейного члена и слагаемого, имеющего порядок выше первого относительно ||h||. Обобщением этого факта является формула, аналогичная формуле Тейлора для числовых функций.
Теорема 2. Пусть F — отображение, действующее из X в У, определенное в некоторой области О![]() X и такое, что F(n)(x) существует и представляет собой равномерно непрерывную функцию от х в О. Тогда имеет место равенство
X и такое, что F(n)(x) существует и представляет собой равномерно непрерывную функцию от х в О. Тогда имеет место равенство
f(x + h)-F(x) = F'(x)h + ![]() F"(x)(h, h)+ ...
F"(x)(h, h)+ ...
... +![]() F(n)(x)(h,…,h) + щ (х, h), (21)
F(n)(x)(h,…,h) + щ (х, h), (21)
где
![]()
Доказательство будем вести по индукции. При n = 1 равенство (21) тривиально. Возьмем теперь произвольное фиксированное n и предположим, что равенство, получающееся из (21) заменой n на n-1, уже доказано для всех отображений, удовлетворяющих условиям теоремы, в которых n заменено на п-1. Тогда для отображения F' имеем
F'(x + h) = F'(x) + F"(x)h +![]() F"'(x)(h,h) + ...
F"'(x)(h,h) + ...
… + ![]() F(n)(x)(h,…,h) + щ1 (х, h), (22)
F(n)(x)(h,…,h) + щ1 (х, h), (22)
где
||щ1 (х, h)|| = o(||h||n-1)
Интегрируя обе части равенства (22) по отрезку (х, x+h) и пользуясь формулой Ньютона — Лейбница (15), мы получим
![]()
![]() , (21)
, (21)
Где
![]() .
.
из (23) получаем
А(ч+ р)-А (х)= Аэ(ч)р + ![]() АЭ(ч)(рбр)+ ююю
АЭ(ч)(рбр)+ ююю
…+![]() F(n)(x)(h,…,h) + Rn, причем
F(n)(x)(h,…,h) + Rn, причем
||Rn||![]()
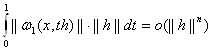
Тем самым наше утверждение доказано.
Формулу (21) называют формулой Тейлора для отображений.
Заключение
В этой работе представлены некоторые первоначальные понятия , относящиеся к нелинейному функциональному анализу, в основном к теории дифференцирования, и некоторые применения этих понятий.
Некоторые задачи, возникающие в функциональном анализе, носят существенно нелинейный характер; они приводят к необходимости развивать наряду с «линейными» и « нелинейными» функциональный анализ, т.е изучать нелинейные функционалы и нелинейные операторы в бесконечномерных пространствах.
К нелинейному функциональному анализу относится, по существу, такая классическая область математики, как вариационное исчисление, основы которого были заложены еще в XVII-XVIII вв. в работах Бернулли, Эйлера, Лагранжа. Однако в целом нелинейный функциональный анализ представляет собой сравнительно новую область математики, пока еще далекую от своего завершения.
Список литературы:
1. Колмогоров А.Н., Фомин С.В. - Элементы теории функций и функционального анализа. М., Наука, 1981. – 475 с.
2. Шилов Г.Е. – Дифференцирование функций в линейном пространстве. Ярославль, 1978. – 118стр.
3. Банах С. – Дифференциальное и интегральное исчисление. М.,Наука, 1972. – 424стр.