Кредиты от коммерческого банка на жилищное строительство
Задание 1
Приведены поквартальные данные о кредитах от коммерческого банка на жилищное строительство (в условных единицах) за 4 года (всего 16 кварталов, первая строка соответствует первому кварталу первого года).
Требуется:
1) Построить адаптивную мультипликативную модель Хольта-Уинтерса с учетом сезонного фактора, приняв параметры сглаживания a1=0,3; a2=0,6; a3=0,3.
2) Оценить точность построенной модели с использованием средней относительной ошибки аппроксимации.
3) Оценить адекватность построенной модели на основе исследования:
- случайности остаточной компоненты по критерию пиков;
- независимости уровней ряда остатков по d-критерию (критические значения d1 = 1,10 и d2 = 1,37) и по первому коэффициенту автокорреляции при критическом значении r1 = 0,32;
- нормальности распределения остаточной компоненты по R/S-критерию с критическими значениями от 3 до 4,21.
4) Построить точечный прогноз на 4 шага вперед, т.е. на 1 год.
5) Отразить на графике фактические, расчетные и прогнозные данные.
Таблица 1
Поквартальные данные о кредитах от коммерческого банка на жилищное строительство (в условных единицах) за 4 года
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 2 | 13 | 14 | 15 | 16 |
| Y(t) | 28 | 36 | 43 | 28 | 31 | 40 | 49 | 30 | 34 | 44 | 52 | 33 | 39 | 48 | 58 | 36 |
Решение
Будем считать, что зависимость между компонентами тренд-сезонный временный ряд мультипликативная. Мультипликативная модель Хольта-Уинтерса с линейным ростом имеет следующий вид:
![]() , (1)
, (1)
где k – период упреждения;
Yр(t) — расчетное значение экономического показателя для t-гo периода;
a(t), (t) и F(t) - коэффициенты модели; они адаптируются, уточняются по мере перехода от членов ряда с номером t-1 к t;
F(t+k-L) - значение коэффициента сезонности того периода, для которого рассчитывается экономический показатель;
L - период сезонности (для квартальных данных L=4, для месячных – L=12).
Таким образом, если по формуле 1 рассчитывается значение экономического показателя, например за второй квартал, то F(t+k-L) как раз будет коэффициентом сезонности второго квартала предыдущего года.
Уточнение (адаптация к новому значению параметра времени t) коэффициентов модели производится с помощью формул:
![]() ; (2)
; (2)
![]() ; (3)
; (3)
![]() . (4)
. (4)
Параметры сглаживания a1, a2 и a3 подбирают путем перебора с таким расчетом, чтобы расчетные данные наилучшим образом соответствовали фактическим (т.е. чтобы обеспечить удовлетворительную адекватность и точность модели).
Из формул 1 - 4 видно, что для расчета а(1) и (1) необходимо оценить значения этих коэффициентов для предыдущего период времени (т.е. для t=1-1=0). Значения а(0) и (0) имеют смысл этих же коэффициентов для четвертого квартала года, предшествующего первому году, для которого имеются данные в табл. 1.
Для оценки начальных значений а(0) и (0) применим линейную модель к первым 8 значениям Y(t) из табл. 1. Линейная модель имеет вид:
![]() . (5)
. (5)
Метод наименьших квадратов дает возможность определить коэффициенты линейного уравнения а(0) и (0) по формулам 6 - 9:
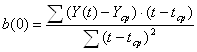 ; (6)
; (6)
![]() ; (7)
; (7)
![]() ; (8)
; (8)
![]() . (9)
. (9)
Применяя линейную модель к первым 8 значениям ряда из таблицы 1 (т.е. к данным за первые 2 года), находим значения а(0) и (0). Составим вспомогательную таблицу для определения параметров линейной модели:
Таблица 2
| t | Y(t) | t-tcp | Y-Ycp | (t-tcp)2 | (Y-Ycp)(t-tcp) | |
| 1 | 28 | -3,5 | -7,625 | 12,25 | 26,6875 | |
| 2 | 36 | -2,5 | 0,375 | 6,25 | -0,9375 | |
| 3 | 43 | -1,5 | 7,375 | 2,25 | -11,0625 | |
| 4 | 28 | -0,5 | -7,625 | 0,25 | 3,8125 | |
| 5 | 31 | 0,5 | -4,625 | 0,25 | -2,3125 | |
| 6 | 40 | 1,5 | 4,375 | 2,25 | 6,5625 | |
| 7 | 49 | 2,5 | 13,375 | 6,25 | 33,4375 | |
| 8 | 30 | 3,5 | -5,625 | 12,25 | -19,6875 | |
| S | 36 | 285 | 0 | 0 | 42 | 36,5 |
Подобные работы: