Критерии оптимальности в эколого-математических моделях

1 Критерии оптимальности в эколого-математических моделях

1.1 Использование принципа выживания

В качестве критерия оптимальности предлагается использовать принцип выживания, полагая, что в диаде выживание – приспособленность первичным является выживание. Пусть динамику экосистемы, в которую входит рассматриваемый вид, адекватно описывает система уравнений с неизвестными численностями особей всех элементов экосистемы. В качестве параметров уравнений выступают экологические условия, а также структурно-функциональные параметры особей всех элементов экосистемы. Выделяют -я популяция и некоторый структурный или функциональный параметр  этой популяции. Делают предположение о том, что популяция состоит из двух подпопуляций, различающихся величиной фенотипического параметра. Пусть x_s⁽¹⁾, x_s⁽²⁾, , – численности и величины фенотипического параметра двух подпопуляций.

Исследование динамической системы, в которую внесены соответствующие изменения, учитывающие различия фенотипического параметра у особей -ой популяции, позволяет анализировать асимптотические свойства численностей подпопуляций. Один из возможных вариантов поведения – вытеснение второй подпопуляции первой (фенотипический параметр имеет селективное преимущество по сравнению с параметром в заданных экологических условиях). Математически этот вариант описывается выражениями

Оптимальной с точки зрения выживания величиной фенотипического параметра является такая величина, при которой для любого отличного от этого значения параметра выполняются условия

Следует отметить, что эти условия верны при произвольных начальных условиях. С оптимальной величиной, удовлетворяющей критерию, следует сопоставлять среднее значение фенотипического параметра.

Также весьма важно то, что если популяция не обладает оптимальным значением параметра, то это не значит, что она элиминируется из биоценоза. Однородная популяция может стабильно существовать при любом значении структурно-функционального параметра , относящимся к области, соответствующей условию стабильного существования популяции, в частности и при значении, не равном оптимальному. Оптимальное же значение устанавливается в результате конкуренции особей с различными значениями рассматриваемого структурно-фенотипического параметра. Именно вследствие этой конкуренции особи с неоптимальными значениями параметра элиминируются.

Применение общего критерия оптимальности возможно путем численного интегрирования уравнений динамики экосистемы при различных величинах рассматриваемого фенотипического параметра. Также возможно применение частных критериев оптимальности, справедливых в конкретных случаях и следующих из общего критерия. Используя критерий отбора, необходимо учитывать ограничения, вытекающие из физико-химических или биологических закономерностей процесса.

1.2 Использование максимума относительной скорости роста численности популяций

В ряде исследований в качестве критерия оптимальности выступало требование максимума относительной скорости роста численности популяции:

Этот критерий может быть применен для определения оптимальных величин структурно-функциональных параметров, если относительная скорость роста численности представлена в виде функции этих параметров. Причем, если рассматриваемый параметр не зависит от возраста особи, то задача нахождения оптимального значения сводится к отысканию параметра, соответствующего максимуму относительной скорости роста; если же рассматриваемый параметр зависит от возраста, то искомая оптимальная зависимость может быть определена путем решения соответствующей вариационной задачи.

Общий критерий оптимальности применяли к исследованию популяций лосей в лесном биоценозе. Оптимизируемыми параметрами были начальный вес новорожденных и рождаемость. Кроме того, из общего критерия оптимальности выводили требование максимума относительной скорости роста популяции, а затем на основании этого требования оптимизировали функцию роста, определяющая зависимость веса тела особи от возраста. Сравнение теоретических величин, полученных для лосей, и соответствующих биологических данных свидетельствовали об их хорошем согласии.

В теории оптимальных биологических процессов применимы более простые критерии, например, определяющие оптимальность структурно-функциональных параметров органов и систем, роль которых в организме сводится к выполнению определенных функций. Критерием оптимальности такого органа является условие минимума его потребностей при условии выполнения этим органом заданных функций

где П_ор – потребности органа; П_п – потребление пищи в единицу времени, связанное с поддержанием жизненного органа, не несущего функциональную нагрузку; П_f – потребление пищи в единицу времени, связанное с осуществлением органом его функций в организме. Использование данного критерия  требует учитывать условия, определяющие функции, выполняемые органом или системой.

Критерий, определяющий оптимальные функциональные параметры, имеет вид: П_f= min. Здесь необходимо сформулировать дополнительные условия, определяющие функции органа.

Если определяющей является энергетическая деятельность органа, то критерий оптимальности может быть сформулирован в виде

,

где W_i – мощность, потребляемая i-м органом.

В экспериментальных условиях было представлено применение общего критерия отбора для определения оптимального в эволюционном смысле начального веса новорожденных (на примере данных биологических исследований для популяции лосей); энергетического критерия оптимальности  для определения функционального состояния системы транспорта кислорода при физической нагрузке и при ее отсутствии, а так же для нахождения энергетически оптимальной концентрации эритроцитов в крови, парциального давления в артериальной и венозной крови, определения оптимальных функциональных параметров системы внешнего дыхания и др.

2 Принцип минимального воздействия в эколого-математических моделях

Один из способов применения целевой функции состоит в формулировании общего утверждения относительно поведения системы. Хорошо известные экстремальные принципы относятся к этому случаю. Самый известный из них – принцип Гамильтона, согласно которому, каждая механическая система ведет себя так, чтобы действие (интеграл по времени от функции Лагранжа) было минимальным. В экологии предпринимались попытки использования этого подхода для получения уравнения роста популяции, точнее, рассматривалась обратная задача: записать действие, которое приведет к специальному уравнению роста. Одна из наиболее удачных попыток разрешить эту задачу, предложенная М.Гатто с соавторами, представлена в работе Дж.Вебба.

В качестве функционала действия, который приведет к логистическому уравнению роста популяции численности , было рассмотрено следующее выражение

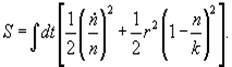
Для упрощения вычисления была сделана замена переменных

Согласно вариационному принципу, уравнение эволюции x(t) задается требованием экстремальности действия, т.е. dS = 0. После необходимых вычислений было получено динамическое уравнение

Чтобы сравнить этот результат с логистическим уравнением                   

его переписали в переменных

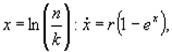
и продифференцировали:

Полученное совпадение показывает, что любое решение логистического уравнения является решением динамического уравнения, выведенного из функционала действия. Однако, не любое решение уравнения  является решением логистического уравнения. Для выявления взаимосвязи между данными уравнениями было проведено исследование полученного уравнения эволюции. После некоторых преобразований и интегрирования было получено выражение

Уравнение эволюции характеризуется константой R: при R > 0 популяция неограниченно растет, при R < 0 популяция достигает максимального значения, а затем уменьшается до 0. Значение R = 0 приводит к логистическому уравнению, тем самым, показывая, что логистический рост – это особый случай равновесия между неограниченным ростом и затуханием.

В работе также был рассмотрен вопрос об интерпретации введенного таким образом “биологического” действия. Описание в терминах кинетической и потенциальной энергии неприемлемо, поскольку ведет к неизменности общей энергии системы (экологические системы обычно подразумеваются открытыми). По аналогии с физикой, где действие разделено на свободное движение и взаимодействие, предлагалось рассматривать действие  как сумму члена, описывающего популяцию, которая не подвержена помехам в росте, и члена V(x), описывающего внешнее влияние среды на популяцию. Однако, подобная интерпретация хорошо описывает лишь случай V(x) = 0, когда применение вариационного принципа приводит к уравнению экспоненциального роста. Сам М.Гатто и его соавторы описывали действие как цену роста.

По мнению Дж.Вебба, применение вариационного принципа позволяет сместить акцент с поведения системы на факторы, которые его определяют, а также делает возможным разделение внутреннего поведения популяции и эффектов внешней среды.

3 Модели случайных стационарных процессов и принципы, на которых они основываются

Модели случайных стационарных процессов рассматривают систему как совокупность взаимодействующих элементов со случайными свойствами. В модель вводиться функция распределения показателей состояния и глобальная характеристика взаимодействия компонентов (энтропия, энергия или вещественый результат). Область применения рассматриваемых моделей ограничивается описанием неструктурированных гомогенных систем, когда необходимо оценить воздействие многих факторов на результирующий признак

Статистические модели строятся при допущении, что исследуемый процесс случаен и может быть изучен с помощью статистических методов анализа систем. Они включают: эмпирические- и динамические статистические модели, корреляционный и факторный анализ, многомерное шкалирование, анализ временных рядов. Для снижения размерности статистических моделей используется ряд методов, например выделение главных компонент в регрессионных уравнениях и гармонических рядах.

3.1 Эргодичность стационарного случайного процесса

Для некоторых процессов вдостаточно длинных реализациях случайного процесса содержатся все его значения. Следователь­но, помимо статистических средних характеристик процесса, определяемых пу­тем усреднения по ансамблю возможных значений процесса, имеется возможность определить временные средние харак­теристики путем усреднения по времени до­статочно длинной реализации процесса.

Случайные процессы, у которых стати­стические и временные средние характери­стики совпадают, называются э р г о д и ч е с к и м и. Далеко не все случайные про­цессы удовлетворяют условию эргодично­сти. Однако многие стационарные процессы этому условию удовлетворяют и для них (несмотря на флюктуации временных сред­них характеристик от одной реализации к другой) с вероятностью, равной единице, временные средние совпадают со статисти­ческими средними:

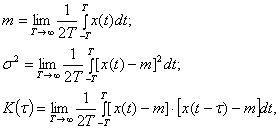
где - реализации процесса, сдвинутые на .

Можно показать (теорема Винера – Хинчина), что функция корреляции стационарного случайного процесса является Фурье-преобразованием некоторой функции частоты :

()

Физический смысл следует из условия , при котором - средняя мощность процесса, а следовательно - его спектральная плотность мощности (спектр мощности).

Иначе говоря, функция корреляции со­держит полную информацию о распределе­нии энергии процесса по частоте, но не мо­жет дать сведений о частотном распределе­нии амплитуд и фаз спектральных состав­ляющих реализаций процесса.

Многие распространенные случайные процессы приближенно можно описать кор­реляционной функцией вида

и соответствующей ей спектральной плот­ностью

.

Итак, спектр мощности и функция кор­реляции не являются независимыми харак­теристиками случайного процесса. Обе эти характеристики определяют степень вероят­ностной связи между значениями сигнала в различные моменты времени или, как ино­гда говорят, степень последейст­вия процесса. Процесс считается не имею­щим последствия, если вероятность наступ­ления последующих значений процесса не зависит от того, какими были предыдущие значения. В процессах с последействием, на­оборот, предыдущее значение процесса влия­ет на вероятность наступления последу­ющего или ряда последующих значений процесса. Чем сильнее выражено последей­ствие процесса, тем больше максимальный интервал времени , в течение которого данное значение процесса еще влияет на следующие за ним значения.

Функция корреляции характеризует сте­пень влияния одного значения процесса на последующие в зависимости от интервала времени , разделяющего эти значения. Как правило, функция корреляции уменьшается с ростом .

Интервал , на котором функция корреляции имеет еще заметную величину, называется интервалом корреляции. Чем больше интервал корреляции, тем более удаленные значения процесса имеют еще вероятностные взаимосвязи.

Аналогично этому за ширину спектра мощности принимают интервал частот для которого значения име­ют еще заметную величину.

Можно показать, что интервал корреля­ции и ширина спектра мощности связаны обратной зависимостью:

где - постоянная величина ( база сигнала).

Так как наиболее полным описанием случайной последовательности является функция распределения вероятностей ее значений, то задача тестирования в общем случае сводится к получению эмпирических вероятностных характеристик по доступным выборочным данным и проверке гипотез об их соответствии некоторым стандартным характеристикам, определяющим различные классы случайных последовательностей и отдельные их свойства. Часто в качестве стандартной случайной последовательности (СП) выступает стандартная случайная последовательность, например, с нормальным распределением и числовыми характеристиками: - математическое ожидание и - дисперсия случайной последовательности.

Общий алгоритм тестирования случайной последовательности с учетом вводимой стандартной случайной последовательности может включать следующие этапы.

1. Определение эмпирических вероятностных характеристик тестируемой случайной последовательности (математического ожидания, дисперсии, корреляционного момента, вероятностей событий и функции распределения вероятностей). Важно, чтобы качество полученных эмпирических оценок соответствовало выдвигаемым априорно требованиям к допустимому отклонению от истинных значений характеристик (доверительному интервалу и доверительной вероятности), а также определялось требуемым для этого размером выборки. На основе полученных характеристик могут быть установлены свойства симметрии распределения (совпадение значений среднего, моды и медианы, либо равенство значений вероятностей превышения и не превышения среднего значения) и близости его формы к некоторому стандартному, например, к нормальному.

2. Построение гистограммы вероятностей и восстановление эмпирического распределения случайной последовательности на основе полученных вероятностных характеристик и выдвижение гипотезы о виде распределения СП.

3. Проверка верности выдвинутой гипотезы по критериям соответствия (согласия) эмпирических и аналитических вероятностных характеристик, а также определение класса и основных свойств случайной последовательности с оценкой показателей качества оценок и решений.

Рассмотрим основные этапы тестирования случайных последовательностей в предположении выполнения условий стационарности и эргодичности выборочных данных.

Вероятностной характеристикой случайной величины ,определяемой непосредственно путем эксперимента, является некоторое число - математическое ожидание, дисперсия, вероятность события . Символ означает истинное значение характеристики. Путем обработки результатов экспериментального исследования X получают экспериментальное значение характеристики, статистическую характеристику или оценку характеристики .

Экспериментальное исследование случайной величины Xс целью определения - оценки (приближенного значения) , заключается в проведении N опытов (испытаний, наблюдений) и получении (путем соответствующих измерений) ряда значений— реализаций X. В результате обработки экспериментальных данных определяется как функция эксперимента.

Если провести еще одну серию из N опытов, то будет получен ряд других реализаций случайной величины Xи другое значение оценки искомой характеристики . Значение случайной величины X,полученное в результате - ого опыта в серии, можно рассматривать как значение случайной величины а оценку - как реализацию более общей случайной величины

, (1)

являющейся функцией независимых случайных величин,все вероятностные характеристики которых совпадают с характеристиками X.

Вероятностными характеристиками системы двух случайных величин (X,Y),определяемыми непосредственно на основании эксперимента, являются математические ожидания, дисперсии, корреляционный момент, вероятность события . Эксперимент заключается в проведении N опытов и получении ряда значений реализаций случайных величин X,Y. В результате обработки экспериментальных данных получается оценка

,

как реализация случайной функции

,                               (2)

аналогичной (1).

Погрешность приближения оценки равная

,                                                     (3)

является, как и , случайной величиной.

Функцию желательно выбирать так, чтобы выполнялось три условия

1. Математическое ожидание равно нулю:

                                                     (4)

2. Дисперсия стремится к нулю с увеличением N

                                                     (5)

3 Дисперсия при данной должна быть наименьшей.

При выполнении условия (4) оценка называется несмещенной, условий (4), (5) - состоятельной, всех трех условий - эффективной.

Вследствие случайного характера погрешности (3) для характе­ристики точности приближенного равенства необходимо располагать вероятностью р_дтого, что абсолютное значение погрешности не превзойдет некоторого предела

                                                (6)

Интервал от до ,в котором с вероятностью р_днаходится истинное значение , называется доверительным интервалом, его границы - доверительными границами, авероятность р_д- доверительной вероятностью.

Если число экспериментальных данных N достаточно велико, то

погрешность (3) состоятельной оценки можно практически счи­тать

распределенной нормально с математическим ожиданием (4), дисперсией и средним квадратическим отклонением При этом выражение (6) имеет вид:

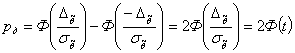
                       (7)

где - функция Лапласа, .

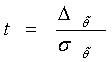С помощью этой формулы решается задача определения доверительной вероятности р_дпо известным данным .

Функция Лапласа выражает зависимость от .Обратная выражает зависимость от . При , имеем

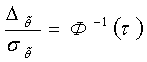                                          (8)

С помощью формулы (8) и обратной функции Лапласа решается задача определения доверительного интервала 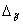по известным р_ди 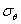и необходимого числа испытаний по известным р_ди .

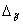При решении первой задачи согласно (8) определяется .При решении второй задачи согласно (8) определяется , а затем N.

Для проведения тестирования СП обычно приводят к стандартному виду. Для случая двоичной ноль - единичной последовательности это достигается перекодировкой исходной последовательности в симметричную -1,1- ю последовательность в соответствии с правилом

.

Здесь - элементы стандартной и исходной последовательностей соответственно.

3.2Определение математического ожидания

Оценка математического ожидания как экспериментальное (выборочное) значение первого начального момента случайной величины X равна

,

В тоже время оценка среднего всей генеральной совокупности значений случайной величины определяется из выражения

,                                                (9)

где - независимые случайные величины с одинаковыми, т.е. с числовыми характеристиками, равными истинным, но неизвестным априори, их значениям.

Математическое ожидание погрешности оценки среднего равно

.           (10)

Дисперсия погрешности оценки среднего равна

. (11)

Среднее квадратическое отклонение оценки математического ожидания

.                                        (12)

Как видно из (10,11) оценка (9) – несмещенная, состоятельная и эффективная.

Выражения (8-12) могут быть положены в основу определения требуемого размера выборки для обеспечения заданных значений доверительного интервала погрешности и доверительной вероятности. Так, имея требования к величине доверительного интервала 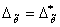и доверительной вероятности и принимая гипотезу о гауссовом характере распределения погрешности оценивания 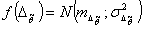, т.е. возможности определения доверительной вероятности в виде 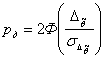, из выражения (8) определяем требуемое значение среднего квадратического отклонения погрешности оценки 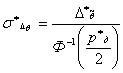. Вместе с тем из выражения (12) следует, что среднее квадратическое значение погрешности оценки среднего случайной величины связано со значениями СКО 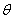и объемом выборки N следующей зависимостью:

,

откуда, приравнивая правые части последних равенств, окончательно определяем выражение для расчета требуемого объема выборки

.

Здесь значение СКО случайной величины может задаваться априорно, либо определяться экспериментально по выборке меньшего чем N объема.

Определение оценки дисперсии и ее среднего квадратического отклонения

Оценка дисперсии как экспериментальное значение второго центрального момента случайной величины Xможет быть вычислена по формуле

.

Так как значение априори неизвестно, то принимают и тогда

.                                          (13)

Математическое ожидание погрешности оценки равно

,                                          (14)

что означает, что оценка (14) является смещенной.

Смещение пропорционально D_xи обратно пропорционально N. Это означает, что оценка D_x,полученная согласно (14), - состоятельная.

Смещение устраняется с переходом к .

При этом вместо (13) имеем

.                             (15)

При больших значениях N результаты расчета по формулам (13) и (15) практически будут одинаковыми.

Выражение для дисперсии оценки (15), равной дисперсии погрешности , при нормальном виде закона распределения X (для худшего случая) можно получить следующее (1-3):

.                                                   (16)

Зависимость среднего квадратического отклонения от его точного значения определяется выражением

.

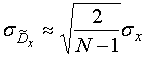3.3Определение корреляционного момента и коэффициента корреляции

Экспериментальное значение корреляционного момента R_xy как оценка смешанного центрального момента m₁₁ системы двух случайных величин равно

Так как значения М_х, М_у неизвестны, то принимают , и тогда

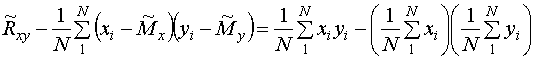
ИЛИ

.                                            (17)

Погрешность оценки

                                                                  (18)

Математическое ожидание погрешности (18)

Это означает, что оценка (17) - смещена и равна

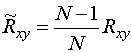.                                                                                       (19)

Можно показать, что она является и состоятельной.

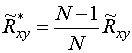Смещение устраняется с переходом от к . При

этом вместо (17) имеем

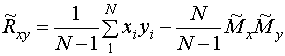. (20)

Для дисперсии оценки (17), равной дисперсии погрешности (18), можно получить (1-3)

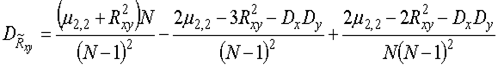,      (21)

где - четвертый смешанный центральный момент системы (XY). При Y = Xвыражения (20) и (21) превращаются в (15), (16). Если система (XY) распределена нормально, то и согласно (21)

Так как значения R_xy, D_x, D_yнеизвестны, то практически используется приближение

.                                                   (22)

Среднее квадратическое значение погрешности (18) равно среднему квадратическому отклонению оценки (20):

. (23)

Оценка коэффициента корреляции определяется согласно

. (24)
Если оценки , получены в результате одной серии наблюдений, а оценка – врезультате другой, то их погрешности , – независимые случайные величины, являющиеся аргументами линейной функции:

.                                                              (25)

Значение рассчитывается согласно (15), доверительный интервал – по формуле (8).

3.4 Определение вероятности события

Экспериментальное значение вероятности Р некоторого события - это частость (1-3)

,                                                                          (26)

причем число п появлений события в серии из N испытаний можно рассматривать как сумму N независимых случайных слагаемых:

,                                                                                            (27)

каждое из которых может принимать только два значения 1 и 0 с вероятностями P и 1 – P.

Математическое ожидание и дисперсия случайной величины X_i:

.                                                              (28)

Погрешность оценки (26) равна

. (29)
Математическое ожидание погрешности и ее дисперсия:

.                                   (30)

Таким образом, оценка (26) - несмещенная и состоятельная. Среднее квадратическое отклонение оценки (26)

.

На практике принимают

.                                                       (31)

3.5 Определение законов распределения случайной величины

Экспериментальное определение законов распределения случайных величин сводится к определению оценок вероятностей, математических ожиданий, дисперсий и средних квадратических отклонений (1-3).

Если случайная величина X - дискретная, то определяются , и оценки значений функции вероятности или оценки значений функции распределения .

Если случайная величина X - непрерывная, то определяются М_х , D_х и оценки f_x(x),F_x(x) плотности вероятности f_x(x) и функции распределения F_x(x).

При оценивании законов распределения непрерывной случайной величины процесс обработки экспериментальных данных - реализаций х ,...,x_N,, начинается с выбора границ а и > а интервала, заключающего возможные значения X, и деления этого интервала на kравных элементарных промежутков с = (b - a)/ k.

При расчете с значения а и следует для удобства округлять,

принимая, например, вместо b = 3,341, а = -2,63 значения 3,4 и -2,7. Во всех случаях округление производится в сторону увеличения разности b- а. Значение kвыбирается в пределах от 8 до 20. Удобно принять k= 10.

После этого определяют границы всех элементарных промежутков и составляют таблицу (табл.1), в которой х'₀=а, x'_k=.Значение - это число реализаций X,оказавшихся в пределах j-ого интерва­ла от , до . Значения и :

    (32)
.                                                                                                                   (33)

При группировке реализаций Xпо отдельным интервалам может оказаться что некоторые из них придутся точно на границу двух смежных промежутков. В этих случаях необходимо прибавить к чис­лам и смежных интервалов по 1/2.

Таблица 1

…