Сравнительный анализ методов оптимизации
Оптимизация как раздел математики существует достаточно давно. Оптимизация - это выбор, т.е. то, чем постоянно приходится заниматься в повседневной жизни. Хотя конечной целью оптимизации является отыскание наилучшего или "оптимального" решения, обычно приходится довольствоваться улучшением известных решений, а не доведением их до совершенства. По этому под оптимизацией понимают скорее стремление к совершенству, которое, возможно, и не будет достигнуто.
Формулировка математической задачи оптимизации.
В достаточно общем виде математическую задачу оптимизации можно сформулировать следующим образом:
Минимизировать (максимизировать) целевую функцию с учетом ограничений на управляемые переменные.
Под минимизацией (максимизацией) функции n переменных f(x)=f(x1, ... ,xn) на заданном множестве U n-мерного векторного пространства En понимается определение хотя бы одной из точек минимума (максимума) этой функции на множестве U, а также, если это необходимо, и минимального (максимального) на U значения f(x).
При записи математических задач оптимизации в общем виде обычно используется следующая символика:
f(x) -> min (max),
x принадлежит U,
где f(x) - целевая функция, а U - допустимое множество, заданное ограничениями на управляемые переменные.
Постановка задачи
Целью данного курсового проекта является изучение методов оптимизации функции. Методов одномерной оптимизации: метод дихотомии, золотого сечения; многомерной безусловной оптимизации: покоординатный циклический спуск, метод Хука – Дживса, правильный симплекс, деформированный симплекс, а также методов условной оптимизации Метод преобразования целевой функции, метод штрафных функций, табличный симплекс – метод.
1. Прямые методы одномерной оптимизации
Задачи одномерной минимизации представляют собой простейшую математическую модель оптимизации, в которой целевая функция зависит от одной переменной, а допустимым множеством является отрезок вещественной оси:
f(x) -> min ,
x принадлежит (a, b).
Максимизация целевой функции эквивалента минимизации ( f(x) -> max ) эквивалентна минимизации противоположной величины ( -f(x) -> min ), поэтому, не умаляя общности можно рассматривать только задачи минимизации.
К математическим задачам одномерной минимизации приводят прикладные задачи оптимизации с одной управляемой переменной. Кроме того, необходимость в минимизации функций одной переменной возникает при реализации некоторых методов решения более сложных задач оптимизации.
Для решения задачи минимизации функции f(x) на отрезке (a, b) на практике, как правило, применяют приближенные методы. Они позволяют найти решения этой задачи с необходимой точностью в результате определения конечного числа значений функции f(x) и ее производных в некоторых точках отрезка (a, b). Методы, использующие только значения функции и не требующие вычисления ее производных, называются прямыми методами минимизации.
Большим достоинством прямых методов является то, что от целевой функции не требуется дифференцируемости и, более того, она может быть не задана в аналитическом виде. Единственное, на чем основаны алгоритмы прямых методов минимизации, это возможность определения значений f(x) в заданных точках.
Рассмотрим наиболее распространенные на практике прямые методы поиска точки минимума. Самым слабым требованием на функцию f(x), позволяющим использовать эти методы, является ее унимодальность. Поэтому далее будем считать функцию f(x) унимодальной на отрезке (a, b).
Функция f(x) называется унимодальной на отрезке (a,b), если она непрерывна на (a,b) и существуют числа ![]() ,
, ![]() , такие, что:
, такие, что:
если ![]() , то на отрезке (a;
, то на отрезке (a; ![]() ) функция f(x) монотонно убывает;
) функция f(x) монотонно убывает;
если ![]() , то на отрезке (
, то на отрезке (![]() ; b) функция f(x) монотонно возрастает;
; b) функция f(x) монотонно возрастает;
при ![]()
Для изучения прямых методов одномерной оптимизации была дана функция:
F(x)=8*cos(5*x)+![]() → min
→ min
a=2.7 b=3.9
И выбрано приближение ε=0,01, ![]() =0,02
=0,02
1.1 Метод дихотомии
В этом методе точки x1 и х2 располагаются близко к середине очередного отрезка (а; b), т.е:
![]() , (2.11)
, (2.11)
где d > 0 – малое число. При этом отношение длин нового и исходного отрезков

близко к 1/2, этим и объясняется название метода.
Отметим, что для любых точек x1 и х2 величина t > 1/2, поэтому указанный выбор пробных точек объясняется стремлением обеспечить максимально возможное относительное уменьшение отрезка на каждой итерации поиска х*.
В конце вычислений по методу дихотомии в качестве приближенного значения х* берут середину последнего из найденных отрезков (а; b), убедившись предварительно, что достигнуто неравенство
![]() .
.
Опишем алгоритм метода деления отрезка пополам.
Шаг 1. Определить x1 и х2 по формулам (2.11). Вычислить f (x1) и f (x2).
Шаг 2. Сравнить f (x1) и f (x2). Если ![]() , то перейти к отрезку (а; x2), положив b = x2 , иначе – к отрезку (x1; b), положив а = x1 .
, то перейти к отрезку (а; x2), положив b = x2 , иначе – к отрезку (x1; b), положив а = x1 .
Шаг 3. Найти достигнутую точность
![]()
Если ![]() , то перейти к следующей итерации, вернувшись к шагу 1. Если
, то перейти к следующей итерации, вернувшись к шагу 1. Если ![]() , то завершить поиск х*, перейдя к шагу 4.
, то завершить поиск х*, перейдя к шагу 4.
Шаг 4. Положить
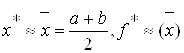 .
.
Замечания:
1. Число d из (2.11) выбирают на интервале (0;2e) с учетом следующих соображений:
а) чем меньше d, тем больше относительное уменьшение длины отрезка на каждой итерации, т.е. при уменьшении d достигается более высокая скорость сходимости метода дихотомии;
б) при чрезмерно малом d сравнение значений f (x) в точках x1 и х2 , отличающихся на величину d, становится затруднительным. Поэтому выбор d должен быть согласован с точностью определения f (x) и с количеством верных десятичных знаков при задании аргумента х.
В таблице 1 приведено решение задания по варианту.
Таблица 1 - Метод дихотомии
| № шага | x1 | x2 | F(x1) | F(x2) | а | b |
|
| 1 | 3.29 | 3.31 | --3.3662671 | -3.3081836 | 2.7 | 3.9 | 0.6 |
| 2 | 2.995 | 3.0015 | -3.9477432 | -3.9985552 | 2.7 | 3.301 | 0.3 |
| 3 | 3.1425 | 3.1525 | -5.7966545 | -5.7920936 | 2.995 | 3.301 | 0.15075 |
| 4 | 2.9995 | 3.15125 | -5.3956845 | -5.4206115 | 3.06875 | 3.1625 | 0.04687 |
| 5 | 3.1118125 | 3.1138125 | -5.7344664 | -5.7448499 | 3.074375 | 3.15125 | 0.03844 |
| 6 | 3.1305312 | 3.1325312 | -5.8005444 | -5.8034734 | 3.1118125 | 3.15125 | 0.01972 |
| 7 | 3.1398906 | 3.1418906 | -5.8073633 | -5.8065477 | 3.1305312 | 3.15125 | 0.01036 |
| 8 | 3.1352109 | 3.1372109 | -5.8061441 | -5.8072013 | 3.1305312 | 3.1418906 | 5.67969E-3 |
| 9 | 3.1309766 | 3.1509766 | -5.8073015 | -5.8074223 | 3.1352109 | 3.1418906 | 3.33984E-3 |
| 10 | 3.1387207 | 3.1407207 | -5.8074693 | -5.807122 | 3.1375508 | 3.1465703 | 2.16992E-3 |
| 11 | 3.1381357 | 3.1401357 | -5.8074196 | -5.8073064 | 3.1375508 | 3.1407207 | 1.585E-3 |
| 12 | 3.1384282 | 3.1404282 | -5.807453 | -5.8072227 | 3.1381357 | 3.1407207 | 1.292E-3 |
|a-b|=0.001<= ε, x*=(a+b)/2=3.139282, f(x*)=-5.8074527
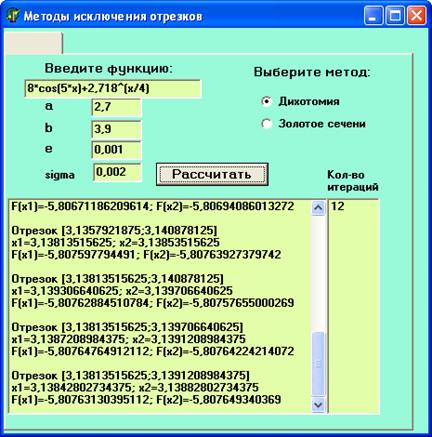
Рисунок 1 – Результат выполнения программы (Метод дихотомии).
1.2 Метод золотого сечения
Метод золотого сечения. Рассмотрим такое симметричное расположение точек x1 и х2 на отрезке (а; b), при котором одна из них становится пробной точкой и на новом отрезке, полученном после исключения части исходного отрезка. Использование таких точек позволяет на каждой итерации метода исключения отрезков, кроме первой, ограничиться определением только одного значения f (x), так как другое значение уже найдено на одной из предыдущих итераций.
Найдем точки x1 и х2 , обладающие указанным свойством.
Рассмотрим сначала отрезок (0; 1) и для определенности предположим, что при его уменьшении исключается правая часть этого отрезка. Пусть х2 = t, тогда симметрично расположенная точка х1 = 1–t (рис. 2.7).
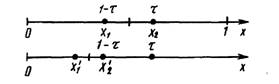
Рис. 2.7. Определение пробных точек в методе золотого сечения
Пробная точка х1 отрезка (0; 1) перейдет в пробную точку х2¢ = 1–t нового отрезка (0; т). Чтобы точки х2 = t, и х2¢ = 1–t делили отрезки (0; 1) и (0; t) в одном и том же отношении, должно выполняться равенство
![]()
или
![]() ,
,
откуда находим положительное значение
![]() …
…
Таким образом,
х1 = 1–t = ![]() ,
, ![]() .
.
Для произвольного отрезка (а; b) выражения для пробных точек примут вид
![]() ;
;
![]()
В таблице 2 приведено решение задания по варианту.
Опишем алгоритм метода золотого сечения.
Шаг 1. Найти х1 и х2 по формулам (2.15). Вычислить f (x1) и f (x2). Положить ![]() ,
,
![]() .
.
Шаг 2. Проверка на окончание поиска: если en > e, то перейти к шагу 3, иначе – к шагу 4.
Шаг 3. Переход к новому отрезку и новым пробным точкам. Если f (x1) £ f (x2) то положить b=x2 , x2=x1 , f (x2) £ f (x1), x1=b–t(b–a) и вычислить f (x1), иначе – положить a=x1, x1= x2 , f (x1) = f (x2), x2=b+t(b–a) и вычислить f (x2). Положить en = ten и перейти к шагу 2.
Шаг 4. Окончание поиска: положить
![]() ,
, ![]() .
.
Результаты вычислений на остальных итерациях представлены в таблице 2 .
Таблица 2 - Метод золотого сечения
| № шага | a | b | x1 | x2 | F(x1) | F(x2) |
|
| 1 | 2.7 | 3.9 | 3.1584 | 3.4416 | -5.7694 | 1.79829 | 0.370820393 |
| 2 | 2.7 | 3.4416 | 2.98329 | 3.1583 | -3.1542 | -5.7698 | 0.229179607 |
| 3 | 2.9833 | 3.4416 | 3.158365 | 3.26652 | -5.76957 | -4.22659 | |
| 4 | 2.98329 | 3.266546 | 3.09148 | 3.15833 | -5.58444 | -5.769704 | |
| 5 | 3.09148 | 3.26652 | 3.15835 | 3.199661 | -5.76962 | -5.43999 | |
| 6 | 3.09148 | 3.19966 | 3.13281 | 3.15834 | -5.8039 | -5.76967 | |
| 7 | 3.09148 | 3.15834 | 3.11702 | 3.132801 | -5.7600 | -580399 | |
| 8 | 3.11702 | 3.15834 | 3.13281 | 3.14256 | -5.8039 | -5.80627 | |
| 9 | 3.13281 | 3.15834 | 3.14256 | 3.14859 | -5.8063 | -5.7982 | |
| 10 | 3.13281 | 3.14859 | 3.1388 | 3.14856 | -5.08076 | -5.8063 | |
| 11 | 3.13281 | 3.14256 | 3.13653 | 3.13883 | -5.8071 | -5.8076 | |
| 12 | 3.13653 | 3.142557 | 3.13883 | 3.140255 | -5.80764 | -5.80745 | |
| 13 |
|a-b|=7.893370498E-3< ε, x*=(a+b)/2=3.1407091
f(x*)=-5.807126299
Сравнив два метода, мы видим, что для данной функции лучше подходит метод дихотомии, т.к. он быстрее приводит к оптимальному решению.
2 Прямые методы безусловной оптимизации многомерной функции
Задача безусловной оптимизации состоит в нахождении минимума или максимума функции в отсутствие каких-либо ограничений. Несмотря на то что большинство практических задач оптимизации содержит ограничения, изучение методов безусловной оптимизации важно с нескольких точек зрения. Многие алгоритмы решения задачи с ограничениями предполагают сведение ее к последовательности задач безусловной оптимизации.
Рассмотрим методы решения минимизации функции нескольких переменных f, которые опираются только на вычисление значений функции f(x), не используют вычисление производных, т.е. прямые методы минимизации. В основном все методы заключаются в следующем. При заданном векторе х определяется допустимое направление d. Затем, отправляясь из точки х, функция f минимизируется вдоль направления d одним из методов одномерной минимизации. Будем предполагать, что точка минимума существует. Однако в реальных задачах это предположение может не выполняться.
Для изучения прямых методов безусловной оптимизации многомерной функции была дана функция:
F(x1,x2)=a*x*y+(b*y+c*x)/x*y → min
a=5 b=3.5 c=2.5
x1= ![]()
x2=![]()
2.1 Метод покоординатного циклического спуска
Суть метода заключается в том, что в начальном базисе закрепляется значение одной координаты, а переменными считаются остальные, и по этой координате производится одномерная оптимизация
![]()
![]() базисная точка переносится в
базисная точка переносится в ![]()
![]() ,
, ![]()
![]() базисная точка переносится в
базисная точка переносится в ![]()
Циклы повторяются до тех пор, пока в ε окрестности найденной базисной точки будет улучшение функции. Решением поставленной задачи является точка ![]() в ε окрестности которой функция не принимает значение, лучшие, чем в этой точке.
в ε окрестности которой функция не принимает значение, лучшие, чем в этой точке.
Для решения поставленной задачи выбрано приближение ε=0,01 α=0,15
Таблица 3 - Метод покоординатного циклического спуска
| № шага | x1 | x2 | Z(x1,x2) | α |
| 0 | 2.1932884 | 1.6094917 | 20.7994602 | Факторіальні кільця та їх застосування Статистическое наблюдение, первоначальная обработка и представление ее данных Численные методы решения типовых математических задач
Актуально:
|