Чисельні методи розв’язування крайових задач для звичайних диференціальних рівнянь

Міністерство освіти і науки України

Сумський Державний Університет

Кафедра Інформатики

Курсова робота

на тему:

«Чисельні методи розв’язування крайових задач для звичайних диференціальних рівнянь»

«Метод скінченних різниць»

Суми 2006

Зміст

Вступ

Постановка задачі

Метод скінчених різниць

Дослідження точності

Збіжність різницевої схеми

Програмна реалізація(представлена на мові Delphi

Висновки

Література

Вступ

На сьогоднішній день існує багато чисельних методів розв’язування крайових задач для звичайних диференціальних рівнянь. Але всі вони поділяються на дві групи: наближені методи чисельного розв’язання і наближені аналітичні методи.

Наближені чисельні методи:

1.Розв'язання лінійної крайової задачі комбінуванням двох задач Коші:

Припустимо, що розв'язок задачі (11.4), (11.5) будемо шукати у вигляді

                                                                          (11.6)

де  - деяка константа,  - функція, що задовольняє однорідне рівняння

                                                                                             (11.7)

а  - функція, яка задовольняє неоднорідне рівняння

                                                                                         (11.8)

Через те, що рівняння (11.4) є лінійним, функція буде його розв'язком для будь-якого . Справді,

Якщо припустити, що розв’язок (11.6) задовольняє першу граничну умову (11.5) для будь-якого , то отримаємо рівняння

Ця гранична умова задовольняється, якщо покласти

                                                                  (11.9)

                                                         (11.10)

Рівність (11.9) справедлива, коли прийняти, наприклад, що

,                                                                 (11.11)

Щоб задовольнити рівність (11.10), можна покласти

, , якщо                                               (11.12)

, , якщо                                               (11.13)

Враховуємо, що одночасно  і  на нуль не перетворюються через умову (11.5).

Таким чином, для розв'язання крайової задачі (11.4), (11.5) необхідно знайти розв'язок задач

, ,                          (11.14)

                                                            (11.15)

з початковими умовами (11.12) чи (11 13). Для цього можна використати будь-який чисельний метод розв'язання задачі Коші для рівнянь другого порядку. Наближений розв'язок цих рівнянь отримуємо на відрізку , у результаті чого стають відомими значення ,,,. Це дозволяє вибрати таку константу . щоб функція (11.6) задовольняла не тільки рівняння (11.12) і першу граничну умову, але і другу граничну умову (11.5). Маємо

,

звідки

,

якщо .                                      (11.16)

Коли , то однорідна крайова задача

, ,

мас нетривіальний розв'язок , який є ознакою виродженості початкової задачі (11.4), (11.5).

2. Метод прицілювання:

Викладений вище метод редукції крайової задачі до задачі Коші має певні недоліки.

Він не дозволяє використовувати методи розв'язання задачі Коші зі змінним порядком і змінним кроком. Розв'язки  і  повинні обчислюватись на сітці з однаковим кроком, інакше знайти їх комбінацію (11.6) буде неможливо.

Використання методу, як правило, обмежується лише одновимірною лінійною задачею. Причина полягає в тому, що під час розв'язання системи рівнянь потрібно обчислювати не одне значення константи А (11.16), а матрицю А, що є далеко не простою задачею.

Метод не придатний для розв'язання нелінійних крайових задач.

Ці недоліки спричинилися до появи нових методів. На практиці двоточкова крайова задача (лінійна чи нелінійна) звичайно розв'язується методом прицілювання (стрільби), назва якого запозичена із теорії артилерійської стрільби. Відповідно до цього методу розв'язок шуканого рівняння другого порядку

із заданими граничними умовами

, ,

знаходять у такий спосіб: ітераційним розв'язанням задачі Коші

                                                                         (11.18)

 і

підбирається значення першої похідної , для якої виконується друга крайова умова .

Спочатку вибирається довільне значення  і розв'язується задача Коші (11.18). Значення  бажано вибирати так, щоб наближений розв'язок на кінці інтервалу задовольняв умову  (рис 1.). Потім вибирається , і розв'язання задачі Коші повторюється. Тепер бажано вибрати його так, щоб виконувалась умова  (рис 1.).

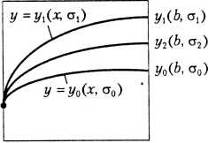
рис. 1. Ілюстрація методу стрільби.

Після цього шляхом інтерполяції уточнюється значення  для задач Коші з початковими умовами:

,

……..                   ……..                   ……..

де  - наближений розв'язок задачі Коші в точці  для вибраного значення .

Метод прицілювання є універсальним і використовується для розв'язання нелінійних диференціальних рівнянь -ого порядку. Слід зазначити, що довільний вибір початкового наближення  може привести до того, що задача (11.18) виявиться жорсткою навіть у випадку, коли задача (11.1), (11.2) є добре обумовленою.

Наближені аналітичні методи:

3.Метод колокацій:

У методі колокацій розв'язок крайової задачі (11.4), (11.5) шукається у вигляді функції

.                                                               (11.36)

де ,  - лінійно незалежні, двічі диференційовані базисні функції, визначені на відрізку. Функція  повинна задовольняти задані граничні умови (11.5):

                                                        (11.37,а)

а функції,  - відповідні однорідні граничні умови, тобто

,

,

.                                                                                (11.37,б)

Через лінійність граничних умов функція  у (11.36) задовольняє граничним умовам (11.24) для будь-яких значень . Наприклад, у точці  маємо

.

Аналогічно для  отримаємо

Суть методу колокацій полягає в тому, що для заданих  точок на відрізку , названих вузлами колокації, підбирають значення  так, щоб отримана при цьому функція  (11.36) задовольняла рівняння (11.4) у кожному з вузлів колокації:

,(11.38)

де

, .

Покладемо

,                                                                            (11.39)

тоді (11.39) матиме стандартний вигляд системи лінійних алгебраїчних рівнянь:

,                                                               (11.40)

відносно коефіцієнтів . Якщо розв'язати цю систему і підставити отримані значення коефіцієнтів у вираз (11.36), отримаємо наближений розв'язок .

Точність розв'язку крайової задачі методом колокацій залежить від типу базисних функцій . У конкретних задачах вибір цих функцій слід здійснювати з урахуванням апріорної інформації про розв'язки задачі або на основі емпіричних даних. Нехай  - це лінійна функція

,                                                                            (11.41)

параметри якої визначимо таким чином, щоб вона задовольняла неоднорідні граничні умови (11.5), тобто з системи рівнянь

,

.                                                                  (11.42)

Функції  можна задати у вигляді:

, .                                       (11.43)

Очевидно, що за будь-яких  функція (11.43) задовольняє умову (11.37, а). Значення , за якого буде задовольнятися друга умова (11.37, б), таке:

.                                                   (11.44)

Якщо в умовах (11.37, а, б) , то можливий інший вибір, а саме:

,

.                                                   (11.45)

4.Метод Гальоркіна

Як і в методі колокацій, у методі Гальоркіна наближений розв'язок крайової задачі (11.4), (11.5) шукаємо у вигляді

                                                                (11.48)

де ,  - лінійно незалежні, двічі диференційовані базисні функції, визначені на відрізку . Функція  повинна задовольняти задані граничні умови (11.37, а), а функції ,  - відповідні однорідні граничні умови (11.37, 6).

Необхідно, щоб система базисних функцій ,  була ортогональною на відрізку , тобто

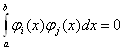 при  і ,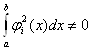

і повною. Остання вимога означає, що не повинно існувати ніякої іншої відмінної від нуля функції, яка ортогональна до всіх функцій , .

Використовуючи наближений розв'язок (11.48) знайдемо нев'язку:

                                                    (11.49)

Коефіцієнти  мають бути такими, щоб значення інтеграла від квадрата нев'язки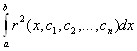

було найменшим.

Це досягається лише в тому випадку, коли нев'язка  ортогональна до всіх базисних функцій . Умову ортогональності запишемо у вигляді:

,

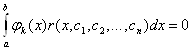або

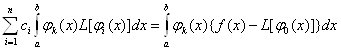,             (11.50)

Таким чином, отримаємо систему лінійних алгебраїчних рівнянь для обчислення коефіцієнтів

5.Метод найменших квадратів

У методі найменших квадратів наближений розв'язок крайової задачі (11.4) і (11.5) задасться у вигляді:

,                                                               (11.54)

де ,  - лінійно незалежні, двічі диференційовані базисні функції, визначені на відрізку . Функція  повинна задовольняти задані граничні умови (11.37, а), а функції ,  - відповідні однорідні граничні умови (11.38, б).

Підставимо наближений розв'язок (11.54) у рівняння (11.4) і знайдемо нев'язку:

,                                                (11.55)

абсолютна величина якої для  повинна бути якомога меншою. Тому вимагатимемо, щоб виконувалася умова

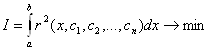                                                      (11.56)

Значення інтегралу будуть мінімальними за умов:

,

,

,

…      …      …      …

.

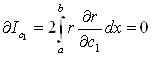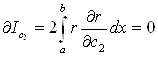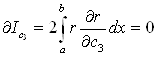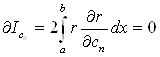На основі цих умов формується система лінійних рівнянь для обчислення коефіцієнтів .

6.Метод скінченних елементів

Метод Гальоркіна накладає певні обмеження на вибір системи базисних функцій, які залежать від граничних умов крайової задачі. Це обмеження значно ускладнює реалізацію методу, особливо під час розв'язання задач математичної фізики. Це обмеження можна подолати, якщо для апроксимації розв'язку використовувати систему простих базисних функцій, які залежать від координат вузлів на відрізку . У цьому випадку розв'язання крайової задачі зводиться до формування і розв'язання системи лінійних алгебраїчних рівнянь, тому метод отримав назву методу скінченних елементів. Його часто використовують для розв'язання дво- та тривимірних диференціальних рівнянь із частинними похідними.

Шукатимемо наближений розв'язок задачі

,                                       (11.59)

як лінійну комбінацію простих однотипних функцій

,                                                                         (11.60)

що мають вигляд

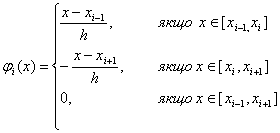                                        (11.61)

і, як правило, називаються фінітними. Графік однієї з таких функцій наведено на рис. 2, де видно, що функція не дорівнює нулю тільки на інтервалі . Щодо множини фінітних функцій, які задаються на відрізку  відомо, що вони лінійно незалежні (більш того, ортогональні в спеціальній енергетичній нормі) і утворюють повну систему в просторі .Це дає підставу використати їх як базисні функції в методі Гальоркіна.

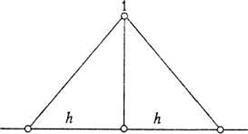
рис. 2. Графік фінітної функції.

Запишемо умову ортогональності (11.50):

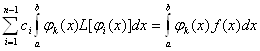,                       (11.62)

і отримаємо систему лінійних алгебраїчних рівнянь для знаходження невідомих .Праві частини цих рівнянь позначимо через  і отримаємо для їх обчислення вираз

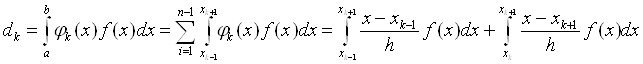(11.63)

Коефіцієнти системи рівнянь (11.62) позначимо через

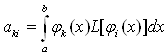
Знайдемо вирази для коефіцієнтів системи рівнянь  з невідомими . Підставляючи в останній вираз , отримаємо

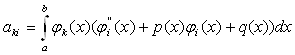
Перший з інтегралів у цьому виразі обчислимо по частинах:

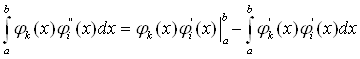
Оскільки за граничних умов (11.60) використовуються , базисних функцій від  до  і всі вони в точках  і  дорівнюють 0, то

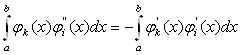
Тоді вираз для обчислення набуває вигляду:

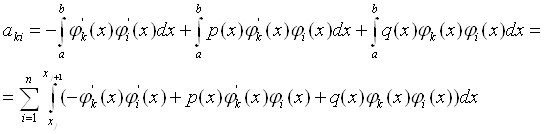(11.64)

Для обчислення  треба знайти значення похідних від фінітних функцій. Із цією метою диференціюємо (11.61) і отримуємо:

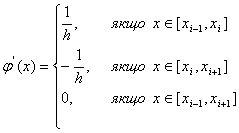                                                (11.65)

Функція відмінна від нуля тільки на інтервалі . Крім того, на одному і тому ж інтервалі ненульовими є дві базисні функції і їх похідні з сусідніми індексами (рис. 3), тобто на інтервалі  відмінні від нуля , , ,  і т. д.

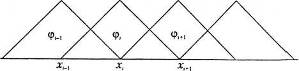
рис. 3. Система фінітних функцій.

У виразі для  (11.64) добутки , ,  можна вважати відмінними від нуля тому, що на елементарному інтервалі не дорівнюють нулю фінітні функції та їх похідні, які мають сусідні індекси у випадках, коли . А це означає, що

 для ,                                                                  (11.66)

тобто матриця системи  (11.62) є тридіагональною матрицею. її ненульові елементи обчислюються таким чином. Формули для діагональних елементів отримаємо, приймаючи  у виразі (11.64):

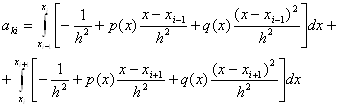                            (11.67)

Для , отримаємо формули для елементів правої бічної діагоналі матриці :

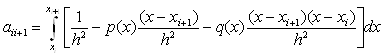,                  (11.68)

а для  - лівої;

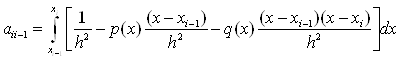
Три останні вирази визначають систему алгебраїчних рівнянь (11.62) для невідомих коефіцієнтів .

Розглянемо розв’язання задачі (11.59) у випадку неоднорідних граничних умов

,                                                   (11.70)

і зведемо її до розв'язання задачі з однорідними граничними умовами. Для цього введемо заміну:

, де .

Двічі диференціюючи цю функцію і підставляючи вирази для похідних у рівняння (11.59), отримаємо крайову задачу з однорідними граничними умовами:

,

, .                                                                      (11.71)

Постановка задачі

Щоб знайти єдиний розв'язок звичайного диференціального рівняння, необхідно задати деякі допоміжні умови, що використовуються для обчислення інтегрування. Для рівняння n-ого порядку потрібно п таких умов. Якщо ці умови задаються для одного значення незалежної змінної (зокрема, для одного кінця інтервалу, на якому необхідно знайти розв'язок), то говорять про початкові умови для задачі Коші. Якщо ж додаткові умови задаються для значень незалежної змінної на різних кінцях інтервалу, то мають на увазі крайову задачу і граничні умови для неї.

Двоточкова крайова задача для рівняння другого порядку має такий вигляд:

                                                      (11.1)

із граничними умовами

                                                                              (11.2)

Перш ніж застосовувати будь-який чисельний метод, варто перевірити умови, що гарантують існування розв'язку цієї задачі. Наведена нижче теорема визначає загальні умови, що забезпечують існування й одиничність розв'язку.

Теорема. Припустимо, що  неперервна в області

І що

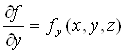 і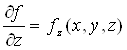

Теж неперервні на. Якщо існує постійна, для якої виконуються умови

для всіх

 для всіх         (11.3)

то крайова задача (11.1) (11.2) має єдиний розв'язок  для .

Найчастіше зустрічаються і найкраще вивчені двоточкові лінійні крайові задачі виду

,                                              (11.4)

,                              (11.5)

де

,

Умови, які повинні задовольняти функції ,  і , для того щоб задача (11.4), (11.5) мала єдиний розв'язок, випливають із теореми як наслідок.

Наслідок. Якщо  і  неперервні на  і , то задача (11.4), (11.5) має єдиний розв'язок на .

Граничні умови (11.5) визначають третю крайову задачу для рівняння (11.4). Якщо припустити, що , то умови (11.5) визначають першу крайову задачу, а коли  - другу.

Точне (аналітичне) розв'язання крайових задач - більш складна процедура, ніж знаходження розв'язку задачі Коші. Це спричинило появу великої кількості наближених методів. Ці методи можна розділити на дві групи: наближено-аналітичні методи, що дають наближений розв'язок крайової задачі на відрізку  у вигляді конкретної аналітичної функції, і чисельні методи, що визначають розвозок у вигляді табличної функції, заданої на сітці відрізка .

Метод скінченних різниць

Ідея методу скінченних різниць полягає в тому, що похідні в диференціальному рівнянні (11.4) і граничних умовах (11.5) заміняються їх скінченними різницями. Для цього спочатку введемо на відрізку  сітку з кроком :

.

Позначимо через точний розв'язок задачі (11.1) у і-му вузлі сітки, а через  - наближений розв'язок у цій точці. Заміняючи в кожному внутрішньому вузлі сітки похідні різницями, отримаємо різницеві рівняння:

,

Симетричні різницеві апроксимації похідних першого і другого порядків мають похибку другого порядку відносно , тобто . Це легко довести на основі розкладання в ряд Тейлора точного розв'язку рівняння. Дійсно, для вузлів та  маємо

з різниці яких отримуємо шуканий результат:

,

                                        (11.21)

Знайдемо нев’язку різницевого рівняння

.

Оскільки  є точним розв'язком рівняння (11.4),

 та .                                           (11.22)

Тому різницеве рівняння (11.21) апроксимує вихідне диференціальне рівняння

(11.4) також із другим порядком відносно .

Тепер апроксимуємо граничні умови скінченними різницями:

,                                    (11.23)

Знайдемо похибку апроксимації граничних умов. Нев’язки граничних умов (11.23) мають вигляд:

, .

Асиметрична апроксимація першої похідної на відміну від симетричної має глобальну похибку першого порядку відносно , тобто . Це безпосередньо випливає з розкладання в ряд Тейлора

,

із якого отримуємо

,

Отже, граничні умови (11.23) апроксимуються з першим порядком за к. Порядок їх апроксимації можна підвищити до другого, наприклад, використовуючи співвідношення

,           (11.24)

похибка апроксимації яких також пропорційна , як і для випадку симетричної апроксимації похідних. Це випливає із порівняння двох рядів Тейлора:

Якщо перший вираз помножити на 4 і відняти його від другого, отримаємо:

.

Після його підстановки у формулу (11.24) знаходимо нев'язку у вигляді:

тобто крайова умова апроксимується з другим порядком відносно .

У такий же спосіб доводиться, що і друга гранична умова (11.23) апроксимується з другим порядком відносно .

Розглянемо ще одну можливість апроксимації крайових умов типу (11.5) на прикладі умови

.

Для цього за межами інтервалу  вводиться додаткова точка , за допомогою якої обчислюється перша похідна за симетричною формулою апроксимації:

.                                                             (11.25)

Точку  можна виключити, скориставшись співвідношенням (11.25) і різницевою апроксимацією диференціального рівняння (11.4) в кінцевій точці інтервалу .

Отримуємо рівняння для граничної умови в точці  із порядком , яким можна замінити останнє рівняння в системі алгебраїчних рівнянь, одержаній у разі кусочно-різницевої апроксимації похідних у рівнянні (11.4).

Те ж саме можна зробити з першою умовою (11.5) і першим апроксимуючим рівнянням для . Варто підкреслити, що врахування граничних умов різних типів впливає тільки на перше й останнє рівняння цієї системи.

Зведемо подібні члени в рівнянні (11.21) і отримаємо стандартне триточкове різницеве рівняння:

,                            (11.27)

.

Включивши до системи рівнянь (11.25) різницеве рівняння (11.23) чи (11.24), отримаємо систему рівнянь, що містить  рівняння з  невідомими .

Порівняємо ці два варіанти апроксимації крайової задачі. У першому з них система лінійних алгебраїчних рівнянь, утворена рівняннями (11.21) і (11.23), має тридіагональну матрицю коефіцієнтів, і її можна розв'язати методом прогону. Щоб застосувати метод прогону в другому випадку, слід створити відповідну тридіагональну матрицю. Для цього потрібно з першого рівняння (11.27) для

Маємо рівняння з двома невідомими -  і . Замінимо ним перше рівняння (11.24). Виконаємо такі ж перетворення з другим (11.24) і останнім рівнянням (11.27) для :

Виключивши з них , знаходимо:

Це рівняння містить дві невідомі -  і . Замінимо ним друге рівняння (11.27). Два останні рівняння разом із (11.27) утворюють систему рівнянь із тридіагональною матрицею, що апроксимує вихідну крайову задачу (11.4), (11.5) з порядком . Цю систему також можна розв'язати методом прогону. Метод прогону є стійким, якщо матриця коефіцієнтів діагонально домінантна. Забезпечити діагональну домінантність можна обранням кроку . Для цього необхідно, щоб для системи рівнянь (11.27) виконувались умови:

 і , .

Підсилюючи останні нерівності, маємо такі обмеження на величину кроку:

 і , .                                   (11.28)

Щоб задовольнялись умови (11.23), мають виконуватись нерівності

 і .                                                                    (11.29)

Наявність обмежень (11.28) і (11.29) свідчить про умовну стійкість розглянутого методу апроксимації.

Дослідження точності

Дослідження точності отриманих виразів при чисельних розрахунках зручно робити за допомогою апостеріорної оцінки, по швидкості спадання членів відповідного ряду Тейлора. Якщо крок сітки досить малий, то похибка близька до першого відкинутого члена.

У такий спосіб порядок точності результату стосовно кроку сітки дорівнює числу залишених членів ряду, чи іншими словами, він дорівнює числу вузлів інтерполяції мінус порядок похідної. тому мінімальне число вузлів необхідне для обчислення m-ої похідної, дорівнює m+1, воно забезпечує перший порядок точності.

Ці висновки відповідають принципу: при почленному диференціюванні ряду швидкість його збіжності зменшується.

Якщо врахувати погіршення збіжності ряду при диференціюванні, то можна зробити висновок: навіть якщо функція задана добре складеною таблицею на досить докладній сітці, то практично чисельним диференціюванням можна визначити першу і другу похідні, а третю і четверту – лише з великою похибкою. Похідні більш високого порядку рідко вдається обчислити з задовільною точністю.

Одним з найбільш простих і досить ефективних методів оцінки похибки й уточнення отриманих результатів є правило Рунге. Для оцінки похибки за правилом Рунге порівнюють наближені розв’язки, отримані при різних кроках сітки. При цьому використовується наступне припущення: глобальна похибка методу порядку у точці х_iподається у вигляді

.

За формулою Рунге

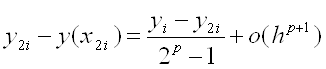
Таким чином, із точністю до (величина більш високого порядку малості) при h→0 похибка методу має вигляд:

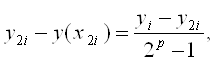
де y_i– наближене значення, отримане в точці з кроком h; y_2i– із кроком h/2; - порядок методу; y(x_2i) - точний розв’язок задачі.

Формула Рунге:

.

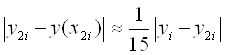Збіжність різницевої схеми

Постановка задачі

Універсальним методом наближеного розв’язання, є метод скінченних різниць. Як задачі представлені у вигляді систем нелінійних рівнянь у часткових, які розглядаються у області

Розв’язок задачі в  має додаткові умови:

1) умови при  називають початковими умовами;

2) умови на границі  області — крайовими або граничними умовами.

Задача з початковими умовами – називається задачею Коші.

Нехай . Тоді для функції  маємо задачу:

                                                                             (1)

                                                                              (2)

де и- диференціальні оператори задачі і крайових умов. Припустимо ,що відповідно задачі (1-2) поставлені коректно, тобто оператори А и R; область D и її границі Г такі, що при виборі відповідних класів функцій і правих частин у рівняннях (1) и (2) розв’язок існує, і залежить від початкових даних.

Різницева схема

Введемо у області  сітку , яка складається з множини внутрішніх вузлів  і множини граничних вузлів :

Далі розглянемо сіткові функції  і з їх допомогою побудуємо наближений розв’язок задачі (1-2). Для цього відносно  сформулюємо "різницеву задачу", заміняючи оператори задачі  і  і їх сітковим аналогами и. Тоді на сітковому шаблоні  маємо

                                                                          (3)

                                                                         (4)

Задачу (3)-(4) назвемо різницевою схемою для задачі (1)-(2). Звичайно це алгебраїчна система рівнянь відносно