Методы отсечения

Среди практически важных задач отыскания условного экстремума линейной функции важное место занимают задачи с требованием целочисленности всех (части) переменных. Они получили название задач целочисленного (частично целочисленного) программирования.

Исторически первой задачей целочисленного типа является опубликованная венгерским математиком Е. Эгервари в 1932 г. задача о назначении персонала.

Существуют различные методы решения таких задач, и заметное место среди них занимают методы отсечения. Рассмотрим в этой работе некоторые из методов отсечения, предварительно более подробно разобравшись с постановкой линейных целочисленных задач.

1. Постановка линейной целочисленной задачи

Среди совокупности п неделимых предметов, каждый i-и (i=1,2,…, п) из которых обладает по i-й характеристике показателем и полезностью найти такой набор, который позволяет максимизировать эффективность использования ресурсов величины .

Математическая модель этой задачи может быть представлена следующим образом:

в области, определенной условиями

(1)

(2)

- целые, . (3)

найти решение при котором максимизируется (минимизируется) значение целевой функции

(4)

Если ,то (1–4) является моделью задачи целочисленного программирования, если - моделью задачи частично целочисленного программирования.

Частным случаем задачи целочисленного программирования является задача с булевыми переменными. Ее математическая модель в общем виде записывается следующим образом:

в области, определенной условиями

(5)

(6)

найти решение , при котором максимизируется (минимизируется) значение функции

(7)

К классу задач целочисленного программирования примыкают задачи, в которых условие целочисленности всех или части переменных заменено требованием дискретности. А именно, для каждой j-и переменной заранее определен набор значений (не обязательно целых), которые она может принимать: где .

Предполагается, что ранжированы, т.е.. Математическая модель общей задачи дискретного программирования может быть представлена следующим образом:

в области, определенной условиями

(8)

(9)

найти решение , при котором максимизируется (минимизируется) линейная функция

(10)

Условие (9) определило название этого класса; задач. Если ,то (8–10) называется задачей дискретного программирования; если , то (8–10) называется задачей частично дискретного программирования.

Нетрудно видеть, что условие (2–3) задачи (1–4) и условие (6) задачи (5–7) являются частным случаем условия (9) задачи (8–10). Действительно, (2–3) соответствует тому случаю, когда для . Условие (9) соответствует случаю, когда .

Для задач целочисленного типа определено понятие допустимого и оптимального решения.

Вектор , удовлетворяющий условиям (1–3) (соответственно (8–9)), называется допустимым решением задачи (1–4) (соответственно (8–10)). Допустимое решение, при котором функция (4) (соответственно (10)) достигает наибольшего (наименьшего) значения, называется оптимальным решением.

Определив понятие допустимого и оптимального решения, естественно поставить вопрос об их нахождении. Казалось бы, что естественный путь решения целочисленной задачи состоит в решении соответствующей линейной задачи с последующим округлением компонент ее оптимального плана до ближайших целых чисел. На самом деле такой путь в большинстве случаев не только уводит, от оптимума, но даже приводит иногда к недопустимому решению задачи.

ПРИМЕР. В области, определенной условиями

– целые

найти максимум функции .

Решим задачу геометрически (рис. 1). Область поиска экстремума – многоугольник ODABC, но так как линия уровня целевой функции параллельна стороне АВ многоугольника, экстремум достигается в вершинах и , а также в любой точке отрезка АВ, и равен 7.

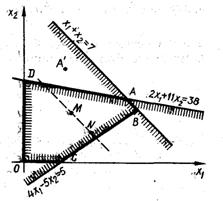
(рис. 1)

Однако нас интересуют лишь точки с целочисленными координатами, следовательно, ни А, ни Вне являются допустимым решением задачи. Округляя значение координат А, получим Но точка А' не принадлежит области поиска. Можно показать, что целочисленный оптимум достигается в точках N (3; 2) и M (2; 3) и равен 5. Обе точки внутри области поиска.

Построенный нами пример показал, что для решения задач с требованием целочисленности необходимо рассмотреть особые методы оптимизации; и, кроме того, мы видим, что оптимальное решение задач целочисленного программирования не обязательно принадлежит границе многогранника (многоугольника) условий, что было характерно для задач линейного программирования.

2. Теоретические основы методов отсечения

Запишем общую задачу целочисленного программирования: в области, определенной условиями

(11)

(12)

- целые, (13)

максимизировать функцию

(14)

Назовем для кратности задачу (11–14) (£^ц, C) – задачей. Соответствующую ей задачу без требования целочисленности переменных, т.е. задачу (11, 12, 14) назовем (£, C) – задачей. Поставим вопрос: нельзя ли решение (£^ц, C) – задачи получить путем решения некоторой специальным образом построенной задачи без требования целочисленности переменных и такой, что оптимальные решения исходной (£^ц, C) – задачи и задачи без требований целочисленности переменных будут совпадать. Другими словами: нельзя ли хорошо изученный аппарат решения задач линейного программирования приспособить к решению целочисленных задач. Принципиальный ответ на этот вопрос дает следующая теорема.

Теорема. Пусть £ – многогранник, £^ц – множество его целых точек, R – выпуклая, линейная оболочка множества £^ц, тогда:

1) R=R^ц – целочисленный многогранник;

2) R^ц = £^ц;

3) R* – множество опорных решений задачи (£^ц, C) содержится в многограннике R^ц.

Доказательство. Докажем, что R – целочисленный многогранник. По условию теоремы £ – многогранник, поэтому множество его целых точек (оно обозначено через £^ц) конечно. Поскольку R – выпуклая линейная оболочка этого конечного множества точек, R – тоже многогранник.

По самому определению выпуклой линейной оболочки, она содержит все опорные планы множества, на которое она натянута, т.е. многогранник R содержит все целочисленные точки £^ц. Поэтому R – целочисленный многогранник. Обозначим его через R^ц. Первая часть теоремы доказана.

Докажем, что R^ц совпадает с £^ц. Так как R – выпуклая оболочка точек множества £^ц, то £^ц ÍR^ц.

Покажем, что справедливо также и противоположное неравенство–включение, т.е. R^цÍ£^ц. Для этого выберем некоторый произвольный элемент х°ÎR^ц. Поскольку R^ц содержит все опорные решения задачи (£^ц, C), то х° удовлетворяет условиям задачи (£^ц, C), т.е. х°Î£^ц. Но поскольку произвольный элемент из R^цпринадлежит £^ц, то очевидно, что справедливоR^цÍ£^ц. Сопоставляя противоположные включения R^цÍ£^ц и £^цÍR^ц приходим к выводу: что £^ц=R^ц. Вторая часть теоремы также доказана.

Доказательство 3-го пункта теоремы является совершенно очевидным. Так как R^* – множество опорных решений задачи (£^ц, C), то R^*Í£^ц но £^ц=R^ц, поэтому R^*ÍR^ц

Теорема доказана.

Следствием из этой теоремы является тот вывод, что оптимальное решение задачи, областью определения которой является выпуклая оболочка, натянутая на область поиска целочисленного решения, совпадает с оптимальным решением исходной целочисленной задачи.

Доказанная теорема и следствие из нее показывают принципиальную возможность замены решения задачи типа (£^ц, C) некоторой процедурой построения и решения вспомогательной задачи типа (£, C), однако не дают алгоритма решений. К тому же построение выпуклой оболочки множества £^ц реальных задач – чрезвычайно сложная, а подчас практически неразрешимая задача,

В 1954 г. Дж. Данциг высказал идею о том, что построение выпуклой оболочки целочисленной области для задачи (£^ц, C) можно осуществлять поэтапно и решать получаемые при этом задачи. Однако при этом возникли вопросы как строить ограничения новой задачи и как обеспечить конечность процесса.

Ответ на эти вопросы был впервые получен Р. Гомори, который предложил алгоритмы решения целочисленных и. частично целочисленных задач.

Алгоритм Р. Гомори состоит из следующих процедур:

1. Решается (£, C) – задача, соответствующая исходной (£^ц, C) – задаче.

2. Полученное оптимальное решение (£, C) – задачи, если оно существует, проверяется на целочисленность. Если условие целочисленности выполняется по всем переменным, то оптимальное решение (£, C) – задачи есть оптимальное решение (£^ц, C) – задачи. Если условие целочисленности не выполняется хотя бы по одной координате, то переходят к третьему этапу. Если (£, C) – задача, оказывается неразрешимой, то (£^ц, C) – задача тоже решения не имеет.

3. Строится дополнительное ограничение, обладающее тем свойством, что с его помощью отсекается часть области, в которой содержится оптимальное решение (£, C) – задачи и не содержится ни одного допустимого решения (£^ц, C) – задачи. Процесс построения дополнительных ограничений и решения получаемых при этом (£, C) – задач продолжается до тех пор, пока не получим целочисленного решения или не убедимся в неразрешимости задачи.

При этом свойства, которыми должно обладать каждое из дополнительных ограничений при переходе от одной задачи к другой следующие:

1) дополнительное ограничение должно быть линейным, чтобы оставаться в области применимости аппарата линейного программирования;

2) дополнительное ограничение должно отсекать часть области, в которой не содержится допустимых решений целочисленной (£^ц, C) – задачи, но есть найденное оптимальное решение нецелочисленной (£, C) – задачи, т.е. ограничение должно обладать свойством правильности, которое не позволяет потерять оптимальное решение исходной (£^ц, C) – задачи.

Пусть х (£, C) – оптимальное решение (£, C) – задачи, которое является недопустимым решением для (£^ц, C) – задачи. Неравенство

(15)

определяет правильное отсечение, если удовлетворяет

а) условию отсечения: x(£, C) удовлетворяет неравенству (15)

б) условию правильности: любое допустимое решение задачи (£^ц, C), удовлетворяет неравенству (15).

Методы, основанные на использовании процедуры построения правильных отсечений, получили название методов отсечения.

3. Первый алгоритм Гомори

Следуя общей схеме методов отсечения, решим (£, C) – задачу (11, 12, 14), соответствующую (£^ц, C) – задаче (11–14). Пусть x(£, C) – ее оптимальное решение. Проанализируем координаты x(£, C) на целочисленность. Если все координаты вектора x(£, C) целые, то x(£, C) = x(£^ц, C). Если хотя бы одна координата, пусть x_i, будет нецелой, поступим следующим образом.

Обозначим через N совокупность небазисных переменных и на основании последней симплексной таблицы запишем разложение x_i по небазисным переменным x_i, jÎN

(16)

Так как x_i – нецелая величина, обозначим ближайшее целое число, не превосходящее x_i, через (x_i) и определим дробную часть: {x_i}= x_i- (x_i). Очевидно, (x_i)>0.

Покажем, что по i-и строке симплексной таблицы (£, C) – задачи (в которой стоит нецелая координата решения) можно определить дополнительное линейное ограничение, обладающее свойствами правильности.

Теорема. Пусть - допустимое решение (£^ц, C) – задачи, тогда соотношения

, (17)

, - целое,

определяют правильное отсечение.

Доказательство.

Запишем выражение (16) в виде:

Используя для этого выражения формулу (17), получим:

или

На основании предположений теоремы о допустимости решения

(£^ц, C) – задачи x_i – целое. Величины (x_io), - целые по определению, следовательно, z_i – тоже целое.

Итак, z_i определенное формулой (17), целое. Докажем что . Доказательство будем вести от противного. Пусть .-

Это значит, что . По определению дробной части . По условию теоремы x – допустимое решение (£^ц, C) – задачи, поэтому . Следовательно,

Тогда должно выполняться:

Итак, из предположения отрицательности z_i, сразу же получаем т.е. z_i – нецелое. Поскольку ранее было показано, что z_i, определенное формулой (17), является целым, то тем самым мы пришли к противоречию. Следовательно, предположение, что z_i < 0, неверное. Теорема доказана.

Следствие. Любое оптимальное решение x(£, C) (£, C) – задачи, не являющееся допустимым решением (£^ц, C) – задачи, неудовлетворяет условию правильного отсечения (17).

Доказательство. Пусть х (£, C) – оптимальное решение (£, C) – задачи, x_i₀ – дробное.

Покажем, что х (£, C) не удовлетворяет условию отсечения. Поскольку план оптимален, все небазисные переменные x_i, для jÎN равны нулю. Поэтому . Учитывая это, подставим x_io в формулу (17):

z_i(x (£, C))= – {x_i₀}+0<0,

что противоречит условию неотрицательности z_i. Следствие доказано.

Очевидно, что количество дополнительных ограничений будет нарастать по мере решения вспомогательных (£, C) – задач, оптимальные планы которых будут содержать нецелые координаты, т.е. возникает проблема размерности.

Р. Гомори предложил прием, позволяющий ограничить размеры рассматриваемых симплексных таблиц вспомогательных задач величиной (n+2) (k+1), где n – количество переменных (£, C) – задачи, k – число небазисных переменных ее. Этот прием основывается на том, что нас интересует дополнительное ограничение лишь как способ отсечения нецелочисленного оптимального решения вспомогательной задачи, полученной на данном шаге, и перехода к следующей задаче.

Последовательность (£, C) – задач пометим индексом k=0,1,…, соответствующим номеру итерации в последовательном приближении к решению исходной (£^ц, C) – задачи, и обозначим (£_k, C). При этом (£₀, C) – задача соответствует (£, C) – задаче (задаче без требования целочисленности).

Переменную z_i, которая определяется дополнительным линейным ограничением (7) и строится по некоторой нецелочисленной координате оптимального решения (£_k, C) – задачи (k =0, 1, 2,…) обозначим x_n₊_k₊_l.

Чтобы размерность последовательности (£_k, C) – задач не возрастала, вычеркнем из симплекс-таблицы переменную, по которой построено дополнительное линейное ограничение.

После сделанных замечаний перейдем непосредственно к изложению вычислительной схемы.

1. Решим (£_k, C) – задачу (вначале k = 0) методом последовательного улучшения плана.

Пусть в базис оптимального решения вошли векторы A_s₁,…, A_sm. Параметры последней симплексной таблицы обозначим через x_ij:

Если, все базисные составляющие оптимального решения x(£_k, C) (£_k, C) – задачи целые, то x(£_k, C) = x(£^ц, C). Если некоторая координата x_io оптимального решения x(£_k, C) нецелая, то перейдем к п. 2.

2. Если среди совокупности координат оптимального решения x(£_k, C) имеется единственная нецелая координата, то дополнительное линейное ограничение (17) строится по этой координате. Если нецелых координат в x(£_k, C) более одной, то выберем координату с наименьшим номером. Пусть ею оказалась x_i₀. Составим дополнительное линейное ограничение

(18)

(19)

3. Добавим условия (18, 19) к условиям (£_k, C) – задачи. Получим новую (£_k₊₁, C) – задачу. Так как оптимальное решение x(£_k, C) (£_k, C) – задачи определяло одну из вершин многогранника условий, то оно может быть выбрано в качестве первоначального опорного решения для вновь полученной задачи. А это означает, что последнюю симплексную таблицу (£_k, C) – задачи можно взять в качестве исходной для (£_k₊₁, C) – задачи, дополнив ее условием (18).

Итак, симплексная таблица для (£_k₊₁, C) – задачи получается из последней симплексной таблицы для (£_k, C) – задачи путем окаймления (i+1) – й строкой с элементами:

где – небазисные переменные (£_k, C) задачи.

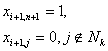
Получим новую задачу, переменными которой являются . Условия этой задачи разрешены относительно x_sl,…, x_sm переменных и новой переменной x_n₊_k₊₁, а линейная форма выражена через небазисные переменные (£_k, C) – задачи. Так как мы занимаемся максимизацией F(x) и решение х* для (£_k, C) – задачи оптимально, то все D_i > 0. Поэтому процесс перехода к новому решению (£_k₊₁, C) – задачи не может быть осуществлен по методу уточнения плана. В то же время и поэтому вектор А₀ симплексной таблицы не является опорным решением для (£_k₊₁, C) – задачи, так как решением называется вектор, все координаты которого неотрицательны и удовлетворяют условию принадлежности области £_k₊_l. Поэтому назовем полученный вектор псевдорешением задачи (£_k₊₁, C) и перейдем к дальнейшему преобразованию симплекс-таблицы.

Обозначим через k номер псевдорешения (£_k, C) – задачи; тогда направляющей строкой является i+k+1-я строка, k =0, 1, 2,…. Поэтому на каждом этапе преобразования таблицы вектор A_i₊_k₊_i будет выводиться из таблицы. Можно доказать, что через конечное число шагов либо будет найдено целочисленное решение, либо будет обнаружена ее неразрешимость, а тем самым неразрешимость (£^ц, C) – задачи.

Если решение (£_k, C) – задачи завершается построением оптимального целочисленного решения x*, то m, первых его компонент определяют решение целочисленной задачи; если среди координат х* есть дробные, то одна из дробных компонент (ранее определенным правилом) порождает дополнительное ограничение и процесс решения должен быть продолжен с новой окаймляющей строкой. Строка, используемая ранее для окаймления, вычеркивается и больше для построения расширенных задач не восстанавливается.

Процедуру решения (£_k, C) – задачи (k=0, 1,…) и анализа полученного решения назовем большой итерацией. Номер большой итерации совпадает с номером решаемой (£_k, C) – задачи.

Результатом большой итерации является переход к новой (£_k₊₁, C) – задаче либо окончание решения задачи.

Сделаем некоторые пояснения к блок-схеме алгоритма.

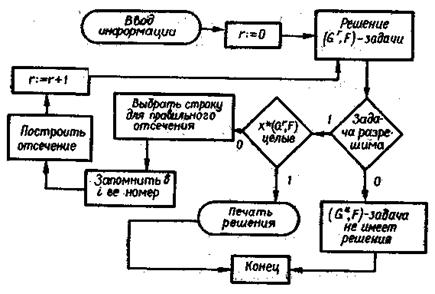
Введем: 1) ячейку i, в которой будем запоминать номер строки, на основании которой строится очередное дополнительное линейное ограничение, 2) счетчик r, соответствующий номеру проводимой большой итерации. Обозначим x*(£^r, C) оптимальное решение (£^r, C) – задачи. Заметим, что обозначение (£^r, C) – задача, эквивалентное (£_r, C), введено в блок-схеме для удобства записи.

При некоторых условиях удается доказать теорему о конечности первого алгоритма Гомори, которую мы приведем без доказательства.

Теорема. Пусть множество оптимальных планов задачи (£₀, C) ограничено и выполняются следующие условия:

1) с_i – целые коэффициенты целевой функции F(x) (i =1,2,…, n), строка целевой функции в симплексной таблице учитывается при выборе строки для построения правильного отсечения;

2) справедливо одно из двух утверждений: либо целевая функция ограничена снизу на С_o, либо задача (£^ц, C) имеет хотя бы один план х'.

Тогда первый алгоритм Гомори требует конечного числа больших итераций.

4. Второй алгоритм Гомори

Второй алгоритм Р. Гомори предназначается для решения задач, в которых требование целочисленности наложено на некоторые переменные (в частности и на все). Мы его рассмотрим применительно к задачам частично целочисленного типа, понимая, что вычислительная схема будет справедливой и для задач, полностью целочисленных.

Пусть в области, определенной условиями:

(20)

(21)

– целые, (22)

требуется максимизировать функцию

(23)

Метод решения задачи (20–23) основывается на той же идее, что и метод решения полностью целочисленных задач. А именно: строится область £_k, которая при k = 0 определяется условиями (20–21); решается полученная при этом задача линейного программирования (20–21, 23). Если задача (20–21, 23) оказывается разрешимой, то полученное оптимальное решение ее анализируется на допустимость для исходной задачи целочисленного программирования (20–23). Если найденное решение оказывается целочисленным, то одновременно оно будет оптимальным для (20–23). Если оптимальное решение (£_k, C) – задачи оказывается недопустимым для исходной задачи (20–23), то осуществляется построение правильного отсечения и переход к решению новой задачи,

Второй алгоритм Р. Гомори формулируется в виде следующей теоремы:

Теорема. Пусть х(£_k, C) – оптимальное решение (£_k, C) – задачи, – элементы соответствующей ему симплексной таблицы. Если – нецелое , то

(24)

– целое, (25)

где

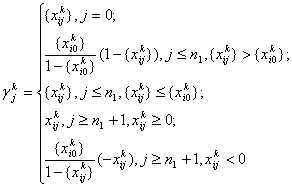(26)

определяет правильное отсечение. Блок-схема второго алгоритма Р. Гомори аналогична блок-схеме первого алгоритма Р. Гомори и отличается лишь правилом построения коэффициентов правильного отсечения.

Правило построения правильного отсечения

Пусть x(£_k, C) не удовлетворяет условию целочисленности, – элементы симплексной таблицы, соответствующей полученному оптимальному решению (£_k, C) – задачи. Выберем i₀=min {iiÎ(1, 2,…, ), x_i₀^k– нецелое} и строим правильное отсечение по формулам (24 – 26).

Условия конечности второго алгоритма Гомори:

1) Целевая функция F(x) удовлетворяет условию целочисленности. Это учитывается при выборе строки kдля построения правильного отсечения.

2) Выполнено по крайней мере одно из двух условий:

2') целевая функция ограничена снизу на многогранном множестве £= £₀;

2») задача (£₀^ц, C)имеет по крайней мере один план.

С помощью второго алгоритма Гомори можно (в случае n₁=n) решать и полностью целочисленную задачу линейного программирования. Однако в этом случае нет оснований для сравнения эффективности второго и первого алгоритмов Гомори.

5. Алгоритм Дальтона и Ллевелина

Второй алгоритм Гомори имеет дело с частично целочисленными задачами линейного программирования. Дальтон и Ллевелин рассматривают 0 олее широкий класс задач – частично дискретные задачи линейного программирования и применительно к ним модифицируют второй алгоритм Гомори.

Напомним, что решением задачи дискретного программирования будем называть вектор, координаты которого принадлежат £^ц области вида:

(27)

(28)

(29)

и максимизирует значение функции

(30)

Будем предполагать, что проранжированы, т.е. и являются наперед заданными числами.

Теорема. Пусть x(£_k, C) – оптимальное решение задачи (27–28, 30), – элементы симплексной таблицы, соответствующей ему.

Если x(£_k, C) является недопустимым решением задачи (27–30) и , тогда, используя i-ю строку симплексной таблицы, можно построить отсечение, обладающее свойством правильности по формулам:

(31)

(32)

где

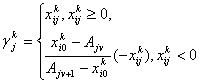(33)

Доказательство. Проверим вначале условие отсечения. Пусть в оптимальном решении x(£_k, C) координата не удовлетворяет условию (29). Покажем, что в этом случае вектор х(£_k, C) не удовлетворяет условиям (31, 32). Поскольку N_k – множество индексов небазисных переменных x_i_, которые в оптимальном решении равны нулю, то равенство (31) принимает вид и будет отрицательным согласно условию теоремы. Следовательно, , т.е. условие отсечения не выполняется.

Проверим условие правильности. Для этого покажем, что любое допустимое решение задачи (27–30) удовлетворяет условиям (31, 32).

Запишем разложение для координаты допустимого решения задачи (27–30) по небазисным переменным

(34)

и рассмотрим два случая: a) ; б) . Введем обозначения:

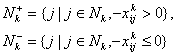
и представим (34) в виде

где

Очевидно, так как .

Рассмотрим случай а): , или что все равно, .

Отсюда Но поэтому

(35)

Домножим обе части (35) на неотрицательную величину и сложим с неотрицательной величиной :

(36)

Рассмотрим случай б): или, что все равно, Так как по определению , то Умножим обе части неравенства на неотрицательную величину и на -1, получим . Прибавляя к полученному выражению неравенство , получим

(37)

Таким образом, в а) и в б) случаях пришли к одному и тому же неравенству (36) и (37). Пользуясь ранее введенными обозначениями, их можно записать

(38)

Формула (38) определяет правильные отсечения. Сравнивая ее с выражением (31–32), приходим к выводу, что коэффициенты определяются следующим образом:

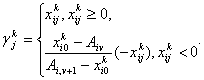
Теорема доказана.

Алгоритм Дальтона – Ллевелина может быть описан следующим образом.

1. Решается (£_k, C) – задача (27–30) (вначале k = 0). Пусть x(£_k, C), k = 0, 1, 2,… оптимальное решение (£_k, C) – задачи, – симплексная таблица.

2. Проверяется условие допустимости по всем координатам оптимального вектора решения х(£_k, C) (£_k, C) – задачи. Если условие допустимости выполняется, то полученное решение является оптимальным решением исходной задачи (27–30). Если условие допустимости не выполняется хотя бы по одной координате, осуществляется переход к 3.

3. Пусть не удовлетворяет условию допустимости. Тогда выбирается

i₀= min {i| 1<i<₁, х_j₀^k – не удовлетворяет (29)}.

4. Для выбранного номера i=i₀ строится правильное отсечение, т.е. вводится дополнительная переменная

где определяется формулой (33),

5. Добавляем линейное ограничение, определяющее правильное отсечение, к условиям (£_k, C) – задачи и получаем новую (£_k₊₁, C) – задачу. Полагая k = k + 1, переходим к п. 1.

Приведем без доказательства теорему о конечности алгоритма.

Теорема. Если: коэффициенты целевой функции дискретны; F(x) ограничена снизу на многогранном множестве £; задача (£, C) имеет по крайней мере одно решение; выбор строки для построения правильного отсечения производится по правилу минимального номера и (£_k, C) – задачи решаются методом последовательного уточнения оценок, то алгоритм Дальтона и Ллевелина сходится.

6. Алгоритм Данцига

Способ построения правильных отсекающих плоскостей, предложенный Данцигом значительно проще, чем все изложенные выше способы. Но, как показали Гомори и Гофман, конечность алгоритма Данцига гарантируется лишь для очень узкого класса задач. На примере алгоритма Данцига видно, насколько тонким является вопрос о построении правильных отсечений и сколь осторожно следует подходить к различным упрощенным алгоритмам.

Рассматривается полностью целочисленная задача линейного программирования:

Максимизировать

(39)

при условиях

(40)

(41)

– целые, (42)

Ранг матрицы считаем равным m.

Теорема. Пусть x(£_r, C)=x^r является оптимальным опорным планом задачи (£_r, C) и x^r не удовлетворяет условию целочисленности, N_r – множество индексов, нумерующих небазисные переменные, соответствующие x^r.

Тогда неравенство

(43)

является правильным отсечением.

Правильное отсечение, отсекающее нецелочисленный оптимум x(£_r, C) задачи (£_r, C), можно записать следующим образом:

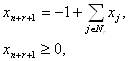
– целое.

Заметим, что каждая из вновь вводимых переменных однозначно определяется заданием переменных, так что .

Обозначим через упорядоченные в порядке возрастания компоненты плана x задачи (39) – (41), так что

(44)

Положим

(45)

Лемма. Если для некоторого плана x задачи (39) – (41)

, (46)

то

(47)

Доказательство проведем по индукции. Сначала докажем, что

(47¢)

По определению

(48)

Так как ранг матрицы равен m, то

где – число элементов множества . Из определения чисел получаем

(49)

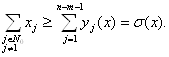(50)

Из (48), (49), (50) и (46) имеем

Лемма доказана при р=1.

Теперь допустим, что лемма верна при , и докажем ее при :

Лемма доказана.

Пользуясь леммой, докажем две теоремы.

Теорема 1. Если каждый оптимальный план задачи (39) – (42) содержит не менее (m+2) положительных компонент, то алгоритм Данцига не будет конечным.

Доказательство. Допустим, что на s-й итерации ал