Математические методы экономики
Математические методы экономики.
Моделирование сферы потребления. Потребительские предпочтения. Кривые безразличия. Предельная норма замещения благ. Функция полезности и её свойства. Бюджетное ограничение. Равновесие потребителя. Реакция потребителя на изменение цен и дохода. Уравнение Слуцкого. Эффекты дохода и замены. Классификация благ. Индивидуальный и рыночный спрос. Эластичность спроса по ценам и доходу потребителя. Построение функции спроса по опытным данным.
В условиях рыночной системы управления производственной и сбытовой деятельностью предприятий и фирм в основе принятия хозяйственных решений лежит рыночная информация, а обоснованность решений проверяется рынком в ходе реализации товаров и услуг. При таком подходе основой предпринимательской деятельности становится изучение потребительского спроса.
Рассмотрим некоторые вопросы моделирования спроса и потребления.
Уровень потребления общества можно выразить целевой функцией потребления U = U(Y), где Y ![]() О - вектор переменных разнообразных товаров и услуг. Ряд свойств этой функции удобно изучать, используя геометрическую интерпретацию уравнений U(Y) = С, где С - меняющийся параметр, характеризующий значение (уровень) целевой функции потребления (например, доход или уровень материального благосостояния).
О - вектор переменных разнообразных товаров и услуг. Ряд свойств этой функции удобно изучать, используя геометрическую интерпретацию уравнений U(Y) = С, где С - меняющийся параметр, характеризующий значение (уровень) целевой функции потребления (например, доход или уровень материального благосостояния).
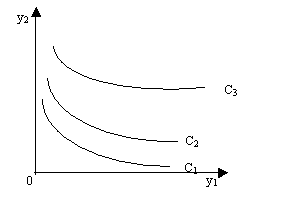
В совокупности потребительских благ каждому уравнению U(Y) = С соответствует определенная поверхность равноценных, или безразличных, наборов благ, которая называется поверхностью безразличия. Для наглядности рассмотрим пространство двух благ, например, в виде двух агрегированных групп товаров: продукты питания (y1) и непродовольственные товары, включая услуги (у2 ). Тогда уровни целевой функции потребления можно изобразить на плоскости в виде кривых безразличия, соответствующих различным значениям С (рис. 8.1, где С1 < С2 < Сз).
|
Рис. 8.1. График кривых безразличия
Из основных свойств целевой функции потребления можно отметит следующие:
1. функция U(Y) является возрастающей функцией всех своих аргументов, т.е. увеличение потребления любого блага при неизменном уровне потребления всех других благ увеличивает значение данной функции;
2. кривые безразличия не могут пересекаться, т.е. через одну точку совокупности благ (товаров, услуг) можно провести только одну поверхность безразличия;
3. кривые безразличия имеют отрицательный наклон к каждой оси координат, при этом абсолютный наклон кривых уменьшается при движении в положительном направлении по каждой оси, т.е. кривые безразличия являются выпуклыми кривыми.
Методы построения целевой функции потребления основаны на обобщении опыта поведения потребителей и тенденций покупательского спроса в зависимости от уровня благосостояния.
Рассмотрим моделирование поведения потребителей в условиях товарно-денежных отношений на базе целевой функции потребления. В основе модели поведения потребителей лежит гипотеза, что потребители, осуществляя выбор товаров при установленных ценах и имеющемся доходе, стремятся максимизировать уровень удовлетворения своих потребностей.
Пусть в совокупности п видов товаров исследуется поведение потребителей. Обозначим спрос потребителей через вектор Y = (y1, у2,...,yn), а цены на различные товары - через вектор Р = (р1, р2,…,pп). Пусть D - величина дохода. Тогда потребители могут выбирать только такие комбинации товаров, которые удовлетворяют ограничению 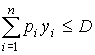 , называемому бюджетным ограничением.
, называемому бюджетным ограничением.
Пусть U(Y) целевая функция потребления. Тогда простейшая модель поведения потребителей в векторной форме можно записать в виде:
![]() (8.1)
(8.1)
Геометрическая интерпретация модели (8.1) для двух агрегированных групп товаров представлена на рис. 8.2.
Линия АВ (в других вариантах А1В1, А2В2) соответствует бюджетному ограничению и называется бюджетной линией. Выбор потребителей ограничен треугольником АОВ (A1OB1, A2OB2).
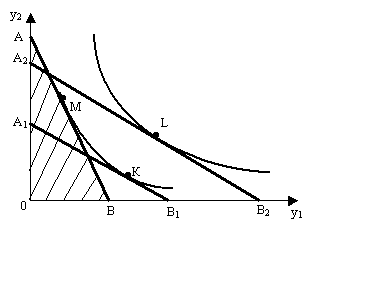
Рис. 8.2. График простейшей модели поведения потребителя
Набор товаров М, соответствующий точке касания прямой АВ с наиболее отдаленной кривой безразличия, является оптимальным решением (в других вариантах это точки К и L). Легко заметить, что линии АВ и A1B1 соответствуют одному и тому же размеру дохода и разным ценам на товары y1 и у2; линия A2B2 соответствует большему размеру дохода.
На основе теории нелинейного программирования, можно определить математические условия оптимальности решений для модели (8.1). С задачей нелинейного программирования связывается так называемая функция Лагранжа, которая для задачи (8.1) имеет вид
L(Y, l,) = U(Y) + l(D - PY),
где множитель Лагранжа l является оптимальной оценкой дохода.
Обозначим частные производные функции U(Y) через Ui: ![]()
Они представляют собой предельные полезные эффекты (предельные полезности) соответствующих потребительских благ и показывает на сколько единиц увеличивается целевая функция потребления при увеличении использования i-гоблага (товара) на некоторую условную «малую единицу».
Необходимыми условиями того что вектор Y0 будет оптимальным решением, является условия Куна-Таккера:
![]()
при этом![]()
![]() (товар приобретается)
(товар приобретается)
![]() (товар не приобретается) (8.2)
(товар не приобретается) (8.2)
![]()
Последнее из соотношений (8.2) соответствует полному использованию дохода, и для этого случая очевидно неравенство ![]() .
.
Из условий оптимальности (8.2) следует, что
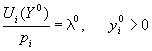
Это означает, что потребители должны выбрать товары таким образом, чтобы отношение предельной полезности к цене товара было одинаковым для всех приобретаемых товаров, т.е. в оптимальном наборе предельные полезности выбираемых товаров должны быть пропорциональны ценам.
Функциями спроса называются функции, отражающие зависимость объема спроса на отдельные товары и услуг от совокупности факторов, влияющих на него. Рассмотрим построение функций спроса в зависимости от двух факторов – дохода и цен.
Пусть в модели (8.1) цены и доход рассматриваются как меняющиеся параметры. Переменную дохода будем обозначать Z. Тогда решением оптимизационной задачи (8.1) будет векторная функция ![]() компонентами которой являются функции спроса на определенный товар от цен и дохода:
компонентами которой являются функции спроса на определенный товар от цен и дохода:
![]()
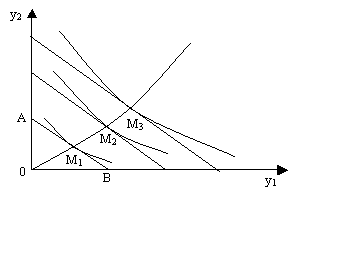
Рассмотрим частный случай, когда вектор цен является неизменным, а доход изменяется. Для двух товаров этот случай представлен на рис. 8.3. Если по оси абсцисс отложить количество единиц товара y1, которое можно приобрести на имеющий доход Z (точка В), а по оси ординат – то же самое для товара y2 (точка А), то прямая линия АВ, называемой бюджетной линией, показывает любую комбинацию количеств этих двух товаров, которую можно купить за сумму денег Z. При увеличении дохода бюджетные линии перемещаются параллельно самим себе, удаляясь от начала координат. Вместе с ними перемещаются соответствующие кривые безразличия. Точками оптимума спроса потребителей для соответствующих размеров дохода будут в данном случае точки M1, M2, M3. При нулевом доходе спрос на оба товара нулевой. Кривая, соединяющая точки 0, M1, M2, M3, является графическим отображением векторной функции спроса и дохода при заданном векторе цен.
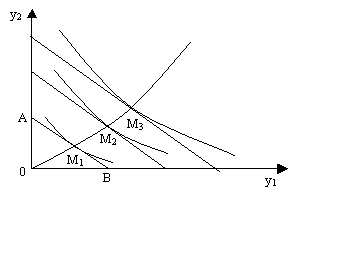
Рис. 8.3. График функции спроса и дохода (для двух товаров у1 и у2)
Однофакторные функции спроса от дохода широко применяются при анализе покупательского спроса. Соответствующие этим функциям кривые ![]() называются кривыми Энгеля (по имени немецкого экономиста). Формы этих кривых для различных товаров могут быть различны. Если спрос на данный товар возрастает примерно пропорционально доходу, то функция будет линейной (рис. 8.4а). Если по мере роста дохода спрос на данную группу товаров возрастает все более высокими темпами, то кривая Энгеля будет выпуклой (рис. 8.4б). Если рост значений спроса, начиная с определенного момента, по мере насыщения спроса отстает от роста дохода, то кривая Энгеля имеет вид вогнутой кривой (рис. 8.4в).
называются кривыми Энгеля (по имени немецкого экономиста). Формы этих кривых для различных товаров могут быть различны. Если спрос на данный товар возрастает примерно пропорционально доходу, то функция будет линейной (рис. 8.4а). Если по мере роста дохода спрос на данную группу товаров возрастает все более высокими темпами, то кривая Энгеля будет выпуклой (рис. 8.4б). Если рост значений спроса, начиная с определенного момента, по мере насыщения спроса отстает от роста дохода, то кривая Энгеля имеет вид вогнутой кривой (рис. 8.4в).
предложил специальные виды функции спроса (функции Торнквиста) для трех групп товаров: первой необходимости, второй необходимости, предметов роскоши.
Важным показателем функции спроса является коэффициент эластичности. Коэффициент эластичности спроса от дохода показывает на сколько процентов, изменится спрос, если доход увеличится на 1% (при прочих не изменяющихся факторах), и вычисляется по формуле:
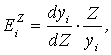
где ![]() - коэффициент эластичности для i-го товара (группы товаров) по доходу Z;yi - спрос на i-й товар, являющийся функцией дохода:
- коэффициент эластичности для i-го товара (группы товаров) по доходу Z;yi - спрос на i-й товар, являющийся функцией дохода: ![]() .
.
|
Аналогичный принцип разграничения групп товаров по типам функций спроса от дохода использовал шведский экономист Л. Торнквист, который
Коэффициенты эластичности спроса от дохода различны по величине для разных товаров, вплоть до отрицательных значений, когда с ростом доходов потребление уменьшается. Принято выделять четыре группы товаров в зависимости от коэффициента эластичности спроса на них от дохода:
· малоценные товары (![]() );
);
· товары с малой эластичностью (![]() );
);
· товары со средней эластичностью (![]() близки к единице);
близки к единице);
· товары с высокой эластичностью (![]() ).
).
К малоценным товарам (с отрицательной эластичностью спроса от дохода) относятся хлеб, а также низкосортные товары. По результатам обследований, коэффициенты эластичности для основных продуктов питания находятся в интервале от 0,4 до 0,8, по одежде, тканям, обуви - в интервале от 1,1 до 1,3 и т.д. По мере увеличения дохода спрос перемещается с товаров первой и второй групп на товары третьей и четвертой групп, при этом потребление товаров первой группы по абсолютным размерам сокращается.
Перейдем к рассмотрению и анализу функций покупательского спроса от цен на товары. Из модели поведения потребителей (8.1) следует, что спрос на каждый товар в общем случае зависит от цен на все товары (вектора Р), однако построить функции общего вида ![]() очень сложно. Поэтому в практических исследованиях ограничиваются построением и анализом функций спроса для отдельных товаров в зависимости от изменения цен на этот же товар или группу взаимозаменяемых товаров:
очень сложно. Поэтому в практических исследованиях ограничиваются построением и анализом функций спроса для отдельных товаров в зависимости от изменения цен на этот же товар или группу взаимозаменяемых товаров: ![]() .
.
Для большинства товаров действует зависимость: чем выше цена, тем ниже спрос, и наоборот. Относительное изменение объема спроса при изменении цены данного товара или цен других связанных с ним товаров характеризует коэффициент эластичности спроса от цен.Этот коэффициент эластичности удобно трактовать как величину изменения спроса в процентах при изменении цены на 1%.
Для спроса yi на i-й товар относительно его собственной цены pi коэффициент эластичности исчисляется по формуле:
 (8.4)
(8.4)
Значения коэффициентов эластичности спроса от цен практически всегда отрицательны. Однако по абсолютным значениям этих коэффициентов товары могут существенно различаться друг от друга. Их можно разделить на три группы:
- товары с неэластичным спросом в отношении цены ![]() ;
;
- товары со средней эластичностью спроса от цены (![]() близки к -1);
близки к -1);
- товар с высокой эластичностью спроса ![]() .
.
В товарах эластичного спроса повышение цены на 1% приводит к снижению спроса более чем на 1% и, наоборот, понижение цены на 1% приводит к росту покупок больше чем на 1%. Если повышение цены на 1% влечет за собой понижение спроса менее чем на 1%, то говорят, что этот товар неэластичного спроса.
Рассмотрим влияние на спрос на какой-либо товар изменения цен на другие товары. Коэффициент, показывающий, на сколько процентов изменится спрос на данный товар при изменении на 1% цены на другой товар при условии, что другие цены и доходы покупателей остаются прежними, называется перекрестным коэффициентом эластичности. Для спроса уi на i-й товар относительно цены pj на j-й товар (![]() ) перекрестный коэффициент эластичности рассчитывается по формуле:
) перекрестный коэффициент эластичности рассчитывается по формуле:
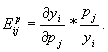 (8.5)
(8.5)
По знаку перекрестных коэффициентов эластичности товары можно разделить на взаимозаменяемые и взаимодополняемые. Если ![]() , это означает, что i-й товар заменяет в потреблении товар j, т.е. на товар i переключается спрос при увеличении цены на товар j. Примером взаимозаменяемых товаров могут служить многие продукты питания.
, это означает, что i-й товар заменяет в потреблении товар j, т.е. на товар i переключается спрос при увеличении цены на товар j. Примером взаимозаменяемых товаров могут служить многие продукты питания.
Если ![]() , это служит признаком того, что i-й товар в процессе потребления дополняет товар j, т.е. увеличение цены на товар j приводит к уменьшению спроса на товар i. В качестве примера можно привести такие взаимодополняемые товары, как автомобили и бензин, чай и сахар.
, это служит признаком того, что i-й товар в процессе потребления дополняет товар j, т.е. увеличение цены на товар j приводит к уменьшению спроса на товар i. В качестве примера можно привести такие взаимодополняемые товары, как автомобили и бензин, чай и сахар.
Спрос во многом определяет стратегию и тактику организации производства и сбыта товаров и услуг. Учет спроса, обоснованное прогнозирование его на краткосрочную и долгосрочную перспективу - одна из важнейших задач различных организаций и фирм.
Состав и уровень спроса на тот или иной товар зависят от многих факторов, как экономических, так и естественных. К экономическим факторам относятся уровень производства (предложения) товаров и услуг (обозначим этот фактор в общем виде П), уровень денежных доходов отдельных групп населения (D), уровень и соотношение цен (Р). К естественным факторам относятся демографический состав населения, в первую очередь размер и состав семьи (S), а также привычки и традиции, уровень культуры, природно-климатические условия и т.д.
Экономические факторы очень мобильны, особенно распределение населения по уровню денежных доходов. Естественные же факторы меняются сравнительно медленно и в течение небольшого периода (до 3-5 лет) не оказывают заметного влияния на спрос. Исключение составляет демографический состав населения. Поэтому в текущих и перспективных прогнозах спроса все естественные факторы, кроме демографических, целесообразно учитывать сообща, введя фактор времени (t).
Общем виде спрос определяется в виде функции перечисленных выше факторов:
у = f(П,D,P, S,t). (8.6)
Поскольку наибольшее влияние на спрос оказывает фактор дохода, многие расчеты спроса и потребления осуществляются в виде функции от душевого денежного дохода: у = f(D).
Наиболее простой подход к прогнозированию спроса на небольшой период времени связан с использованием так называемых структурных моделей спроса. При построении модели исходят из того, что для каждой экономической группы населения по статистическим бюджетным данным может быть рассчитана присущая ей структура потребления. При этом предполагается, что на изучаемом отрезке времени заметные изменения претерпевает лишь доход, а цены, размер семьи и прочие факторы принимаются неизменными. Изменение дохода, например его рост, можно рассматривать как перемещение определенного количества семей из низших доходных групп в высшие. Другими словами, изменяются частоты в различных интервалах дохода: они уменьшаются в нижних и увеличиваются в верхних интервалах. Семьи, которые попадают в новый интервал, будут иметь ту же структуру потребления и спроса, какая сложилась у семей с таким же доходом к настоящему времени.
Таким образом, структурные модели рассматривают спрос как функцию только распределения потребителей по уровню дохода. Имея соответствующие структуры спроса, рассчитанные по данным статистики бюджетов, и частоты распределения потребителей по уровню дохода, можно рассчитать общую структуру спроса. Если обозначить структуру спроса в группе семей со средним доходом Di через r(Di), а частоты семей с доходом Di через ![]() , то общая структура спроса R может быть рассчитана по формуле:
, то общая структура спроса R может быть рассчитана по формуле:
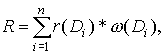 (8.7)
(8.7)
где п - количество интервалов дохода семей.
Структурные модели спроса - один из основных видов экономико-математических моделей планирования и прогнозирования спроса и потребления. В частности, широко распространены так называемые компаративные (сравнительные) структурные модели, в которых сопоставляются структуры спроса данного исследуемого объекта и некоторого аналогового объекта. Аналогом обычно считаются регион или группа населения с оптимальными потребительскими характеристиками.
Наряду со структурными моделями в планировании и прогнозировании спроса используются конструктивные модели спроса. В основе их лежат уравнения бюджета населения, т.е. такие уравнения, которые выражают очевидное равенство общего денежного расхода (другими словами, объема потребления) и суммы произведений количества каждого потребленного товара на его цену. Если Z - объем потребления, т - количество разных видов благ, qi - размер потребления i-го блага, pi - цена i-го блага, то конструктивная модель спроса может быть записана следующим образом:
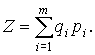
Эти модели, называемые также моделями бюджетов потребителей, играют важную роль в планировании потребления. Одной из таких моделей является, например, всем известный прожиточный минимум. К таким моделям относятся также рациональные бюджеты, основанные на научных нормах потребления, прежде всего продуктов питания, перспективные бюджеты (например, так называемый бюджет достатка) и др.
В практике планирования и прогнозирования спроса кроме структурных и конструктивных моделей применяются также аналитические модели спроса и потребления, которые строятся в виде однофакторных и многофакторных уравнений, характеризующих зависимость потребления товаров и услуг от тех или иных факторов
Моделирование конфликтов в финансово-экономической сфере. Основные понятия и определения теории игр. Классификация игр. Решение матричных игр с седловой точкой. Решение матричных игр без седловой точки. Смешанные стратегии. Теорема Дж. фон Неймана о существовании решения в смешанных стратегиях.
При управлении производством принимать решения очень часто приходится не имея достаточной информации, то есть в условиях неопределенности и риска.
Методами обоснования решений в условиях неопределенности и риска занимается математическая теория игр.
В теории игр рассматриваются такие ситуации, когда имеются два участника выполнения операции, каждый из которых преследует противоположные цели. В качестве участников могут выступать коллективы, конкурирующие предприятия и т. д. Во всех случаях предполагается, что операция проводится против разумного противника (конкурента), преследующего свои собственные цели и сознательно противодействующего достижению цели другим участником.
Так как цели противоположны, а результат мероприятия каждой из сторон зависит от действий конкурента, то эти действия называют конфликтными ситуациями. В конфликтной ситуации сталкиваются противоположные интересы двух участников. Формализованная (схематизированная) модель конфликтной ситуации называется игрой. Результат игры - победа или поражение, которые не всегда имеют количественное выражение, можно выразить (условно) числами (например, в шахматах: 1, 0, 1/2).
Игра называется игрой с нулевой суммой, если один из игроков выигрывает ровно столько, сколько проигрывает другой.
Развитие игры во времени представляется как ряд последовательных «ходов». Ходы могут быть сознательные и случайные. Случайный ход - результат, получаемый не решением игрока, а каким-либо механизмом случайного выбора (покупательский спрос, задержка с поставкой материалов и т.п.). Сознательный ход - выбор игроком одного из возможных вариантов действия (стратегии) и принятие решения об его осуществлении.
Возможные варианты (исходы) игры сводятся в прямоугольную таблицу (табл. 5.1.1) - платежную матрицу, в которой строки соответствуют различным стратегиям игрока А, столбцы - стратегиям игрока ![]() . Для условности предположим, что игрок А – выигрывает, а игрок В – проигрывает.
. Для условности предположим, что игрок А – выигрывает, а игрок В – проигрывает.
В результате выбора игроками любой пары стратегий Ai и Bj (i =1,…, m j = 1,…,n) однозначно определяется исход игры qij.
Цель теории игр - выработка рекомендаций для различного поведения игроков в конфликтной ситуации, то есть выбор оптимальной стратегии для каждого из них.
Для нахождения оптимальной стратегии необходимо проанализировать все возможные стратегии и рассчитывать на то, что разумный противник на каждую из них будет отвечать такой, при которой выигрыш игрока А минимален. Обычно минимальные числа в каждой строке обозначаются ![]() и выписываются в виде добавочного столбца матрицы (табл. 5.1.2).
и выписываются в виде добавочного столбца матрицы (табл. 5.1.2).
Они обозначают минимально-возможный выигрыш игрока А при соответствующей стратегии Аi. В каждой строке будет свое![]() . Так как игрок А выигрывает, то предпочтительной для игрока А является стратегия, при которой
. Так как игрок А выигрывает, то предпочтительной для игрока А является стратегия, при которой ![]() обращается в максимум, то есть
обращается в максимум, то есть ![]() или
или ![]() ,
,
где ![]() - максиминный выигрыш (максимин), а соответствующая ей стратегия - максиминная.
- максиминный выигрыш (максимин), а соответствующая ей стратегия - максиминная.
|
|
| … |
|
|
|
| … |
|
|
|
| … |
|
| … | … | … | … | … |
|
|
| … |
|
Таблица 5.2.2
|
| … |
|
| |
|
|
| … |
|
|
|
|
| … |
|
|
| … | … | … | … | … |
|
|
| … |
|
|
|
|
| … |
|
Если придерживаться максиминной стратегии, то при любом поведении стороны В (конкурента) гарантирован выигрыш, во всяком случае не меньше ![]() . Поэтому
. Поэтому ![]() называют также ценой игры - тот гарантированный минимум, который можно обеспечить при наиболее осторожной (перестраховочной) стратегии.
называют также ценой игры - тот гарантированный минимум, который можно обеспечить при наиболее осторожной (перестраховочной) стратегии.
Очевидно, что аналогичные распределения можно провести и для конкурента В, который должен рассмотреть все свои стратегии, выделяя для каждой из них максимальные значения проигрыша: ![]() (последняя строка матрицы).
(последняя строка матрицы).
Из всех значений ![]() находят минимальное:
находят минимальное:
![]() ,
,
которое дает минимаксный выигрыш или минимакс.
Такая ![]() -стратегия - минимаксная, придерживаясь которой сторона В гарантировано, что в любом случае проиграет не больше
-стратегия - минимаксная, придерживаясь которой сторона В гарантировано, что в любом случае проиграет не больше ![]() . Поэтому
. Поэтому ![]() называют верхней ценой игры.
называют верхней ценой игры.
Если ![]() , то число С называют чистой ценой игры или седловой точкой.
, то число С называют чистой ценой игры или седловой точкой.
Для игры с седловой точкой нахождение решения состоит в выборе пары максиминной и минимаксной стратегий, которые являются оптимальными, так как любое отклонение от этих стратегий приводит к уменьшению выигрыша первого игрока и увеличению проигрыша второго игрока по сравнению с ценой игры С.
Однако не все матрицы имеют седловую точку. Тогда решение находят, применяя смешанные стратегии, то есть чередуя случайным образом несколько чистых стратегий (гибкая тактика).
Вектор, каждая из компонент которого показывает относительную частоту использования игроком соответствующей чистой стратегии, называют смешанной стратегией данного игрока.
Из этого определения следует, что сумма компонент этого вектора равна единице, а сами компоненты не отрицательны.
Обычно смешанную стратегию первого игрока обозначают как вектор
![]() , а второго игрока - как вектор
, а второго игрока - как вектор ![]() , где
, где 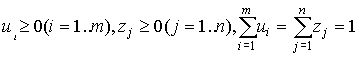 . (5.1.1).
. (5.1.1).
Если u° - оптимальная стратегия первого игрока, z° - оптимальная стратегия второго игрока, то число 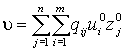 - называют ценой игры.
- называют ценой игры.
Для того чтобы число ![]() - было ценой игры, а u° и z° — оптимальными стратегиями, необходимо и достаточно выполнение неравенств:
- было ценой игры, а u° и z° — оптимальными стратегиями, необходимо и достаточно выполнение неравенств:
![]() , (5.1.2)
, (5.1.2)
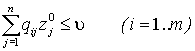 . (5.1.3)
. (5.1.3)
Если один из игроков применяет оптимальную смешанную стратегию, то его выигрыш равен цене игры и вне зависимости от того, с какими частотами будет применять второй игрок стратегии, вошедшие в оптимальную, в том числе и чистые стратегии
Внимание к седловым точкам в теории игр традиционно. Объясняется это недоверием к максимину, как к принципу оптимального выбора в том случае, когда нет седловой точки. Поэтому естественно стремление заполнить промежуток между максимином и минимаксом путем применения смешанных стратегий.
Однако, не следует забывать, что:
1) применение смешанных стратегий рисковано, когда игра не повторяется;
2) если игра повторяется, надо иметь уверенность, что у противника нет информации о конкретных решениях другого игрока;
3) противник не обязан применять смешанные стратегии, равно как и стремиться к цели, противоположной цели другого игрока.
Обозначим смешанную стратегию первого игрока = {i}, ![]() где i - вероятность применения i-й стратегии,
где i - вероятность применения i-й стратегии, 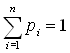 ,
, ![]() . Пусть смешанная стратегия второго игрока
. Пусть смешанная стратегия второго игрока ![]() ,
, ![]() , qj - вероятность применения j-й стратегии,
, qj - вероятность применения j-й стратегии, 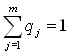 ,
, ![]() . Р и Q определяют математическое ожидание платежа:
. Р и Q определяют математическое ожидание платежа:
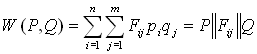 .
.
Теорема фон Неймана. Любая матричная игра имеет седловую точку в смешанных стратегиях.
Доказательство. Множества M и N ограничены и замкнуты, так как ![]() ,
, ![]() , а функция W непрерывна по P и Q . W линейна по P при фиксированных Q, следовательно, вогнута по P при фиксированных Q. Аналогично W выпукла по Q при фиксированных P. M и N выпуклы.
, а функция W непрерывна по P и Q . W линейна по P при фиксированных Q, следовательно, вогнута по P при фиксированных Q. Аналогично W выпукла по Q при фиксированных P. M и N выпуклы.
Действительно, рассмотрим такие ![]() и
и ![]() , что
, что 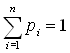 ,
, 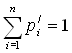 , тогда
, тогда ![]() ,
, ![]() .
.
Складывая, получим ![]() .
.
Кроме того, ![]() .
.
Следовательно, при![]() и
и ![]()
![]()
тоже смешанная стратегия.
Применяя фундаментальную теорему, получим то, что требуется доказать:
![]() .
.
Опираясь на доказанную теорему, можно быть уверенным, что решение игры в смешанных страте