Розвиток умінь розв’язувати задач на пропорційне ділення у початковій школі

ЗМІСТ

ВСТУП

РОЗДІЛ 1. ЗАГАЛЬНІ ПИТАННЯ НАВЧАННЯ РОЗВ’ЯЗУВАННЯ ЗАДАЧ

1.1 Система арифметичних задач у програмі з математики в початковій школі

1.2 Ступені роботи над текстовими задачами

РОЗДІЛ 2. МЕТОДИЧНА РОБОТА НАД ЗАДАЧАМИ НА ПРОПОРЦІЙНЕ ДІЛЕННЯ

2.1 Види задач на пропорційне ділення та способи їх опрацювання

2.2 Формування умінь розв’язувати задачі на пропорційне ділення

2.3 Результати експериментального дослідження

ВИСНОВКИ

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ

ВСТУП

Актуальність теми. Демократизація освіти вимагає від педагогічної науки нових шляхів удосконалення навчально-виховного процесу. „Освіта ХХІ століття – це освіта для людини”, - зазначено в Концепції 12-річної загальноосвітньої школи. «Пріоритетним напрямком оновлення змісту навчально-виховного процесу є гуманізація освіти, що базується на гуманістичних цінностях» (53, 47). Ось чому авторитарно–дисциплінарні моделі навчання змінюються на «особистісно-орієнтовані, суттєвими ознаками яких є навчання і виховання особистості з урахуванням усіх індивідуальних та фізіологічних процесів, які протікають в організмі дитини» (36, 19). Це створення умов для творчості, саморозвитку та самовиявлення особистості молодшого школяра.

Особистісне зорієнтоване навчання і виховання є перспективним, оскільки воно виходить із самостійності особистості, її духовності і суверенності. Його метою є формування людини як неповторної особистості, творця самого себе і своїх обставин. Сучасна школа матиме справу з індивідуальністю, самобутністю особистості, оскільки індивідуальність виявляється головним принципом етики і мусить вступати керівним методологічним положенням у вихованні і навчанні.

У системі загальної середньої освіти одне із основних місць займає початкова школа, де закладається фундамент розумових, моральних та емоційно-вольових якостей особистості. Курс математики початкових класів є основою для осмисленого засвоєння математичних знань, формування умінь і навичок, а також і отримання математичної освіти в цілому (55, 103).

Важливу роль у курсі математики початкової школи відіграють задачі. Вони, з одного боку, складають специфічний розділ програми, зміст якого учні мають засвоїти, з другого – виступають як дидактичний засіб навчання, виховання і розвитку школярів.

До проблеми розв’язування задач при вивченні математики тією чи іншою мірою зверталися відомі методисти. Психологічний та методичний аспект процесу розв’язування задач досліджували: Г.О. Балл, Л.Л. Гурова, С.Д. Максименко, Н.О. Менчинська, Н.А. Побірченко, З.І. Слєпкань, Л.М. Фрідман. Психолого-педагогічні і методичні основи диференційо-ваного навчання розкрито у працях М.І. Бурди, Ю.З. Гільбуха, О.С. Дубинчук, С.О. Логачевської, О.Л. Савченко, І.Є. Унт та ін.

Особливу увагу розв’язуванню задач як засобу розвитку мислення, формування системи математичних понять, добору задач до підручників з математики у початковій школі приділяли М.О. Бантова, Г.В. Бельтюкова, М.В. Богданович, М.М. Левшин, М.Г. Моро, Я.А. Король, Л.П. Кочіна, А.С. Пчолко, Н. Уткіна та ін.

Серед системи задач, які є предметом вивчення у початковому курсі математики, важливе місце займають задачі на пропорційне ділення. Розв’язування задач на пропорційне ділення «спрямоване на формування в учнів системи математичних знань, вироблення вмінь і навичок математичного моделювання, обчислення, розвитку прийомів розумової діяльності» (15, 71). Задачі на пропорційне ділення «допомагають розкрити опосередковані зв’язки математики з навколишнім середовищем і практичною діяльністю людей, реалізувати пізнавальні й виховні функції навчання» (52, 43). Процес розв’язування таких задач сприяє формуванню таких розумових дій як аналіз і синтез, конкретизація і абстрагування, порівняння, узагальнення тощо, а також розвитку функціонального мислення в цілому. Від оволодіння вміннями розв’язати задачі залежить не лише підготовка школярів з математики на даному етапі навчання, а й осмислення засвоєння систематичних курсів алгебри, геометрії, фізики, інформатики у наступних класах.

Позитивно оцінюючи наукову і практичну значущість досліджень з даної проблеми, необхідно, разом з цим, відзначити, що ряд аспектів формування вмінь розв’язувати задачі на пропорційне ділення залишилися нерозкриті, зокрема – обсяг теоретичних знань про таку задачу і процес її розв’язування у початкових класах; визначення рівнів програмних вимог до вироблення вмінь учнів початкової школи розв’язувати задачі на пропорційне ділення; добір різнорівневих завдань, спрямованих на формування вмінь розв’язувати задачі; способи раціонального поєднання фронтальної, групової та індивідуальної форми роботи на уроках математики при розв’язуванні задач на пропорційне ділення.

Отже, актуальність теми зумовлена значущістю досліджуваної проблеми для удосконалення методики розв’язування задач на пропорційне ділення у початковій школі, яка враховує особливості навчальної діяльності учнів під час розв’язування таких задач, психолого-педагогічні засади вироблення вмінь розв’язувати задачі на пропорційне ділення, різнорівневі вимоги до математичної підготовки школярів.

Об’єкт дослідження – процес навчання математики у початковій школі.

Предмет дослідження – формування вмінь учнів початкових класів розв’язувати задачі на пропорційне ділення.

Мета дослідження – проаналізувати, теоретично обґрунтувати і експериментально перевірити добірку задач на пропорційне ділення на уроках математики у початковій школі.

Гіпотеза дослідження: якщо, навчаючи розв‘язуванню задач на пропорційне ділення, враховувати зміст і операційний склад відповідних умінь, рівні програмових вимог до їх формування, психолого-педагогічні характеристики молодших школярів, дидактичні принципи добору завдань, то це підвищить ефективність навчання учнів розв’язувати задачі даного типу, а отже, рівень математичного розвитку школярів загалом.

Завдання дослідження:

- на основі аналізу психологічної і навчально-методичної літератури, практики навчання з’ясувати стан досліджуваної проблеми;

- розкрити зміст і операційний склад умінь учнів розв’язувати задачі на пропорційне ділення;

- визначити особливості навчальної діяльності учнів початкової школи під час розв’язування задач на пропорційне ділення;

- з’ясувати обсяг теоретичних знань про такий тип задач і процес їх розв’язування;

- розробити добірку завдань, спрямованих на вироблення вмінь розв’язувати задачі на пропорційне ділення;

- теоретично обґрунтувати та експериментально перевірити удосконалену методику формування вмінь розв’язувати задачі на пропорційне ділення.

Методи дослідження.

1. Теоретичні – системний аналіз психологічної і навчально-методичної літератури з проблеми дослідження (розкриття змісту, вмінь і закономірностей їх формування); семантичний аналіз задач на пропорційне ділення (з’ясування структурних компонентів задачі і зв’язків між ними); моделювання педагогічних ситуацій, аналіз та обробка результатів педагогічного експерименту (підтвердження ефективності експериментальної методики);

2. Емпіричні – спостереження, анкетування, тестування, бесіди з учнями і вчителями, вивчення досвіду вчителів, узагальнення власного досвіду викладання математики; формуючий експеримент.

Структура дослідження. Дипломна робота складається із таких основних елементів: вступ, два розділи, висновки, список використаної літератури, додатки.

РОЗДІЛ 1. ЗАГАЛЬНІ ПИТАННЯ НАВЧАННЯ РОЗВ’ЯЗУВАННЯ ЗАДАЧ

1.1 Система арифметичних задач у програмі з математики в початковій школі

Основним засобом, який використовується при вивченні математики для формування знань, умінь і навичок учнів, є задачі. Задачі являються засобом реалізації загальноосвітньої, виховної і розвиваючої цілей. Для формування виділених елементів теоретичних знань і оволодіння учнями відповідними їх видами діяльності необхідно розглядати систему задач, що забезпечує засвоєння навчального матеріалу.

За останні роки в педагогічній психології, дидактиці й методиці навчання математики були проведені дослідження з різних проблем теорії задачі. Значний внесок зробили: Н.Г. Амнєєв, Г.О. Балл, М.І. Бурда, Л.Л. Гурова, В.В. Давидов, О.М. Матюшкін та багато інших (5, 149-150). У цих дослідженнях вирішуються кардинальні питання постановки задач, їх структури, методики навчання розв’язання задач, зв’язків з відомим в умовах, коли суб’єкт не має способу (алгоритму) цієї дії.

На думку К.О. Славської, задача з психологічної точки зору – це не тільки об’єктивна вихідна ситуація, а насамперед задача, що виникає для людини, тобто об’єктивна вихідна проблемна ситуація, об’єктивне вихідне співвідношення умов і вимоги, що створює невідповідність між ними. Задачу мають розглядати як особливу форму пізнання дійсності. Тому вона сама виступає як об’єкт, що детермінує процес мислення людини.

Якщо аналізувати психологічний аспект розв’язування задач, то дослідники відмічають тісний зв'язок цього процесу з мисленням особистості (49, 74). Усі компоненти мислення (змістовий, операційний та процесуальний) виявляються в мисленнєвій діяльності особистості. Ця діяльність виникає і формується як процес за умов проблемної ситуації і задачі. Первинно виникає проблемна ситуація, тобто конфлікт, суперечність між обставинами та умовами – між наявними знаннями і актуальним потребами. Це малоусвідомлений процес невизначеності: “Що не так? Що не таке?” тощо.

Усвідомлення проблемної ситуації становить уже перший етап у її розв'язанні. На другому етапі відбувається вирізнення відомого і невідомого. Внаслідок цього проблемна ситуація перетворюється на задачу (40, 76). У структурі задачі вирізняють умову та вимоги. Для характеристики умови використовують такі ознаки, як звичність-незвичність ситуації, а також характер поставленої умови (словесний опис, зображення, реальна ситуація) і ступінь вираження в ситуації суттєвого відношення між відомими і невідомими величинами, що є ключовим у розв'язанні задачі.

Задачі мають задум (ідею, зміст). Важливою характеристикою вимог є чіткість їх формулювання. Задачу характеризує також співвідношення між умовами і вимогами. В умові можуть міститися всі елементи; необхідні для розв'язання задачі, можуть бути зайві елементи тощо.

Прикладом нашого підходу до поняття задачі є трактування, що його дав О.Ф. Єсаулов. Він пише: “Задача – це більш-менш визначені системи інформаційних процесів, неузгоджене або навіть суперечливе відношення між якими викликає потребу в їхньому перетворенні. Суть розв’язання саме і полягає у пошуках подолання шляхів такої неузгодженості” (1, 42).

Р.Е. Басангова визначає задачу як “як об’єкт розумової діяльності, що містить вимогу деякого практичного перетворення або відповіді на теоретичне питання за допомогою пошуку умов, що дозволяють розкрити зв’язки (відношення) між відомими і невідомими її елементами”.

З методичної точки зору поняття “задача” розглядається в роботах М.І. Бурди, Ю.М. Колягіна, В.І. Крупіча, Г.І. Саранцева й ін.

П.І. Сорокін під задачею розуміє об’єкт розумової діяльності, що містить вимогу і деякі умови, за яких, ця вимога має бути досягнута. Отже, задача повинна мати такі ознаки: бути носієм знань і умінь, а також засобом їх засвоєння; способом організації і керування пізнавальною діяльністю учнів; однією з форм прояву методів навчання; засобом зв’язку теорії з практикою (56, 13).

Задачі є і предметом і засобом навчання. Вони є основним засобом забезпечення зв'язку навчання із життям, політехнічного направлення в навчанні, здійснення міжпредметних зв'язків всередині математики і останньої з іншими навчальними предметами. На уроках математики навчальний процес в більшості випадків слідує від задач до теорії, а потім від теорії до задач: задачі => теорія => задачі.

Формування умінь розв’язувати задачі – одне із головних і складних завдань програми шкільного курсу математики в початкових класах (3). Складність цього завдання зумовлена багатьма факторами. Однак найбільш суттєвим є той, що в методиці навчання математики в початковій ланці освіти залишилися нереалізованими такі загально дидактичні принципи, як-от: науковості, послідовності, систематичності, зв’язку теорії з практикою, індивідуального підходу та ін.

Так, ще Я.А. Коменський зазначав, що міцно засвоюється лише те, що добре обґрунтовано. Отже, розв’язання тієї чи іншої задачі має бути науково обґрунтованим. Для цього учні повинні знати найелементарнішу класифікацію задач і вміти визначити, до якого саме виду належить та чи інша задача (26, 6).

Задача – це «сформульоване запитання, відповідь на яке можна знайти за допомогою арифметичних дій» (20, 28). З визначення задачі випливає, що в ній обов’язково має міститись якесь запитання. Без запитання задачі немає. Оскільки відповідь на запитання задачі дістаємо в результаті виконання арифметичних дій, очевидно, в ній повинна міститися вимога визначити те чи інше число (або числа) – шукане і, крім того, повинні вказуватися ті числа, за допомогою дій над якими можна знайти шукане. Тому обов’язковими елементами будь-якої арифметичної задачі є невідоме (шукане) число (чи кілька таких) і дані числа.

Головна особливість задач полягає в тому, що в них не зазначається, яку саме дію треба виконати над даними числами, щоб дістати шукане. Тому в тексті задачі потрібні непрямі вказівки на той зв’язок, який існує між даними числами і шуканими і який визначає добір потрібних арифметичних дій та їх послідовності. Це – умова задачі (7, 23). Умова, яка покликана розкрити зв’язки між даними і шуканими числами – містить числові і дані задачі.

Учні, як правило, досить легко засвоюють, що в задачі має бути не менше від двох числових даних. Діти часто підміняють задачу формулюванням умови і наслідку, який з неї випливає. Наприклад, складають такі “задачі”: “На гілці сиділо 3 пташки. До них прилетіла ще 1 пташка. Всього стало 4 пташки” (56, 14).

Отже, головні елементи задачі – умова і запитання. Числові (чи буквені) дані – це елементи умови. Шукане завжди міститься в запитанні. Але іноді задачу сформульовано так, що запитання містить у собі частину умови або вся задача викладена у формі запитання.

В навчанні математиці виділяють найбільш важливі функції задач: навчальні, виховні, розвиваючі, контролюючі (8, 287-188).

Навчальні функції спрямовані на формування у школярів системи математичних знань, умінь і навичок (як передбачених програмою, так і таких, що розширяють, поглиблюють її зміст) на різних етапах навчання.

Виховні функції спрямовані на формування пізнавального інтересу,самостійності, навичок навчальної праці, культури математичної мови, графічної культури.

Розвиваючі функції спрямовані на розвиток мислення в учнів, просторових уявлень, на оволодіння ними ефективними прийомами розумової діяльності.

Контролюючі функції спрямовані на встановлення рівня навчання, здібності до самостійного вивчення матеріалу, рівня математичного розвитку учнів і сформованості пізнавальних інтересів.

У зв'язку з великою кількістю видів математичних задач розглянемо існуючі їх класифікації. Зокрема, у методичній літературі (1; 4; 7; 9; 20; 35 та ін.) можна знайти наступні класифікації.

1. За кількістю невідомих у структурі задач. Ю.М. Колягін пропонує їх класифікувати на навчальні, пошукові та проблемні.

2. За характером об'єктів задачі поділяють на практичні та математичні.

3. За відношенням до теорії виділяють стандартні та нестандартні задачі. У ролі основної ознаки стандартних задач вказано наявність у курсі математики таких загальних правил і положень, що однозначно визначають програму розв'язання цих задач та виконання кожного кроку цієї програми (тобто мають свій алгоритм розв'язування). Нестандартні задачі - це такі, для яких у курсі математики не існує загальних правил або положень, що визначають точну програму їх розв'язання.

4. За функціями у процесі навчання розрізняють дидактичні, пізнавальні та розвиваючі задачі. Задачі з дидактичними функціями використовують для підготовки учнів до введення нового матеріалу, а також при його закріпленні: вони несуть функцію застосування теорії, що вивчається. Задачі з пізнавальними функціями мають за мету відпрацювати та поглибити основний зміст математичної дисципліни. Задачі з розвиваючими функціями – це ті, розв'язування яких потребує певних знань та вмінь, не передбачених програмою. Саме ці задачі спрямовані на розвиток мислення.

5. Задачі, що стимулюють навчально-пізнавальну діяльність; організують та здійснюють навчально-пізнавальну діяльність учнів; задачі, у процесі виконання яких здійснюється контроль та самоконтроль ефективності навчально-пізнавальної діяльності.

6. Задачі для початкової школи класифікують за змістом: задачі на рух, задачі на пропорційне ділення, на знаходження четвертого пропорційного.

7. За характером вимоги у початковому курсі математики виділяють задачі на обчислення, задачі на побудову, задачі текстові, задачі комбінованого характеру.

Наведені класифікації дозволяють ширше уявити собі проблеми, пов'язані з методикою навчання молодших школярів розв'язувати задачі, спрямовуючи цей процес на розвиток мислення.

Загалом задачі у початковому курсі математики класифікують на прості і складені. При цьому до простих належать 25 видів задач (на розкриття змісту арифметичних дій; на розкриття відношень між числами; задачі, що розкривають зв’язки між компонентами і результатами арифметичних дій; задачі на збільшення (або зменшення) числа на кілька одиниць ( чи в кілька разів) та ін.) (3, 106-107).

Прості задачі часто використовуються початковому курсі математики і при ознайомленні учнів з іншими сюжетами задач у справі формування в дітей уявлень про величини, їх вимірювання, про зв’язки, які існують між такими величинами, як ціна, кількість і вартість; маса одного предмета, число предметів і загальна маса; швидкість, час і пройдений шлях; довжина і ширина прямокутника та його площа; норма виробітку за одиницю часу, затрачений час і загальний виробіток, норма витрати яких-небудь матеріалів на один виріб, число виробів і загальна витрата матеріалів на них тощо (17, 3). Такі задачі розглядаються в 1-4 класах поступово, в міру розширення кола величин, що вводяться у зв’язку з вивченням відповідних питань і на матеріалі інших вправ.

Аналогічно до того, як прості задачі використовуються для створення наочної опори при розгляді таких питань теорії, як, скажімо, зв’язок між компонентами і результатами дії, значна група складених задач допомагає дітям усвідомити властивості розглядуваних дій. Це задачі, які ілюструють властивості додавання і віднімання, що вивчаються в I класі, а також властивості множення й ділення, розглядувані в II – IV класах.

Складені задачі, як і прості, використовуються і під час ознайомлення з деякими новими поняттями, новими випадками дій, вони допомагають дітям усвідомити нові для них поняття дробу числа й інші питання курсу (23, 51).

Складені арифметичні задачі відіграють важливу роль у навчанні дітей тих загальних прийомів розумової діяльності, які необхідні для розв’язання будь-якої задачі:

а) аналізувати, виділити відоме і невідоме;

б) встановлювати зв’язки між даними і шуканим;

в) складати план розв’язування;

г) перекладати залежності між даними і шуканим, сформульовані в задачі словами, на мову математичних виразів, рівностей, рівнянь;

д) виконувати відповідні дії (розв’язувати відповідні рівняння) і знаходити відповідь на запитання задачі;

е) перевіряти розв’язання (51, 32).

Складені задачі використовують як наочну конкретну основу для розгляду нових понять, властивостей дій. Цією функцією визначається й місце їх у загальній системі курсу: вони вводяться тоді, коли розглядаються відповідні питання, і в такій кількості, яка потрібна для пояснення нових питань. При цьому спеціальної мети навчити дітей розв’язувати задачі двома способами не ставиться. Важливіше, щоб вони могли розв’язати її раціональним способом.

Інша група складених задач, що займають велике місце в підручниках для початкових класів школи, пов’язана з роботою над різними кількісними відношеннями. Такі задачі вводяться після того, як діти достатньо засвоять кількісні відношення і навчаться застосовувати свої знання під час розв’язування простих задач, які містять слова “на стільки-то (у стільки-то разів) більше (менше)” в різному контексті.

Складені задачі дають можливість продовжити і розширити та поглибити роботу, спрямовану на ознайомлення дітей з різними величинами і залежністю між ними (62, 23).

Група складених задач, пов’язаних з необхідністю застосувати знання зв’язку між такими величинами, як ціна, кількість, вартість, займає важливе місце в підручниках для всіх чотирьох класів. Спеціальна увага приділяється задачам, які розкривають зв’язки між цими величинами в I – IV класах (35, 4).

У IIІ класі вводиться ряд нових величин (норма витрачання матеріалу на виріб, число виробів, загальна витрата матеріалу; норма виробітку за одиницю часу, витрачений час і загальний виробіток); у IV класі діти ознайомлюються із зв’язками між швидкістю, часом і відстанню при рівномірному русі, із зв’язком між сторонами прямокутника і його площею. Усі ці нові питання розглядаються не лише на основі практичних робіт, пов’язаних із спостереженнями, вимірюваннями, а й на матеріалі розв’язування різноманітних сюжетних задач, що показують, для яких практичних питань потрібні здобуті знання, вивчені взаємозв’язки між величинами.

Складені задачі поділяють за кількістю дій, якою розв’язується та чи інша задача. Це задача на дві, три, чотири дії. Трьома діями розв’язуються задачі, які утворилися розширенням задач на дві дії; також до цього типу належать також задачі на знаходження суми двох добутків, різниці двох добутків, різниці двох часток і т. ін. (51, 87).

Метою роботи над задачами є не тільки засвоєння способів їх розв'язування, а головним чином формування умінь, необхідних для самостійного розв'язування задач програмного мінімуму та подальшого навчання. У підручниках для 1—4 класів є такі задачі, які традиційно називають типовими, а також задачі з конкретним змістом. До типових належать задачі на знаходження четвертого пропорційного (на спосіб прямого і оберненого зведення до одиниці та спосіб відношень), на пропорційне ділення, на знаходження числа за двома різницями, на знаходження середнього арифметичного. Методика розв'язування типових задач принципово не відрізняється від розгляду будь-яких інших задач нового виду, тобто включає підготовку, ознайомлення і розвиток умінь (7, 29). Проте деякі особливості роботи над типовими задачами необхідно враховувати.

Зазначені типові задачі пов'язані з пропорційними величинами. Розв'язування їх ґрунтується на знанні відповідних зв'язків між величинами. Ознайомлення з величинами провадиться одночасно з розкриттям зв'язків між ними. Зв'язки формулюються у вигляді висновків. Наприклад, якщо відомо ціну і кількість, то вартість можна знайти дією множення. Типові задачі мають деякі характерні ознаки, які враховуються на підготовчому етапі роботи. Необхідно також враховувати взаємозв'язки між окремими типовими задачами. Особливу увагу слід приділити задачам на знаходження четвертого пропорційного до трьох даних.

Розв'язування задач на знаходження четвертого пропорційного способом зведення до одиниці запроваджується в 3 класі. Розгляду задач передує тривала робота над їх розв'язуванням на визначення ціни, кількості та вартості. Вона проводиться у вигляді гри "в магазин" (8). Під час гри учні вчаться розв'язувати задачі на знаходження вартості. ціни і кількості. Характерною особливістю в цій роботі є те, що, аналізуючи задачі, вчитель вимагає від учнів пояснення, які величини відомі і які треба знайти.

Розв'язування задач на знаходження середнього арифметичного ґрунтується на правилі: щоб знайти середнє арифметичне кількох чисел, треба їх суму поділити на кількість цих чисел. Це правило вводиться на основі аналізу готового розв'язання задачі.

Ознайомлення дітей із задачами на пропорційне ділення проводять у 4 класі. Спочатку вони виконують підготовчі завдання (7, 31).

У початковому курсі математики арифметичні задачі використовуються протягом усіх чотирьох років початкового навчання. Система їх розміщення, природно, збігається з логікою розгортання понять, що вводяться, ознайомлення з арифметичними діями і їх властивостями тощо. Особливість задач, які для цього відбираються, максимальна їх простота. Вони мають бути цілком зрозумілі, близькі дітям за сюжетом, просто викладені, без будь-яких незрозумілих, нових для дітей слів, які б потребували додаткових пояснень. Саме цій меті підпорядкована більша частина задач, широко представлених у програмі і в підручниках для кожного року навчання.

Оскільки в 1 класі діти вперше ознайомлюються з діями додавання і віднімання, а в 2 з діями множення і ділення, то тут передбачається використання простих текстових задач, насамперед спрямованих на розкриття змісту цих дій. Жодного означення дій у початкових класах не вводиться, і тому їх зміст діти мають усвідомити, головним чином, на основі практичних операцій з різними множинами предметів і в процесі розв’язування відповідних простих сюжетних задач, що дають змогу перевести ці операції в план розумових дій (39, 134).

Отже, добір і розміщення текстових задач для 1-4 класів підлягає логіці розгляду нових питань арифметичної теорії і відповідає вимозі поступового ускладнення завдань, що зумовлюється деякими особливостями форми подання математичних зв’язків і відношень, які визначають вибір арифметичної дії, необхідної для розв’язування задачі. Ускладнювати завдання можна, ввівши нові величини, розглядаючи з дітьми нові для них зв’язки.

Однією з функцій складених задач є розвиток здобутих знань, удосконалення їх у процесі застосування в змінених умовах. Але складені сюжетні задачі, введено в початковий курс математики не лише для цього. Одна з їх функцій – навчити дітей “перекладу” словесно заданих відношень і зв’язків між різними величинами, числами, на мову математичних виразів, рівностей, рівнянь. Цій меті підпорядковані і добір задач, і система їх розміщення в часі, і методика роботи над ними.

Ця система забезпечує поступовий перехід від простого до дедалі складнішого: від складання простих виразів і рівнянь у процесі розв’язання задач на одну дію до складання виразів з 2-3 діями при розв’язуванні досить легких за структурою складених задач. Поступове наростання труднощів у таких вправах можливе тільки тоді, коли вчитель розуміючи завдання, що стоять перед ним, використовуватиме для цього пропоновані вправи з підручника (23, 54).

Лише вчитель може визначити, яку задачу і коли можна запропонувати дітям, яке завдання доцільно пов’язати з розв’язуванням цієї задачі: в одному разі досить вказати дію, за допомогою якої розв’язується задача, в іншому – скласти за нею вираз чи рівняння, ще в іншому – доцільно розібрати хід розв’язування за діями, послідовно з’ясовуючи роль кожної з них і коментуючи здобуті результати.

Отже, серед типових складених задач важливе місце займають задачі на пропорційне ділення. Саме цей вид задач є предметом нашого дослідження.

1.2 Ступені роботи над текстовими задачами

Розв'язати математичну задачу – це значить знайти таку послідовність загальних положень математики (означень, аксіом, теорем, правил, законів, формул), використовуючи які до умов задачі чи до їх наслідків (проміжних результатів розв'язання), одержуємо те, що вимагається в задачі, - її відповідь.

Вченими обґрунтовано, що психологічною основою формування вмінь розв’язувати текстові задачі є основні положення теорії поетапного формування розумових дій (О.М. Леонтьєв, П.Я. Гальперін, Н.Ф. Тализіна та ін.) у синтезі з основними положеннями асоціативно-рефлекторної теорії (Д.Н. Богоявленський, Є.Н. Кабанова-Меллер, Н.О. Менчинська та ін.). Уміння розв’язувати текстові задачі виробляються ефективно, якщо:

1) подавати повну орієнтовну основу дій;

2) при первинному поясненні розгорнуто подавати зразок розв’язування задачі з фіксацією складових операцій;

3) опрацьовувати виконання окремих дій, які входять до складу загального вміння шляхом розв’язання спеціальних вправ;

4) використовувати різні види моделей задачної ситуації;

5) забезпечувати різні види діяльності (репродуктивну, продуктивну, творчу) та тривалість процесу формування вміння (4, 43).

Робота над задачами не повинна зводитись до формування навичок розв’язування задач спочатку одного виду, потім другого і т. д. Основна мета – навчити дітей свідомо встановлювати певні зв’язки між даними і шуканим у різних життєвих ситуаціях, передбачаючи поступове ускладнення їх. Щоб добитися цього, вчитель повинен передбачити в методиці навчання розв’язування задач одного виду різні ступені, які мають свою мету.

На першому ступені вчитель готує дітей до розв’язування задач розглядуваного виду. На цьому ступені учні повинні засвоїти зв’язки, на основі яких вони вибиратимуть дії в процесі розв’язування таких задач.

На другому ступені вчитель ознайомлює учнів з розв’язуванням задач розглядуваного виду. Тут учні навчаються встановлювати зв’язки між даними і шуканим і на цій основі вибирати арифметичні дії, тобто вони навчаються переходити від конкретної ситуації, вираженої в задачі, до вибору відповідної арифметичної дії. Внаслідок такої роботи учні ознайомлюються з способом розв’язування задач цього виду.

На третьому ступені вчитель закріплює вміння розв’язувати задачі розглядуваного виду. На цьому ступені учні мають навчитися розв’язувати будь-яку задачу розглядуваного виду незалежно від її конкретного змісту, тобто вони мають узагальнити спосіб розв’язування задач цього виду (29, 19-20).

Узагальнено структура процесу розв’язування задач подана на рис.

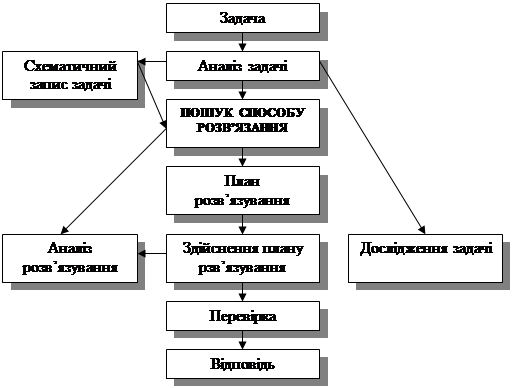Рис. Структура процесу розв’язування задачі

Розглянемо докладніше методику роботи на кожному з названих ступенів (8, 213-214).

Підготовча робота до розв’язування задач того чи іншого виду (перший ступінь) залежить від того, на який зв’язок між даними і шуканим треба спиратися під час вибору арифметичних дій. Відповідно до цього виконують спеціальні вправи.

1. Перед розв’язуванням задач у багатьох випадках виконують операції над множинами. Під час ознайомлення з розв’язуванням більшості простих задач повинні виконуватись вправи на оперування множинами. Елементами множин мають бути конкретні предмети (палички, геометричні фігури вирізані з паперу, самі учні, рисунки тощо.). Наприклад, до введення простих задач на знаходження суми пропонують вправи на об’єднання множин.

Дістаньте картинки, де намальовані курчата. (Діти виконують). На подвір’ї було 3 курчат. До них прибігли ще 2 курчат. Скільки тепер курчат? (Діти лічать картинки). Ми до 3 додали 2 (показує на картинки) і дістали 5.

Підготовкою до розв’язування задач на віднімання буде виконання операції вилучення частини певної множини, на множення – виконуються операції об’єднання рівно чисельних множин, на ділення – поділ множин на рід рівно чисельних множин.

За допомогою операції над множинами розкривають зміст виразів “більше на...”, “менше на...”, “більше в кілька разів...”, “менше в кілька разів...”, що є підготовкою для введення задач, пов’язаних з поняттям різниці та кратного відношення.

2. Більшість арифметичних задач пов’язана з величинами (довжина, час, маса, місткість тощо), тому треба ознайомити дітей із цією величиною. Також дітям корисно для подальшої роботи записувати в окремі зошити чи блокноти значення деяких величин: ціни на окремі товари, швидкості різних видів транспорту, відстані між містами чи найближчими селищами тощо.

3. Арифметичні дії під час розв’язування багатьох задач вибирають на основі зв’язків, які існують між величинами. Щоб у процесі вибору дій діти використовували і усвідомлювали ці зв’язки, потрібно розкрити зв’язки між величинами, розв’язуючи задачі на основі їх конкретного змісту.

Щоб учні засвоїли той чи інший зв’язок, треба організувати цілеспрямовані спостереження. Щоб розкрити зв’язок між ціною, кількістю і вартістю, доцільно організувати екскурсію в магазин, де учні ознайомляться з ціною, запишуть ціни на деякі товари в свої довідники і будуть спостерігати процес купівлі-продажу. Потім на уроці діти складуть ряд простих задач на знаходження вартості за відомою ціною і кількістю, розв’яжуть їх, опираючись на знання конкретного змісту дії множення. Розглянувши розв’язування, учні помітять, що коли відомо ціну і кількість, то вартість знаходять дією множення.

4. Розв’язування складених задач зводиться до розв’язування ряду простих, тому підготовкою до розв’язування складених задач буде навчання розв’язування простих задач.

Розгляду кожного окремого виду задач має передувати спеціальна підготовча робота. Провівши відповідну підготовчу роботу, можна перейти до ознайомлення дітей з розв’язуванням задач розглядуваного виду (20, 28).

У методиці початкового навчання математики виділяють такі етапи розв'язування задач, як ознайомлення із змістом задачі, аналіз задачі і відшукання плану розв'язування, розв'язання задачі та перевірка розв'язування. Розглянемо методику роботи на кожному з цих етапів.

1. Ознайомлення із змістом задачі. Усвідомлення змісту задачі — необхідна умова її розв'язання. Учень не повинен приступати до розв'язування задачі, не зрозумівши її умови. Тому ознайомлення з задачею містить власне опанування її змісту і перевірки усвідомлення його дітьми.

Учень ознайомлюється з задачею із слів учителя або самостійно. Це, так би мовити, «крайні способи». Поряд з ними використовуються «проміжні способи», в яких ступінь самостійності учнів залежить від рівня їхньої підготовленості і мети розв'язування задачі. Приступаючи до розв'язування задачі, важливо сприйняти її в цілому, а потім вже розбивати на окремі частини (22, 26).

При фронтальному ознайомленні вчитель читає (або переказує) задачу двічі. Першого разу задачу читають з метою ознайомлення з її змістом в цілому. Другого разу задачу читають частинами і так, щоб кожна частина містила певну смислову «одиницю» тексту. Поділ задачі на частини здебільшого передбачає виділення окремих числових даних її. Під час другого читання доцільно на дошці записувати умову. Читаючи задачу, вчитель паузами та інтонацією виділяє числові дані та слова, що визначають вибір дії та запитання задачі. Емоційне забарвлення голосу допомагає учням уявити ту життєву ситуацію, про яку йдеться в задачі. Тому, слухаючи задачу, дітям не варто слідкувати очима за текстом підручника. Якщо в задачі є маловідомі дітям терміни, то їх слід пояснити заздалегідь, застосовуючи для цього предметне ілюстрування або малюнки.

Щоб перевірити, як учні усвідомили умову задачі, вчитель задає учням запитання (за смислом окремих частин) або пропонує переказати всю задачу. З метою активізації контрольного повторення задачі слід наперед ставити перед учнями те або інше завдання. Наприклад: «Послухайте задачу і повторіть вголос її запитання», «Прочитайте задачу самостійно і скажіть, що нам відомої про...». (7, 42)

Розглянуті вимоги стосуються і самостійного читання задач учнями. Діти повинні засвоїти, що в процесі, читання треба запам'ятати або виписати числові дані і виділити запитання задачі і найбільш важливі слова, які стосуються даних і шуканого чисел, а також з'ясувати незрозумілі слова.

2. Аналіз задачі і відшукання плану її розв'язування. Учень зможе успішно розв'язати задачу, якщо розу