Методы статистических исследований
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ПРАВА И ФИНАНСОВ
КОНТРОЛЬНАЯ РАБОТА
По курсу: «Статистика»
Выполнил: студент группы ПФ-176\з
Исаенко В.В.
Проверил: Земцова Е.М.
Челябинск
2008
Задача 1
Для изучения выполнения плана рабочими завода было проведено десятипроцентное выборочное обследование по методу случайного бесповторного отбора. Результаты обследования показали следующее распределение рабочих по проценту выполнения норм выработки:
| Выполнение норм, % | Число рабочих, чел. |
| До 90 | 4 |
| 90-100 | 16 |
| 100-110 | 40 |
| 110-120 | 30 |
| 120-130 | 10 |
| ИТОГО: |
На основании этих данных вычислить:
1) средний процент выполнения нормы;
2) моду и медиану;
3) размах вариаций;
4) среднее линейное отклонение;
5) дисперсию;
6) среднее квадратичное отклонение;
7) коэффициент вариации, оцените однородность совокупности;
8) с вероятностью 0,954 возможные пределы, в которых ожидается средний процент выполнения норм выработки по заводу;
9) с вероятностью 0,954 возможные пределы доли рабочих, выполняющих нормы выработки более, чем на 110%.
Сделать выводы.
Решение:
Перед нами представлен ряд с равными интервалами. Интервал равен 10. И один отрытый интервал «до 90». Так как следующий за открытым интервал равен 10 следовательно при расчетах получим границу верхнего интервала, она будет равна «80-90».
1) Найдем середины интервалов по формуле:
![]()
Получаем следующие значения: 85, 95, 105, 115, 125.
Используя среднюю арифметическую взвешенную, определим средний процент выполнения нормы:![]()
![]()
![]() Средний процент выполнения нормы равен 107,6%.
Средний процент выполнения нормы равен 107,6%.
2)Рассчитаем моду:
![]() = 100+10
= 100+10![]()
Таким образом, наиболее часто встречающееся значение процента выполнения нормы равно 107,06%
Рассчитаем медиану:

Подставляем значения:
![]() - нижняя граница медианного интервала «100-110», равная 100;
- нижняя граница медианного интервала «100-110», равная 100;
![]() - величина медианного интервала, равная 10:
- величина медианного интервала, равная 10:
![]() - накопленная частота интервала, предшествующая медианному, равная 20:
- накопленная частота интервала, предшествующая медианному, равная 20:
| Выполнение норм, % | Число рабочих, чел. | Накопленная частота |
| До 90 | 4 | 4 |
| 90-100 | 16 | 4+16=20 |
| 100-110 | 40 | 20+40=60 |
| 110-120 | 30 | 60+30=90 |
| 120-130 | 10 | 90+10=100 |
| ИТОГО: | 100 | - |
![]() полусумма частот, равная 50:
полусумма частот, равная 50:
![]() соответственно полусумма равна 50;
соответственно полусумма равна 50;
![]() - частота медианного интервала, равная 40.
- частота медианного интервала, равная 40.

3) Рассчитаем размах вариаций - разность между самым большим и самым малым наблюдаемыми значениями признака:
R=Xmax – Xmin = 130-80 = 50
4) Рассчитаем среднее линейное отклонение ![]() . Эта величина определяется как средняя арифметическая из абсолютных значений отклонений
. Эта величина определяется как средняя арифметическая из абсолютных значений отклонений ![]() и
и ![]() . Так как сумма отклонений значений признака от средней величины равна нулю, то все отклонения берутся по модулю.
. Так как сумма отклонений значений признака от средней величины равна нулю, то все отклонения берутся по модулю.
Формула среднего линейного отклонения для нашего случая:

Найдем середину интервалов, определим произведения значений середины интервалов на соответствующие им веса и подсчитаем сумму их произведений, рассчитаем абсолютные отклонения середины интервалов от средней велечины, вычислим произведения отклонений на их веса и подсчитаем сумму их произведений.
Средняя величина нами рассчитана в первом пункте задания и равна![]()
Выполнение норм, %
| Число рабочих, чел.
| Середина интервала
|
|
|
|
| А | 1 | 2 | 3 | 4 | 5 |
| До 90 | 4 | 85 | 340 | 22,6 | 90,4 |
| 90-100 | 16 | 95 | 1520 | 12,6 | 201,6 |
| 100-110 | 40 | 105 | 4200 | 2,6 | 104 |
| 110-120 | 30 | 115 | 3450 | 7,4 | 222 |
| 120-130 | 10 | 125 | 1250 | 17,4 | 174 |
| ИТОГО: | 100 | - | 10760 | - | 792 |
Рассчитываем среднее линейное отклонение:

Таково в среднем отклонение вариантов признака от их средней величины. Это отклонение по сравнению со средней величиной признака небольшое. Оно отличается от средней на 99,68%. Это свидетельствует о том, что данная совокупность в отношении нашего признака однородна, а средняя – типична.
5) Дисперсия есть не что иное, как средний квадрат отклонений индивидуальных значений признака от его средней величины.
Формула дисперсии для нашего случая:

Рассчитаем данные и заполним таблицу:
| Выполнение норм, % | Число рабочих, чел. | Середина интервала |
|
|
|
| А | 1 | 2 | 3 | 4 | 5 |
| До 90 | 4 | 85 | 340 | 510,76 | 2043,04 |
| 90-100 | 16 | 95 | 1520 | 158,76 | 2540,16 |
| 100-110 | 40 | 105 | 4200 | 6,76 | 270,4 |
| 110-120 | 30 | 115 | 3450 | 54,76 | 1642,8 |
| 120-130 | 10 | 125 | 1250 | 302,76 | 3027,6 |
| ИТОГО: | 100 | - | 10760 | - | 9524 |

6)Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются конкретные варианты признака от среднего значения и равно корню квадратному из дисперсии:

Степень вариации в данной совокупности невелика, так как средняя величина выполнения нормы равна 107,6%. Это говорит об однородности рассматриваемой совокупности.
7) коэффициент вариации, оцените однородность совокупности:
![]()
Так как коэффициент вариации в нашем примере меньше 33% совокупность считается однородной.
8) вычислить с вероятностью 0,954 возможные пределы, в которых ожидается средний процент выполнения норм выработки по заводу.
Для определения заданных пределов нам необходимо рассчитать предельную ошибку выборки по формуле:
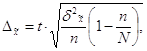 где:
где:
t – коэффициент доверия, для нашего случая равен 2;
![]() - выборочная дисперсия;
- выборочная дисперсия;
N – численность генеральной совокупности, так как наша выборка десятипроцентная, то N = 1000;
n – численность выборки.

Определим заданные пределы по формуле:
![]()
или ![]()
С вероятностью 0,954 можно утверждать, что средний процент выполнения норм выработки по заводу будет находиться в пределах от 105,75% до 109,45%.
9) с вероятностью 0,954 возможные пределы доли рабочих, выполняющих нормы выработки более, чем на 110%
Согласно результатам обследования, численность таких рабочих составила 40 человек, определим выборочную долю:
![]()
Внутригрупповая дисперсия доли определяется по формуле:
![]()
Предельная ошибка выборки с заданной вероятностью составит:

Определим границы пределов:
![]()
или ![]()
Следовательно, с вероятностью 0,954 можно утверждать, что для рабочих, выполняющих нормы выработки более, чем на 110% находится в пределах от 0,307 до 0,493%.
Задача 2
Себестоимость продукции завода характеризуется следующими данными:
| Изделия | Себестоимость единицы продукции, тыс. руб. | Выработано продукции, тыс. единиц | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| К-220 | 12 | 10 | 0,9 | 1,2 |
| СР-1 | 8 | 7 | 6,4 | 9,3 |
| З-322 | 12 | 10 | 15 | 15,2 |
Для завода по трем видам изделий вместе определите:
1) общий индекс затрат на продукцию;
2) общий индекс себестоимости продукции;
3) общий индекс физического объема продукции;
4) выполните факторный анализ;
Покажите взаимосвязь между индексами (а, б, в).
Решение:
Для выполнения расчетов заполним таблицу:
| Изделия | Себестоимость единицы продукции, тыс. руб. | Выработано продукции, тыс. единиц | Затраты на продукцию, млн. руб. | |||
| базисный период | отчетный период | базисный период | отчетный период | базисный период | отчетный период | |
z0 | z1 | q0 | q1 | q0z0 | q1z1 | |
| К-220 | 12 | 10 | 0.9 | 1.2 | 10,8 | 12 |
| СР-1 | 8 | 7 | 6.4 | 9.3 | 51,2 | 65,1 |
| З-322 | 12 | 10 | 15 | 15.2 | 180 | 152 |
| Итого: | 32 | 27 | 242 | 229,1 | ||
1) общий индекс затрат на продукцию:
![]()
2) общий индекс себестоимости продукции:
![]()
3) общий индекс физического объема продукции:
![]()
4) факторный анализ:
Изменение затрат на продукцию ∆zq = ∑z1q1 - ∑z0q0 = 229,1-242 = -12,9 млн. руб.
Влияние фактора себестоимости 1 шт. ∆z = ∑z1q1 - ∑z0q1 = 229,1 – 271,2 = -42,1 млн. руб.
Влияние фактора объема продукции ∆q = ∆zq - ∆z = -12,9 – (- 42,1) = 29,2 млн. руб.
Между индексами а, б и в существует следующая взаимосвязь:
Izq = Iz * Iq = 0.845*1.121=0.947
Задача 3
Динамика средних цен и объема продажи продукта на колхозных рынках 2-х городов характеризуется следующими данными:
| Города | Средняя цена 1 кг., руб. | Продано продукта, тыс. кг. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| p0 | p1 | q0 | q1 | |
| А | 1,2 | 1,8 | 200 | 225 |
| Б | 1,5 | 1,4 | 220 | 190 |
Вычислите:
1) Индекс цен переменного состава;
2) Индекс цен постоянного состава;
3) Индекс цен структурных сдвигов;
4) Изменение средней себестоимости (в абсолютных величинах) в целом и за счет действий отдельных факторов.
Покажите взаимосвязь исчисленных индексов.
Решение:
Индекс цен переменного состава рассчитывается по формуле:

![]()
Индекс цен постоянного состава рассчитывается по формуле:

![]()
Индекс структурных сдвигов рассчитывается по формуле:

![]()
Покажем взаимосвязь индексов:

![]()
Средняя себестоимость выросла на 19,1%. За счет структурных сдвигов себестоимость увеличилась на 58,1%. Если бы структура реализации продукта по городам не изменилась, средняя себестоимость увеличилась бы на 20,9 %.
Задача 4
| Отрасли | Стоимость товарной продукции, млрд. руб. | Фондоотдача, руб. | Стоимость ОФ, руб. | |||
| базисный период | отчетный период | базисный период | отчетный период | базисный период | отчетный период | |
| Тяжелая промышленность | 584,9 | 609,9 | 0,84 | 0,84 | 696,30 | 726,07 |
| Легкая промышленность | 119,8 | 120,9 | 4,19 | 4,08 | 28,59 | 29,63 |
| Итого: | 704,7 | 730,8 | 5,03 | 4,92 | 724,9 | 755,7 |
Провести анализ динамики и факторов изменения фондоотдачи в целом по промышленности.
Решение:
1) Рассчитаем стоимость ОФ и заполним таблицу.
2) Фондоотдача в среднем по промышленности:


3) Для изучения динамики изменения фондоотдачи:
а) найдем индекс переменного состава
![]()
б) найдем индекс фиксированного состава
![]() , где
, где
![]() доля стоимости основных фондов каждой отрасли в общем объеме отчетного периода
доля стоимости основных фондов каждой отрасли в общем объеме отчетного периода
![]()
![]()
![]()
![]()
в) Индекс структурных сдвигов
![]()
4) Факторный анализ
Общее снижение фоноотдачи
![]()
В том числе за счет фактороф изменения фондоотдачи в каждой отрасли
![]()
Структурных сдвигов в составе основных фондов
![]()
Вывод: средняя фондоотдача в целом по промышленности снизилась в 0.995 раз. За счет изменения фондоотдачи в каждой отрасли средняя фондоотдача снизилась в 0.996 раз. За счет изменения структуры основных фондов средняя фондоотдача снизилась в 0.999.
Задача 5
| Показатели | База | Отчет |
| Выручка от реализации продукции в действовавших ценах | 3240 | 3960 |
| Средний годовой остаток оборотных средств | 540 | 594 |
Определить изменение скорости оборотных средств (дней) в отчетном периоде по сравнению с базисным и сумму средств высвобожденных из оборота вследствие ускорения оборачиваемости. Сделать выводы.
Решение:
Рассчитаем продолжительность одного оборота по формуле:
![]() дн.
дн.
![]() дн.
дн.
Скорость оборота оборотных средств в отчетном периоде по сравнению с базисным увеличилась на 54-60=-6дн.
Сумма средств высвобожденных из оборота вследствие ускорения оборачиваемости:
![]()
Вывод: скорость оборота оборотных средств в отчетном периоде по сравнению с базисным увеличилась на 6 дней и привела к высвобождению из оборота 66 у.е средств.
Задача 6
Выплавка стали характеризуется следующими показателями:
| Годы | Производство электроэнергии, млрд. кВт-ч. |
| 1 | 91,0 |
| 2 | 96,9 |
| 3 | 102,2 |
| 4 | 106,5 |
| 5 | 110,3 |
| 6 | 116,0 |
| 7 | 119,6 |
| 8 | 125,3 |
| 9 | 130,8 |
| 10 | 136,0 |
| 11 | 139,8 |
| 12 | 145,2 |
Для анализа ряда динамики исчислите:
1) показатели, характеризующие рост выплавки стали: абсолютные приросты, темпы роста и прироста (по годам и к базисному году). Результаты расчетов изложите в табличной форме;
2) средний уровень и среднегодовой темп ряда динамики;
3) покажите взаимосвязь между цепными и базисными показателями;
4) для определения основной тенденции ряда произведите выравнивание ряда динамики с помощью укрупнения интервалов.
Изобразите фактический и выровненный динамические ряды на графике.
Сделайте выводы.
Решение:
1) показатели, характеризующие рост выплавки стали: абсолютные приросты, темпы роста и прироста (по годам и к базисному году).
| Годы | Производство электроэнергии | Абсолютный прирост (∆у) | Темп роста, % (Тр) | Темп прироста, % (Тп) | |||
цепной способ ∆уi = уi – уi-1 | к базисному (первому) году ∆уi = уi - уб | цепной способ Тр = уi / уi-1 * 100 | к базисному (первому) году Тр = уi / уб * 100 | цепной способ Тп = Тр – 1 | к базисному (первому) году Тп = Тр – 1 | ||
| 1 | 91 | - | - | - | - | - | - |
| 2 | 96,9 | 5,9 | 5,9 | 106,48 | 106,48 | 6,48 | 6,48 |
| 3 | 102,2 | 5,3 | 11,2 | 105,47 | 112,31 | 5,47 | 12,31 |
| 4 | 106,5 | 4,3 | 15,5 | 104,21 | 117,03 | 4,21 | 17,03 |
| 5 | 110,3 | 3,8 | 19,3 | 103,57 | 121,21 | 3,57 | 21,21 |
| 6 | 116 | 5,7 | 25 | 105,17 | 127,47 | 5,17 | 27,47 |
| 7 | 119,6 | 3,6 | 28,6 | 103,1 | 131,43 | 3,1 | 31,43 |
| 8 | 125,3 | 5,7 | 34,3 | 104,77 | 137,69 | 4,77 | 37,69 |
| 9 | 130,8 | 5,5 | 39,8 | 104,39 | 143,74 | 4,39 | 43,74 |
| 10 | 136 | 5,2 | 45 | 103,98 | 149,45 | 3,98 | 49,45 |
| 11 | 139,8 | 3,8 | 48,8 | 102,79 | 153,63 | 2,79 | 53,63 |
| 12 | 145,2 | 5,4 | 54,2 | 103,86 | 159,56 | 3,86 | 59,56 |
2) Средний уровень ряда уср = (у1+у2+у3+у4+у5+у6+y7+y8+y9+y10+y11+y12) / 12 = (91+96,9+102,2+106,5+110,3+ 116+119,6+125,3+130,8+136+139,8+145,2) / 12 = 118.3.
Средний темп роста ряда динамики определяется по формуле

или 104,3%
Средний темп прироста рассчитывается по формуле:
![]()
3) взаимосвязь между цепными и базисными показателями
а) ![]()
т.е. ![]()
б) ![]()
4) Выравнивание ряда динамики с помощью укрупнения интервалов проведем с помощью трехчленной скользящей средней.
![]()
![]() 96.7, 101.9, 106.3, 110.9, 115.3, 120.3, 125.2, 130.7, 135.5, 140.3.
96.7, 101.9, 106.3, 110.9, 115.3, 120.3, 125.2, 130.7, 135.5, 140.3.
Первую скользящую среднюю отнесем ко второму году, десятую отнесем к одиннадцатому году.

В результате укрупнения интервалов общая тенденция роста выступает отчетливо. В среднем ежегодно выплавлялось стали 101,4 млн.т. Каждый год объем выплавки увеличивался в среднем на 4.3%.
Задача 7
В отчетном периоде работа 24 предприятий характеризуется следующими данными:
Данные о работе предприятий в отчетном периоде
| Заводы, П/П | Продукция в сопоставимых ценах, млрд. руб. | Стоимость основных производственных фондов, млрд. руб. | |
| 1 | 0,9 | 0,9 | |
| 2 | 2,6 | 2,5 | |
| 3 | 5,5 | 5,6 | |
| 4 | 4,1 | 4 | |
| 5 | 4,9 | 4,8 | |
| 6 | 0,9 | 1 | |
| 7 | 1,3 | 1,2 | |
| 8 | 6,4 | 5,2 | |
| 9 | 2,8 | 2,5 | |
| 10 | 0,8 | 0,9 | |
| 11 | 0,7 | 0,7 | |
| 12 | 4,9 | 3,9 | |
| 13 | 12,1 | 10,6 | |
| 14 | 12,2 | 11,7 | |
| 15 | 11,8 | 10,7 | |
| 16 | 8,5 | 6,1 | |
| 17 | 7,1 | 7,3 | |
| 18 | 2,9 | 4,1 | |
| 19 | 14 | 10,7 | |
| 20 | 4,8 | 7,3 | |
| 21 | 15,7 | 12,5 | |
| 22 | 11,8 | 8,4 | |
| 23 | 16,6 | 12,7 | |
| 24 | 10,2 | 7,8 | |
| Итого: | 163,5 | 143,1 |
С целью выявления зависимости между стоимостью основных производственных фондов и выпуском продукции произведите группировку заводов по размеру основных фондов, образовав 6 групп заводов с равными интервалами. Результаты представьте в групповой таблице. Сделайте краткие выводы.
Итоговая таблица
| № группы | Группы заводов по размеру ОПФ (интервалы) млн.руб. | Число заводов | Стоимость ОПФ | Стоимость валовой продукции млн.руб. | Фондоотдача | ||
| Всего | В среднем на один завод | Всего | В среднем на один завод | ||||
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
| 5 | |||||||
| 6 | |||||||
| ИТОГО | |||||||
Исследуйте зависимость между стоимостью продукции (результативный признак – у) и стоимостью основных производственных фондов (факторный признак – х). На основании исходных данных:
1) постройте поля корреляции; составьте корреляционную таблицу, определив число интервалов по правилу Стерджесса; нанесите эмпирическую линию регрессии на поле корреляции и сделайте выводы о возможной форме связи;
2) в целях синтезирования моделей зависимости задайте вид и вычислите параметры уравнения связи, нанесите полученную теоретическую линию регрессии на график;
3) для установления практической значимости полученной модели вычислите возможные показатели тесноты связи (коэффициент детерминации, эмпирическое и теоретическое корреляционные отношения, линейный коэффициент корреляции);
4) оцените надежность полученных коэффициентов, сделайте выводы по п.п. 2, 3 и 4.
5) используя полученную модель, сделайте прогноз стоимости продукции для предприятия со стоимостью основных фондов 14 млрд.рублей.
Решение:
1) Величина интервала i = (xmax –xmin)/n = (12700 – 700) / 6 = 2000 млн. руб.
Фондоотдача = Стоимость валовой продукции / Стоимость ОПФ.
| № группы | Группы заводов по размеру ОПФ (интервалы) млн.руб. | Число заводов | Стоимость ОПФ | Стоимость валовой продукции млн.руб. | Фондоотдача | ||
| Всего | В среднем на один завод | Всего | В среднем на один завод | ||||
| 1 | 700-2700 | 7 | 9700 | 1385,71 | 10000 | 1428,57 | 1,03 |
| 2 | 2700-4700 | 3 | 12000 | 4000 | 11900 | 3966,67 | 0,99 |
| 3 | 4700-6700 | 4 | 21700 | 5425 | 25300 | 6325 | 1,17 |
| 4 | 6700-8700 | 4 | 30800 | 7700 | 33900 | 8475 | 1,1 |
| 5 | 8700-10700 | 3 | 32000 | 10666,67 | 37900 | 12633,33 | 1,18 |
| 6 | 10700-12700 | 3 | 36900 | 12300 | 44500 | 14833,33 | 1,21 |
| ИТОГО | 24 | 143100 | 5962,5 | 163500 | 6812,5 | 6,68 | |
Вывод: Между стоимостью ОПФ и валовой продукцией прямая связь, с ростом ОПФ растет и валовая продукция.
Построим поле корреляции по исходным данным задачи.

Составим корреляционную таблицу, определив число интервалов по правилу Стерджесса n = 1 + 3,322 lg24 = 6.
Корреляционная таблица зависимости между стоимостью продукции (у) и стоимостью основных производственных фондов (х)
 ;
; ![]()
| i | Величина ОПФ, млрд. руб. | Середина интервала | Продукция в сопоставимых ценах, млрд. руб. | Всего nxi | Групповая средняя yj | |||||
| 0,7-3,35 | 3,35-6,0 | 6,0-8,65 | 8,65-11,3 | 11,3-13,95 | 13,95-16,6 | |||||
xi yj | 2,025 | 4,675 | 7,325 | 9,975 | 12,625 | 15,275 | ||||
| 1 | 0,7-2,7 | 1,7 | 7 | - | - | - | - | - | 7 | 2,025 |
| 2 | 2,7-4,7 | 3,7 | 1 | 2 | - | - | - | - | 3 | 3,79 |
| 3 | 4,7-6,7 | 5,7 | - | 2 | 2 | - | - | - | 4 | 6 |
| 4 | 6,7-8,7 | 7,7 | - | 1 | 1 | 1 | 1 | - | 4 | 8,65 |
| 5 | 8,7-10,7 | 9,7 | - | - | - | - | 2 | 1 | 3 | 13,51 |
| 6 | 10,7-12,7 | 11,7 | - | - | - | - | 1 | 2 | 3 | 14,39 |
Всего nyj | 8 | 5 | 3 | 1 | 4 | 3 | 24 | |||
Групповая средняя xj | 1,95 | 5,3 | 6,37 | 7,7 | 9,7 | 11,0333 | ||||
По данным графика и корреляционной таблицы можно сделать вывод, что связь прямая.
2) Так как связь между признаками линейная:
![]()
Найдем ![]() и
и ![]() :
:

| Заводы, П/П | Стоимость основных производственных фондов, млрд. руб.(х) | Продукция в сопоставимых ценах, млрд. руб. (y) | x^2 | y^2 | xy | |
| 1 | 0,9 | 0,9 | 0,81 | 0,81 | 0,81 | |
| 2 | 2,5 | 2,6 | 6,25 | 6,76 | 6,5 | |
| 3 | 5,6 | 5,5 | 31,36 | 30,25 | 30,8 | |
| 4 | 4 | 4,1 | 16 | 16,81 | 16,4 | |
| 5 | 4,8 | 4,9 | 23,04 | 24,01 | 23,52 | |
| 6 | 1 | 0,9 | 1 | 0,81 | 0,9 | |
| 7 | 1,2 | 1,3 | 1,44 | 1,69 | 1,56 | |
| 8 | 5,2 | 6,4 | 27,04 | 40,96 | 33,28 | |
| 9 | 2,5 | 2,8 | 6,25 | 7,84 | 7 | |
| 10 | 0,9 | 0,8 | 0,81 | 0,64 | 0,72 | |
| 11 |
Подобные работы:
Актуально:
|