Случайные вектора
Случайные вектора
Оглавление
Функция распределения вероятностей двух случайных величин.. 2
Совместная плотность распределения вероятности двух случайных величин 4
Условная функция распределения вероятностей.. 7
Условная плотность вероятности.. 7
Числовые характеристики двумерного случайного вектора. 8
Верхняя и нижняя границы корреляции и ковариации.. 10
Ковариация и независимость двух случайных величин.. 11
Ковариация и геометрия линий равного уровня плотности вероятности 13
Коэффициент корреляции.. 15
Коэффициент корреляции и расстояние. 17
Функция распределения вероятностей случайного вектора. 18
Плотность вероятности случайного вектора. 19
Многомерное нормальное распределение. 21
Характеристическая функция случайного вектора. 22
Функции от случайных величин.. 23
Распределение вероятностей функции одной случайной величины.. 24
Преобразование нескольких случайных величин.. 28
Хи - квадрат распределение вероятностей.. 30
Хи - квадрат распределение и распределение Максвелла по скоростям.. 33
Литература. 35
Функция распределения вероятностей двух случайных величин
В задачах со случайным исходом обычно приходится учитывать взаимодействие нескольких случайных величин. Это естественным образом приводит к понятию многомерных (векторных) случайных величин или совокупности нескольких случайных величин. Случайный вектор является третьим основным объектом изучения теории вероятностей (после случайного события и случайной величины). Целесообразно начать изучение случайных векторов с рассмотрения двухмерных векторов, свойства которых сравнительно простые и наглядные.
Совместной функцией распределения вероятностей (или двумерной функцией распределения вероятностей) случайных величин 
, 
(или случайного вектора 
) называется функция
. (50.1)
Следует иметь в виду, что 
- вероятность события 
- пересечения двух событий: 
и 
. В записях вида (50.1) принято вместо символа 
использовать запятую.
50.1. Рассмотрим основные свойства функции 
, следующие из ее определения.
1). 
, где 
- функция распределения вероятностей случайной величины . Действительно, 
- достоверное событие, поэтому 
. Аналогично 
, где 
- функция распределения вероятностей случайной величины .
2). 
, поскольку события 
, - достоверные, следовательно их пересечение – достоверное событие и 
.
3). 
, поскольку событие 
- невозможное и 
. Аналогично 
.
4). - неубывающая функция аргумента 
, а также неубывающая функция аргумента 
.
5). непрерывна справа по каждому аргументу.
50.2. Рассмотрим геометрическую интерпретацию функции . Пусть случайные величины , являются компонентами случайного вектора . Тогда результат каждого опыта по измерению случайного вектора можно рассматривать как точку на плоскости, а функция 
определяет вероятность попадания точки в часть плоскости: 
, выделенной на рис. 50.1 штриховкой.
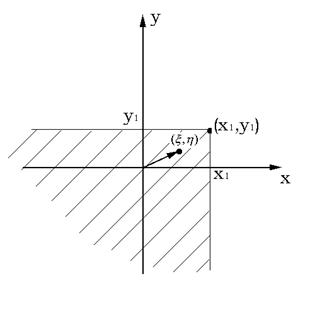
Рис. 50.1. Геометрическая интерпретация функции .
Представим вероятность 
- попадания случайного вектора в прямоугольник 
, 
, 
, 
, рис 50.2, через функцию . Несложно определить, что
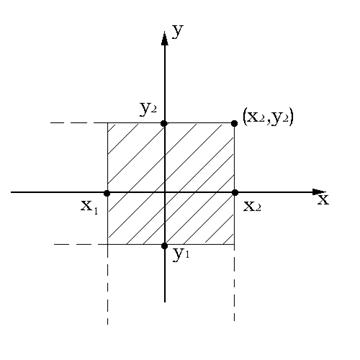
Рис. 50.2. К вычислению вероятности попадания в прямоугольник.
(50.2)
Пусть 
, 
- малые величины и функция имеет первые производные по и , а также вторую смешанную производную, тогда из (50.2) следует:
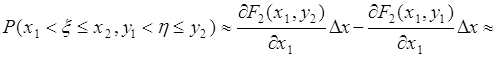
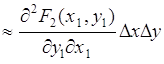. (50.3)
Отсюда:
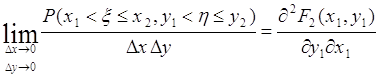. (50.4)
Совместная плотность распределения вероятности двух случайных величин
Пусть у функции 
существуют производные по , , а также вторая смешанная производная. Совместной (или двумерной) плотностью распределения вероятностей случайных величин и называется функция
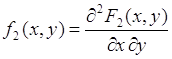(51.1)
Рассмотрим основные свойства двумерной плотности вероятности.
1. Справедливо соотношение:
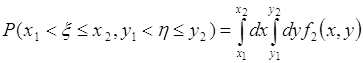. (51.2)
Для доказательства используем равенство (51.1), тогда:
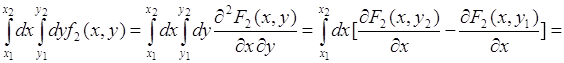
. (51.3)
Теперь из равенства (50.2) следует (51.2). Это соотношение имеет практическое значение, поскольку позволяет вычислять вероятность 
- попадания двумерного вектора 
в прямоугольник, определяемый отрезками 
и 
через плотность вероятности 
.
2. Рассмотрим частный случай соотношения (51.2). Пусть 
, 
, 
, 
, тогда (51.2) принимает вид:
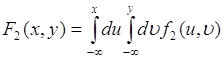. (51.4)
Это соотношение определяет функцию распределения вероятностей 
через плотность вероятности 
и является обратным по отношению к равенству (51.1).
3. Рассмотрим (51.2) при условиях: , 
, 
, 
, тогда из (51.2) следует равенство:
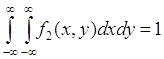, (51.5)
поскольку 
- как вероятность достоверного события. Соотношение (51.5) называется условием нормировки для плотности вероятности .
4. Если - плотность вероятности вектора , и 
- плотность вероятности случайной величины , то
. (51.6)
Это равенство называется свойством согласованности плотности второго порядка и плотности первого порядка . Если известна плотность второго порядка , то по формуле (51.6) можно вычислить плотность вероятности - случайной величины . Аналогично,
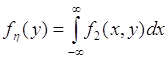. (51.7)
Доказательство (51.6) получим на основе равенства
. (51.8)
Представим через плотность согласно (51.4), а 
через , тогда из (51.8) следует
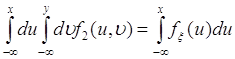. (51.9)
Дифференцирование (51.9) по приводит к равенству (51.6), что и завершает доказательство.
5. Случайные величины и называются независимыми, если независимы случайные события 
и 
при любых числах 
и 
. Для независимых случайных величин и :
. (51.10)
Доказательство следует из определений функций и , 
. Поскольку и - независимые случайные величины, то события вида: 
и 
- независимые для любых и . Поэтому
(51.11)
- справедливо равенство (51.10). Продифференцируем (51.10) по и , тогда согласно (51.1) получаем следствие для плотностей:
. (51.12)
6. Пусть 
- произвольная область на плоскости 
, тогда
(51.13)
- вероятность того, что вектор принимает любые значения из области определяется интегралом по от плотности вероятности .
Рассмотрим пример случайного вектора с равномерным распределением вероятностей, который имеет плотность вероятности 
на прямоугольнике 
и 
- вне этого прямоугольника. Число
определяется из условия нормировки:
.
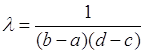Условная функция распределения вероятностей
Пусть случайные величины и имеют плотности вероятности 
и 
соответственно и совместную плотность 
. Рассмотрим равенство:
. (52.1)
Отсюда
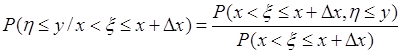(52.2)
Функция
(52.3)
называется условной функцией распределения вероятностей случайной величины при условии, что случайная величина принимает значение 
.
Подставим (52.2) в (52.3), тогда
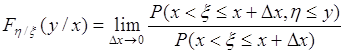. (52.4)
Представим вероятности в (52.4) через плотности вероятностей, тогда
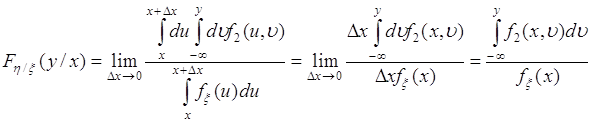(52.5)
Это соотношение определяет условную функцию 
через плотности и . Отметим, что для независимых случайных величин и совместная плотность 
. При этом, как следует из (52.5), условная функция 
- не зависит от аргумента (т.е. не зависит от событий вида 
.
Аналогично (52.3) можно определить функцию 
случайной величины при условии, что 
, и затем получить выражение аналогичное (52.5)
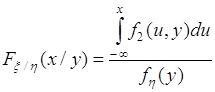. (52.6)
Условная плотность вероятности
Условной плотностью распределения вероятностей случайной величины при условии 
называется функция:
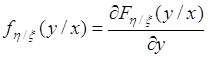. (53.1)
Соотношение (52.5) подставим в (53.1), тогда
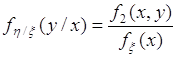. (53.2)
Отсюда следует
. (53.3)
- формула умножения для плотностей. Эта формула аналогична формуле умножения вероятностей. Очевидно,
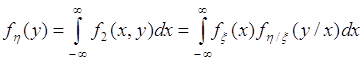. (53.4)
Данное равенство является аналогом формулы полной вероятности.
Аналогично (53.1) вводится условная плотность распределения вероятности случайной величины при условии как функция вида:
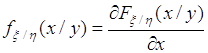. (53.5)
Отсюда и из (52.6) следуют соотношения:
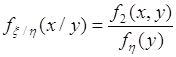, (53.6)
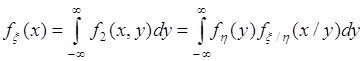. (53.7)
В (53.6) подставим (53.3) и (53.4), тогда:
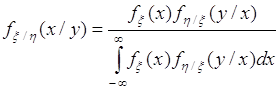. (53.8)
Это соотношение аналогично формуле Байеса. Здесь случайные величины и можно поменять местами, тогда получим также верное соотношение для условной плотности 
, которая определяется через функции и 
.
Числовые характеристики двумерного случайного вектора
54.1. Пусть случайные величины и имеют совместную плотность вероятности 
и 
- функция двух переменных. Тогда 
- случайная величина, полученная подстановкой случайных величин и вместо аргументов и .
Математическим ожиданием случайной величины называется число
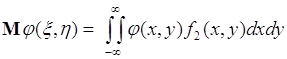. (54.1)
Если 
, 
, тогда из (54.1) следует
, 
, 
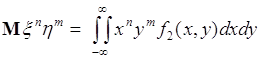. (54.2)
Числа 
называются начальными смешанными моментами порядка 
случайных величин и . Эти числа применяются в качестве статистических характеристик двумерного случайного вектора. Рассмотрим частные случаи (54.2). 1). 
, тогда 
- начальный момент порядка 
случайной величины . При дополнительном условии 
получаем 
- математическое ожидание случайной величины , при 
- 
- среднее ее квадрата и т.д. Таким образом, при смешанные моменты (54.2) совпадают с начальными моментами случайной величины . 2). Если положить 
, тогда 
- смешанные моменты совпадают с начальными моментами случайной величины . В обоих случаях получаем индивидуальные характеристики одной из случайных величин. 3). Для получения групповой характеристики (54.2), отражающей свойства совокупности двух случайных величин, необходимо рассмотреть ненулевые 
. Наиболее простой вариант: 
, . При этом из (54.2) следует
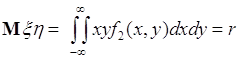. (54.3)
Число 
называется корреляцией случайных величин и и представляет собой важнейшую характеристику совокупности двух случайных величин.
Если и - независимы, то 
и (54.3) преобразуются следующим образом:
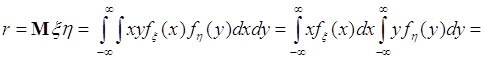
, (54.4)
где 
и 
. При этом выражается через индивидуальные характеристики 
и 
, т.е. каких-либо групповых эффектов в не проявляется, что является следствием независимости случайных величин и . Из цепочки преобразований (54.4) следует равенство 
- математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
54.2. Аналогично (54.2) числа
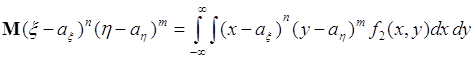(54.5)
называются центральными смешанными моментами, порядка . Наиболее важной групповой характеристикой двух случайных величин среди чисел (54.5) является ковариация
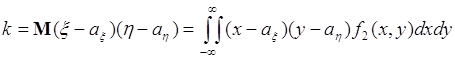, (54.6)
которая является центральным смешанным моментом порядка 
. Для ковариации используется также обозначение: 
. Если 
, то 
- совпадает с дисперсией случайной величины .
Если и - независимы, то из (54.6) следует, что ковариация
.
Обратное утверждение в общем случае неверно, т.е. из равенства 
в общем не следует независимость случайных величин и . В частности, обратное утверждение справедливо, если и - гауссовы случайные величины. Более подробно этот вопрос обсуждается ниже.
54.3. Найдем связь между корреляцией и ковариацией 
случайных величин и . Из определения ковариации (54.6) следует
.
Таким образом, ковариация и корреляция связаны соотношением
. (54.7)
Верхняя и нижняя границы корреляции и ковариации
55.1. Пусть случайные величины и имеют математические ожидания 
, , дисперсии 
, 
, корреляцию 
и ковариацию 
. Рассмотрим неравенство
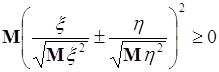. (55.1)
Возведем в квадрат, затем оператором математического ожидания подействуем на каждое слагаемое, тогда (55.1) принимает вид:
,
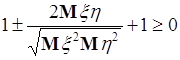что далее сводится к неравенству
. (55.2)
Его левая часть 
может быть как положительной так и отрицательной, правая часть - только положительна. Поэтому неравенство (55.2) обычно записывается в более сильном варианте:
. (55.3)
Таким образом, корреляция случайных величин и принимает значения из интервала 
.
Соотношение, аналогичное (55.3) можно получить и для ковариации , если в исходном выражении (55.1) вместо подставить центрированную случайную величину 
и вместо соответственно 
. При этом необязательно выполнять все преобразования, аналогичные (55.1) - (55.3), достаточно учесть, что замена 
и 
приводит к замене 
на 
, на 
, а также на . Поэтому из (55.3) следует
. (55.4)
55.2. Неравенства, определяющие область значений корреляции и ковариации , аналогичные (55.3), (55.4), можно получить в другом виде на основе следующего очевидного неравенства:
. (55.5)
Отсюда 
, поэтому справедливо неравенство
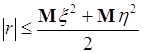. (55.6)
Если в (55.5) 
заменить соответственно на и , то в (55.6) заменяется на , 
на 
и 
на 
. Поэтому (55.6) принимает вид:
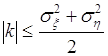. (55.7)
Ковариация и независимость двух случайных величин
Для независимых случайных величин и ковариация 
. В отличие от этого рассмотрим другой крайний случай, когда случайные величины и связаны функциональной зависимостью:
, (56.1)
где 
- числа. Вычислим ковариацию случайных величин и :
. (56.2)
Из (56.1) следует 
. Подставим этот результат в (56.2), тогда
. (56.3)
Из (56.1) определим дисперсию
, (56.4)
откуда 
. Это равенство подставим в (56.3), тогда
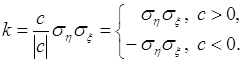(56.5)
Таким образом, ковариация линейно связанных случайных величин и принимает максимальное значение 
, если 
, или минимальное значение 
, если 
, на отрезке 
допустимых значений для в общем случае (согласно формуле (55.4)).
В связи с этим можно выдвинуть предположение о том, что ковариация является мерой статистической связи между случайными величинами и . Действительно, для двух крайних случаев получены подходящие для этого результаты, а именно: для независимых величин , а для линейно связанных 
максимален. Далее будет показано, что это предположение верно, но не в общем, а только для статистической связи линейного типа. Эта связь характерна тем, что при усилении этой связи растет , и в пределе связь вырождается в линейную зависимость (56.1).
Однако если связь имеет нелинейный характер, то величина не отражает меру (степень) этой связи. Рассмотрим следующий пример. Пусть 
, 
, и 
- случайная величина с равномерным на интервале 
распределением вероятностей. Случайные величины и связаны между собой соотношением: 
. Таким образом, между величинами и существует функциональная связь, а не статистическая, и следовало ожидать, что величина максимальна. Однако, прямые вычисления приводят к результату . Действительно,
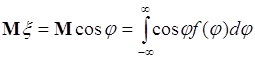, (56.6)
где
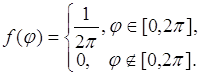
- плотность распределения вероятностей случайной величины . С учетом этого (56.6) преобразуется:
.
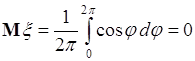Аналогично
,
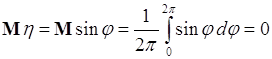теперь ковариация
.
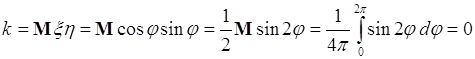Таким образом, для нелинейной связи между случайными величинами их ковариация не может использоваться как мера статистической связи, поскольку значение ковариации не отражает степень этой связи.
Ковариация и геометрия линий равного уровня плотности вероятности
Ковариация случайных величин и определяется через их совместную плотность вероятности 
соотношением:
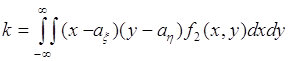. (57.1)
Подынтегральная функция в (57.1) неотрицательна для таких , , при которых 
, то есть при 
, 
или 
, 
. И наоборот, при , или , подынтегральная функция (57.1) отрицательна либо равна нулю. Знак ковариации зависит от того, какие значения, положительные или отрицательные преобладают в подынтегральной функции. Поэтому знак числа определяется расположением линий равного уровня плотности вероятности . На рис. 57.1 представлен пример линий равного уровня функции , для которой 
. Штриховкой
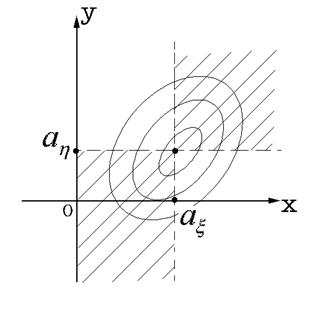
Рис. 57.1.
Линии равного уровня плотности вероятности при .указана часть плоскости, на которой 
, и следовательно неотрицательна подынтегральная функция. Поскольку в заштрихованной области (положительные значения подынтегральной функции) плотность имеет в среднем большее значение, чем в нештрихованной области (отрицательные значения подынтегральной функции), то ковариация 
. На рис. 57.2 представлены линии равного уровня плотности при 
. Случай соответствует симметричному расположению линий относительно прямой 
(или 
). Например, эти линии могут быть эллипсами, у которых большая полуось совпадает по направлению с прямой (или ). Другой пример – линии являются окружностями с центром в точке 
.
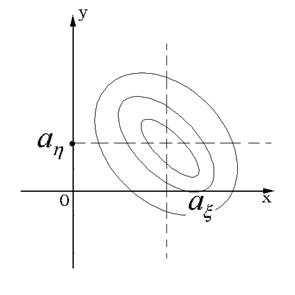
Рис. 57.2. Линии равного уровня плотности
вероятности при .
Отметим, что если 
, а линии равного уровня имеют ось симметрии, например, на рис. 57.1 линии – это эллипсы, тогда можно выполнить преобразование (вращение) системы координат 
, такое, что в новой системе ковариация . Это означает также и преобразование случайных величин , с ненулевой ковариацией к новым случайным величинам, для которых ковариация равна нулю.
Коэффициент корреляции
58.1. Коэффициентом корреляции двух случайных величин и называется число
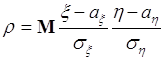. (58.1)
Коэффициент корреляции является ковариацией: 
двух безразмерных случайных величин
, 
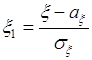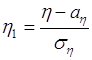, (58.2)
полученных из исходных величин и путем преобразования специального вида (58.2) (нормировки), которое обеспечивает нулевые средние 
, 
и единичные дисперсии 
, 
.
Коэффициент корреляции (58.1) можно представить через ковариацию случайных величин и :
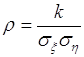. (58.3)
Поскольку 
, то из (58.3) следует
. (58.4)
Коэффициент корреляции является безразмерной величиной, принимает значения на интервале 
и поэтому используется как мера статистической связи линейного типа между случайными величинами и , в отличие от ковариации , для которой интервал значений 
зависит от дисперсий случайных величин. Рассмотрим примеры вычисления коэффициента корреляции, позволяющие выяснить свойства 
как меры статистической связи между случайными величинами.
58.2. Пусть - случайная величина с математическим ожиданием , дисперсией и 
. Ковариация случайных величин и определяется формулой (56.5): 
. Подставим это соотношение в (58.3) , тогда:
(58.4)
Таким образом, для случайных величин , , связанных линейной зависимостью коэффициент корреляции принимает либо максимальное значение 
, либо минимальное - 
.
58.3. Рассмотрим обобщение линейной функции, связывающей случайные величины и на линейную случайную функцию следующего вида:
(58.5)
где 
и - независимые случайные величины. В частном случае - число и (58.5) – линейная функция, определяющая через . Для детерминированной линейной связи 
- принимает максимальное значение. Если - случайная величина, то связь (58.5) становится статистической (стохастической, случайной), то есть не столь жесткой как детерминированная функциональная связь. Это приводит к 
. В зависимости от свойств случайной величины статистическая связь между и может быть сильной, 
, или слабой, 
. Для того, чтобы ответить на вопрос, какова мера связи между случайными величинами и (58.5) вычислим их коэффициент корреляции.
Пусть 
, 
, 
, 
. Тогда из (58.5) следует, в силу независимости и:
.
Выразим дисперсию случайные величины через параметры случайных величин ,:
. (58.6)
Теперь по фор