Проектирование металлической балочной конструкции
Федеральное агентство по образованию
Государственное образовательное учреждение высшего
профессионального образования
Кафедра: Строительных конструкций
Курсовой проект по дисциплине
"Металлические конструкции"
На тему: "Проектирование металлической балочной конструкции"
Выполнил: ст. гр. ПГС
Маковецкий А.О.
Проверил :
Тонков Л.Ю.
Пермь 2009
Содержание
1. Исходные данные
2. Компоновочное решение
3. Расчет и конструирование балок
3.1 Вспомогательные балки
3.1.1. Сбор нагрузок
3.1.2. Силовой расчет
3.1.3. Назначение типа сечения вспомогательных балок и марки стали
3.2 Главные балки
3.2.1 Силовой расчет
3.2.2 Компоновка сечения и проверка прочности и общей устойчивости
3.2.3 Изменение сечения главной балки
3.2.4 Проверка общей устойчивости и деформативности балок
3.2.5 Проверка местной устойчивости балок
3.2.6 Расчет поясных швов, опорных частей балок, узлов сопряжений балок
4. Расчет и конструирование колонн
4.1 Выбор расчетной схемы
4.2 Компоновка сечения колонны
4.3 Проверка сечения колонны
4.4 Конструирование и расчет оголовка колонны
4.5 Конструирование и расчет базы колонны
4.6 Подбор сечения связей по колоннам
Литература
1. Исходные данные
| Длинна пролета | L | 10.2 | м |
Длинна второстепенной балки | l | 6.2 | м |
| Высота колоны | Hк | 7.8 | м |
| Толщина плиты настила | tпл | 8 | см |
| Нагрузка | qн | 13 | кН/м2 |
Схема пролета
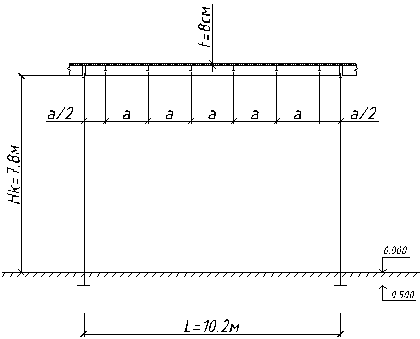
2. Компоновочное решение
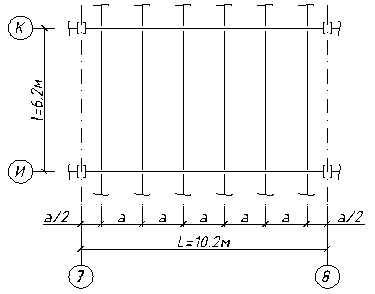
Проектирование сооружения начинаем с назначения компоновочной схемы, в которой за основу, принимаем балочную клетку нормального типа, опирающуюся на центрально-сжатые колонны. Устойчивость сооружения в плоскости главных балок обеспечивается путем примыкания этих балок к жесткому блоку (для рабочих площадок – это каркас здания цеха). В плоскости, перпендикулярной главным балкам, устойчивость сооружения обеспечивается путем постановки связей по колоннам, т.е. созданием диска.
3. Расчет и конструирование балок
3.1Вспомогательные балки
3.1.1Сбор нагрузок
Нагрузка на вспомогательные и все нижележащие конструкции состоит из постоянной составляющей и временной (полезной) нагрузки.
Сбор нагрузок на рабочую площадку:
| № п/п | Наименование нагрузки | Нормативная нагрузка, кН/м2 |
| Расчетная нагрузка, кН/м2 | ||
| Постоянная нагрузка | ||||||
| 1 | Пол асфальтобетонный: | 0.72 | 1.3 | 0.94 | ||
| t= | 40 | мм | ||||
| 18 | кН/м3 | ||||
| 2 | Монолитная ж/б плита: | 2.00 | 1.1 | 2.2 | ||
| t= | 8 | мм | ||||
| 25 | кН/м3 | ||||
| 3 | Собственный вес второстепенных балок: | 0,20 | 1.05 | 0.21 | ||
| Итого постоянная нагрузка q: | 2.92 | 3.35 | ||||
| 4 | Полезная нагрузка p: | 13 | 1.2 | 15.6 | ||
| Всего нагрузка (q+p): | 15.92 | 18.95 | ||||
3.1.2 Силовой расчет
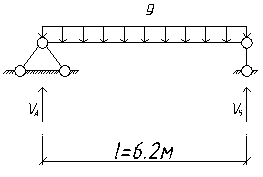
Погонная нагрузка на вспомогательные балки равна:
g = ( + q)·a = 18.95·1.7 = 32.215 кН/м.
Опорные реакции:
VA = VB = g·l/2 = 32.215·6.2 / 2 = 99.867 кН.
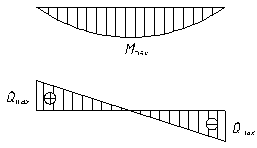
Максимальный изгибающий момент:
Mmax = g·l2/8 = 32.215·6.2² / 8 = 154.793 кНм.
Максимальная поперечная сила:
Qmax = VA = 99.867 кН.
3.1.3 Назначение типа сечения вспомогательных балок и марки стали
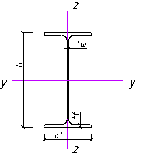
Сечение принимаем в виде стального горячекатаного двутавра с параллельными гранями полок по ГОСТ 26020-83.
Марка стали С255. Расчетное сопротивление марки стали Ry (по пределу текучести) принимаем по СНиПу II-23-81*: Ry = 240Мпа.
Сечение балок назначаем из условия прочности:
σ = Mmax·γn / C1·Wn,min£ Ry·γc, (3.1.1)
где Мmax – максимальный расчетный изгибающий момент в балке;
Wn,min – момент сопротивления сечения балки, т.е. требуемый Wтр;
γс – коэффициент условия работы балки, γc = 1 (СНиП II-23-81*);
γn– коэффициент надёжности, γn=0.95;
С1 – коэффициент, принимаем равный С1 = С = 1.12 (СНиП II-23-81*).
Из условия прочности (3.1.1) находим требуемый момент сопротивления:
Wтр = Мmax· γn / C1·Ry·γc, (3.1.2)
Wтр =154.793·103·0.95 / 1.12·240·106·1 = 547.073 см³.
Зная Wтр= 547.073 см³, подбираем по сортаменту СТО АСЧМ 20-93 Б, ближайший номер профиля с избытком, Wx > Wтр и выписываем из сортамента для него геометрические характеристики:
Двутавр 35 Б1:
Wy = 641.3 м³Wz = 91 м³
Iy = 11095 см4; Iz = 791.4 см4;
iy = 14.51 см; iz = 3.88 см;
Sy = 358.1 м³It = 13.523 см4;
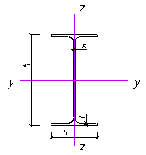
A = 52.68 см2
t = 9 мм;
= 174 мм;
h = 346 мм;
= 6 мм.
Проводим проверки прочности:
σ = Mmax· γn / C1·Wy£Ry· γc, (3.1.3)
где по СНиПу II-23-81*C1 = 1.09.
σ = 154.793·10³·0.95 / 641.3·10-6·1.09 = 210.4 МПа.
σ =210.4 МПа < Ry· γc= 240 МПa,
τ = Qmax·γn / hw·tw (3.1.4)
τ =99.867·10³·0.95 / 6·10-3·328·10-3 = 48.21 МПа.
проверка прочности выполняются.
Проверку деформативности балок производим от действия нормативных нагрузок и при равномерно распределенной нагрузке используем формулу:
ƒ/l = 5·gн·l3/384·E·Iy£ (ƒ/l), (3.1.5)
где l - пролет балки, равный l = 6.2 м;
gн = (pн + qн) · a = 27.064 кН/м;
Е = 2,06·105МПа;
(ƒ/l) - нормируемый относительный прогиб балки,
принимаем по СНиПу II-23-81*: (ƒ/l) = 1/200.556.
ƒ/l = 5·27.064·103·6.23/384·2.06•106·11095·10-6 = 6.375·10-3.
ƒ/l = 6.375·10-3 < (ƒ/l)= 4.986·10-3,
проверка деформативности выполняется.
Проверка общей устойчивости балок производится по формуле:
σ = Mmax· γn /φb·Wy£Ry· γc, (3.1.6)
Wy – принятый момент сопротивления балки;
γс = 0.95 при проверке устойчивости;
φb – коэффициент, определяемый по СНиПу II-23-81*.
Определяем φb, находим по формулe:
φ1 = ψ·Iz/Iy·(h/lef)²·E/Ry(3.1.7)
где h – высота сечения балки;
ψ – коэффициент, определяем по формуле:
ψ = 1,6 + 0.08·α(3.1.8)
α = 1.54·It/ Iz·(lef/h)²(3.1.9)
α = 1.54·13.523/791.4·(6.2/0.346)2 = 8.449;
ψ = 1.6+0.08∙8.449 = 2.276;
φ1 = 2.276·791.4/11095·(0.346/6.2)2·2.06·105/240 = 0.434;
φ1 < 0.85 → φb = φ1
σ= 154.793·103·0.95/641.3·10-6·0.434 = 528.4 МПа
Проверка общей устойчивости не выполняется. В связи с тем, что настил ж/б устойчивость обеспечится.
3.2 Главные балки
3.2.1 Силовой расчет
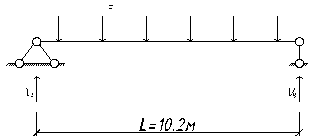
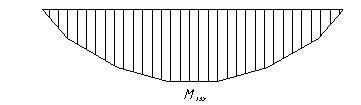
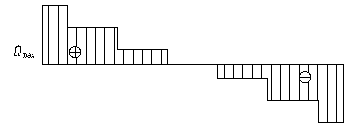
F=2·Rв.б.·α = 2·99.867·1.05 = 209.721 кН;
VA = VB = 30.6·F / L = 30.6·209.721 / 10.2 = 629.763 кН
Mmax = 5.1· VA - 7.65·F= 5.1·629.163 – 7.65·209.721 = 1604.366 кНм
Qmax = VA = 629.763 кН.
3.2.2 Компоновка сечения и проверка прочности и общей устойчивости
Главные балки проектируются сварными составного сечения. Тип сечения – симметричный двутавр. Компоновка сечения начинается с назначения высоты балки 'h'. В нашем случае высота балки назначается исходя из двух критериев:
1. Из условия экономичности.
2. Из условия жесткости балки.
Исходя, из условия минимального расхода стали, высота балки определяется при h ≤ 1.3 по формуле:
hопт = k·ÖWт р/ tw, (3.2.1)
где h– высота балки, определяется в первом приближении как h≈ 0.1•L, h≈1.02<1.3 м;
L– пролет главной балки;
к = 1.15 – для балок постоянного сечения;
γс = 1.
Wтр = Mmax·γn / Ry·γc, (3.2.2)
Wтр = 1604.366·103·0.95 / 240·106·1 = 6351 см³,
tw = (7 + 3· (h,м)), 3.2.3)
tw = 7 + 3·1.02 = 10.06 мм, округляем кратно 2 мм: tw = 12 мм,
hопт = 1.15·Ö6351 / 1.2 = 83.662 cм < 1.3 м.
Из условия обеспечения требуемой жесткости:
hmin = 5·Ry·γc·L· (L/ƒ) ·(н+ qн) / (24·E·( + q) ·γn), (3.2.4)
где по СНиПу II-23-81*:(L/ƒ) = 1/211.667,
hmin = 5·240·106·1·10.2·211.667·15.92 / (24·2.06·106·18.95·0.95) = 47.7 см.
Из полученных высот hопт, hmin принимаем большую h = hопт = 83.662 см, следуя рекомендациям при h< 1м – принимаем h кратную 5 см, т.е. h = 85 см. Минимально допустимая толщина стенки из условия прочности на срез определяется по формуле:
tw(min)³ 1.5·Qрасч·γn/ hef·Rs·γc, (3.2.5)
где Rs– расчетное сопротивление стали сдвигу в зависимости от значения Ry:
Rs = 0.58·Ry;
Rs = 0.58·240·106 = 139.2 МПа;
hef – расчетная высота стенки, равная hef = 0.97·h.
hef = 0.97∙85=82 см;
tw(min) ³ 1.5·629.163·103·0.95 / 0.82·139.2·106 = 7.86 мм.
Т.к. tw(min)> 6 мм, то согласно сортаменту, толщиной кратной 2 мм., принимаем толщину стенки tw = 8 мм.
Повторяем вычисления:
hопт = 1.15·Ö6351 / 0,8 = 102.465 cм > 1 мокругляем кратно 10 см → h=110 см
tw(min) ³ 1.5·629.163·103·0.95 / 1.1·139.2·106 = 6.036 мм> 6 мм → tw= 8 мм.
Для определения значений bf, tf необходимо найти требуемую площадь пояса Аf по формуле:
Af = 2·(Iy – Iw)/h², (3.2.6)
где Iy – требуемый момент инерции, определяемый по формуле:
Iy = Wтр·h/2, (3.2.7)
Iw – момент инерции стенки сечения, определяемый по формуле:
Iw = tw·hef3/12, (3.2.8)
Iy= 6351·110/2 = 349300 см4,
Iw = 0.8·106.7³/12 = 80980 см4,
получаем:
Af = 2·(349300 – 80980)/110² = 44.35 см².
Ширину пояса выбираем из условия:
bf = (1/3 - 1/5) ·h, (3.2.9)
tf = Af/bf, (3.2.10)
bf и tf назначаем с учетом сортамента на листовую сталь, при этом должно выполняться условие:
bf/tf < |bf/tf| »ÖE/Ry. (3.2.11)
bf = (1/3 - 1/5)·110 = 289.5 мм, округляем кратно 20 мм → bf = 300 мм
тогда
tf= 44.35/30 = 1.49 см, округляем кратно 2 мм → tf = 16 мм
В соответствии с сортаментом и расчетом принимаем следующие величины по ГОСТ 82-70: tf= 16 мм, bf = 300 мм.
Окончательное значение:
A = Aw + 2·Af,
Aw = hef·tw = 106.8·0.8 = 85.14 cм²,
тогда
А = 85.14 + 2•44.35 =174.14 cм²,
Iy = tw·hef3/12 + 2·( bf · tf3/12 + bf · tf ·(h/2 - tf /2)2) (3.2.12)
Iy = 0.8·106.83/12 + 2· ( 30· 1.63/12 + 30·1.6·(110/2 – 1.6 /2)2) = 363200 cм4,
тогда
Wy = Iy / (h/2),(3.2.13)
Wx = 363200·2/110 = 6604 cм³,
Wy= 6604 cм³ > Wтр = 6351 см³
Sy = bf · tf· h0/2 + (hef · tw/2·hef/4) (3.2.14)
Sy = 30·1.6·108.4/2 + (106.8·0.8/2·106.8/4) = 3742 cм³.
Прочность сечения проверяем, исходя, из предположения упругой работы стали:
σ = Mmax·γn / Wx£Ry·γc, (3.2.15)
по СНиПу II-23-81*: Ry= 240 МПа,
σ = 1604.366·103·0.95/6604·10-6 = 230.8 МПа<240 МПа
Проверка по касательным напряжениям:
τ = Qmax·Sy·γn/Iy·tw£Rs·γc(3.2.16)
τ = 629.163·103·0.95/363200·10-8·0.008 = 76.98 МПа
τ = 76.98 МПа< 139.2 МПа
Проверка прочности стенки на совместное действие σyи τyz:
Öσy² + 3· τyz² £ 1.15·Ry·γc, (3.2.17)
σy = Mmax·γn·hef / 2·Iy, (3.2.18)
σy =1604.366·103·0.95·1.068 / 2·363200·10-8 = 224.1 МПа;
τyz = Qmax·γn/ tw·hef(3.2.19)
τyz=629.163·103·0.95/0.008·1.068 =69.96 МПа;
Ö224.1² + 3·69.96² £ 1.15·240·1,
254.763 МПа < 276 МПа.
3.2.3 Изменение сечения главной балки
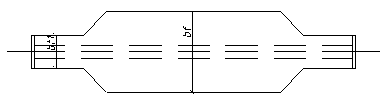
В однопролетных шарнирно опертых балках целесообразно изменять ее сечение в соответствии с эпюрой изгибающих моментов. Следуя рекомендациям, изменение сечения производим путем уменьшения bf, оставляя без изменения h, tf, tw.
Для этого ширину пояса bf1 в концевой части балки назначаем равной (0.5 – 0.75)•bf, принятой для сечения с расчетным моментом Мрасч. При этом, соблюдая условия:
bf1³ 0.1·hиbf1³160 мм(3.2.20)
bf1 = (0.5÷0.75) ·bf= 220 мм,
220 > 110 мм,
bf1 = 220 мм.
Для назначенной ширины пояса bf1 = 22 см, дополнительные условия выполняются.
После назначения bf1 находим геометрические характеристики Iy1, Wy1, Sy1.
Iy1=Iw+2· If1 = tw·hef3/12 + 2·( bf1· tf3/12 + bf1· tf ·(h/2 - tf /2)2)
Iy1= 0.8·106.83/12 + 2·( 22·1.63/12 + 22·1.6·(110/2 – 1.6 /2)2) =292700 cм4
Wy1 = 2·Iy1/h = 292700·2/110 = 5321.82 cм3;
Sy1 = hef · tw /2·hef/4 + bf1 · tf· h0/2 = 106.2·0.8/2·106.2/4 + 22·1.6·108.4/2 = 3092 cм3;
Изгибающий момент, который может быть воспринят измененным сечением, определяется по формуле:
M1 = Wx1·Ry·γc, (3.2.21)
где γс= 1.
M1 = 5321.82·10-6·240·106·1 = 1224 кНм.
Далее находим расстояние от опоры балки до ординаты М1.
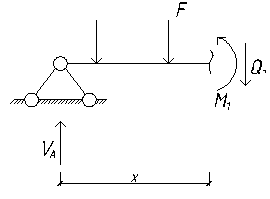
M1 - VA·x + 2·F·x – 713.052 = 0;
Решаем уравнение относительно x:
1224 – 629.163· x + 2·209.721· x – 713.052 = 0;
x = 2.436 м → x = 2.4 м.
Стык поясов в балках относим от сечения с ординатой М1 в сторону опор на 300 мм.
x– 300 = 2.4 – 0.3 = 2.1 м. Принимаем: x = 2.1 м.
Изгибающий момент в полученном сечении, будет равен:
Mрасч= VA·2,1 - F·1.25 = 629.163·2,1 – 209.721·1.25 = 1059 кНм.
В месте изменения сечения балки проводим проверки:
σ = Mрасч·γn/ Wy1£Ry·γc, (3.2.22)
σ = 1059·103·0.95 / 5231.82·10-6 = 189 МПа < 240 МПа;
τ = Qрасч·Sy1·γn/ Iy1·tw£Rs·γc, (3.2.23)
Qрасч = VA - F = 629.163 –209.721 = 419.442 кН,
τ = 419.442·103·3092·10-6·0.95 / 292700·10-8·0.008 = 52.62 МПа < 139.2 МПа.
3.2.4 Проверка общей устойчивости и деформативности балок
f/l = Mmaxn·L / 9.6·EIy£(f/L) = 1/211.667(по СНиПу II-23-81*) (3.2.24)
Mmaxn=Mmax/ k, (3.2.25)
где k = (+q) р/(+q) н, (3.2.26)
k = 18.95/15.92 = 1.19 > 1;
Mmaxn= 1604.366/1.19 = 1348.21 кНм;
f/l= 1348.21·103·10.2 / 9.6·2.06·105·106·363200·10-8 = 2.278·10-3 < 4.724·10-3
3.2.5 Проверка местной устойчивости балок
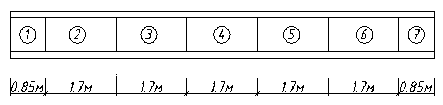
Стенки балок для обеспечения их местной устойчивости следует укреплять поперечными ребрами, поставленными на всю высоту стенки. Ребра жесткости нужны в том случае, если значение условной гибкости стенки:
λw = hef/tw·Ö Ry/E > 3.2, (3.2.27)
при отсутствии подвижной нагрузки
λw = 106.8/0.8·Ö240/2.06·105= 4.557 > 3.2.
При этом расстояние между поперечными ребрами вдоль балки принимаем, а=1,7м, которое не должно превышать, а £ 2·hef. Поперечные ребра также устанавливаться в местах приложения неподвижных сосредоточенных нагрузок, от вспомогательных балок и на опорах.
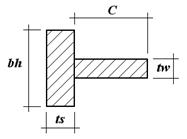
Ширина выступающей части ребра:
bh³hef/30 + 40мм, (3.2.28)
bh ³ 1068/30 + 40 = 75.6 мм,
после округления до размера кратного 10 мм, получим bh = 100 мм.
Толщина ребра:
ts³ 2·bh·Ö Ry/E, (3.2.29)
ts = 2·100·Ö240/2.06·105 = 6.827 мм,
принимаем по сортаменту ts= 7 мм.
Расчет на устойчивость стенки проверяем по формуле:
Ö(σ/σcr)² + (τ/τcr)² £ 1, (3.2.30)
σcr = Ccr·Ry/λw², (3.2.31)
Ccr = 35.5,
σcr = 35.5·240·106 / 4.557² = 410.281 МПа;
τcr = 10.3· (1 + (0.76/μ²))·Rs/λef², (3.2.32)
μ – отношение большей стороны отсека балки к меньшей, т.е.:
μ = a/hef = 1.7/1.068 = 1.59,
λef = (d/tw) ·ÖRy/E, (3.2.33)
d – меньшая из сторон отсека балки, т.е. hef = 106.8 cм;
λef = (106.8/0.8) ·Ö240/2.06·105 = 4.557,
τcr= 10.3·(1 + (0.76/1.59²))·0.58·240·106/4.557² = 89.799 МПа;
σ = (Мср·γn /Iy)·y, (3.2.34)
τ = Q·γn /(tw·hef), (3.2.35)
y = hef/2=106.8/2=53.4 см.
На устойчивость проверим 2-ой отсек:
Мср = 891.314 кНм,
Q = 419.442 кН,
σ = (891.314·103·0.95/292700·10-8)·0.534 = 154.5 МПа;
τ = 419.442·103·0.95/(0.008·1.068) = 46.64 МПа;
Ö(154.5/410.281)² + (46.64/89.799)² = 0.642 £ 1;
На устойчивость проверим 1-ой отсек:
Мср = 267.395 кНм,
Q = 629.163 кН,
σ = (267.395·103·0.95/292700·10-8)·0.534 = 46.34 МПа;
τ = 629.163·103·0.95/(0.008·1.068) = 69.96 МПа;
Ö(46.34/410.281)² + (69.96/89.799)² = 0.787 £ 1;
На устойчивость проверим 3-ой отсек:
Мср = 1426.103 кНм,
Q = 209.721кН,
σ = (1426.103·103·0.95/363200·10-8)·0.534 = 199.2 МПа;
τ = 209.721·103·0.95/(0.008·1.068) = 23.32 МПа;
Ö(199.2/410.281)² + (23.32/89.799)² = 0.551 £ 1;
На устойчивость проверим 4-ой отсек:
Мср = 1604.366 кНм,
Q = 0кН,
σ = (1604.366·103·0.95/363200·10-8)·0.534 = 224.1 МПа;
τ = 0·103·0.95/(0.008·1.068) = 0 МПа;
Ö(224.1/410.281)² + (0/89.799)² = 0.546 £ 1;
3.2.6 Расчет поясных швов, опорных частей балок, узлов сопряжений балок
Расчет поясных швов сводится к определению требуемого катета углового сварного шва kf. В балках, проектируемых, из одной марки стали, при статической нагрузке требуемый катет шва равен:
kf³ (Qрасч·Sf)/(2·Iy·βf·Rwf·γwf·γc), (3.2.36)
где Sf– статический момент полки балки;
βf = 1.1 – коэффициент, для автоматической сварки стали с Ry до 580 МПа;
γwf = 1 – коэффициент условия работы шва;
Rwf = 180 МПа – расчетное сопротивление сварного углового шва условному срезу, γс= 1.
kf ³ (419.442·103·0.95·3092·10-6)/(2·292700·10-8·1.1·180·106·1·1) = 1.06 мм,
Принимаем kf= 6 мм.
Участок стенки составной балки над опорой должен укрепляться опорным ребром жесткости и рассчитываться на продольный изгиб из плоскости как стойка высотой ls = h, нагруженная опорной реакцией Vr. В расчетное сечение включается, кроме опорных ребер и часть стенки.
Площадь опорного ребра определим из условия смятия торца по формуле:
As = bh·ts = Vr·γn /Rp, (3.2.37)
Rp = Run / γmпо СНиПу II-23-81*: Run = 370 МПа, γm = 1.025,
Rp = 370/1.025 = 368.975 МПа,
As= 629.163·103·0.95/368.975·106 = 17.05 м2
Находим ts:
ts = As /bh=17.05/22 = 0.758 см ≈ 8 мм → ts = 12 мм.
Тогда
δ £ 1.5·ts = 1.5·12 = 18 мм.
Проверка устойчивости опорной стойки относительно оси x-x производится по формуле:
σ =Vr·γn /φ·A£Ry·γc,(3.2.38)
где А – расчетная площадь стойки, равная:
A = bh·ts + 0.65·tw² ·ÖE/Ry, (3.2.39)
A = 22·1.2+ 0.65·0.8²·Ö2.06·105/240 = 39.188 см²;
φ – коэффициент продольного изгиба, определяемый по СНиПу II-23-81*, в зависимости от гибкости:
λ = lef/ix, lef = h = 110 см
ix = ÖIx/A,
где Ix– для расчетного сечения:
Ix = (ts·bh³)/12 + (0.65·tw·ÖE/Ry·tw³)/12 =
= (1.2·22³)/12 + (0.65·0.8·Ö2.06·105/240·0.8³)/12 = 1140 см4,
тогда:
ix= Ö1140/39.188 = 5.394 см, λ = 110/5.394 = 20.393,
принимаем: φ = 0,96,
σ = 629.163·103·0.95/0.96·39.188·10-4 = 158.9 МПа < 240 МПа.
Сопряжение вспомогательных балок с главными, по условиям задания рассчитываем для случая примыкания вспомогательной балки к поперечному ребру жесткости главной балки. Сопряжение производим на сварке.
Расчет сопряжения заключается в назначении требуемого катета шва kf. Длина шва lω, определяется высотой стенки вспомогательной балки lω = hef –1см, где hef =0.85·h – высота стенки прокатной балки до закругления. При проектировании ребер главных и вспомогательных балок из одной стали катет шва, равен:
kf³V·γn/(βf·lω·Ry·γωf·γc), (3.2.40)
где V – реакция вспомогательной балки;
hef = 0.85·30 = 25.5 см,
lω = 25.5 – 1 = 24.5 см,
kf³ 99.867·103·0.95/(1.1·0.245·240·106·1·1) = 1.467 мм.
Принимаем kf = 6 мм.
4. Расчет и конструирование колонн
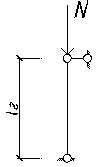
4.1 Выбор расчетной схемы
Определение расчетной сжимающей силы на колонну производим суммированием опорных реакций главных балок:
N = 2·k·V, (4.1.1)
где k = 1.03 – 1.05 – коэффициент, учитывающий собственный вес колонны;
N = 2·(1.03–1.05)·629.163 = 1309 кН.
Условия опирания колонн на фундаменты и схема связей по колоннам определяется следующими требованиями. Необходимо обеспечить геометрическую неизменяемость сооружения в плоскости и из плоскости главных балок. Из плоскости главных балок геометрическая неизменяемость, как правило, обеспечивается установкой вертикальных связей по колоннам. В плоскости главных балок путем прикрепления их к неподвижным точкам (каркасу здания).
При этом необходимо стремиться к обеспечению равно устойчивости колонн: ix/iy = lef,x/lef,y. Это достигается путем рационального выбора типа сечения и правильной ориентации его в плане сооружения.
4.2 Компоновка сечения колонны
Стержень колонны конструируем в виде прокатного швеллера.
Требуемую площадь сечения колонны, определяем по формуле:
Aтр = N·γn /2 ·φ·Ry·γc, (4.2.1)
где φ – коэффициент, на этапе компоновки определяем по предварительно заданной гибкости λз, значение которой принимаем по графику (1), рис.7. ПриN = 1309 кН, λз = 80, тогда φ = 0.686.
Атр= 1309·103·0.95/2·0.686·240·106·1 = 37.77 см².
Используя сравнительно постоянную зависимость между радиусом инерции и габаритами сечения, оцениваем ориентировочные размеры швеллера.
ix,тр = Lef,x/ λз, (4.2.2)
где Lef,x = Lef,y =lг
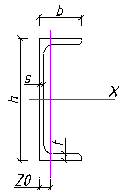
lг =H к + 0.5м = 7.8 + 0.5 = 8.3 м,
ix,тр= 830/80 = 10.375 см;
По сортаменту ГОСТ 8240-89 принимаем два швеллера № 30
А0 = 40.5 см2 ; Ix0= 5810 см4;
Iy0= 327 см4; = 100 мм;
t= 11 мм; ix0 = 12 см
h = 300 мм; iy0 = 2.84 см;
z0 = 2.52 см; = 6.5 мм;
Задаваясь гибкостью отдельной ветви относительно собственной оси λз= 35 и шириной планки d = 250 мм, находим количество планок на колонне:
m ³lг/(λ1·i1 + d) – 1, (4.2.3)
где i1= iy0,
λ1= λз,
m ³ 830 /(35·2,84 + 25) – 1 = 5,672
m =6,
lв= lг/(m+1) – d, (4.2.4)
lв= 830/(6+1) – 25 = 96.571 см ≈ 94 см,
λ1 = lв/ i1,(4.2.5)
λ1= 94/ 2.84 = 33.099,
λx= Lef,x/ix0,(4.2.6)
λx= 830/12 = 69.167.
Для нахождения ширины сечения используют условие равноустойчивости:
λx= Lef,x=Öλy2 + λ12
λy=Öλx2–λ12,(4.2.7)
λy =Ö69.1672 – 33.0992 = 60.733,
iy,тр=Lef,y/ λy,(4.2.8)
iy,тр= 830/ 60.733 = 13.66,
Используя известную зависимость между радиусом инерции и габаритом сечений, находят значение:
тр = iy,тр / 0.44,(4.2.9)
тр= 13.66 / 0.44 = 31.059 см,
= 31 см.
Принятый размер должен обеспечивать необходимый зазор между кромками полок ветвей:
³ 2·f + 100 мм,
³ 2·100 + 100 = 300 мм,
Конструирование планок:
Для обеспечения работы колоны, как безраскосной фермы планки должны обладать достаточной изгибной жесткостью относительно свободной оси х-х. Высота планки:
ds = (0.5÷0.8)· (4.2.10)
ds= (0.5÷0.8)·310 = 190 мм.
Длина планки ls назначается такой, чтобы нахлест на каждую ветвь был не менее 5t, где t- наименьшая толщина соединяемых элементов. Толщину планок назначают в пределах 6…12 мм. таким образом, чтобы обеспечить ее местную устойчивость:
ts = (1/10…1/25)·ds (4.2.11)
Принимаем: ts= 8 мм; ds= 180 мм; ls= 250 мм.
4.3 Проверка сечения сквозной колонны
Для принятого сечения определяем фактические геометрические характеристики А, Ix, Iy, ix, iy и проводим проверки.
А =2·А0 =2·40.5 = 81 см²; (4.3.1)
Ix = 2·Ix0 =2·5810 = 11620 см4; (4.3.2)
Iy = 2• (Iy0 + A0·(b1/2)2) = 2· (327+40.5· (25.96/2)2) = 14300 см4; (4.3.1)
ix = iх0 = 12 см; (4.3.3)
iy = ÖIy/A = Ö14300/81 = 13.287 см. (4.3.1)
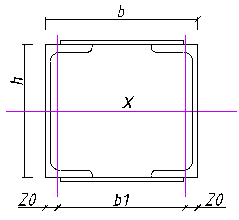
λy= Lef,у/ iу(4.3.4)
λy = 830/13.287 = 62.467
λх= Lef,х/ ix (4.3.5)
λх = 830/12 = 69.167;
Проводим проверки прочности гибкости и общей устойчивости стержня колоны.
Проверка общей устойчивости выполняется по формуле:
N·γn/φmin·A £ Ry·γс, (4.3.6)
где φmin – определяется по максимальной величине λx, λy;
принимаем φmin= 0.758, тогда:
1309·103·0.95/0.758·81 = 202.5 МПа < 240 МПа.
Проверка выполняется, тогда автоматически выполняется проверка прочности.
Проверку гибкости колонн, производим по формулам:
λx = Lef,x/ix£ |λ|, λy = Lef,y/iy£ |λ|, (4.3.7)
где |λ| - предельная гибкость колонн, определяем по СНиПу II-23-81*:
λ| = 180 – 60·α, (4.3.8)
α = N·γn /Ry·γc·A·φmin = 1309·103·0.95/240·106·1·81·10-4·0.758 = 0.844; (4.3.9)
λ = 180 – 60·0,893 = 129.36
тогда:
λ = 830/12 = 69.17 < 129.36; λ = 830/13.287 = 62.47 < 129.36,
гибкость колонн обеспечена.
Расчет планок центрально-жатых колон и их соединений ведут на усилия, возникающие от условной поперечной силы, которую принимают постоянной по всей длине колонны:
Qfic = 7.15∙10-6·(2330 – E/Ry)·N·γn /φ ; (4.3.10)
Qfic = 7.15·10-6· (2330-2.06∙105/240)·1309·103·0.95/0.758=17.26 кН,
где φ – коэффициент продольного изгиба, принимается в плоскости соединительных элементов по λef. Условная поперечная сила распределяется поровну между планками двух граней:
Qs = Qfic/2 (4.3.11)
Qs= 17.26/2 = 8.63 кН,
В каждой планке, как в стойке безраскосной фермы возникает поперечная сила:
Fs=Qs·l/b (4.3.12)
Fs= 8.63·103·0.25/0.31 =6.96 кН,
и изгибающий момент в месте прикрепления к ветвям:
Ms=Qs·l/2 (4.3.13)
Ms=8.63·103·0.25/2 = 1.09 кНм,
Проверка прочности планок:
σ =Ms·γn /Ws≤ Ry·γc(4.3.14)
Ws=ts·ds2/6 (4.3.15)
Ws= 0.8·192/6 =48.133 см3
σ = 1.09·103·0.95/48.133·10-6 = 39.18 МПа < 240 МПа.
Сварные угловые швы, прикрепляющие планки к ветвям колоны, рассчитываются на совместное действие усилий в планке Ms и Fs по формулам (проверка прочности по металлу):
Öσω2 + τω2 ≤ Rωf·γωf·γc(4.3.16)
σω= Ms·γn /Wω(4.3.17)
σω=1.09·103·0.95/30.24·10-6 = 34.24 МПа
τω=Fs·γn /Aω(4.3.18)
τω=6.96·103·0.95/10.08·10-4 = 6.56 МПа
Wω=βf·kf·lω2/6 (4.3.19)
Wω=0.7∙0.8·182/6 = 30.24 см3
Aω= βf·kf·lω(4.3.20)
Aω= 0.7·0.8·18 = 10.08 см2
Ö34.242 + 6.562 = 34.863 ≤ 180 МПа
где βf - коэффициент проплавления углового