Изучение гидравлики как теоретической дисциплины

Гидравлика представляет собой теоретическую дисциплину, изучающую вопросы, связанные с механическим движением жидкости в различных природных и техногенных условиях. Поскольку жидкость (и газ) рассматриваются как непрерывные и неделимые физические тела, то гидравлику часто рассматривают как один из разделов механики так называемых сплошных сред, к каковым принято относить и особое физическое тело - жидкость. По этой причине гидравлику часто называют механикой жидкости или гидромеханикой; предметом её исследований являются основные законы равновесия и движения жидкостей и газов. Как в классической механике в гидравлике можно выделить общепринятые составные части: гидростатику, изучающую законы равновесия жидкости; кинематику, описывающую основные элементы движущейся жидкости и гидродинамику, изучающую основные законы движения жидкости и раскрывающую причины её движения. Гидравлику можно назвать базовой теоретической дисциплиной для обширного круга прикладных наук, с помощью которых исследуются процессы, сопровождающие работу гидравлических машин, гидроприводов. С помощью основных уравнений гидравлики и разработанных ею методов исследования, решаются важные практические задачи, связанные с транспортом жидкостей и газов по трубопроводам, а также с транспортом твёрдых тел по трубам и другим руслам. Гидравлика также решает важнейшие практические задачи, связанные с равновесием твёрдых тел в жидкостях и газах, т.е. изучает вопросы плавания тел.

Широкое применение гидравлики

Широкое использование в практической деятельности человека различных гидравлических машин и механизмов ставят гидравлику в число важнейших дисциплин, обеспечивающих научно-технический прогресс. Большой практический интерес к изучению механики жидкости вызван рядом объективных факторов. В - первых, наличие в природе значительных запасов жидкостей, которые легко доступны человеку. Во- вторых, жидкие тела обладают рядом полезных свойств, делающих их удобными рабочими агентами в практической деятельности человека. Немаловажным следует считать и тот фактор, что большинство жизненно важных химических реакций обмена протекают в жидкой фазе (чаще всего в водных растворах). По этим причинам особый интерес человек проявил к жидкостям на самой ранней стадии своего развития. Вода и воздух (иначе жидкость и газ) были отнесены к числу основных стихий природы уже первобытным человеком. История свидетельствует об успешном решении ряда практических задач с использованием жидкостей уже на самих ранних стадиях развития человека. Первым же научным трудом по гидравлике следует считать трактат Архимеда «О плавающих телах» (250 г. до н. э.)- Однако в дальнейшем на протяжении нескольких столетий в развитии человечества наступила эпоха всеобщего застоя, когда развитие знаний и практического опыта находились на весьма низком уровне. В последующую за этим эпоху возрождения началось бурное развитие человеческих знаний, науки, накопление практического опыта. Наравне с развитием других наук начала развиваться и наука об изучении взаимодействия жидких тел. Первыми крупными работами в этой области следует считать работы Леонардо да Винчи (1548-1620) - в области плавания тел, движения жидкостей по трубам и каналам. В работах Галилео Галилея (1564-1642) были сформулированы основные принципы равновесия и движения жидкости; работы Эванджелиста Торричелли (1604 - 1647) были посвящены решению задач по истечению жидкости из отверстий, а Блез Паскаль (1623 - 1727) исследовал вопросы по передаче давления в жидкости. Основополагающие и обобщающие работы в области механики физических тел, в том числе и жидких, принадлежат гениальному английскому физику Исааку Ньютону (1643 - 1727), который впервые сформулировал основные законы механики, закон всемирного тяготения и закон о внутреннем трении в жидкостях при их движении.

Развитию гидромеханики (гидравлики) как самостоятельной науки в значительной степени способствовали труды русских учёных Даниила Бернулли (1700 - 1782), Леонарда Эйлера (1707 - 1783), М.В. Ломоносова (1711 - 1765). Работы этих великих русских учёных обеспечили настоящий прорыв в области изучения жидких тел: ими впервые были опубликованы дифференциальные уравнения равновесия и движения жидкости Эйлера, закон сохранения энергии Ломоносова, уравнение запаса удельной энергии в идеальной жидкости Бернулли. Развитию гидравлики как прикладной науки и сближению методов изучения теоретических и практических вопросов используемых гидравликой и гидромеханикой способствовали работы французских учёных Дарси, Буссинэ и др., а также работы Н.Е. Жуковского. Благодаря трудам этих учёных, а также более поздним работам Шези, Вейсбаха, Прандля удалось объединить теоретические исследования гидромеханики с практическими и экспериментальными работами, выполненными в гидравлике. Работы Базена, Пуазейля, Рейнольдса, Фруда, Стокса и др. развили учение о динамике реальной (вязкой жидкости). Дифференциальное уравнение Навье - Стокса позволило описать движение реальной жидкости как функцию параметров этой жидкости в зависимости от внешних условий.

Методы исследования

Дальнейшие работы в области теоретической и прикладной гидромеханики были направлены на развитие методов решения практических задач, развитие новых методов исследования, новых направлений: теория фильтрации, газо- и аэродинамика и др. При решении практических вопросов гидравлика оперирует всеми известными методами исследований: методом анализа бесконечно малых величин, методом средних величин, методом анализа размерностей, методом аналогий, экспериментальным методом.

· Метод анализа бесконечно малых величин - наиболее удобный из всех методов для количественного описания процессов равновесия и движения жидкостей и газов. Этот метод наиболее эффективен в тех случаях, когда приходится рассматривать движение объектов на атомно-молекулярном уровне, т.е. в тех случаях, когда для вывода уравнений движения приходится рассматривать жидкость (или газ) с молекулярно-кинетической теории строения вещества. Основной недостаток метода - довольно высокий уровень абстракции, что требует от читателя обширных знаний в области теоретической физики и умение пользоваться различными методами математического анализа, включая векторный анализ.

· Метод средних величин - является более доступным методом, поскольку его основные положения базируется на простых (близких к обыденным) представлениях о строении вещества. При этом выводы основных уравнений в большинстве случаев не требуют знаний молекулярно-кинетической теории, а результаты, полученные при исследованиях, этим методом не противоречат «здравому смыслу» и кажутся обоснованными. Недостаток этого метода исследований связан с необходимостью иметь некоторые априорные представления о предмете исследований. Метод анализа размерностей может рассматриваться в качестве одного из дополнительных методов исследований и предполагает всестороннее знания изучаемых физических процессов.

· Метод аналогий - используется в тех случаях, кода имеются в наличии детально изученные процессы, относящиеся к тому же типу взаимодействия вещества, что и изучаемый процесс.

· Экспериментальный метод является основным методом изучения, если другие методы по каким- либо причинам не могут быть применены. Этот метод также часто используется как критерий для подтверждения правильности результатов полученных другими методами.

В конечном счёте, метод изучения движения жидкости, а также уровень изучения (макро или микро) выбирается из условий практической постановки задач и соотношения характерных размеров. Основным мерилом для этих характерных размеров может быть длина свободного пробега молекул. Так для изучения движения жидкости на макро уровне необходимо, чтобы характерные размеры: L (некоторая длина) и d (ширина) по отношению к длине свободного пробега молекул А, находились в соответствии:

Жидкость как физическое тело

Чтобы представить и правильно понять характер поведения жидкости в различных условиях необходимо обратиться к некоторым представлениям классической физики о жидкости как физическом теле. Не ставя перед собой цель детального и всестороннего описания жидких тел, что подробно рассматривается в классическом курсе физики, напомним лишь некоторые положения, которые могут пригодиться при изучении гидравлики как самостоятельной дисциплины. Так, согласно молекулярно-кинетической теории строения вещества все физические тела в природе (независимо от их размеров) находятся в постоянном взаимодействии между собой. Степень (интенсивность) взаимодействия зависит от масс этих тел и от расстояния между телами. Количественной мерой взаимодействия тел является сила, которая пропорциональна массе тел и всегда будет убывать при увеличении расстояния между телами. В зависимости от размеров тел (элементарные частицы, атомы и молекулы, макротела) характер взаимодействия будет различным. Согласно классическим представлениям физики можно выделить четыре вида взаимодействия тел. Каждый вид взаимодействия обусловлен наличием своего переносчика взаимодействия. Два вида взаимодействия относятся к типу дальнодействующих и повседневно наблюдаются человеком: гравитационное и электромагнитное. При электромагнитном взаимодействии происходит процесс излучения и поглощения фотонов. Именно этот процесс порождает электромагнитные силы, под действием которых протекают практически все процессы в природе, которые мы наблюдаем. Характерной особенностью этого (электромагнитного) взаимодействия является то, что его проявление зависит от многих внешних условий, которые приводят к различным наблюдаемым результатам. Так имея одну и ту же природу взаимодействия (электромагнитную) мы изучаем, на первый взгляд, совершенно разные физические процессы: движение жидкости, трение, упругость, передачу тепла, движение зарядов в электрическом поле и т.д. И, как следствие, дифференциальные уравнения, описывающие эти процессы, одинаковые. Согласно молекулярно-кинетической теории строения вещества молекулы находятся в равновесии и, как материальные объекты постоянно взаимодействуют друг с другом. Такое равновесие нельзя считать абсолютным, т.к. молекулы находятся в состоянии хаотического движения (колебания) вокруг центра своего равновесия. Расстояния между молекулами вещества будет зависеть от величин сил действующих на молекулы. Независимо от природы действующих сил их можно сгруппировать на силы притяжения и силы отталкивания. Условие равновесия этих сил определяет оптимальные расстояния между молекулами. Однако, в связи с тем, что такое равновесие между действующими силами является динамическим равновесием, молекулы находятся в постоянном колебательном движении относительно друг друга, испытывая при этом действие некоторой равнодействующей силы порождаемой силами притяжения и отталкивания. Поэтому особенности состояния вещества будут зависеть от соотношения между кинетической энергией колебательного движения молекул вещества и энергией взаимодействия между молекулами вещества. Так при больших массах молекул энергия взаимодействия между молекулами многократно превышает кинетическую энергию колебательного движения вещества, вследствие чего молекулы вещества занимают устойчивое положение относительно друг друга, обеспечивая тем самым постоянство формы и размеров макротела. Такие вещества, как известно, относятся к категории твёрдых тел. Противоположными особенностями характеризуются вещества, состоящие из «лёгких» молекул (молекул обладающих малой массой). Такие вещества обладают кинетической энергией колебательного движения молекул вещества превышающей многократно энергию взаимодействия между молекулами, из которых вещество состоит. По этой причине молекулы такого вещества имеют очень слабую связь между собой и легко перемещаются в пространстве на любые расстояния. Такое свойство вещества носит название диффузии (летучести). Вещества, обладающие эти свойством, относятся к категории газов. В тех случаях, когда энергия взаимодействия имеет тот же порядок, что и величина кинетической энергии колебательного движения молекул, последние обладают свойством относительной подвижности, но, при этом, сохраняют целостность самого макротела. Такое тело обладает способностью легко деформироваться при минимальных касательных напряжениях, т. е. такое тело обладает текучестью. На самом деле колебательный процесс среди молекул жидких тел достаточно сложен, и с целью простого описания данного процесса можно нарисовать упрощенную картину взаимодействия молекул жидкости. Так в отличие от молекул в твёрдых телах, при колебательном процессе в жидкости центры взаимодействия молекул могут смещаться в пространстве настолько, на сколько это допускают расстояния между молекулами (до величины 1x10 " см). Смещение центра равновесия сил в пространстве называется релаксацией. Время, за которое происходит такое смещение, называется временем релаксации, t₀. При этом смещение центра равновесия осуществляется не постепенно, а скачком. Таким образом, время релаксации характеризует продолжительность «оседлой жизни» молекул жидкости. Если на жидкость будет действовать некоторая сила F, то при совпадении линии действия этой силы с направлением скачка, жидкость начнёт перемещаться. При этом необходимо выполнение дополнительного условия: продолжительность действия силы должна быть больше длительности времени релаксации t₀, т.к. в противном случае жидкость не успеет начать своё движение, и будет испытывать упругое сжатие подобно твёрдому телу. Тогда процесс движения жидкости будет характеризовать свойство текучести присущее практически только жидким телам. Тела с такими свойствами относятся к категории жидких тел. При этом следует отметить, что чётких и жёстких границ между твёрдыми, жидкими и газообразными телами нет. Имеется большая группа тел занимающих промежуточное положение между твёрдыми телами и жидкостями и между жидкостями и газами. Вообще говорить о состоянии вещества можно только при вполне определённых внешних условиях. В качестве стандартных условий приняты условия при температуре 20 °С и атмосферном давлении. Стандартные (нормальные) условия вполне соотносятся с понятием благоприятных внешних условий для существования человека. Понятие о состоянии вещества необходимо дополнить. Так при увеличении кинетической энергии молекул вещества (нагрев вещества) твёрдые тела могут перейти в жидкое состояние (плавление твёрдого тела) и твёрдые тела приобретут при этом некоторые свойства жидкостей. Подобно этому увеличение кинетической энергии молекул жидкого вещества может привести жидкость в газообразное состояние (парообразование) и при этом жидкость будет иметь свойства соответствующие газам. Аналогичным способом можно превратить расплавленное твёрдое тело в пар, если в большей степени увеличить кинетическую энергию колебательного движения молекул первоначального твёрдого вещества. Уменьшение кинетической энергии молекул (охлаждение вещества) приведёт процесс в обратном направлении. Газ может быть превращён в жидкое, а, затем и в твёрдое состояние.

Изучение реальных жидкостей и газов

Изучение реальных жидкостей и газов связано со значительными трудностями, т.к. физические свойства реальных жидкостей зависят от их состава, от различных компонентов, которые могут образовывать с жидкостью различные смеси как гомогенные (растворы) так и гетерогенные (эмульсии, суспензии и др.) По этой причине для вывода основных уравнений движения жидкости приходится пользоваться некоторыми абстрактными моделями жидкостей и газов, которые наделяются свойствами неприсущими природным жидкостям и газам. Идеальная жидкость - модель природной жидкости, характеризующаяся изотропностью всех физических свойств и, кроме того, характеризуется абсолютной несжимаемостью, абсолютной текучестью (отсутствие сил внутреннего трения), отсутствием процессов теплопроводности и теплопереноса.

Реальная жидкость - модель природной жидкости, характеризующаяся изотропностью всех физических свойств, но в отличие от идеальной модели, обладает внутренним трением при движении. Идеальный газ - модель, характеризующаяся изотропностью всех физических свойств и абсолютной сжимаемостью. Реальный газ - модель, при которой на сжимаемость газа при условиях, близких к нормальным условиям существенно влияют силы взаимодействия между молекулами. При изучении движения жидкостей и газов теоретическая гидравлика (гидромеханика) широко пользуется представлением о жидкости как о сплошной среде. Такое допущение вполне оправдано, если учесть, что размеры пространства занимаемого жидкостью, во много раз превосходят межмолекулярные расстояния (исключением можно считать лишь разряженный газ). При изучении движения жидкостей и газов последние часто рассматриваются как жидкости с присущими им некоторыми особыми свойствами. Всвязи с этим принято различать две категории жидкостей: капельные жидкости (практически несжимаемые тела, или собственно жидкости) и сжимаемые жидкости (газы).

Основные физические свойства жидкостей

К основным физическим свойствам жидкостей следует отнести те её свойства, которые определяют особенности поведения жидкости при её движении. Такими являются свойства, характеризующие концентрацию жидкости в пространстве, свойства, определяющие процессы деформации жидкости, определяющие величину внутреннего трения в жидкости при её движении, поверхностные эффекты. Важнейшим физическим свойством жидкости, определяющим её концентрацию в пространстве, является плотность жидкости. Под плотностью жидкости понимается масса единицы объёма жидкости:

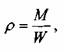
где: М - масса жидкости,

W - объём, занимаемый жидкостью.

В международной системе единиц СИ масса вещества измеряется в кг, объём жидкого тела в м ³ , тогда размерность плотности жидкости в системе единиц СИ - кг/м ³. В системе единиц СГС плотность жидкости измеряется в г/см ³. Величины плотности реальных капельных жидкостей в стандартных условиях изменяются в системе единиц СИ в широких пределах от 700 кг/м ³ до 1800 кг/м ³, а плотность ртути достигает 13550 кг/м , плотность чистой воды составляет 998 кг/м ³. В системе единиц СГС пределы изменения плотности жидкости от 0,7 г/см до 1,8 г/см ³, плотность чистой воды 0,998 г/см . Величины плотности газов меньше плотности капельных жидкостей приблизительно на три порядка, т.е. в системе единиц СИ плотности газов при атмосферном давлении и температуре О °С изменяются в пределах от 0,09 кг/м ³ до 3,74 кг/м, плотность воздуха составляет 1,293 кг/м ³.

Плотность капельных жидкостей и газов зависит от температуры и давления. Зависимость величины плотности жидкости и газа при температуре отличной от 20 °С определяется по формуле Д.И. Менделеева:

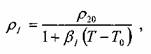
где: р и р₂₀ - плотности жидкости (газа) при температурах соответственно

ГиГ_о=20°С, βi- коэффициент температурного расширения. Исключительными особенностями обладает вода, максимальная плотность которой отмечается при 4 °С. Плотность капельных жидкостей в зависимости от давления может быть определена в соответствии с уравнением состояния упругой жидкости:

• где: - плотность капельной жидкости при атмосферном давлении р_ат , - коэффициент объёмного сжатия капельной жидкости.

Плотность идеальных газов при давлениях отличных от атмосферного можно определить по известному закону газового состояния Менделеева-Клайперона:

Где задействовано давление, удельный объём газа, универсальная газовая постоянная, температура газа.

при

Кроме абсолютной величины плотности капельной жидкости, на практике пользуются и величиной её относительной плотности, которая представляет собой отношение величины абсолютной плотности жидкости к плотности чистой воды при температуре 4 °С:

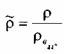Относительная плотность жидкости - величина безразмерная.

Имеется аналогичная характеристика и для газов. Под относительной плотностью газа (по воздуху) понимается отношение величины абсолютной плотности газа к плотности воздуха при стандартных условиях.

Плотность жидкости

О плотности жидкости косвенно можно судить по весовому показателю, - удельному весу жидкости. Под удельным весом жидкости (газа) понимается вес единицы объёма жидкости (газа):

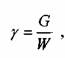
G вес жидкости (газа),

где: W объем, занимаемый жидкостью (газом).

Связь между плотностью и удельным весом жидкости такая же как и между массой тела и её весом:

Размерность удельного веса жидкости в системе единиц СИ н/м ³ , удельный вес чистой воды составляет 9810 н/м³. Аналогично вводится понятие об относительном удельном весе жидкости,

На практике величина плотности жидкости определяется с помощью простейшего прибора - ареометра. По глубине погружения прибора в жидкость судят о её плотности.

Упругость

Об упругости можно сказать тоже, так как капельные жидкости относятся к категории плохо сжимаемых тел. Причины незначительных изменений объёма жидкости при увеличении давления очевидны, т.к. межмолекулярные расстояния в капельной жидкости малы и при деформации жидкости приходится преодолевать значительные силы отталкивания, действующие между молекулами, и даже испытывать влияние сил, действующих внутри атома. Тем не менее, сжимаемость жидкостей в 5 - 10 раз выше, чем сжимаемость твёрдых тел, т.е. можно считать, что все капельные жидкости обладают упругими свойствами. Оценка упругих свойств жидкостей может осуществляться по ряду специальных параметров, коэффициент объёмного сжатия жидкости представляет собой относительное изменение объёма жидкости при изменении давления на единицу. По существу это известный закон Гука для модели объёмного сжатия:

Формула включает начальный объём жидкости, (при начальном давлении), и коэффициент объёмного (упругого) сжатия жидкости. Считается, что коэффициент объёмного сжатия жидкости зависит с достаточно большой точностью только от свойств самой жидкости и не зависит от внешних условий. Коэффициент объёмного сжатия жидкости имеет размерность обратную размерности давления, т.е. м/н. адиабатический модуль упругости жидкости К, зависящий от термодинамического состояния жидкости (величина обратная коэффициенту объёмного сжатия жидкости):

Величина модуля упругости жидкости имеет размерность напряжения, т.е. н/м. Об упругих свойствах капельной жидкости можно судить по скорости распространения продольных волн в жидкой среде, которая равна скорости звука в покоящейся жидкости:

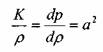
С упругими свойствами капельных жидкостей также связаны представления о сопротивлении жидкостей растяжению. Теоретически в чистых жидкостях могут быть достигнуты довольно значительные напряжения. Однако, в реальных жидкостях при наличии в них даже весьма незначительных примесей (твёрдые частицы, газ) уменьшает величину сопротивления жидкости растяжению практически до 0. По этой причине можно считать, что в капельных жидкостях напряжения растяжению невозможны. Об упругих свойствах газов можно судить исходя из классического уравнения Пуассона:

;

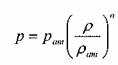где: п - показатель адиабаты равный отношению теплоёмкости газа при постоянном давлении к величине теплоёмкости газа при постоянном объёме.

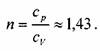
Для оценки упругих свойств движущегося газа пользуются не абсолютной величиной скорости звука с_зв, а отношением скорости потока газа v к скорости звука в газе. Этот показатель носит название числа Маха:

Вязкость

И немного о вязкости. При движении реальных (вязких) жидкостей в них возникают внутренние напряжения, обусловленные силами внутреннего трения жидкости. Природа этих сил довольно сложна; возникающие в жидкости напряжения связаны с процессом переноса импульса(вектора массовой скорости движения жидкости). При этом возникающие в жидкости напряжения обусловлены двумя факторами: напряжениями, возникающими при деформации сдвига и напряжениями, возникающими при деформации объёмного сжатия. Наличие сил вязкостного трения в движущейся жидкости подтверждается простым и наглядным опытом. Если в цилиндрическую ёмкость, заполненную жидкостью опустить вращающийся цилиндр, то вскоре придёт в движение (начнёт вращаться вокруг своей оси в том же направлении, что и вращающийся цилиндр) и сама ёмкость с жидкостью. Этот факт свидетельствует о том, что вращательный момент от вращающегося цилиндра был передан через вязкую жидкость самой ёмкости, заполненной жидкостью. Напряжения, возникающие при деформации сдвига согласно гипотезе Ньютона пропорциональны градиенту скорости в движущихся слоях жидкости, а сила трения между слоями движущейся жидкости будет пропорциональна площади поверхности движущихся слоев жидкости:

где:

T - сила трения между слоями движущейся жидкости,

S- площадь поверхности слоев движущейся жидкости,

t - касательные напряжения, возникающие в жидкости при деформации сдвига,

коэффициент динамической вязкости жидкости.

Величина коэффициента динамической вязкости жидкости при постоянной температуре и постоянном давлении зависит от внутренних (химических) свойств самой жидкости. Размерность коэффициента динамической вязкости в системе единиц СИ: н с/м ², в системе СГС - д-с/см . Последняя размерность носит название пуаза (пз). Таким образом, \пз =1 д-с/см ,

а соотношение между единицами вязкости. 1да=0,1 н с/м ². Помимо коэффициента динамической вязкости жидкости широко используется коэффициент кинематической вязкости жидкости v, представляющий собой отношение коэффициента динамической вязкости к плотности жидкости:

В системе единиц СИ коэффициент кинематической вязкости измеряется в м/с, в системе единиц СГС единицей измерения коэффициента кинематической вязкости жидкости является стоке (cm), т.е. 1 cm = 1 см /с.

Коэффициент динамической вязкости чистой воды составляет 1-10~³ н-с/м (или 0,01 пз), коэффициент кинематической вязкости чистой воды составляет МО" м /с (или 0,01 cm). Коэффициенты вязкости жидкостей варьируют в весьма широких пределах от 0,0003 до 0,139 н-с/л/².

Вязкость жидкости в значительной степени зависит от температуры и давления. При увеличении температуры капельной жидкости коэффициенты её вязкости (как динамический, так и кинематический) резко снижается в десятки и сотни раз, что обусловлено увеличением внутренней энергии молекул жидкости по сравнению с энергией межмолекулярной связи в жидкости. Зависимость вязкости капельной жидкости от температуры может быть выражена в виде экспоненциальной зависимости:

где:

_Q - 20 °С,

- экспериментальный температурный коэффициент. Зависимость вязкости жидкости от авления в широком диапазоне давлений остаётся практически линейной:

где: - вязкость жидкости при атмосферном давлении, а_р – экспериментальный коэффициент пропорциональности. Газы обладают несравнимо более низкими коэффициентами вязкости от 0,0000084 до 0,0000192 н-с/м ², и в отличие от капельных жидкостей вязкость газов увеличивается при увеличении температуры, т.к. с увеличением температуры газа возрастают скорости теплового движения молекул и, соответственно, увеличивается число соударений молекул газа, что делает газ более вязким. Зависимость вязкости газа от давления ничем не отличается от аналогичной зависимости для капельных жидкостей. Измерение вязкости жидкостей осуществляется с помощью вискозиметров, работающих на принципе истечения жидкости через малое калиброванное отверстие; вязкость вычисляется по скорости истечения.

Кроме деформации сдвига внутреннее сопротивление в жидкости возникает и при объёмном сжатии жидкости, т.е. сжимаемая жидкость стремится восстановить состояние первоначального равновесия. Этот процесс, в некоторой степени, аналогичен проявлению сил сопротивления при деформации сдвига, хотя сам процесс и отличается по своей сути. По этой причине говорят, что в жидкости проявляется так называемая вторая вязкость £, обусловленная деформацией объёмного сжатия жидкости.

Список используемой литературы

1. «Гидравлика» Агроскин И.И, Дмитриев Г.Т., Пикалов Ф.И., 2000г.

2. «Гидравлика» Рабинович Е.З.,2000г.

3. «Механика жидкости, гидравлические машины и основы

Гидропривода» Орлов Ю.М., 2001г.

4. «Гидравлика и гидромашины» Соколов Б.А., 2007г.