Зонная теория твердых тел

Зонная теория твердых тел

1. Металлы, хорошо проводят электрический ток.

Диэлектрики (изоляторы) плохо проводят ток.

Электропроводность металлов 10⁶ – 10⁴ (Ом×см)^-1

Электропроводность диэлектриков менее 10^-10 (Ом×см)^-1

Твердые тела с промежуточной электропроводностью называются полупроводниками.

2. Различие полупроводников и металлов проявляется в характере зависимости электропроводности от температуры.

Рис.1

С понижением температуры проводимость металлов возрастает, и для чистых металлов стремится к бесконечности при приближении к абсолютному нулю. У полупроводников, напротив, с понижением температуры проводимость убывает, а вблизи абсолютного нуля полупроводник становится изолятором.

3. Ни классическая электронная теория электропроводности, ни квантовая теория, основанная на модели свободных фермианов, не может дать ответа на вопрос, почему одни тела являются полупроводниками, а другие проводниками или диэлектриками.

4. Для ответа на вопрос необходимо методами квантовой механики рассмотреть вопрос взаимодействия валентных электронов с атомами кристаллической решетки.

5. Решить уравнение Шредингера с числом переменных порядка 10²³ – это математическая задача безнадежной трудности.

Поэтому современная квантовая теория твердого тела основывается на ряде упрощений. Такой теорией является теория твердого тела. Название связано с характерной группировкой энергетических уровней электронов в кристаллах в зоны уровней.

В основе зонной теории лежат следующие предположения:

1) При изучении движения валентных электронов положительные ионы кристаллической решетки, ввиду их большой массы, рассматриваются как неподвижные источники поля, действующего на электроны.

2) Расположение положительных ионов в пространстве считается строго периодическим: они размещаются в узлах идеальной кристаллической решетки данного кристалла.

3) Взаимодействие электронов друг с другом заменяется некоторым эффективным силовым полем.

Задача сводится к рассмотрению движения электрона в периодическом силовом поле кристалла.

Потенциальная энергия электрона U(r) периодически изменяется.

§2. Простейшая модель кристаллического тела

Это модель одномерная Кронига - Пенни, периодическое электрическое поле положительных ионов кристалла апроксимируется потенциалом типа «зубчатой стенки».

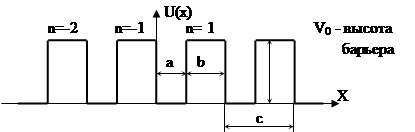Рис.2

На рисунке изображено чередование потенциальных ям и барьеров.

Решение уравнения Шредингера для потенциальной ямы:

(1)

Решение для потенциального барьера:

(2)

где ;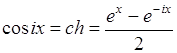

, .

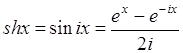
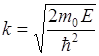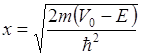X_n – координата отсчитывается от начала n^го участка. Записывают для каждой ямы и барьера, потом «сшивают» решения и получают основное уравнение для определения энергетических уровней в периодическом поле кристалла.

(3)

где 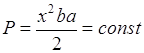-площадь зубца.

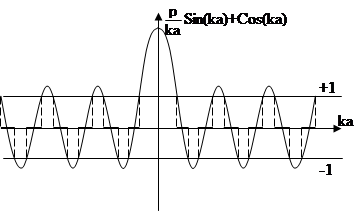Рис.3

Графическое изображение решения уравнения Шредингера по Кронигу – Пенни.

Cos k′a может меняться в пределах от –1 до +1.

Провели параллельные прямые оси абсцисс и находим точки пересечения этих прямых с графиком, опускаем перпендикуляры и находим корни уравнения (3). Эти участки обозначены жирными линиями. Таким образом допустимые значения Е(к) имеют дискретный характер (зонный). Если ось (Ка) перевернуть в вертикальное положение, то получим картину расположения энергетических зон, разрешенных и запрещенных.

Рис.4

На рис.4 энергетический спектр электронов в кристалле имеет зонную структуру.

L – длина кольца цепочки.

Значения волновых векторов . α - постоянная решетки.

Зону, произошедшую от валентных уровней атомов, образующих кристалл, называют валентной зоной.

Зоны, произошедшие от внутренних уровней, всегда полностью заполнены электронами.

Частично заполненной или незаполненной может быть внешний валентный уровень (зона проводимости).

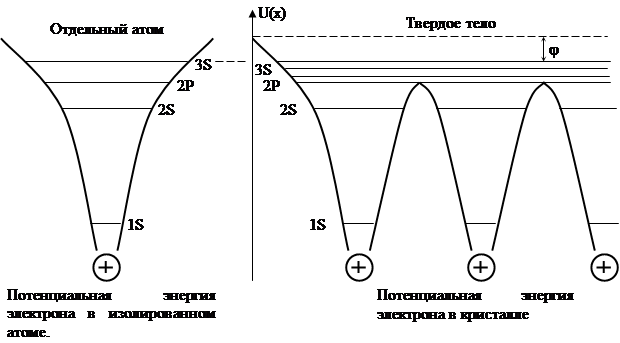
Рис.5 Рис.6

Наиболее слабо связаны 3S-электроны. При образовании твердого тела из отдельных атомов происходит перекрытие волновых функций этих электронов.

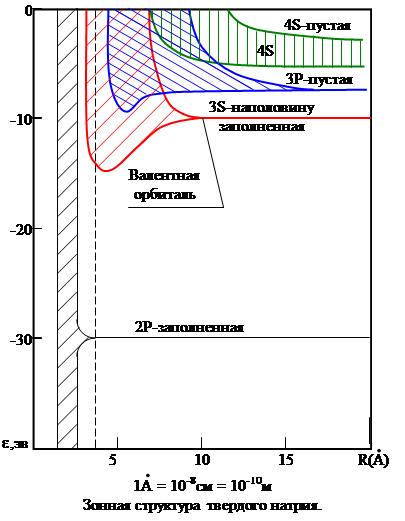Пространственная протяженность электронных волновых функций зависит от квантовых чисел. Для больших квантовых чисел электронные волновые функции простираются на большие расстояния от ядра, для этих уровней взаимное влияние атомов будет проявляться при больших расстояниях между атомами. Что хорошо видно на рис.7, на примере уровней атомов натрия. На уровнях 1S, 2S, 2P практически не сказывается влияние соседних атомов, тогда как для уровней 3S, 3P и более высоких уровней это влияние существенно и эти уровни превращаются в энергетические зоны. Для 3S – электронов имеется энергетический минимум, обеспечивающий устойчивую твердотельную конфигурацию атомов натрия при средней межатомной расстоянии R~ 3А. В атоме натрия на энергии 3S – электрона сказывается влияние соседних атомов, означает также заметное перекрытие волновых функций этих электронов. Поэтому уже нельзя говорить о том, что конкретный 3S – электрон связан с каким-то конкретным атомом. Когда присутствие других атомов изменяет потенциальную яму отдельного атома (рис.5, рис.6), результирующий кулоновский потенциал уже не будет удерживать 3S – электроны около конкретных атомов, так что они могут находиться в твердом теле где угодно в результате перекрытия волновых функций 3S – электронов. Но 3S – электроны не могут свободно покидать твердое тело, так как их волновые функции не «выходят» за пределы вещества. Энергия связи электронов в твердом теле равна работе выхода φ.

Твердое тело из четырех атомов будет иметь всего четыре уровня, распределенные по некоторому энергетическому интервалу.

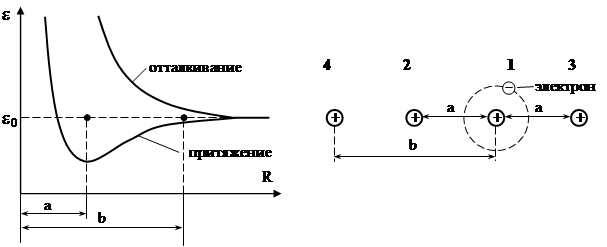
Рис.8

Например: в основном состоянии атома водорода электрон может находиться в одном из двух состояний – со спином вверх или вниз. В системе четырех протонов имеется восемь возможных состояний. Но если добавить еще три электрона, чтобы получить четыре атома водорода, то занятыми окажутся четыре состояния и на каждый электрон будет приходиться по два состояния. Эффект сближения атомов проявляется в изменении энергии отдельных состояний

где - энергия изолированного атома, - изменения энергии, связанные с влиянием соответствующих протонов 2, 3, 4. R – расстояние между атомами.

Эффект сближения атомов проявляется в увеличении общего числа уровней. В реальном теле содержится порядка 10²³ отдельных уровней, которые непрерывно распределяются внутри некоторого интервала, образуя зону разрешенных значений энергии (рис.9). Такая же ситуация в основном имеет место для валентных электронов любого атома.

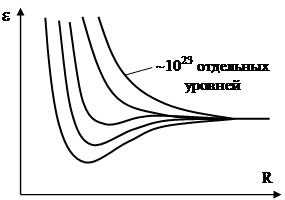Рис.9

В твердом натрии зона 3S – электронов является внешней, наполовину заполненной. Верхняя граница заполненных уровней приходится на середину зоны. Электрон может перейти на более высокий свободный уровень в этой зоне за счет теплового или электрического возбуждения. Следовательно, твердый натрий обладает хорошей электропроводностью и теплопроводностью. На рис.10 зонная структура проводников (натрия). Верхняя зона – частично заполненная зона. Нижние зоны - заполненные электронами.

Если число энергетических уровней в зоне больше числа электронов в ней, то электроны легко возбуждаются, обеспечивая тем самым проводимость, если же все уровни в зоне заполнены, то проводимость невозможна или затруднена.

Например: в кремнии, германии, углероде (алмаз) на P – оболочке имеются два электрона и возникает смешанная конфигурация S и P – орбиталей (орбиталь – волновая функция, описывающая данное квантовое состояние), которая делает особенно благоприятной конфигурацию из четырех атомов, изображенную на рис.11 (энергия кулоновского отталкивания электронов минимальна).

Рис.11

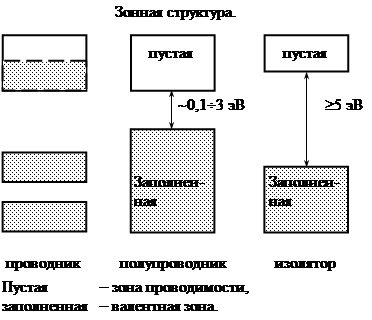
Волновые функции S и P – электронов образуют одну совершенно пустую гибридную SP – зону и одну заполненную гибридную SP – зону. Заполненная и пустая зоны разделены довольно значительным энергетическим интервалом или зоной запрещенных значений энергии. Для изоляторов типичное значение ширины запрещенной зоны ~ 5 эв и больше. Ширина запрещенной зоны для полупроводников (германия 0,67 эв, кремния 1,12 эв) находится в пределах 0,1 ¸ 3 эв.

Полупроводники и изоляторы отличаются друг от друга только шириной запрещенной зоны.

Рис.12

§ Теорема Блоха

Теорема Блоха утверждает, что собственные функции волнового уравнения с периодическим потенциалом имеют вид произведения функции плоской волны

На функцию , которая является периодической функцией в кристаллической решетке:

Индекс в указывает, что эта функция зависит от волнового вектора .

Волновую функцию называют функцией Блоха. Решения уравнения Шредингера такого вида состоят из бегущих волн, из таких решений можно составить волновой пакет, который будет представлять электрон, свободно распространяющийся в периодическом потенциальном поле, созданном ионными остовами.

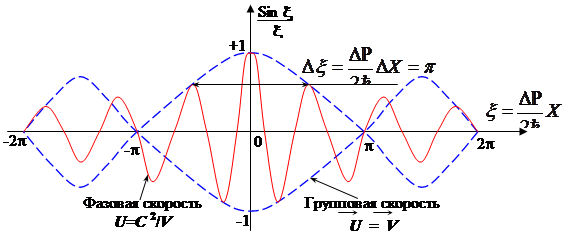
Рис.13

Форма волнового пакета при t=0 для дебройлевских волн 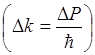. Амплитуда указана штриховой линией, волна – сплошной. Движение монохроматической плоской волны вдоль оси Х можно описать функцией

(1)

Скорость распространения волны может быть найдена как скорость перемещения постоянной фазы.

(2)

Если время изменится на величину ∆t, то для того, чтобы соблюдалось условие (2), координата должна измениться на величину ∆х, которая может быть найдена из равенства

т.е. (3)

Отсюда скорость распространения постоянной фазы, получившей название фазовой скорости:

(4)

Фазовая скорость фотонов (m₀ = 0) равна скорости света

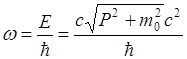(5)

, (6)

Фазовая скорость электрона, движущегося со скоростью V, можно написать

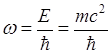
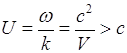(7)

, (7)

т.е. она становится больше скорости света, поскольку V< с. Это говорит о том, что фазовая скорость не может соответствовать движению частицы или же переносу какой-либо энергии.

Реальный процесс не может быть чисто монохроматическим (k = const). Он всегда обладает определенной шириной, т.е. состоит из набора волн, обладающих близкими волновыми числами, а вместе с тем и частотами.

С помощью набора волн можно построить волновой пакет, амплитуда которого отлична от нуля лишь в небольшой области пространства, которую связывают с местоположением частицы. Максимум амплитуды волнового пакета распространятся со скоростью, которая получила название групповой скорости.

Амплитуда В волнового пакета

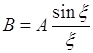
где A – амплитуда постоянная каждой из этих волн.

В распространяется со скоростью

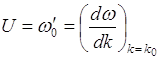
Для фотонов (m₀ = 0)

Для дебройлевских волн

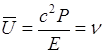
т.е. групповая скорость совпадает со скоростью движения частицы.

В точках и т.д.

Квадрат амплитуды обращается в нуль.

Область локализации волнового пакета

,

где - ширина волнового пакета.

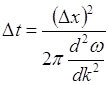
где - время расплывания волнового пакета.

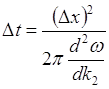
Соотношения неопределенностей Гейзенберга. Чем меньше , тем шире . Для монохроматической волны

,

где амплитуда во всем пространстве имеет одно и то же значение, т.е. наложение частицы (одномерный случай) во всем пространстве равновероятно. Это обобщается и на трехмерный случай.

Для нерелятивистского случая (m = m₀) время расплывания волнового пакета

если m = 1г, ,то

время расплывания чрезвычайно велико. В случае электрона m₀ ~ 10^-27г (размеры атома),

т.е. для описания электрона в атоме мы должны использовать волновое уравнение, т.к. волновой пакет расплывается практически мгновенно.

Волновое уравнение фотона содержит вторую производную по времени, т.к. фотон всегда релятивистская частица.

Движение электрона в кристалле

Закон движения, сравнивая с

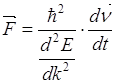где

где m* - эффективная масса, она учитывает совместное действие потенциального поля и внешней силы на электрон в кристалле.

- в зоне проводимости,

в валентной зоне

- в валентной зоне, но в зоне германия и кремния имеются тяжелые и легкие дырки. Эффективные массы всегда выражаются в долях истинной массы m₀ = 9·10^-28г

и

Эффективная масса – тензорная величина, в различных направлениях она различна, что является следствием анизотропных свойств кристаллов.

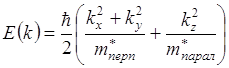
Е_к – уравнение эллипсоида вращения и описывается двумя значениями масс и

Энергетический спектр электронов и дырок в координатах Е и K

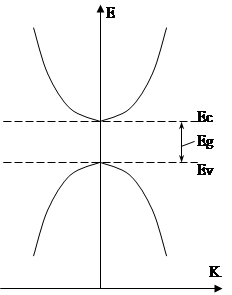Е(К) – функция квазиимпульса. Энергия электрона в идеальной решетке есть периодическая функция квазиимпульса.

Импульс электрона

Дырки – квазичастицы с меньшей энергией располагаются у потолка валентной зоны и увеличивают свою энергию, перемещаясь по шкале энергии вглубь валентной зоны. Для дырок и электронов отсчет энергий в противоположных направлениях.

Электроны и дырки, обладающие волновым вектором , могут сталкиваться с другими частицами или полями, как если бы они имели импульс

- называется квазиимпульсом.

Обозначение	Название	Поле
	Электрон	-
	Фотон	Электромагнитная волна
	Фонон	Упругая волна
	Плазмон	Коллективная электронная волна
	Магнон	Волна перемагничивания
---	Полярон	Электрон + упругая деформация
---	Экситон	Волна поляризации

На фононах рассеиваются рентгеновские лучи, нейтроны.

Импульсу в квантовой механике отвечает оператор .

т.е. плоская волна Ψ_к является собственной функцией оператора импульса , причем собственными значениями оператора импульса служат

Энергия Ферми определяется как энергия электронов на высшем заполненном уровне

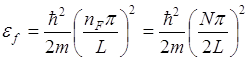
где n_F – квантовое число наивысшего занятого энергетического уровня.

2n_F=N

где N – число электронов в объеме

Энергия - квадратичная функция квантового числа n_F.

Волновые функции, удовлетворяющие уравнения Шредингера, для свободной частицы в периодическом поле представляют собой бегущие плоские волны:

при условии, что компоненты волнового вектора принимают значения

аналогичные наборы для K_y и K_z. Любая компонента вектора имеет вид

, где

n – целое положительное или отрицательное число. Компоненты являются квантовыми числами наряду с квантовыми числами

задающим направление спина.

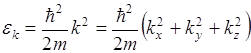
т.е. собственные значения энергии состояний с волновым вектором

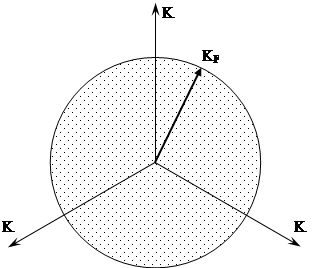В основном состоянии (1S) системы из N свободных электронов занятые состояния можно описывать точками внутри сферы в К – пространстве. Энергия, соответствующая поверхности этой сферы, является энергией Ферми. Волновые векторы, «упирающиеся» в поверхность этой сферы, имеют длины, равные K_F, а сама поверхность называется поверхностью Ферми (в данном состоянии она является сферой). K_F- радиус этой сферы

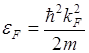
где – энергия электрона с волновым вектором , оканчивающимся на поверхности сферы.

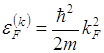
Каждой тройке квантовых чисел K_x, K_y, K_z отвечает элемент объема в К – пространстве величиной 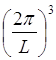. поэтому в сфере объемом число точек, описывающих разрешенные состояния, равно числу ячеек объемом 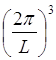, и поэтому число разрешенных состояний равно

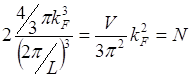
где множитель 2 в левой части учитывает два допустимых значения спинового квантового числа

()

для каждого разрешенного значения

Полное число состояний равно числу электронов N.

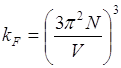
Радиус сферы Ферми K_Fзависит лишь от концентрации частиц и не зависит от массы m

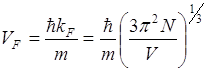
Энергию Ферми можно определять как энергию таких квантовых состояний, вероятность заполнения которых частицей равна 1/2.

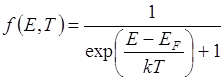
если Е=Е_F, то

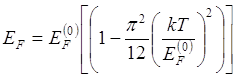значение ее можно рассчитать при Т=0 по формуле

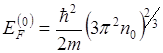
Но абсолютный нуль температуры понимается как предел

Т ® 0,

имея в виду, что абсолютный нуль не достижим и плюс принцип Паули.

Обычно рассматриваются системы не только при Т = 0, но и при любой температуре, если граничная энергий , это условие вырождения, функция распределения таких частиц близка к «ступеньке»

Для таких систем, где можно пренебречь зависимостью Е_F от температуры и считать

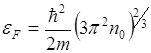
Существуют таблицы параметров поверхности Ферми для ряда металлов, вычисленных для модели свободных электронов для комнатной температуры (Т = 300⁰К).

Концентрация электронов определяется произведением валентности металла на число электронов в 1 см³.

то получим:

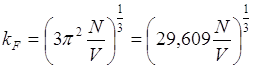
или, если ,

Например: Li

Валентность – 1,

*r₀ – радиус сферы, содержащей один электрон.

L_н – боровский радиус 0,53×10^{-8 см.}

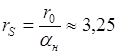* безразмерный параметр

Волновой вектор К_F = 1,11×10⁸ см^-1;

Скорость Ферми V_F = 1,29×10⁸ см/с;

Энергия Ферми .

Температура Ферми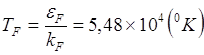

Т_F не имеет никакого отношения к температуре электронного газа.

Определим – число состояний на единичный энергетический интервал, части называемый плотностью состояний при

;

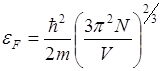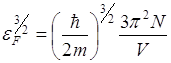
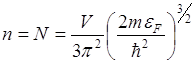
Плотность состояний равна:

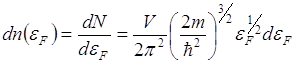
Вариант 5 № 2. Число электронов с кинетической энергией от Е_F/2 до Е_F определяется соотношением

По аналогии:

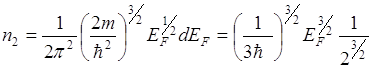
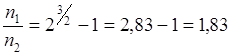
Этот же результат можно получить из

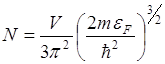
в более простой форме:

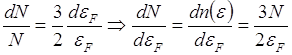
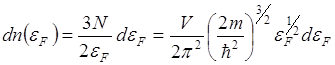
С точностью порядка единицы число состояний на единичный энергетический интервал вблизи энергии Ферми равно отношению числа электронов проводимости к энергии Ферми.

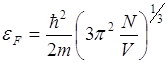
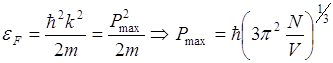
Выводы

1. Эффективные массы: германий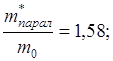

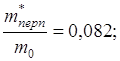
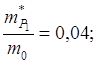
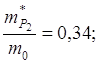
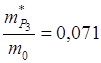
кремний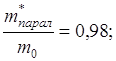

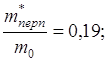
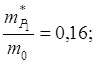
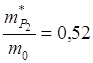
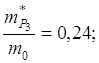
т.е. в валентной зоне германия и кремния имеются тяжелые и легкие дырки. Валентные зоны состоят из трех подзон.

2. Поверхность Ферми есть поверхность постоянной энергии в пространстве. Поверхность Ферми при абсолютном нуле отделяет заполненные электронами состояния от незаполненных состояний. Сфера Ферми. Все состояния с К<К_F являются занятыми.

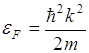
3. Разнообразие свойств твердых тел и есть свидетельство разнообразия квазичастиц.

4. До последнего времени считалось, что электроны похожи друг на друга. Когда хотят подчеркнуть отличие электронов железа от электронов меди, то говорят, что они обладают различными поверхностями Ферми.

На всемирной выставке в Брюсселе здание отдает дань веку физики. Представляет правильную систему связанных между собой сфер, внутри которых выставочные помещения. Каждая из которых (сфера) представляет ион железа, потерявший одни электрон. Это поверхность уровня Ферми.

У каждого металла только своя ему присущая форма поверхности Ферми, она ограничивает область импульсного пространства, занятого электронами проводимости при абсолютном нуле. Это визитные карточки различных металлов.

5. Свойства металлов определяются электронами на поверхности Ферми или вблизи нее.

6. Движение волнового пакета, связанного с волновым вектором описывается уравнением

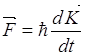
Групповая скорость

§ Энергетический спектр энергии для свободных электронов в периодическом поле

На рисунке заштрихованные области запрещенных значений энергии (энергетические щели).

Волновая функция имеет вид:

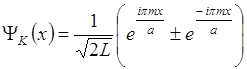
Энергия не является теперь непрерывной функцией квазиимпульса , она непрерывна только в зонах разрешенных энергий и претерпевает разрывы на границах зон Бриллюэна. Энергетические зоны являются следствием периодической структуры кристалла и представляют собою фундаментальные характеристики электронной структуры твердого тела. – граница зоны, это вектор обратной решетки.

Области значений , при которых энергия электронов изменяется непрерывно, а на границах претерпевает разрыв, называются зонами Бриллюэна.

Энергетический спектр электронов и дырок в координатах Е – К. В германии и кремнии зона проводимости описывается двумя значениями масс.

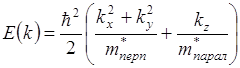
§ Механизм электропроводности собственного полупроводника

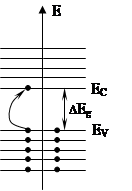
Содержащую электроны зону с наибольшей энергией, называют валентной зоной. Первую зону с незанятыми энергетическими уровнями называют зоной проводимости, так как электроны в этой зоне участвуют в переносе заряда. В проводниках валентная зона и зона проводимости либо совпадают, либо перекрываются. В изоляторах и полупроводниках эти зоны отделены друг от друга.

Если материал находится не в состоянии основном, а обладает дополнительной энергией – тепловым возбуждением. Эта энергия играет важную роль в свойствах электропроводности.

Проводник в основном состоянии, если отсутствует тепловая энергия т.е. Т = 0. Зависимость вероятности заполнения электронами энергетических уровней при КТ = 0 от энергии e отсчитывается от дна зоны.

для всех значений энергии, соответствующих заполненным уровням.

Энергия, отсчитываемая от дна зоны, при которой величина f(E) скачком изменяется от 1 до 0, называется энергией Ферми e_F В данном случае т.е. работе выхода

При наличии тепловой энергии некоторые электроны возбудятся и перейдут из первоначальных состояний на свободные энергетические уровни. Для электронов с энергией вблизи e_F такие переходы более вероятны, так как требуется меньшая энергия возбуждения. Соответственно, и вероятность заполнения состояний уменьшается с ростом их энергии. Если электроны не подчиняются принципу Паули, то их распределение по энергии описывается классическим распределением Максвелла – Больцмана

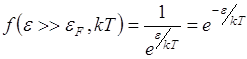Распределение, учитывающее принцип Паули, называется распределением Ферми – Дирака

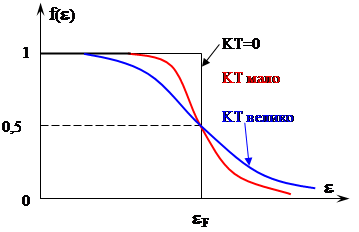
Распределение Ферми – Дирака при различных значениях КТ показано на рисунке. Здесь энергия Ферми имеет смысл энергии уровня, которому отвечает 50%-ная вероятность заполнения.

Число свободных уровней (вакансий) ниже уровня Ферми, и их распределение относительно e_F совпадает с числом и распределением заполненных состояний выше уровня Ферми. Эти состояния отвечают тепловому возбуждению электронной системы и обеспечивают появление кинетической энергии направленного движения. С ростом температуры (увеличение КТ) уменьшается наклон кривой f(e) вблизи e_F и увеличивается вероятность заполнения состояний с большими энергиями.

Из выражений для f(E, K, T) видно, что проводимость материалов сильно зависит от температуры.

В полупроводниках положение уровня Ферми соответствует формально потолку валентной зоны, но это неверно. Пусть с потолка валентной зоны (с энергией e_V) отдельный электрон от возбуждения перешел на дно (с энергией e_C) пустой зоны проводимости.

e_V – потолок валентной зоны

e_C – дно зоны проводимости.

На рисунке уровень Ферми находится в середине запрещенной зоны, учитывая симметрию распределения Ферми – Дирака относительно энергии Ферми e_F и очевидную симметрию функции f(E) в промежутке между потолком валентной зоны и дном зоны проводимости.

* Определим вероятность перехода электрона в зону проводимости для алмаза, ширина запрещенной зоны e_g»5,5 эв. при комнатной температуре КТ = 0,026 эв. для дна зоны проводимости

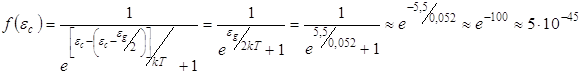
Таким образом, вряд ли даже один из каждых 10⁴⁴ электронов в валентной зоне будет иметь энергию, достаточную для перехода в зону проводимости при комнатной температуре. Поскольку каждый моль вещества содержит около 10²⁴ атомов. Следовательно, алмаз – хороший изолятор.

Определим для вероятность при КТ = 0,026 эв. (комнатная)

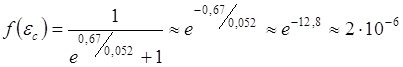
В этом случае приблизительно один валентный электрон из миллиона может при возбуждении перейти на дно зоны проводимости и в зоне проводимости можно найти электроны.

Их будет значительно меньше, чем в случае проводника, у которого f(e) в зоне проводимости составляет порядка единицы. Однако в зоне проводимости полупроводника все же имеется достаточно электронов и они вносят вклад в электропроводность полупроводника. В полупроводниках f(e) сильно зависит от температуры. Возрастание температуры на 10⁰К относительно комнатной (300⁰К) т.е. всего на 3% вероятность перехода электронов в зону проводимости увеличивается приблизительно на 30%. С уменьшением ширины запрещенной зоны чувствительность полупроводников к температуре возрастает.

Возбуждаясь с переходом в зону проводимости, электроны оставляют после себя в валентной зоне незанятые состояния или «дырки». Заполненная первоначально валентная зона становится частично заполненной и, следовательно, в ней возможны энергетические возбуждения электронов, хотя очень небольшого числа. Дырка ведет себя подобно положительно заряженной частице, которая может участвовать в электрической проводимости. Реальному движению электронов соответствует более или менее свободной фиктивное движение дырок в направлении внешнего электрического поля.

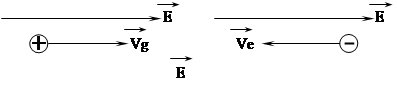
Дырки реагируют на внешнюю силу (например, на внешнее электрическое поле) не так, как свободные электроны, поэтому, чтобы учесть влияние других атомов на подвижность дырок, им приписывают эффективную массу m*, которая немного больше эффективной массы электрона.

Плотность тока электронов и дырок

где n – концентрация электронов,

р – концентрация дырок,

m_n – подвижность электронов,

m_p – подвижность дырок.

Под действием внешнего электрического поля электроны и дырки приобретают скорости направленного движения, дрейфовые скорости

m_nи m_др - подвижности

Для собственных полупроводников n=p

или

где , s - коэффициент

n – сильно зависит от температуры в зоне проводимости, в то время как подвижности слабо зависят от температуры

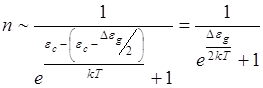
Если концентрация электронов в зоне проводимости мала, то вероятность заполнения каждого уровня мала по сравнению с единицей в знаменателе, то ею можно пренебречь.

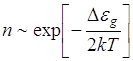и следовательно , или

Электропроводность собственных полупроводников возрастает с температурой, у проводников уменьшается.

Если прологарифмировать 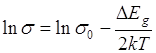и построить график зависимости lns от , то получим прямую линию, угловой коэффициент которого равен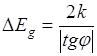

Это дает возможность, измеряя электропроводность полупроводника при различных температурах, определить опытным путем ширину запрещенной зоны для данного полупроводника

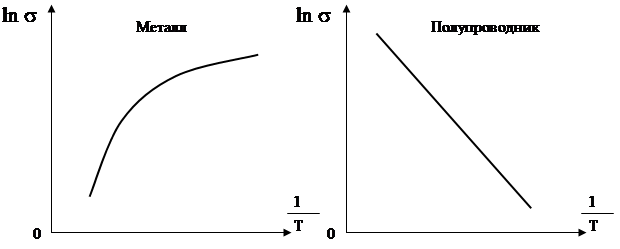
Для металлов с ростом температуры сопротивление увеличивается

R₀ –сопротивление при t = 0⁰С

R_t – сопротивление при t⁰С

a – термический коэффициент сопротивления, равный 1/273

Для металлов

Для полупроводников сопротивление с ростом температуры быстро уменьшается или где КВ=Е_a, то

где E_a – энергия активизации, она различна для разных интервалов температур.

Наличие энергии активации E_a означает, что для увеличения проводимости к полупроводниковому веществу необходимо подвести энергию. Полупроводники – это вещества, проводимость которых сильно зависит от внешних условий: температуры, давления, внешних полей, облучения ядерными частицами.

Полупроводники – это вещества, имеющие при комнатной температуре удельную электрическую проводимость в интервале от