Моделі систем масового обслуговування. Класифікація систем масового обслуговування
РЕФЕРАТ
На тему:
«Моделі систем масового обслуговування. Класифікація систем масового обслуговування»
Математичне введення в теорію ланцюгів Маркова. (Markov’s chain)
Дискретні ланцюги Маркова. Говоритимемо, що заданий дискретний ланцюг Маркова, якщо для послідовності випадкових величин виконується рівність ![]() .
.
Це означає, що потік випадкових величин визначається тільки вірогідністю переходу від попереднього значення випадкової величини до подальшого. Знаючи початковий розподіл вірогідності, можна знайти розподіл на будь-якому кроці. Величини in можна інтерпретувати як номери станів деякої динамічної системи з дискретною безліччю станів (типу кінцевого автомата). Якщо вірогідність переходів не залежить від номера кроку, то такий ланцюг Маркова називається однорідним і її визначення задається набором вірогідності ![]() .
.
Для однорідного Марківського ланцюга можна визначити вірогідність переходу із стану i в стан j за m кроків
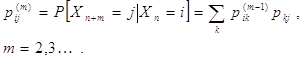
Ланцюг Маркова називається тією, що не приводиться, якщо кожний її стан може бути досягнутий з будь-якого іншого стану. Стан i називається поглинаючим, якщо для нього pii=1.
Стан називається поворотним, якщо вірогідність попадання в нього за кінцеве число кроків рівна одиниці. В іншому випадку стан відноситься до неповоротних. Поворотний стан може бути періодичним і аперіодичним залежно від наявності кратних кроків повернення. Введемо вірогідність повернення в стан i через кроків після відходу з цього стану: ![]()
Вони дозволяють визначити середнє число кроків або, інакше кажучи, середній час повернення:![]() .
.
Стан називається поворотним нульовим, якщо середній час повернення в нього рівно нескінченності, і поворотним ненульовим, якщо цей час звичайно. Відомі дві важливі теореми:
Теорема 1
Стани ланцюга Маркова, що не приводиться, або всі неповоротні, або всі поворотні нульові, або всі поворотні ненульові. У разі періодичного ланцюга всі стани мають один і той же період.
Друга теорема розглядає вірогідність досягнення станів в стаціонарному (тобто не залежному від початкового розподілу вірогідності) режимі. Відповідний розподіл вірогідності також називають стаціонарним. Знаходження стаціонарного розподілу вірогідності досягнення станів одна з основних задач теорії телетрафіка.
Теорема 2
Для ланцюга Маркова, що не приводиться і аперіодичної, завжди існує гранична вірогідність, не залежна від початкового розподілу вірогідності. Більш того, має місце одна з наступних двох можливостей:
А) всі стани ланцюга неповоротні або всі поворотні нульові, і тоді вся гранична вірогідність рівна нулю і стаціонарного стану не існує;
Б) всі стани поворотні ненульові і тоді існує стаціонарний розподіл вірогідності:
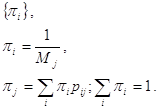
Стан називається ергодичним, якщо воно аперіодичне і поворотно-ненульове. Якщо всі стани ланцюга Маркова ергодичні, то весь ланцюг називається ергодичним. Граничну вірогідність ергодичного ланцюга Маркова називають вірогідністю стану рівноваги, маючи на увазі, що залежність від початкового розподілу вірогідності повністю відсутня.
Ланцюг Маркова з кінцевим числом станів (кінцевий ланцюг), зручно зображати у вигляді орієнтованого графа, званого діаграмою переходів. Вершини графа асоціюються із станами, а ребра з вірогідністю переходів.
Обчислення вірогідності досягнення станів проводиться прямими методами або за допомогою z-преобразування.
Ланцюг Маркова
Введемо матрицю вірогідності переходів і вектор-рядок вірогідності на кроці n
![]() .
.
Розподіл вірогідності на довільному кроці тоді підкорятиметься матричному співвідношенню:
![]() .
.
Воно дозволяє рекуррентно обчислювати всю вірогідність станів. Для знаходження граничного розподілу (стаціонарного) потрібно вирішити рівняння:
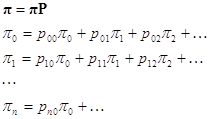
Його можна вирішувати як систему лінійних рівнянь алгебри, якщо ланцюг кінцевий.
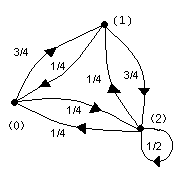
Для прикладу (мал. 1) маємо:
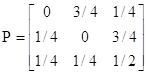 .
.
і рішення матричного рівняння зводиться до рішення системи трьох рівнянь:
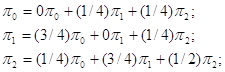
Коефіцієнти першого рівняння в цій системі доповнюють до одиниці суму коефіцієнтів другого і третього рівнянь; це свідчить про лінійну залежність між ними. Тому для вирішення системи рівнянь потрібно ввести додаткову нормуючу умову. В даному прикладі: ![]() .
.
Вирішуючи систему отриманих рівнянь, маємо:
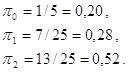
Рівняння для вірогідності досягнення стану в перехідному режимі вирішити значно важче. Деякого спрощення можна досягти, використовуючи z – перетворення. Застосуємо його до рівняння для перехідної вірогідності
![]() .
.
Позначаючи відповідні перетворення, отримаємо: ![]() .
.
Всі отримані тут математичні результати відносилися до однорідних Марківських процесів, де вірогідність переходів не залежить від часу. В більш загальному випадку така залежність має місце.
Розглянемо вірогідність переходу системи із стану i на m-том кроці в стан j на n-том кроці для n > m.
Можна показати, що ця вірогідність зв'язана між собою, так званим рівняннями Чепмена-Колмогорова. (Chapman – Kolmogorov)
![]() .
.
Для однорідних ланцюгів Маркова ці рівняння спрощуються оскільки
![]() .
.
І зводяться до аналізованих вище.
Безперервні ланцюги Маркова
Випадковий процес X(t) з дискретною безліччю значень утворює безперервний ланцюг Маркова, якщо
![]() .
.
Майбутні стани залежать від минулого тільки через поточний стан. Для безперервний ланцюгів Маркова основним також є рівняння Чепмена – Колмогорова, для однорідного ланцюга має вигляд: ![]() .
.
Тут матриця H(t)= (pij(t)) – матриця вірогідності переходу із стану i в стан j у момент часу t, а матриця Q називається «матрицею интенсивностей переходів». Її елементи мають наступний сенс: якщо у момент часу t система знаходилася в стані Ei, то вірогідність переходу протягом проміжку часу (t,t+Дt) в довільний стан Ej задається величиною qij(t)Дt + о(Дt), а вірогідність відходу із стану Ei величиною -qiiДt + про(Дt).
Таким чином, інтенсивності переходів можна обчислювати як відповідні межі при прагненні до нуля тривалості тимчасового інтервалу.
Найважливішим для подальшого використовування є клас безперервних ланцюгів Маркова званих «процесами загибелі – розмноження» (Birth – death process). Для таких систем із стану до можливі переходи тільки в стани до, k‑1 і k+1 в наступні моменти часу:
· у момент t об'єм популяції був рівний до і протягом часу (t, t+Дt) не відбулося зміни стану
· у момент t об'єм популяції був рівний k‑1 і протягом часу (t, t+Дt) народився один член популяції
· у момент часу t об'єм популяції був рівний k+1 і протягом часу (t, t+Дt) загинув один член популяції.
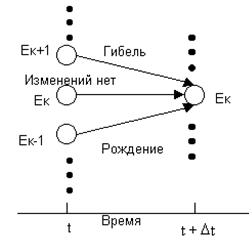
Мал. 1. Можливі переходи в стан Тіньк
Шукатимемо вірогідність того, що у момент часу t об'єм популяції рівний до, позначивши його Pk(t). Можна записати співвідношення для вірогідності досягнення стану до у момент часу t+Дt.
![]() .
.
Визначимо граничні і нормуючі умови:
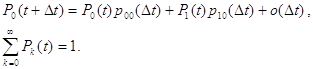
Виразимо вірогідність переходів за інтервал Дt через інтенсивності
Віри(+1)=лkДt+o(Дt); Віри(-1)=мkДt+o(Дt).
Вірогідність нуля народжень 1 – лkДt+o(Дt), а нуля загибелі 1 – мkДt+o(Дt).
Таким чином, вірогідність того, що стан до збережеться незмінним, буде рівна твору (1 – лkДt+o(Дt)) (1 – мkДt+o(Дt)).
Тоді рівняння Чепмена-Колмогорованабувають вигляд
![]()
Розкриваючи дужки і проводячи розподіл на Дt, отримаємо:
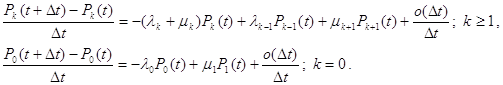
В межі виходить система диференціально-різницевих рівнянь, рішення якої гратимуть важливу роль для практичних задач.
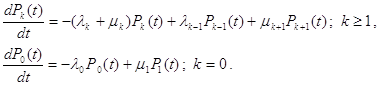
У відповідність цій системі рівнянь можна поставити наочну діаграму интенсивностей переходів, яка аналогічна діаграмі переходів для дискретних ланцюгів Маркова (Мал. 2)
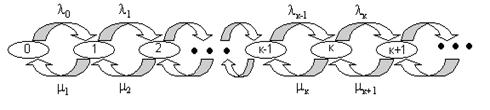
Мал. 2. Діаграма интенсивностей переходів для процесу розмноження і загибелі
Овалам тут відповідають дискретні стани, а стрілки визначають інтенсивності потоків вірогідності (а не вірогідність!) переходів від одного стану до іншого.
Має місце своєрідний «закон збереження»:
Різниця між сумою интенсивностей, з якою система потрапляє в стан до і сумою интенсивностей, з якою система покидає цей стан повинна дорівнювати інтенсивності зміни потоку в цей стан (похідної за часом).
Застосування закону збереження дозволяє одержувати рівняння для будь-якої підсистеми Марківського ланцюга типу процесу «загибелі-розмноження. Особливо ефективною виявляється побудова рішень в стаціонарному, сталому режимі, коли можна вважати що вірогідність в довільний, достатньо віддалений момент часу, залишаються постійними.
Прирівнюючи похідну за часом нулю, одержуємо систему різницевих рівнянь
![]()
Вважаючи, що інтенсивності л‑1 =л-2 = л‑3 =.0; м0 = м‑1 = м‑2 = м‑3=.=0, друге рівняння виписувати не буде окремо далі потрібно. Отже, стаціонарний режим в ланцюзі Маркова описуватиметься системою різницевих рівнянь і умовою нормування для вірогідності
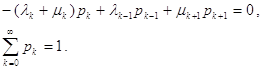
Неважко бачити, що ці рівняння легко виводяться із закону збереження интенсивностей вірогідності. В стаціонарному режимі різниця потоків рівна нулю і отримані вище рівняння придбавають значення рівнянь рівноваги або балансу, як їх і називають.
![]() .
.
Інтенсивність потоку вірогідності в стан до рівна інтенсивності потоку з цього стану.
Вирішувати рівняння балансу можна, спочатку визначивши при до =0 значення
![]() .
.
Потім, побудувавши систему рівнянь для до =1, можна отримати
![]() .
.
Далі одержуємо
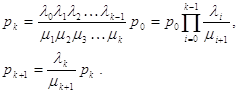
З умови нормування: 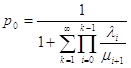 .
.
Система, описувана отриманими вище виразами, матиме стаціонарну вірогідність станів, коли вона ергодична. Ця умова може бути виражений через співвідношення интенсивностей. Необхідно і достатньо, щоб існувало деяке значення до, починаючи з яким виконувалася нерівність
![]() .
.
Для більшості реальних систем масового обслуговування ця нерівність виконується.
Класифікація систем масового обслуговування
Використовується трьох -, чотирьох -, шести – компонентне символічне позначення системи масового обслуговування, запропоноване Кендаллом (Candall) і розвинуте в роботах Г.П. Барашина.
а/b/c:d/e/f
а – розподіл потоку запитів, що поступає.
b – закон розподілу часу обслуговування.
Типові умовні позначення:
М – експоненціальний (Марківське) розподіл
D – детермінований розподіл
Тіньк – ерланговський розподіл к-го порядку
HMk – гиперекспониціональне
HEk – гиперерлангівське розподіл порядку до
GI – довільний розподіл незалежних проміжків між заявками
G – довільний розподіл тривалостей обслуговування.
з – структура системи обслуговування (звичайно число серверів).
d – дисципліна обслуговування (параметри після двокрапки іноді опускають).
Звичайно використовується скорочене символічне позначення, наприклад FF замість FIFO, LF, PR і т. п.
e – максимальне число запитів, сприймане системою, може вживатися символ ¥.
f – максимальне число запитів до системи обслуговування.
В деяких публікаціях останніми символами відображають якісні характеристики системи обслуговування. Деякі загальні результати і основи математичного апарату, необхідного для аналізу можна отримати, розглядаючи системи G/G/m.
Формула Літтла (Little)
Розглянемо тимчасову діаграму роботи системи масового обслуговування (мал. 3), відобразити на ній послідовність надходження вимог, приміщення вимог в чергу і обробки серверами системи.
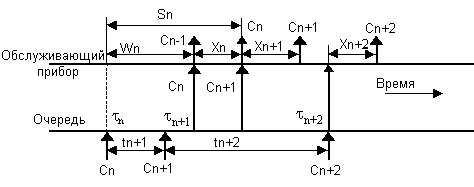
Тимчасова діаграма роботи системи масового обслуговування.
В загальному випадку ясно, що із збільшенням числа вимог росте час очікування. Встановимо співвідношення між середнім числом вимог в системі, інтенсивністю потоку і середнього часу перебування в системі. Позначимо число поступають в проміжку часу (0, t) вимог як функцію часу б(t).
Число витікаючих з системи заявок (обслужених) на цьому інтервалі позначимо д(t). На малюнку 4 показані приклади функціональної залежності цих двох випадкових процесів від часу.
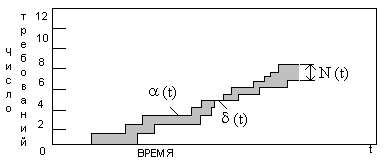
Мал. 4. Залежність між середнім числом вимог в системі, інтенсивністю потоку і середнім часу перебування в системі
Число вимог, що знаходяться в системі у момент t буде рівний:
![]() .
.
Площа між двома даними кривими від 0 до t – дає загальний час, проведений всіма заявками в системі за час t.
Позначимо цю накопичену величину г(t). Якщо інтенсивність вхідного потоку рівна л, а середня інтенсивність за час t: ![]() , той час, проведений однією заявкою в системі, усереднене по всіх заявках буде рівне:
, той час, проведений однією заявкою в системі, усереднене по всіх заявках буде рівне:
![]() .
.
Нарешті, визначимо середнє число вимог в системі в проміжку (0, t): ![]() .
.
З останніх трьох рівнянь виходить, що: ![]() (де
(де ![]() ).
).
Якщо в СМО існує стаціонарний режим, то при t>?, матимуть місце співвідношення:
![]()
![]()
Останнє співвідношення означає, що середнє число заявок в системі рівно твору інтенсивності надходження вимог в систему на середній час перебування в системі. При цьому не накладається ніяких обмежень на розподіли вхідного потоку і часу обслуговування. Вперше доказ цього факту дав Дж. Литтл і це співвідношення носить назву формула Літтла.
Цікаво, що як СМО можна розглянути тільки чергу із заявок в буфері. Тоді формула Літтла придбаває інше значення – середня довжина черги рівна твору інтенсивності вхідного потоку заявок на середній час очікування в черзі: ![]() .
.
Якщо навпаки розглядати СМО тільки як сервери, то формула Літтла дає:
![]() ,
,
де ![]() – середнє число заявок в серверах, а
– середнє число заявок в серверах, а![]() – середній час обробки в сервері.
– середній час обробки в сервері.
У будь-якому випадку: ![]() .
.
Одним з основних параметрів, які використовуються при описі СМО, є коефіцієнт використовування (utilization factor). Це фундаментальний параметр, оскільки він визначається як відношення інтенсивності вхідного потоку до пропускної спроможності системи. Оскільки пропускна спроможність СМО містить m серверів може бути визначений як: ![]() , то коефіцієнт використовування може бути визначений як
, то коефіцієнт використовування може бути визначений як ![]() .
.
Неважко бачити, що коефіцієнт використовування рівний в точності інтенсивності навантаження, якщо СМО з одним сервером і в m раз менше для систем з m серверами. Величина коефіцієнта використовування рівна середньому значенню від частки зайнятих серверів і ![]() .
.
Якщо в СМО типа G/G/1 існує стаціонарний режим і можна визначити вірогідність того, що в деякий випадковий момент сервер буде вільний, то ![]() .
.