Історія математики Греції

Реферат

з математики

на тему:

"Історія математики Греції"

Протягом останніх сторіч другого тисячоріччя до н.е. у басейні Середземного моря й у прилягаючих до нього областях дуже багато чого змінилося в економіці і в політиці.

Бронзове століття перемінилося тим нашим століттям, що ми називаємо століттям заліза, і відбувалося це в неясний час переселень і воїн. Лише деякі подробиці відомі нам про цю революційну епоху, але ми знаємо, що до її завершення, приблизно близько 900р. до н. е., уже не було царства Міноса і Хетської держави, значно слабкішими стали Єгипет і Вавілон і на історичній сцені з'явилися нові народи. Найбільш видатними серед них були євреї, ассирійці, фінікійці і греки. Витиснення бронзи залізом означало не тільки переворот у військовій справі, але і прискорення росту економіки завдяки здешевленню засобів виробництва, і це уможливило більш діяльну участь широких шарів суспільства в справах економічного і суспільного значення.

Це позначилося у двох важливих нововведеннях:

заміні незручного письма Стародавнього Сходу легко доступним алфавітом;

веденні карбованої монети, що послужило пожвавленню торгівлі.

Наступив той час, коли культурні цінності вже не могли далі залишатися винятковим надбанням східного чиновництва.

Діяльність "морських розбійників" - так єгипетські тексти характеризують деякі народи, що переселялися - спочатку супроводжувалася чималими культурними втратами. Критська цивілізація зникла, єгипетське мистецтво занепало, наука Вавилону і Єгипту окостеніла на сторіччя. Немає ніяких математичних текстів цього перехідного періоду. Коли положення знову стало стійким, Стародавній Схід оправився, залишаючись в основному вірним традиції, але було розчищено місце для цивілізації цілком нового складу - грецької цивілізації.

Ті міста, що виникли на узбережжя Малої Азії й у самій Греції, уже не були адміністративними центрами країни зрошувального землеробства. Це були торгові міста, де феодали-землевласники старого укладу були приречені на поразку в боротьбі, що їм довелось вести з незалежним, отримавшими політичну самосвідомість класом купців. Протягом сьомого і шостого сторіч до н. е. це купецтво узяло верх, але йому довелося у свою чергу вступити в боротьбу з дрібними торговцями і ремісниками, з демосом.

Підсумком був розквіт грецького поліса, самоврядної міста-держави - нове соціальне явище, цілком відмінне від ранніх міст-держав Шумеру й інших країн Сходу. Найбільш значні з цих міст-держав, склалися в Іонії, на анатолійскому березі. Їхня зростаюча торгівля зв'язала їх із всім узбережжям Середземного моря, із Двуріччям, Єгиптом, зі Скіфією і навіть більш далекими країнами. Довгий час ведуче місце займав Мілет. Але і міста на інших берегах: Коринф, пізніше Афіни у власне Греції, Кротон і Гіарент в Італії, Сіракузи в Сицилії - ставали багатше і значніше. Новий суспільний уклад створив новий тип людини. Купець-мандрівник ніколи ще не користався такою незалежністю, і він знав, що вона добута в завзятій і жорстокій боротьбі. Він ніяк не міг розділяти устояні погляди Сходу. Він жив у період географічних відкриттів, порівнянних тільки з відкриттями західноєвропейського шістнадцятого сторіччя, він не визнавав ні абсолютного монарха, ні влади, що з'являє у виді охоронного божества. А крім того він міг користатися відомим дозвіллям завдяки своєму багатству і праці рабів. Він міг помізкувати про навколишній його світ. Відсутність цілком сталої релігії привело багатьох мешканців цих прибережних міст до містицизму, але це сприяло і протилежному - росту раціоналізму і науковому підходу.

Сучасна математика народилася в цій атмосфері іонійського раціоналізму - математика, що ставила не тільки східне питання "як?", але і сучасне, наукове питання "чому?". Відповідно до переказу батьком грецької математики є мілетський купець Фалес, у першій половині шостого століття Вавілон і Єгипет, що відвідав. Але якщо він навіть цілком легендарна фігура, то за нею коштує щось цілком реальне. Це - образ, що відповідає тим умовам, у яких закладалися основи не тільки сучасної математики, але і всієї сучасної науки і філософії. Спочатку греки займалися математикою, маючи одну основну мету - зрозуміти, яке місце займає у всесвіті людина у рамках деякої раціональної схеми. Математика допомогла знайти порядок у хаосі, зв'язати ідеї в логічні ланцюжки, знайти основні принципи. Вона була найбільш теоретичною з усіх наук.

Безсумнівно, що грецькі купці познайомилися зі східною математикою, прокладаючи свої торгові шляхи. Але люди Сходу майже не займалися теорією, і греки швидко знайшли це. Чому в рівнобедрених трикутниках два кути рівні? Чому площа трикутника дорівнює половині площі прямокутника при однакових підставах і висотах? Такі питання природно виникали в людей, що ставили подібні питання в області космології, біології і фізики.

На жаль, у нас немає першоджерел, що описують ранній період розвитку грецької математики. Уцілілі рукописи відносяться до епохи християнства й ісламу і їх тільки в малій мірі доповнюють замітки в єгипетських папірусах трохи більш раннього періоду. Усе-таки класична філологія дала можливість відновити тексти, що належать до четвертого сторіччя до н.е., і ми завдяки цьому маємо у своєму розпорядженні надійні видання Евкліда, Архімеда, Аполлонія й інших великих математиків античності. Але в цих текстах перед нами вже цілком розвита математична наука, і навіть за допомогою пізніших коментарів по них важко простежити хід історичного розвитку. Про епоху формування грецької математики приходиться судити, ґрунтуючись лише на невеликих фрагментах, що приводяться в більш пізніх добутках, і на окремих зауваженнях філософів і інших не строго математичних авторів. Дуже багато дотепності і праці було вкладено в критику текстів, завдяки чому удалося роз'яснити чимало темних місць у цьому ранньому періоді. Ця робота, пророблена такими дослідниками, як Поль Таннері (Tannery), Хіт (Т.L. Heath), Цейтен (Н. G. Zeuten), Франк (Е. Frank) і ін., дозволяє нам дати у відомій мері зв'язну, хоча в значній частині можливу картину грецької математики в епоху її формування.

У шостому сторіччі до н.е. на руїнах Ассірійської імперії виникла нова велика східна держава - Персія Ахеменідів. Вона завоювала міста Анатолії, але суспільний лад грецької метрополії пустив уже глибокі корені і його не можна було розтрощити. Перська навала була відбита в історичних битвах під Марафоні, Саламине і Платеє. Головним результатом грецької перемоги було розширення й експансія Афін. Тут у другій половині п'ятого сторіччя, при Періклі, вплив демократичних елементів увесь час зростало. Вони були рушійною силою економічної і військової експансії, і близько 430 р. вони зробили Афіни не тільки центром Грецької імперії, але і центром нової і зацікавленої цивілізації - золотого століття Греції.

В обстановці суспільної і політичної боротьби філософи і наставники викладали свої теорії і заодно нову математику. Вперше в історії група критично мислячих, "софістів", менш скована традицією, чим яка-небудь інша попередня їй група вчених, стала розглядати проблеми математичного характеру скоріше з метою з'ясування їхньої суті, чим заради користі.

Тому що такий підхід дозволив софістам дійти до основ точного мислення взагалі, було б надзвичайно повчально познайомитися з їхніми міркуваннями. До нещастя, від цього періоду дійшов лише один цільний математичний фрагмент, що належить іонійскому філософу Гіппократові з Хіоса. Математичні міркування в цьому фрагменті на дуже високому рівні, і досить типово те, що в ньому розглядається зовсім "непрактичний", але теоретично істотне питання про так званих луночок - плоскі фігури, обмежених двома круговими дугами.

Це питання - знайти площу таких луночок, у яких площа раціонально виражається через діаметр, - має пряме відношення до центральної проблеми грецької математики - квадратурі кола. Аналіз цієї проблеми в Гіппократа показує, що в математиків золотого століття Греції була упорядкована система плоскої геометрії, у якій у повному обсязі застосовувався принцип логічного висновку від одного твердження до іншого ("апагоге"). Були закладені основи аксіоматики, на що вказує назва приписуваної Гіппократові книги "Початку" ("Stoіcheіa"), назва всіх грецьких аксіоматичних трактатів, включаючи трактат Евкліда. Гіппократ досліджував площі плоских фігур, обмежених як прямими лініями, так і дугами окружності. Він учить, що площі подібних кругових сегментів відносяться, як квадрати стягуючих їхніх хорд. Він знає теорему Піфагора, а також відповідна нерівність для непрямокутних трикутників. Весь його трактат уже міг би бути віднесений до евклідової традиції, якби він не був старше Евкліда більш ніж на сторіччя.

Проблема квадратури кола - одна з "трьох знаменитих математичних проблем античності", що у цей період стали предметом дослідження.

Ці проблеми такі:

1) Трисекція кута, тобто поділ будь-якого заданого кута на три частини.

2) Подвоєння куба, тобто визначення ребра такого куба, що мав би обсяг, удвічі більший обсягу заданого куба (так звана делійська задача).

3) Квадратура кола, тобто перебування такого квадрата, площа якого дорівнює площі даного кругу.

Значення цих проблем у тім, що їх не можна точно вирішувати геометрично за допомогою кінцевого числа побудов прямих ліній і окружностей - це можна зробити тільки приблизно, - внаслідок чого ці , проблеми стали засобом для проникнення в нові області математики. У зв'язку з цими проблемами були відкриті конічні перетини, деякі криві третього і четвертого порядку і трансцендентна крива, названа квадратриссою. Ми не повинні з упередженням підходити до питанню про значення цих проблем через те, що інший раз вони з'являлися у виді анекдоту (дельфійські пророцтва і т.п. ). Не раз траплялося, що основної важливості питання викладали у виді чи анекдоту головоломки - згадаємо про яблуко Ньютона.

Математики різних епох, включаючи нашу, показали, який зв'язок існує між цими грецькими проблемами і сучасною теорією рівнянь, зв'язок, що торкається питання про області раціональності, алгебраїчні числа і теорію груп.

Ймовірно, від групи софістів, що до деякої міри були зв'язані з демократичним рухом, відмежувалася інша група філософів з математичними інтересами, що примикав до аристократичних об'єднань. Вони називали себе піфагорійцями на честь засновника цієї школи Піфагора, що, приблизно, був містиком, ученим і державним діячем аристократичної користі. Софісти в більшості підкреслювали реальність змін, піфагорійці прагнули знайти в природі і суспільстві незмінне. У пошуках вічних законів світу вони вивчали геометрію, арифметику, астрономію і музику. Найвидатнішим їхнім представником був Архіт з Тарента, що жив близько 400 р. до н.е. і школі якого, якщо ми приймемо гіпотезу Франка (Е. Frank), варто приписати велику частину "піфагорійської" математики. Арифметика піфагорійців була найвищою мірою спекулятивною наукою і мала мало загального із сучасної їй обчислювальною технікою Вавилона. Числа розбивалися на класи: парні, непарні, непарно-парні, непарно-непарні, прості і складені, зроблені, дружні, трикутні, квадратні, п’ятикутні і т, д. Деякі з найбільш цікавих результатів отримані для "трикутних чисел", що зв'язують арифметику і геометрію:

термін „квадратні числа” пішов від побудов піфагорійців:

Самі фігури значно старше, адже деякі з них ми знаходимо в неолітичній кераміці. Піфагорійці ж досліджували їхньої властивості, внесли сюди наліт свого числового містицизму і зробили числа основою своєї філософії всесвіт, намагаючись звести всі співвідношення до числового ("усі є число"). Крапка була "поміщеною одиницею".

Піфагорійцям були відомі деякі властивості правильних багатокутників і правильних багатогранників.

Вони показали, як заповнити площину системою правильних трикутників, чи квадратів, чи правильних шестикутників, а простір - системою кубів. Згодом Арістотель намагався доповнити це невірним твердженням, що простір можна заповнити правильними тетраедрами). Можливо, що піфагорійці знали правильний октаедр і додекаедр - останню фігуру тому, що кристали піриту, що знаходяться в Італії, мають форму додекаедра, а зображення таких фігур у орнаментах як магічний символ відноситься ще до часів етрусків. Вони належать до кельтських племен Центральної Європи початку епохи залізного віку ( 900 р. до н.е. ) і пізніше (пірит був джерелом заліза).

Що стосується теореми Піфагора, піфагорійці приписували її своєму наставнику і передавали, що він приніс у жертву богам сто биків на подяку. Ми вже бачили, що ця теорема була відома у Вавилоні часів Хаммураппі, але дуже можливо, що перший загальний доказ був отриманий у школі піфагорійців.

Найбільш важливим серед приписуваних піфагорійцям відкриттів було відкриття ірраціонального у виді непорівнянних відрізків прямої лінії. Можливо, що воно було зроблено в зв'язку з дослідженням геометричного середнього a:b = b:c, величиною, що цікавила піфагорійців і служила символом аристократії. Чому дорівнює геометричне середнє одиниці і двійки, двох священних символів? Це вело до вивчення відносини сторін і діагоналі квадрата, і було виявлено, що таке відношення не виражається "числом", тобто тим, що ми тепер називаємо раціональним числом (цілим чи числом дробом), а тільки такі числа допускалися піфагорійською арифметикою.

Припустимо, що це відношення дорівнює р : q, де цілі числа р и q ми завжди можемо вважати взаємно простими. Тоді р2 = 2q отже, р2, а з ним і р - парне число, і нехай р = 2r. Тоді q повинно бути непарним, але, тому що q2 = 2r2, воно повинно бути також парним. Таке протиріччя дозволялося не розширенням поняття числа, як на чи Сході в Європі епохи Відродження, а тим, що теорія чисел для таких випадків відкидалася, синтез же шукали в геометрії.

Це відкриття, що порушило невимушену гармонію арифметики і геометрії, імовірно, було зроблено в останні десятиліття п'ятого сторіччя до н.е.. Поверх того, виявилися інші труднощі - виявилася в розуміннях про реальність змін, і цим філософи займаються до наших днів. Відкриття цих нових труднощів приписують Зенонові Элейському (близько 450 р. до н.е. ), учню Парменіда, філософа-консерватора, що учив, що розум осягає тільки абсолютне буття і що зміна є тільки удаване. Це придбало математичне значення тоді, коли в зв'язку з такими задачами, як визначення обсягу піраміди, сталі займатися нескінченними процесами. Тут парадокси Зенона виявилися в протиріччі з деякими давніми й інтуїтивними представленнями відносно нескінченно малого і нескінченно великого. Завжди вважали, що суму нескінченно багатьох величин можна зробити як завгодно великий, навіть якщо кожна величина вкрай мала, а також що сума кінцевого чи нескінченного числа величин розміру нуль дорівнює нулю. Критика Зенона була спрямована проти таких представлень, і його чотири парадокси викликали таке хвилювання, що і зараз можна спостерігати деякі брижі. Ці парадокси дійшли до нас завдяки Аристотелю і відомі під назвами Ахіллес, Стріла, Дихотомія (розподіл на два) і Стадіони. Вони сформульовані так, щоб підкреслити протиріччя в поняттях руху і часу, але це зовсім не спроба дозволити такі протиріччя.

Парадокси Ахіллес і Дихотомія, що ми викладемо своїми словами, роз'яснять нам суть цих міркувань.

Ахіллес. Ахіллес і черепаха рухаються в одному напрямку по прямій. Ахіллес куди швидше черепахи, але, щоб її нагнати, йому треба спочатку пройти точку Р, з якої черепаха почала рух. Коли Ахіллес потрапить у Р, черепаха просунеться в точку Р1. Ахіллес не може наздогнати черепаху, поки не потрапить у P1 але черепаха при цьому просунеться в нову точку Р2. Якщо Ахіллес знаходиться в Р2, черепаха виявляється в новій точці Р3 і т.д. Отже, Ахіллес ніколи не може наздогнати черепаху.

Дихотомія. Допустимо, що я хочу пройти від А до В по прямій. Щоб досягти В, мені треба спочатку пройти половину (АВ1) відстані АВ; щоб досягти В2, я повинний спочатку досягти В2 на півдороги від А до В1 і так до нескінченності, так що рух ніколи не зможе початися.

Аргументи Зенона показали, що кінцевий відрізок можна розбити на нескінченне число малих відрізків, кожний з який - кінцевої довжини. Вони показали також, що ми натрапляємо на труднощі при поясненні того, який зміст заяви, що пряма "складається" із крапок. Дуже імовірно, що сам Зенон не мав представлення про те, до яких математичних висновків приводять його міркування. Проблеми, що привели до парадоксів Зенона, незмінно виникають у ході філософських і теологічних дискусій. Ми в них бачимо проблеми, зв'язані з відношенням, потенційної й актуальної нескінченності. Утім, Поль Таннері вважав, що міркування Зенона насамперед були спрямовані проти піфагорійского представлення простору як суми крапок ("крапка є одиниця положення"). Як би справа ні обстояла, безсумнівно, що міркування Зенона впливали на математичну думку багатьох поколінь. Його парадокси можна зіставити з млой, якими користався в 1734 р. єпископ Берклі, показуючи, до яких логічних безглуздостей може привести погане формулювання положень математичного аналізу, але не пропонуючи зі своєї сторони кращого обґрунтування.

Після відкриття ірраціонального розуміння Зенона стали навіть ще більше турбувати математиків. Чи можлива математика як точна наука? Таннері думав, що ми можемо говорити про "дійсний логічний скандал" - про кризу грецької математики. Якщо справа обстояла саме так, то ця криза починається під кінець Пелопонесської війни, що закінчилася падінням Афін (404 р. до н, е.). Тоді ми можемо знайти зв'язок між кризою в математику і кризою суспільної системи, тому що падіння Афін означало смертний вирок пануванню рабовласницької демократії і початок нового періоду верховенства аристократії - криза, що була дозволена вже в дусі нової епохи.

Для цього нового періоду грецької історії характерно те, що росте багатство визначеної частини правлячих класів і так само ростуть убогість і незабезпеченість бідняків. Правлячі класи усе більше засобів для існування одержували за рахунок рабської праці. Це давало їм дозвілля для занять мистецтвом і наукою, але заодно усе більш підсилювало їхню неприхильність до фізичної праці. Ці дозвільні добродії з презирством відносилися до праці рабів і ремісників, і. заспокоєння від турбот вони шукали в заняттях філософією й етикою індивідуума. На таких позиціях коштували Платон і Аристотель. У "Республіці" Платона (написаної, імовірно, близько 360 р. до н.е. ) ми знаходимо саме чітке вираження ідеалів рабовласницької аристократії. "стражі" у республіці Платона повинні вивчати "квадривіум", що складається з арифметики, геометрії, астрономії і музики, для того щоб розуміти закони всесвіту.

Така інтелектуальна атмосфера (принаймні , у своєму ранньому періоді) була сприятлива для обговорення основ математики і для умоглядної космогонії. Частина сторінки з першого видання "Початків" Евкліда, 1482 р.

Щонайменше три великих математики цього періоду були зв'язані з Академією Платона, а саме Архіт, Теєтет (розум. у 369 р.) і Євдокс (ок.408-355). Теєтету приписують ту теорію ірраціональних, котра викладена в десятій книзі "Початків" Евкліда. Ім'я Евдокса зв'язане з теорією відносин, що Евклід дає у своїй п'ятій книзі, а також з так званим методом вичерпування, що дозволив строго проводити обчислення площ і обсягів. Це означає, що саме Євдокс переборов "кризу" у грецькій математиці і що його строгі формулювання допомогли визначити напрямок розвитку грецької аксіоматики і, значною мірою , усієї грецької математики.

Евдоксова теорія відносин покінчила з арифметичною теорією піфагорійців, застосовної тільки до сумірних величин. Це була чисто геометрична теорія, викладена в строгій аксіоматичній формі, і вона зробила зайвими які-небудь застереження щодо чи несумірності сумірності розглянутих величин.

Сучасна теорія ірраціонального числа, побудована Дедекиндом і Вейерштрассом, майже буквально випливає ходу думок Евдокса, але вона відкриває значно більш широкі перспективи завдяки використанню сучасних математичних методів.

"Метод вичерпування" (термін "вичерпування" уперше з'являється в Григорія Сен Венсана, 1647 р.) був відповіддю школи Платона Зенонові. Метод обходив усі пастки нескінченно малого, попросту усуваючи їх, тому що зводив проблеми, у яких могли з'явитися нескінченно малі, до проблем, розв'язуваним засобами формальної логіки. Наприклад, якщо було потрібно довести, що обсяг V тетраедра дорівнює однієї третини обсягу З призми з тією же підставою і тією же висотою, то доказ полягав у тому, щоб показати абсурдність як допущення, що V, так і допущення, що. Для цього була введена аксіома, відома тепер як аксіома Архімеда. Вона лежить в основі теорії відносин Евдокса, а саме: "про ті величини говорять, що вони знаходяться в деякім відношенні одна до іншої, котрі можуть, будучи помножені, перевершити одна іншу" (Евклід V, Визначення 4). Цей метод, що у греків в епоху Відродження став стандартним методом точного доказу при обчисленні площ і обсягів, був цілком строгий, і його легко перетворити на доказ, що відповідає вимогам сучасної математики.

Великим недоліком цього методу було те, що треба було заздалегідь знати результат, щоб його довести, так що математик повинний був спершу прийти до результату менш строгим шляхом, за допомогою проб і спроб.

Є ясні вказівки на те, що такого роду інший метод дійсно використовувався. Ми маємо у своєму розпорядженні лист Архімеда Ератосфену (близько 250 р. до н.е. ), що було виявлено лише в 1906 р. і в який Архімед описує нестрогий, але плідний спосіб одержання результатів. Це лист відомий за назвою "Метод". С. Лур'є висунув припущення, що в ньому виражені погляди математичної школи, що суперничала зі школою Евдокса, виникла, як і та, у період кризи і зв'язана була з Демокрітом, засновником атомістики. Відповідно до теорії Лур'є, школа Демокрита ввела поняття "геометричного атома". Передбачалося, що відрізок прямої, площа, обсяг складаються з великого, але кінцевого числа неподільних "атомів". Обчислення обсягу тіла було підсумовуванням обсягів усіх "атомів", з яких складалося тіло. Ця теорія може показатися безглуздою, якщо не згадати, що деякі математики епохи до Ньютона, особливо Вієт і Кеплер, по суті, користалися такими ж поняттями і вважали окружність складеної з дуже великого числа малюсіньких відрізків. Немає ніяких даних про те, що в стародавності на такій основі був розвитий строгий метод, але наші сучасні поняття межі дали можливість перетворити цю "атомну" теорію в теорію настільки ж строгу, як і метод вичерпування. Навіть у наші дні ми звичайно користуємося таким поняттям "атома" при постановці математичних задач у теорії пружності, чи фізику в хімії, залишаючи строгу теорію з переходами до межі професійним математикам.

Перевага "атомного" методу перед методом вичерпування в тім, що перший полегшує перебування нових результатів. Отже, в античності був вибір між строгим, але відносно марним методом і методом з хибким обґрунтуванням, але більш плідним. Повчально, що майже всі класичні автори застосовують перший метод. Це знов-таки може бути зв'язане з тим, що математика стала коником дозвільного класу, що спирався на рабство, байдужого до винаходів, зі споглядальними інтересами. Можливо і те, що в цьому позначилася перемога в області філософії математики ідеалізму Платона над матеріалізмом Демокріта.

У 334 р. до н.е.. Олександр Македонський почав завоювання Персії. У 323 р., коли він помер у Вавилоні, всей Близьких Схід був у руках греків. Полководці Олександра розділили між собою його завоювання, і згодом виникли три імперії: Єгипет, під владою Птолемеїв; Месопотамія і Сирія, під владою Селевкидів; Македонія, під владою Антигону і його спадкоємців. Навіть у долині Інду були грецькі князі. Почалася епоха еллінізму.

Прямим наслідком походів Олександра було те, що прискорилося проникнення грецької цивілізації у великі райони східного світу. Еллінізувались Єгипет, Месопотамія, частина Індії. Греки заспішили на Близький Схід - торговці, купці, лікарі, мандрівники, найманці, шукачі пригод. У містах - багато хто з них були недавно засновані, що було легко розпізнати по їхніх елліністичних назвах, - військова справа й адміністрація були в руках греків, населення було змішаним, греко-східним. Але еллінізм був істотно міською цивілізацією. Село зберегло своє корінне населення і свій традиційний життєвий уклад. У містах же стара культура Сходу стикалася з імпортованою цивілізацією греків і частково змішалася з нею, хоча завжди залишалося в силі глибоке розходження цих двох світів. Монархи епохи еллінізму користувалися східним звичаям, вирішували східні проблеми керування, але заохочували грецьке мистецтво, грецьку літературу і грецьку науку.

Так і грецька математика була пересаджена в нове середовище. Вона зберегла багато своїх колишніх особливостей, але зазнала впливу від тих адміністративних і астрономічних запитів, що висував Схід. Таке тісне зіткнення грецької науки зі Сходом виявилося винятково плідним, особливо в перші сторіччя. Фактично вся дійсно творча робота, що ми називаємо "грецькою математикою", була пророблена за порівняно короткий термін від 350, до 200 р. до н.е. , від Евдокса до Аполлонія, і навіть досягнення Евдокса відомі нам тільки в тім тлумаченні, у якому ми їх знаходимо в Евкліда й Архімеда. Чудово також, що найбільшого розквіту ця елліністична математика досягла в Єгипті Птолемеєв, а не в Месопотамії, хоча у Вавілоні корінна математика була на більш високому рівні.

Можливо, що це було обумовлено центральним положенням Єгипту тієї епохи в средземноморському світі. Його нова столиця, Олександрія, побудована на березі моря, стала розумовим і господарським центром елліністичного світу. Вавілон же животів, як віддалений центр караванних шляхів, та й зовсім сходив зі сцени - його перемінив Ктесифон-Селевкія, нова столиця імперії Селевкідів. Наскільки відомо, жоден з великих грецьких математиків не був коли-небудь, зв'язаний з Вавілоном. В Антіохії і Пергаме, теж містах Селевкідської імперії, але більш близьких до Середземного моря, були важливі школи грецької науки. Однак корінна вавілонська астрономія і математика саме при Селевкідах досягли свого вищого рівня, і ми тільки тепер починаємо краще розуміти, наскільки істотно був їхній вплив на грецьку астрономію. Афіни стали освітнім центром, а Сіракузи дали Архімеда, найбільшого грецького Математика.

У цю епоху з'явилася професійна вчений-людина, що присвячує своє життя розвитку науки й одержує за це винагороду. Деякі з найбільш видатних представників такої групи людей жили в Олександрії, де Птолемеї побудували великий науковий центр, так званий Музей з його знаменитою бібліотекою. Там зберігалася і множилася наукова і літературна спадщина греків і домоглися при цьому значних успіхів. Одним з перших зв'язаних з Олександрією вчених був Евклід, що є одним з найбільш впливових математиків усіх часів.

Про життя Евкліда ми не маємо ніяких достовірних даних. Ймовірно, він жив у часи першого Птолемея (306-283), якому, відповідно до переказу, він заявив, що до геометрії ні "царської дороги". Його найбільш знаменитий і найбільш видатний здобуток - тринадцять книг його "Початки" (Stoіcheіa), але йому приписують кілька інших менших праць. Серед останніх так звані "Дані" (Data), що містять те, що ми назвали б додатками алгебри до геометрії, але все це викладено строго геометричною мовою. Ми не знаємо, яка частина цих праць належить самому Евкліду і якій частині складають компіляції, але в багатьох місцях виявляється разюча проникливість. Це перші, математичні праці, що дійшли до нас від древніх греків цілком. В історії Західного світу "Початки", після Біблії, ймовірно, найбільше число раз видана і найбільше вивчаєма книга. Після винаходу друкарства з'явилося більше тисячі видань, а до того ця книга, переважно в рукописному виді, була основною при вивченні геометрії. Велика частина нашої шкільної геометрії запозичена часто буквально з перших шести книг "Початки", і традиція Евкліда дотепер тяжіє над нашим елементарним навчанням. Для професійного математика ці книги усе ще мають непереборне зачарування, а їхня логічна побудова вплинула на наукове мислення, мабуть, більше, аніж який би то не був інший здобуток. Виклад Евкліда побудований у виді строго логічних висновків теорем із системи визначень, постулатів і аксіом. У перших чотирьох книгах розглядається геометрія на площині. Виходячи з найбільш простих властивостей ліній і кутів, ми приходимо тут до рівності трикутників, рівності площ, теоремі Піфагора, побудові квадрата, рівновеликого заданому прямокутнику, до золотого перетину, кола і до правильних багатокутників. У книзі V викладена Євдоксова теорія непорівнянних у її чисто геометричній формі, у книзі VІ ця теорія застосована до подоби трикутників. Таке введення подоби - на настільки пізньому етапі - складає одне з найбільш істотних розходжень між викладом планометрії в Евкліда і сучасним. Ці геометричні розгляди завершуються в десятій книзі, де багато хто вважає найбільш важкої в Евкліда. У ній дана геометрична класифікація квадратичних ірраціональностей і коренів квадратних з них, тобто тих чисел, що ми представляємо у виді . В останніх трьох книгах викладається геометрія в просторі. Від тілесних кутів, обсягів паралелепіпедів, призм і пірамід ми доходимо тут до кулі і до того, що за задумом повинне, видимо, вінчати всю працю: дослідження п'яти правильних ("Платонових") тіл і доказу, що їх існує тільки п'ять.

Книги VІІ -ІX присвячені теорії чисел, але не техніці обчислень, а таким "піфагорейским" питанням, як подільність цілих чисел, підсумовування геометричних прогресій, і деяким властивостям простих чисел. Отут ми зустрічаємо і "алгоритм Евкліда" для визначення найбільшого загального дільника заданої системи чисел, і "теорему Евкліда", що простих чисел нескінченно багато. Особливий інтерес представляє теорема VІ, у ній мова йде про першу з задач, що дійшли до нас, на максимум і доводиться, що з прямокутників заданого периметра найбільшу площу має квадрат. П'ятий постулат книги І (неясно, у якім відношенні знаходяться в Евкліда "аксіоми" і "постулати") еквівалентний так називаній "аксіомі рівнобіжних", відповідно до якої через крапку поза заданою прямою можна провести одну і тільки одну пряму, їй рівнобіжну. Спроби зробити з цієї аксіоми теорему змусили в дев'ятнадцятому сторіччі цілком оцінити мудрість Евкліда: це твердження було визнано аксіомою й у зв'язку з цим минулого відкриті інші, так називані неевклідової геометрії.

Алгебраїчні висновки в Евкліда приводяться винятково в геометричному виді. Вираження виду вводиться як сторона квадрата з площею А, добуток а*в - це площа прямокутника зі сторонами а і в. Такий спосіб представлення насамперед був викликаний теорією відносин Евдокса, у якій свідомо відкидалися чисельні вираження для відрізків прямої і, таким чином, непорівнянні розглядалися тільки геометрично: "числами" вважалися тільки цілі чи числа раціональні дроби.

Яку мету ставив собі Евклід, коли писав свої "Початки"? Ми можемо з відомою впевненістю думати, що він хотів спільно викласти в одній праці три великих відкриття недавнього минулого: теорію відносин Евдокса, теорію ірраціональних Теєтета і теорію п'яти правильних тіл, що займали видатне місце в космології Платона. То були три типово "грецьких" досягнення.

Найбільшим математиком епохи еллінізму й усього древнього світу був Архімед (287-212), що жив у Сіракузах, де він був радником Гієрона. Він - один з деяких вчених античності, яких ми знаємо не тільки по імені: збереглися деякі зведення про його життя й особистість. Ми знаємо, що він був убитий, коли римляни взяли Сіракузи, при облозі яких технічне мистецтво Архімеда було використано захисниками міста. Подібна схильність до практичних застосувань представляється нам дуже незвичайною, якщо врахувати, з яким презирством до цього відносилися сучасники Архімеда зі школи Платона. Однак пояснення нам дає багато разів цитоване повідомлення Плутарха (у життєписі Марцеяла), а саме: "Хоча ці винаходи заслужили йому репутацію надлюдської проникливості, він не дойшов до того, щоб залишити який-небудь писаний твір з таких питань, а, вважаючи низькою і невартою справою механіку і мистецтво будь-якого роду, якщо воно має на меті користь і вигоду, усі свої честолюбні домагання він засновував на власних поглядах", краса і тонкість яких не заплямовані якою-небудь домішкою звичайних життєвих нестатків".

Найбільш важливий внесок Архімеда в математику відноситься до тієї області, що тепер ми називаємо інтегральним численням: теореми про площі плоских фігур і про обсяги тел. У "Вимірі кола" він знайшов наближене вираження для окружності, користаючись уписаними й описаними правильними багатокутниками. Дійшовши в цьому наближенні до багатокутників з 96 сторонами, він знайшов (у наших позначеннях), що

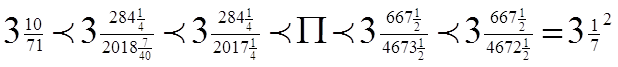
Звичайно про це повідомляють, говорячи, що П приблизно дорівнює 3. У книзі Архімеда "Про сферу і циліндр" ми знаходимо вираження для поверхні сфери (у такому виді: поверхня сфери в чотири рази більше площі великого кругу) і для обсягу сфери (у такому виді: обсяг сфери дорівнює обсягу описаного циліндра).

У книзі про "Спіралі" ми знаходимо "спіраль Архімеда" і обчислення площ, а в книзі "Про коноїди і сфероїди" - обсяги деяких тіл, утворених обертанням кривих другого порядку.

Ім'я Архімеда зв'язано також з його теоремою про утрату ваги тілами, зануреними в рідину. Ця теорема знаходиться в трактаті по гідростатиці "Про тіла, що плавають,".

В усіх цих працях Архімеда разюча оригінальність думки сполучається з майстерною технікою обчислень і зі строгістю доказів. Характерні для цієї строгості вже згадана "аксіома Архімеда" і постійне використання методу вичерпування при доказі його інтеграційних результатів. Ми бачили, що фактично він знаходив ці результати більш евристичним шляхом ("зважуючи" нескінченно малі), але потім він публікував їх, дотримуючи самі тверді вимоги строгості.

Достаток обчислень в Архімеда відрізняє його від більшості творчих математиків Греції. Це додає його працям, при всіх їхній типово грецьких особливостях, східний відтінок. Такий відбиток помітний у його "Задачі про бики" - дуже складній задачі невизначеного аналізу, яку можна витлумачити як задачу, що приводить до рівняння

t2 – 4729494u2=1

типи "рівняння Пелля", що зважується в дуже великих (цілих) числах. Це лише одне з багатьох вказівок на те, що традиції Платона ніколи безроздільно не гocподарювали в математиці еллінізму, і на те ж саме вказує елліністична астрономія.

9. З третім великим математиком еллінізму, Аполлонієм з Перги (260-170), ми знову цілком у руслі геометричної традиції греків. Аполлоній, що, очевидно, вів навчання в Олександрії й у Пергамі, написав трактат з восьми книг про конічні перетини ("Про коніків"). Сім книг збереглося, три з них - тільки в арабському перекладі. Це - трактат про еліпс, параболу і гіперболу, обумовлених як перетину кругового конуса, де виклад доведений до дослідження эволют конічного перетину. Ми називаємо ці криві, випливаючи Аполлонію; ці назви виражають одне з властивостей цих кривих, зв'язане з площами і що виражається, у наших позначеннях, рівняннями

у2 = рх, у2 = рх ± х2

"(запис однорідна, в Аполлонія р и d - відрізки; знак " + " дає гіперболу, знак "-" дає еліпс). Парабола тут значить "додаток", еліпс - "додаток з недоліком", гіпербола - "додаток з надлишком". Аполлоній не розташовував нашим координатним методом, тому що він не мав у своєму розпорядженні алгебраїчні позначення (ймовірно, він свідомо, під впливом школи Євдокса, відкидав їх). Однак його результати можна відразу записати мовою координат, включаючи властивість, що збігається з тим, що виражається їхнім рівнянням у декартових координатах. Те ж саме можна сказати про інші книги Аполлонія, що збереглися частково. Вони містять "алгебраїчну"