Двокроковий метод найменших квадратів
Двокроковий метод найменших квадратів
Нехай маємо таку модель:
функція доходу:
![]() (1)
(1)
функція пропозиції грошей:
![]() (2)
(2)
де ![]() – доход;
– доход; ![]() – запас грошей;
– запас грошей; ![]() – інвестиційні витрати;
– інвестиційні витрати; ![]() – витрати уряду на товари та послуги.
– витрати уряду на товари та послуги.
Змінні ![]() та
та ![]() є екзогенними,
є екзогенними, ![]() та
та ![]() – ендогенними.
– ендогенними.
Рівняння доходу, яке ми розглядаємо, показує, що доход визначається пропозицією грошей, інвестиційними витратами та витратами уряду. Рівняння пропозиції грошей показує, що запас грошей визначається відповідно до рівня доходів. Очевидно, що ми маємо симультативну модель.
Застосовуючи умову порядку для її ототожнення, бачимо, що рівняння доходу неототожнене, тоді як рівняння пропозиції грошей – переототожнене. Переототожнена функція пропозиції грошей не може бути оцінена за допомогою методу ННК, тому що ми отримаємо дві різні оцінки ![]() .
.
Якщо застосувати метод найменших квадратів для оцінки невідомих параметрів рівняння пропозиції грошей, то отримані оцінки будуть зміщеними через кореляцію між змінною ![]() та випадковою величиною
та випадковою величиною ![]() . Припустимо, що ми знайшли змінну, близьку до змінної
. Припустимо, що ми знайшли змінну, близьку до змінної ![]() в тому сенсі, що вона високо корелює з
в тому сенсі, що вона високо корелює з ![]() , але не є корельованою з
, але не є корельованою з ![]() . Така змінна називається допоміжною змінною. Якщо її можна знайти, то МНК можна застосовувати для оцінки функції грошової пропозиції. Але як отримати таку допоміжну змінну? За допомогою методу двокрокових найменших квадратів. З назви видно, що метод складається з двох етапів.
. Така змінна називається допоміжною змінною. Якщо її можна знайти, то МНК можна застосовувати для оцінки функції грошової пропозиції. Але як отримати таку допоміжну змінну? За допомогою методу двокрокових найменших квадратів. З назви видно, що метод складається з двох етапів.
1. Щоб позбавитись кореляції між ![]() і
і ![]() , побудуємо спочатку регресійне рівняння залежності
, побудуємо спочатку регресійне рівняння залежності ![]() від усіх попередньо визначених змінних:
від усіх попередньо визначених змінних:
![]() (3)
(3)
де et є помилками. Невідомі параметри рівняння (3) отримаємо за допомогою МНК:
![]() (4)
(4)
Рівняння (3) є нічим іншим, як регресією скороченої форми, тому що в правій частині з'являються тільки екзогенні або попередньо визначені змінні. Його ще можна записати у вигляді:
![]() (5)
(5)
який показує, що змінна ![]() складається з двох частин:
складається з двох частин: ![]() – прогнозної величини та випадкової компоненти еt. Виходячи з класичних припущень методу найменших квадратів,
– прогнозної величини та випадкової компоненти еt. Виходячи з класичних припущень методу найменших квадратів, ![]() та et – некорельовані між собою.
та et – некорельовані між собою.
2. Рівняння пропозиції грошей можна записати таким чином:
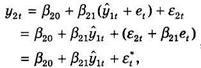 (6)
(6)
де ![]() .
.
Порівнюючи (6) з (2) бачимо, що зовні ці рівняння дуже схожі, єдина відмінність полягає в тому, що ![]() замінено на
замінено на ![]() . В чому полягає перевага рівняння у вигляді (6)? Хоча
. В чому полягає перевага рівняння у вигляді (6)? Хоча ![]() в початковому рівнянні грошової пропозиції корелює з відхиленням
в початковому рівнянні грошової пропозиції корелює з відхиленням ![]() ,
, ![]() в (6) не корелюється з
в (6) не корелюється з ![]() (у випадку, коли розмір моделі зростає пропорційно). В результаті, МНК можна застосувати до (6), з якого можна знайти відповідні оцінки параметрів функції пропозиції грошей.
(у випадку, коли розмір моделі зростає пропорційно). В результаті, МНК можна застосувати до (6), з якого можна знайти відповідні оцінки параметрів функції пропозиції грошей.
Для подальшої ілюстрації методу 2МНК видозмінимо модель доходу та пропозиції грошей:
![]() (7)
(7)
![]() (8)
(8)
де додатково ![]() – доход у попередньому періоді;
– доход у попередньому періоді; ![]() – пропозиція грошей у попередньому періоді (вважаємо, що
– пропозиція грошей у попередньому періоді (вважаємо, що ![]() та
та ![]() – попередньо визначені). Обидва рівняння (7) і (8) є переототожненими. Для того, щоб застосувати метод 2МНК, на першому етапі побудуємо регресійну модель залежності ендогенних змінних від усіх попередньо визначених змінних:
– попередньо визначені). Обидва рівняння (7) і (8) є переототожненими. Для того, щоб застосувати метод 2МНК, на першому етапі побудуємо регресійну модель залежності ендогенних змінних від усіх попередньо визначених змінних:
![]() (9),
(9), ![]() (10)
(10)
На другому етапі заміщуємо ![]() та
та ![]() в початкових (структурних) рівняннях їхніми оціненими значеннями з двох попередніх регресій:
в початкових (структурних) рівняннях їхніми оціненими значеннями з двох попередніх регресій:
![]() (11)
(11)
![]() (12)
(12)
де![]()
Отримані таким чином оцінки будуть спроможними, тобто з розміром вибірки наближатимуться до BLUE-оцінок.
Можна виділити такі особливості методу 2МНК.
1. Метод можна застосувати до окремого рівняння в системі без врахування інших. Отже, для економетричних моделей, що складаються з великої кількості рівнянь, метод 2МНК є дуже економним, тому він широко використовується на практиці.
2. На відміну від МНК, який дає декілька різних оцінок параметра у переототожнених рівняннях, 2МНК дає лише одну оцінку параметра.
3. Для застосування методу потрібно знати тільки загальну кількість екзогенних або попередньо визначених змінних у системі.
4. Хоча метод 2МНК був спеціально розроблений для переототожнених рівнянь, його також можна застосовувати до точно ототожнених рівнянь. У цьому разі МНК та 2МНК дадуть ідентичні оцінки.
Задача № 1
У таблиці наведені статистичні дані для економічного показника ![]() та фактора
та фактора ![]() :
:
Рік |
|
|
| 1987 | 30 | 18 |
| 1988 | 33 | 19 |
| 1989 | 38 | 21 |
| 1990 | 47 | 22 |
| 1991 | 54 | 24 |
Подобные работы: