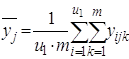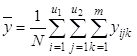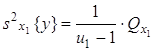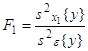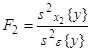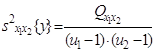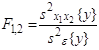Дисперсионный анализ при помощи системы MINITAB для WINDOWS
Министерство образования и науки Украины
Севастопольский национальный технический
университет

МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению лабораторной работы № 3 и 4
” Дисперсионный анализ при помощи системы
MINITAB для WINDOWS “
по учебной дисциплине “Прикладная статистика”
для студентов экономических специальностей
всех форм обучения
Севастополь
2008
Методические указания рассмотрены и утверждены на заседании кафедры менеджмента и экономико -математических методов протокол № “_____” от “______________” 2008г.
Рецензент: доцент департамента учета и аудита Т.А.Мараховская
1. Цель работы
Изучение возможностей дисперсионного анализа, для выявления зависимостей между экономическими показателями и получение практических навыков работы в системе MINITAB.
Теоретические сведения
2.1. Дисперсионный анализ
2.1.1. Однофакторный дисперсионный анализ
При проведении экономического анализа часто необходимо оценить влияние на целевую функцию y качественного фактора x . Таким фактором могут быть, например, партии сырья, отрасли промышленности, регионы и т.д.
Пусть данные о влиянии некоторого качественного фактора на количественный в форме таблицы.
Таблица 1.1. – влияние качественного фактора на исследуемый показатель
|
| … |
|
|
| …. |
|
|
| … |
|
| … | … | … | … |
|
|
|
Модель зависимости значений ![]() от фактора столбцов можно представить в следующем виде (1-4):
от фактора столбцов можно представить в следующем виде (1-4):
![]()
где ![]() - общее среднее,
- общее среднее, ![]() -отклонение от общего среднего для j-го уровня фактора,
-отклонение от общего среднего для j-го уровня фактора, ![]() - случайная составляющая.
- случайная составляющая.
По выборочным данным можно вычислить:
1) среднее ![]() для каждого уровня фактора (среднее по столбцам)xj (j=1,2,...u ), по mj параллельным опытам, где mj– число данных в столбце j:
для каждого уровня фактора (среднее по столбцам)xj (j=1,2,...u ), по mj параллельным опытам, где mj– число данных в столбце j:
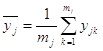 ;
;
2) общее среднее ![]() по всем N опытам, т.е. по всем mj параллельным опытам на всех уровнях фактора xj (
по всем N опытам, т.е. по всем mj параллельным опытам на всех уровнях фактора xj (![]() ):
):
![]() ;
;
3) общую сумму квадратов отклонений Q0:
![]()
4) сумму квадратов, характеризующую влияние фактора x (отклонения между группами)
![]() ;
;
5) остаточную сумму квадратов, зависящую от ошибки e (отклонения внутри групп)
![]() .
.
Тождество дисперсионного анализа имеет вид:
![]()
На основании вычисленных сумм квадратов вычисляются:
1) оценка дисперсии относительно общего среднего![]() :
:
![]() ,
,
где ![]() - число степеней свободы;
- число степеней свободы;
2) оценка дисперсии «между группами», определяемыми уровнями xj:
![]()
где число степеней свободы ![]() .
.
3) выборочная оценка дисперсии «внутри групп», вычисляемая как средняя оценка по всем u группам:
![]()
с числом степеней свободы ![]()
Числа степеней свободы должны удовлетворять соотношению
![]()
Для того, чтобы сделать вывод о том, влияет ли на исследуемые показатели качественный фактор, сопоставляют дисперсию между группами с общей дисперсией. При этом выдвигают следующие гипотезы:
H0: ![]() , т.е средние значения по всем столбцам равны и равны общему среднему, откуда следует, что среднеквадратическое отклонение по факторам равно среднеквадратическому отклонению по всем данным и равно нулю. Т.е. качественный фактор не оказывает влияния на исследуемый показатель.
, т.е средние значения по всем столбцам равны и равны общему среднему, откуда следует, что среднеквадратическое отклонение по факторам равно среднеквадратическому отклонению по всем данным и равно нулю. Т.е. качественный фактор не оказывает влияния на исследуемый показатель.
H1: ![]() , , т.е средние значения по всем столбцам не равны между собой и не равны общему среднему, откуда следует, что среднеквадратическое отклонение по факторам не совпадает со среднеквадратическим отклонением по всем данным. Т.е. качественный фактор оказывает существенное влияние на исследуемый показатель.
, , т.е средние значения по всем столбцам не равны между собой и не равны общему среднему, откуда следует, что среднеквадратическое отклонение по факторам не совпадает со среднеквадратическим отклонением по всем данным. Т.е. качественный фактор оказывает существенное влияние на исследуемый показатель.
Оценивание значимости влияния фактора x выполняется по F-критерию Фишера, для чего формируется следующее F-отношение:
![]() .
.
Фактор x признается незначимым, если соответствующее F-отношение оказывается меньше критического, выбранного из таблиц для принятого уровня значимости ![]() и числа степеней свободы сравниваемых дисперсий
и числа степеней свободы сравниваемых дисперсий ![]() и
и ![]() .
.
Табличное значение критерия Фишера определяется дл числа степеней свободы u-1 и N-1 и вероятности ошибки ![]() .
.
Т.е если ![]() , то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.
, то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.
Если ![]() , то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.
, то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.
Результаты дисперсионного анализа сводятся в таблицу 2.
Таблица 2 Однофакторный дисперсионный анализ
Источник изменчивости | Сумма квадратов отклонений | Число степеней свободы | Оценка дисперсии | F – отношение |
| Между группами |
|
|
|
|
Внутри групп ( ошибка e) |
|
|
| |
| Общая сумма |
|
|
|
![]() - число данных в столбце, u- число столбцов, m – число строк.
- число данных в столбце, u- число столбцов, m – число строк.
2.1.2. Двухфакторный дисперсионный анализ при перекрестной
классификации факторов
Часто необходимо качественно оценить значимость или незначимость влияния на целевую функцию u двух одновременно действующих факторов x1 и x2 . Такими факторами могут быть, например, форма собственности предприятия x1 ивид экономической деятельности x2.
Модель двухфакторного дисперсионного анализа имеет вид (1-4):
![]()
где ![]() - общее среднее,
- общее среднее, ![]() -отклонение от общего среднего для фактора x1,
-отклонение от общего среднего для фактора x1, ![]() - отклонение от общего среднего для фактора x2,
- отклонение от общего среднего для фактора x2, ![]() - отклонение от общего среднего для взаимодействия двух факторов,
- отклонение от общего среднего для взаимодействия двух факторов, ![]() - случайная составляющая.
- случайная составляющая.
В этом случае общую сумму квадратов отклонений Q0 можно разбить на четыре суммы:
1) Qx1-по фактору x1,
2) Qx2-по фактору x2,
3) Qe-остаточную сумму квадратов, зависящую от ошибки e,
4) Q x1x2-зависящую от взаимодействия (произведения) x1x2 двух факторов.
В этом случае по выборочным значениям вычисляются:
1) среднее ![]() для каждого уровня фактораx1:
для каждого уровня фактораx1:
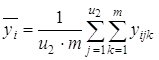 ;
;
2) среднее ![]() для каждого уровня фактора x2:
для каждого уровня фактора x2:
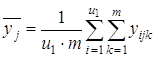 ;
;
3) общее среднее ![]() по всем N опытам, т.е. по всем m параллельным опытам на всех сочетаниях уровней факторов x1 и x2 (
по всем N опытам, т.е. по всем m параллельным опытам на всех сочетаниях уровней факторов x1 и x2 (![]() ):
):
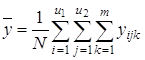 ;
;
4) среднее ![]() по m параллельным опытам для каждого сочетания уровней факторов x1 и x2:
по m параллельным опытам для каждого сочетания уровней факторов x1 и x2:
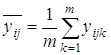 .
.
В табл.2 показаны данные полного факторного эксперимента с одинаковым числом наблюдений в ячейках.
Таблица 3. - Данные эксперимента и расчёты средних при двухфакторном дисперсионном анализе
| j = | 1 | 2 | … |
|
| |
| k |
|
| … |
| |
| 1 | 1 |
| ||||
| 2 |
| |||||
| … | … | |||||
| m |
| |||||
. . . | 1 | |||||
| 2 | ||||||
| … | ||||||
| m | ||||||
| 1 | |||||
| 2 | ||||||
| … | ||||||
| m | ||||||
|
| |||||
В табл.2 ![]()
![]() вычисляется по выделенной части столбца, содержащей m параллельных опытов.
вычисляется по выделенной части столбца, содержащей m параллельных опытов.
Общая сумма квадратов отклонений Q0 рассчитывается по формуле:
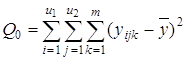
Эту сумму можно разложить на 4 составляющие:
1) сумму, характеризующую влияние фактора x1:
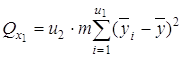 ;
;
2) сумму, характеризующую влияние фактора x2:
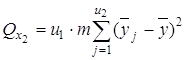 ;
;
3) сумму, характеризующую результат влияния взаимодействия x1x2:
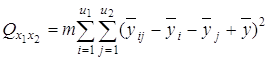
4) сумму, характеризующую влияние ошибки e:
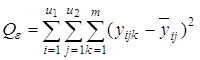
Указанные пять сумм, поделенные на соответствующее число степеней свободы, дают пять различных оценок дисперсии, если влияние факторов x1 и x2 незначимо. Для проведения дисперсионного анализа вычисляются следующие дисперсии:
1) оценка дисперсии относительно общего среднего![]() :
:
![]() ,
,
где ![]() -общее число наблюдений, а число степеней свободы
-общее число наблюдений, а число степеней свободы
![]() ;
;
2) оценка дисперсии «между строками», определяемыми уровнями x1j:
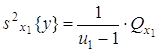 ,
,
где ![]() - число степеней свободы.
- число степеней свободы.
3) оценка дисперсии «между столбцами», соответствующими уровням фактора x2:
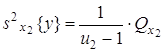 ,
,
где ![]() - число степеней свободы;
- число степеней свободы;
4) оценка дисперсии «между сериями» по m параллельным опытам каждая
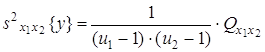
с числом степеней свободы ![]() ;
;
5) оценка дисперсии «внутри серий» по m параллельным опытам, вычисляемая как средняя оценка по всем u1u2 сериям:
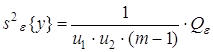
с числом степеней свободы ![]() .
.
Числа степеней свободы должны удовлетворять соотношению
![]()
Статистическое оценивание значимости влияния факторов x1 , x2 и взаимодействия x1x2 выполняются по F-критерию Фишера, для чего формируются следующие F-отношения:
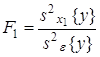 ,
, 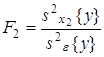 ,
, 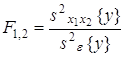 .
.
Фактор x1 или x2 , или взаимодействие x1x2 признаются незначимым, если соответствующее F-отношение оказывается меньше критического, выбранного из таблиц для принятого уровня значимости ![]() и числа степеней свободы сравниваемых дисперсий.
и числа степеней свободы сравниваемых дисперсий.
Для того, чтобы сделать вывод о том, влияют ли на исследуемые показатели качественные факторы, выдвигают следующие гипотезы:
H0: ![]() , т.е средние значения по всем столбцам равны фактор столбца не оказывает влияния на исследуемый показатель.
, т.е средние значения по всем столбцам равны фактор столбца не оказывает влияния на исследуемый показатель.
H1: ![]() , , т.е средние значения по всем столбцам не равны фактор столбца оказывает существенное влияние на исследуемый показатель.
, , т.е средние значения по всем столбцам не равны фактор столбца оказывает существенное влияние на исследуемый показатель.
H0: ![]() , т.е средние значения по всем строкам равны фактор строки не оказывает влияния на исследуемый показатель.
, т.е средние значения по всем строкам равны фактор строки не оказывает влияния на исследуемый показатель.
H1: ![]() , , т.е средние значения по всем строкам не равны фактор строки оказывает существенное влияние на исследуемый показатель.
, , т.е средние значения по всем строкам не равны фактор строки оказывает существенное влияние на исследуемый показатель.
H0: ![]() , т.е отклонение взаимодействия факторов равно нулю и взаимодействие не значимо..
, т.е отклонение взаимодействия факторов равно нулю и взаимодействие не значимо..
H1: ![]() , фактор взаимодействия значим..
, фактор взаимодействия значим..
Если ![]() , то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.
, то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.
Если ![]() , то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.
, то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.
Результаты двухфакторного дисперсионного анализа представляются в виде табл.3.
Таблица 3. - Двухфакторный дисперсионный анализ при равном числе наблюдений в ячейках
| Вид изменчивости | Сумма квадратов отклонений | Число степеней свободы | Оценка дисперсии | F – отношение |
От фактора x1 |
|
|
|
|
От фактора x2 |
|
|
|
|
От взаимо-действия x1x2 |
|
|
|
|
Остаточная (от e) |
|
|
| |
| Общая |
|
|
|
m – число данных в строке (число повторов в ячейке), ![]() - число столбцов,
- число столбцов, ![]() - число строк.
- число строк.
3. Дисперсионный анализ в системе MINITAB
Для проведения дисперсионного анализа в системе MINITAB необходимо выбрать из меню Stat > ANOVA.
Различные возможности проведения дисперсионного анализа представлены следующими командами.
Команда Oneway позволяет провести однофакторный дисперсионный анализ, если значения выходного и влияющего параметра записаны в двух столбцах.
Команда Oneway(Unstacked) позволяет провести однофакторный дисперсионный анализ, если значения выходного параметра разбито на группы и значения для каждой группы записаны в разных столбцах.
Команда Twoway позволяет провести двухфакторный анализ для сбалансированных данных (с одинаковым количеством значений в каждой ячейке).
Команда Balanced ANOVA позволяет провести многофакторный дисперсионный анализ для сбалансированных моделей с перекрестной и иерархической классификацией.
Команда General Linear Model позволяет провести многофакторный несбалансированный дисперсионный анализ для моделей с перекрестной и иерархической классификацией.
3.2.1. Однофакторный дисперсионный анализ
Для проведения однофакторного дисперсионного анализа необходимо подготовить данные в двух столбцах (в первом – входная переменная, качественная, во втором – выходная переменная), выбрать из меню Stat > ANOVA > Oneway и заполнить открывшееся диалоговое окно.
Диалоговое окно.
1. Отклик (Response) – выберите столбец, содержащий выходную (зависимую) переменную. Столбец должен содержать только числовые значения.
2. Фактор (Factor) – выберите столбец, содержащий качественную переменную, влияние которой исследуется. Фактор может иметь как числовые, так и символьные значения.
3. Сохранить остатки (Store Residuals), выбирается, если необходимо сохранить остатки для последующего анализа. Остатки сохраняются в свободном столбце.
4. Сохранить оценки (Store fits) Для однофакторного анализа оценки это средние значения для каждого уровня фактора.
5. Графики
Пример 1
Пусть данные о проценте износа оборудования для 12 предприятий разных отраслей промышленности и форм собственности представлены следующей таблицей.
Таблица 4.
Исходные данные
| Field | Owner | d |
| Пищевая | Частн | 31 |
| Пищевая | Частн | 49 |
| Пищевая | Частн | 37 |
| Пищевая | Госуд | 47 |
| Пищевая | Госуд | 57 |
| Пищевая | Госуд | 53 |
| Машиностр | Госуд | 43 |
| Машиностр | Госуд | 59 |
| Машиностр | Госуд | 56 |
| Машиностр | Частн | 47 |
| Машиностр | Частн | 51 |
| Машиностр | Частн | 53 |
Подобные работы:
Доверительные интервалы прогноза. Оценка адекватности и точности моделей
Економіко-математичне моделювання в управлінні підприємством аграрно-промислового комплексу
Економіко-математичне моделювання діяльності кредитних спілок
Економіко-математичне моделювання процесу ціноутворення на ринку опціонів
Економіко-математичне моделювання та прогноз характеристик цінних паперів
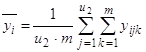
 i =
i =