Алгоритмы с многочленами

1. Многочлены

2. Деление многочленов

2.1. Делимость многочленов. Свойства делимости

2.2. Деление многочленов с остатком

2.3. Наибольший общий делитель многочленов

2.4. Алгоритм Евклида

3. Кратные корни

4. Производная от многочлена

5. Кратные множители

5.1. Выделение кратных множителей

Заключение

Список использованной литературы

Введение

Тема моей дипломной работы: «Алгоритмы с многочленами».

Целью данной работы является изучение многочленов, алгоритмов с ними, рассмотрение возможностей составления различных программ. Для достижения поставленной цели необходимо рассмотреть следующие вопросы:

– делимость многочленов;

– деление многочленов с остатком;

– наибольший общий делитель, алгоритм Евклида;

– кратные корни;

– кратные множители, выделение кратных множителей;

– производные от многочленов.

Для выполнения дипломной работы я поставила следующие задачи:

1. изучить литературу о многочленах;

2. применить теорию высшей алгебры в решении задач элементарной математики;

3. составить программы для нахождения частного и остатка при делении многочленов, наибольшего общего делителя двух многочленов, производной многочлена; разложения многочленов на кратные множители.

Общий вид уравнения n-ной степени (где n некоторое положительное число) есть

. (1.1)

Коэффициенты этого уравнения мы будем считать произвольными комплексными числами, причем старший коэффициент должен быть отличным от нуля.

Если написано уравнение (1.1), то всегда предполагается, что требуется его решить, найти такие числовые значения для неизвестного x, которые удовлетворяют этому уравнению, то есть после подстановки вместо неизвестного и выполнения всех указанных операций обращают левую часть уравнения (1.1) в нуль.

Целесообразно заменить задачу решения уравнения (1.1) более общей задачей изучения левой части этого уравнения

, (1.2)

называемой многочленом -ной степени от неизвестного х. Многочленом называется лишь выражение вида (1.2), то есть лишь сумма целых неотрицательных степеней неизвестного x, взятых с некоторыми числовыми коэффициентами. В частности, мы не будем считать многочленами такие выражения, которые содержат неизвестное x с отрицательными или дробными показателями. Для сокращенной записи многочленов употребляются символы f(x), g(x) и так далее.

Теория многочленов в определенном отношении похожа на теорию целых чисел, хотя внешне эти две теории не имеют ничего общего. Внутренняя же близость, схожесть этих теорий объясняется тем, что для многочленов, так же как и для целых чисел, можно определить деление и, что еще более важно, деление с остатком.

2.1. Делимость многочленов. Свойства делимости

Многочлен делится на многочлен , если существует такой многочлен , что выполняется равенство

(2.1)

Например, из равенства следует, что делится на многочлен и на многочлен .

Многочлен в равенстве (2.1) определяется однозначно. Если бы существовал многочлен , удовлетворяющий равенству (2.1), то мы получили бы, что

(2.2)

откуда

Но многочлен по условию ненулевой, и в силу утверждения или нулевом является многочлен , т.е. многочлен совпадает с .

Многочлен в равенстве (2.1) называется частным от деления на , а – делителем.

Укажем некоторые основные свойства делимости многочленов.

1. Если делится , а делится на , то будет делиться на .

В самом деле, по условию и , а поэтому .

2. Если и делятся на , то их сумма и разность также делятся на .

Из равенств и вытекает .

3.Если делится на , то произведение на любой многочлен также будет делиться на .

Если , то .

Из 2. и 3. вытекает следующее свойство:

4. Если каждый из многочленов делится на , то на будет делиться и многочлен , где - произвольные многочлены.

5. Всякий многочлен делится на любой многочлен нулевой степени.

Если , а с - произвольное число, не равное нулю, то есть произвольный многочлен нулевой степени, то .

6. Если делится на , то делится и на с, где с – произвольное число отличное от нуля.

Из равенства следует равенство .

7. Многочлены , , и только они будут делителями многочлена , имеющими такую же степень, что и .

Действительно, . То есть делится на .

Если делится на , причем степени и совпадают, то степень частного от деления на должна быть равной нулю, то есть , , откуда .

Отсюда вытекает следующее свойство:

8. Тогда и только тогда многочлены , одновременно делятся друг на друга, если , .

Из 1. и 8. вытекает свойство:

9. Всякий делитель одного из двух многочленов , , где , будет делителем и для другого многочлена.

Свойства делимости многочленов могут быть применены для изучения делимости в множестве целых чисел. Выясним, например, для каких целых чисел числоявляется простым.

Натуральное число, отличное от 1, называется простым, если оно делится только на 1 и на само себя; целое отрицательное число k называется простым, если число –k простое.

Для ответа на поставленный вопрос заметим, что справедливо равенство

(2.3)

и поэтому число делится на и на Следовательно, оно может быть простым только в случае, когда один из этих делителей равен 1 или –1, т.е. выполняется хотя бы одно из равенств

Остается проверить следующие значения : 3, 1, 0, -3, -1 и –2. При этих значениях рассматриваемое число равно соответственно 19, -5, 3, 4, так что искомое множество чисел есть

Может возникнуть вопрос: откуда взялось равенство (2.3)? Как мы догадались, что многочлен таким образом раскладывается на множители? Для нахождения разложений такого типа необязательно прибегать к искусственным группировкам, это можно сделать с помощью теории, которая будет изложена ниже.

Из этого примера видно, что уже для решения задач, связанных с делимостью целых чисел, полезно уметь выяснять, делится ли данный многочлен на некоторый другой многочлен (раскладывается ли на множители).Ответ на такой и многие другие вопросы можно найти с помощью деления многочлена с остатком.

2.2. Деление многочленов с остатком

Для многочленов, как и для целых чисел, существует алгоритм деления с остатком.

Теорема о делении с остатком. Для любых двух многочленов f(x) и g(x) можно найти такие многочлены q(x) и r(x , что

f(x)=g(x)q(x)+r(x),

причем степень r(x) меньше степени g(x) или же r(x)=0. Многочлены q(x) и r(x), удовлетворяющие этому условию, определяются однозначно.

Если разности f(x)-r(x) и обе делятся наg(x), то их разностьтакже делится наg(x). Если бы многочлен (x) был ненулевым, то он имел бы степень меньшую, чем g(x), и не мог бы тогда делится наg(x). Следовательно, (x)=0, так что .

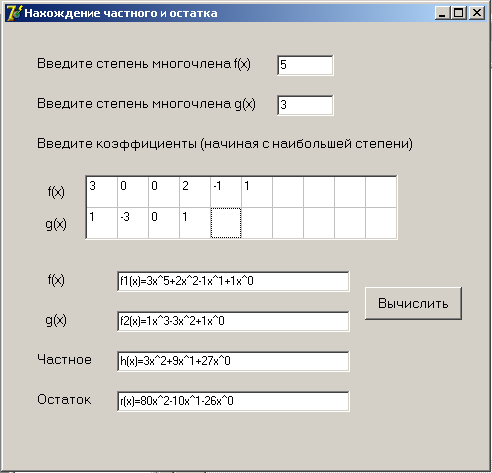
В практической деятельности для нахождения частного и остатка применяют способ вычисления, называемый «деление углом». Покажем его на примере.

Пример. Найти частный и остаток от деления на .

1. и

|

Частным от деления на является многочлен , остатком – .

2. и

│

Частным от деления на является многочлен , остатком – .

Это правило в общем виде можно сформулировать так:

1) разделить старший член многочлена f(x) на старший член g(x) и записать результат «под длинной стороной угла»;

2)умножить g(x) на результат действия 1) и записать произведение под многочленомf(x);

3) вычесть из f(x) записанный под ним многочлен;

4) проверить имеет ли результат действия 3) степень меньшую, чем степень g(x); если да (или результат нулевой), то он является остатком, а под длинной стороной угла записано частное, если нет, то применить к этому результату действие 1), рассматривая его как многочленf(x).

Я составила программу для нахождения частного и остатка.

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, StdCtrls, Grids;

type

TForm1 = class(TForm)

SGd1: TStringGrid;

Edit1: TEdit;

Edit2: TEdit;

Edit3: TEdit;

Edit4: TEdit;

Edit5: TEdit;

Edit6: TEdit;

Button1: TButton;

Label1: TLabel;

Label2: TLabel;

Label3: TLabel;

Label4: TLabel;

Label5: TLabel;

Label6: TLabel;

Label7: TLabel;

Label8: TLabel;

Label9: TLabel;

procedure Button1Click(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;

var

Form1: TForm1;

i,n,m,step,j,f:integer;

d,l,s:string;

a,a2,b,b2,k:array(0..100) of integer;

implementation

{$R *.dfm}

procedure TForm1.Button1Click(Sender: TObject);

begin

n:=StrToInt(Edit1.Text);

m:=StrToInt(Edit2.Text);

for i:=n+1 downto 1 do begin

a(i):=StrToInt(SGd1.Cells(n-(i-1),0));

end;

for i:=m+1 downto 1 do begin

b(i):=StrToInt(SGd1.Cells(m-(i-1),1));

end;

s:='f1(x)=';

for i:=n+1 downto 1 do begin

if a(i)<>0 then begin if(a(i-1)<0)or(i=1) then begin

str(a(i),l);

str(i-1,d);

s:=s+l+'x^'+d;

end

else begin

str(a(i),l);

str(i-1,d);

s:=s+l+'x^'+d+'+';

end;

end;

end;

Edit3.Text:=s;

s:='f2(x)=';

for i:=m+1 downto 1 do begin

if b(i)<>0 then begin if(b(i-1)<0)or(i=1) then begin

str(b(i),l);

str(i-1,d);

s:=s+l+'x^'+d;

end

else begin

str(b(i),l);

str(i-1,d);

s:=s+l+'x^'+d+'+';

end;

end;

end;

Edit4.Text:=s;

for j:=N+1 downto 1 do begin

a2(j):=a(j);

b2(j):=0;

end;

step:=n-m;

f:=n+2;

for i:=step+1 downto 1do begin

f:=f-1;

k(i):=a2(f);

for j:=m+1 downto 1do begin

b2(j):=k(i)*b(j);

end;

for j:=f downto 1 do begin

a2(j):=a2(j)*b(m+1);

end;

for j:=f downto 1 do begin

a2(j):=a2(j)-b2(j+1-i);

b2(j):=0;

end;

end;

s:='h(x)=';

for i:=f downto 1 do begin

if k(i)<>0 then begin if(k(i-1)<0)or(i=1) then begin

str(k(i),l);

str(i-1,d);

s:=s+l+'x^'+d;

end

else begin

str(k(i),l);

str(i-1,d);

s:=s+l+'x^'+d+'+';

end;

end;

end;

Edit5.Text:=s;

s:='r(x)=';

for i:=n downto 0 do begin

if a2(i)<>0 then begin if(a2(i-1)<0)or(i=1) then begin

str(a2(i),l);

str(i-1,d);

s:=s+l+'x^'+d;

end

else begin

str(a2(i),l);

str(i-1,d);

s:=s+l+'x^'+d+'+';

end;

end;

end;

Edit6.Text:=s;

end;

end.

2.3. Наибольший общий делитель многочленов

Пусть даны произвольные многочлены и . Многочлен будет называться общим делителем для и , если он служит делителем для каждого из этих многочленов. Свойство 5. показывает, что к числу общих делителей многочленов и принадлежат все многочлены нулевой степени. Если других общих делителей эти два многочлена не имеют, то они называются взаимно простыми.

В общем же случае многочлены и могут обладать делителями, зависящими от , и введем понятие о наибольшем общем делителе этих многочленов.

Наибольшим общим делителем отличных от нуля многочленов и называется такой многочлен , который является их общим делителем и, вместе с тем, сам делится на любой другой общий делитель этих многочленов. Обозначается наибольший общий делитель многочленов и символом .

Это определение оставляет открытым вопрос, существует ли наибольший общий делитель для любых многочленов и . Ответ на этот вопрос положительный. Существует метод для практического разыскания наибольшего общего делителя данных многочленов, называемый алгоритмом последовательного деления или алгоритмом Евклида.

2.4. Алгоритм Евклида

Алгоритм Евклида– метод для нахождения наибольшего общего делителя двух целых чисел, а также двух многочленов от одного переменного. Он первоначально был изложен в «Началах» Евклида в геометрической форме как способ нахождения общей меры двух отрезков. Алгоритм Евклида для нахождения наибольшего общего делителя, как в кольце целых чисел, так и в кольце многочленов от одного переменного является частным случаем некого общего алгоритма в евклидовых кольцах.

Алгоритм Евклида для нахождения наибольшего общего делителя двух многочленов и состоит в последовательном делении с остатком на , затем на первый остаток,затем на второй остаток и так далее. Так как степени остатков все время понижаются, то в этой цепочке последовательных делений мы дойдем до такого места, на котором деление совершится нацело и процесс остановится. Последний отличный от нуля остаток , на который нацело делится предыдущий остаток , и является наибольшим общим делителем многочленов и .

Для доказательства запишем изложенное в виде следующей цепочки равенств:

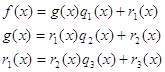
(2.4)

Последнее равенство показывает, что служит делителем для . Отсюда следует, что оба слагаемых правой части предпоследнего равенства делятся на , а поэтому будет делителем и для . Далее, таким же путем, поднимаясь вверх, мы получим, что является делителем и для , …, , . Отсюда ввиду второго равенства, будет следовать, что служит делителем для , а поэтому, на основании первого равенства, - и для .

Возьмем теперь произвольный общий делитель многочленов и . Так как левая часть и первое слагаемое правой части первого из равенств делятся на , то также будет делится на . Переходя ко второму и следующему равенствам, таким же способом получим, что на делятся многочлены , , … Наконец, если уже будет доказано, что и делятся на , то из предпоследнего равенства получим, что делится на . Таким образом, на самом деле будет наибольшим общим делителем для и .

Мы доказали, что любые два многочлена обладают наибольшим общим делителем, и получили способ его вычисления. Этот способ показывает, что если многочлены и имеют оба рациональные или действительные коэффициенты, то и коэффициенты их наибольшего общего делителя также будут рациональными или, соответственно, действительными, хотя у этих многочленов могут существовать и такие делители, не все коэффициенты которых рациональны (действительны).

Если есть наибольший общий делитель многочленов и , то, как показывают свойства 8. и 9., в качестве наибольшего общего делителя этих многочленов можно было бы выбрать также многочлен , где - произвольное число, отличное от нуля. Иными словами, их наибольший общий делитель двух многочленов определен лишь с точностью до множителя нулевой степени. Ввиду этого можно условиться, что старший коэффициент наибольшего общего делителя двух многочленов будет всегда считаться равным единице. Используя это условие можно сказать, что два многочлена тогда и только тогда взаимно просты, если их наибольший общий делитель равен единице. В самом деле, в качестве наибольшего общего делителя двух взаимно простых многочленов можно взять любое число, отличное от нуля, но, умножая его на обратный элемент, получим единицу.

Применяя алгоритм Евклида к многочленам с целыми коэффициентами, можем, чтобы избежать дробных коэффициентов, умножить делимое или сократить делитель на любое не равное нулю число, причем не только начиная какое-либо из последовательных делений, но и в процессе самого этого деления. Это будет приводить к искажению частного, но интересующие нас остатки будут приобретать лишь некоторый множитель нулевой степени, что при разыскании наибольшего общего делителя допускается.

Пример. Найти наибольший общий делитель многочленов и .

1. и

Совершим требуемые деления с остатком:

|

|

|

Построение последовательности Евклида закончено. Ее последний член есть наибольший общий делитель исходных многочленов.

2. и

Совершим требуемые деления с остатком:

│

‌‌‌‌‌‌‌‌‌ || ‌

│

│

Построение последовательности Евклида закончено. Ее последний член есть наибольший общий делитель исходных многочленов.

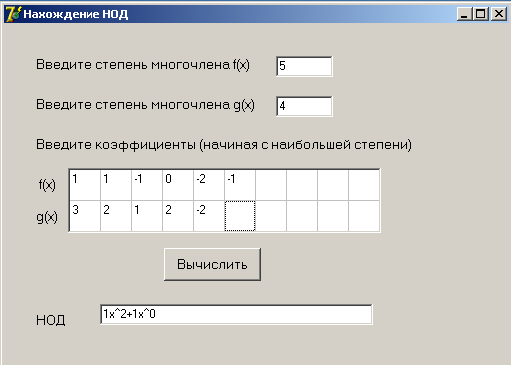
Я составила программу для нахождения наибольшего общего делителя двух многочленов:

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, StdCtrls, Grids;

type

TForm1 = class(TForm)

Label1: TLabel;

Label2: TLabel;

Edit1: TEdit;

Edit2: TEdit;

SGd1: TStringGrid;

Label3: TLabel;

Button1: TButton;

Label4: TLabel;

Edit4: TEdit;

Label5: TLabel;

Label6: TLabel;

procedure Button1Click(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;

var

Form1: TForm1;

st1,st2:integer;

kof1,kof2,k1,k2:array(0..10) of integer;

implementation

{$R *.dfm}

procedure TForm1.Button1Click(Sender: TObject);

var i,j,k_1,st3,l:integer;

sokr:boolean;

k2_2,k1_1:array(0..10) of integer;

begin

st1:=StrToInt(Edit1.Text);

st2:=StrToInt(Edit2.Text);

for i:=0 to st1 do begin

kof1(i):=StrToInt(SGd1.Cells(i,0));

k1(i):=StrToInt(SGd1.Cells(i,0));

end;

for i:=0 to st2 do begin

kof2(i):=StrToInt(SGd1.Cells(i,1));

k2(i):=StrToInt(SGd1.Cells(i,1));

end;

while kof2(0)<>0 do begin

repeat

Edit4.Text:='';

k_1:=k1(0);

if k1(0)<>kof2(0) then begin

if (k1(0) mod kof2(0))=0 then begin

for j:=0 to st2 do

k2(j):=(k1(0) div kof2(0))*kof2(j);

end

else begin

if k2(0)<>1 then

for j:=0 to st1 do

k1(j):=kof2(0)*k1(j);

if k_1<>1 then begin

for j:=0 to st2 do

k2(j):=k_1*kof2(j);

end;

end;

end;

for i:=1 to st1 do begin

k1(i-1):=k1(i)-k2(i);

end;

st1:=st1-1;

until st1

if k1(0)<>0 then begin //Сокращение

sokr:=true;

for i:=1 to st1 do

if k1(i)<>0 then begin

if (k1(i) mod k1(0))<>0 then sokr:=false;

end;

k_1:=k1(0);

if sokr=true then

for i:=0 to st1 do

k1(i):=k1(i) div k_1;

end;

for i:=0 to st2 do //Замена многочленов

k2_2(i):=kof2(i);

for i:=0 to st1 do

k1_1(i):=k1(i);

for i:=0 to 10 do begin

kof1(i):=0;

k1(i):=0;

kof2(i):=0;

k2(i):=0;

end;

for i:=0 to st2 do begin

k1(i):=k2_2(i);

if k1(i)<>0 then

Edit4.Text:=Edit4.Text+IntToStr(k1(i))+'x^'+IntToStr(st2-i);

if (k2_2(i+1)>0)and(i

end;

for i:=0 to st1 do begin

k2(i):=k1_1(i);

kof2(i):=k1_1(i);

end;

st3:=st1;

st1:=st2;

st2:=st3;

end;

end;

end.

Используем алгоритм Евклида для доказательства следующей теоремы:

Теорема. Если есть наибольший общий делитель многочленов и , то можно найти такие многочлены и , что

. (2.5)

Можно считать при этом, если степени многочленов и больше нуля, что степень меньше степени , а степень меньше степени .

Доказательство основано на равенствах (2.4). Если учтем, что , и положим , , то предпоследнее из равенств (2.4) даст:

.

Подставляя сюда выражение через и из предшествующего равенства (2.4), получим:

,

где , . Продолжая подниматься вверх по равенствам (2.4), придем к доказываемому равенству (2.5).

Для доказательства второго утверждения теоремы предположим, что многочлены и , удовлетворяющие равенству (2.5), уже найдены, но, например, степень больше или равна степени . Делим на :

,

где степень меньше степени , и подставляем это выражение в (2). Получим равенство:

.

Степень множителя, стоящего при , уже меньше степени . Степень многочлена, стоящего в квадратных скобках, будет в свою очередь меньше степени , так как в противном случае степень второго слагаемого левой части была бы не меньше степени , а так как степень первого слагаемого меньше степени этого произведения, то вся левая часть имела бы степень, большую или равную степени , тогда как многочлен заведомо имеет, при наших предположениях, меньшую степень.

Теорема доказана.

Одновременно получаем, что если многочлены и имеют рациональные или действительные коэффициенты, то и многочлены и , удовлетворяющие равенству (2.5), можно подобрать так, что их коэффициенты будут рациональными или, соответственно действительными.

Применяя доказанную теорему к взаимно простым многочленам, получаем такой результат:

Многочлены и тогда и только тогда взаимно просты, если можно найти многочлены и , удовлетворяющие равенству

. (2.6)

Опираясь на этот результат, можно доказать несколько простых, но важных теорем о взаимно простых многочленах:

Теорема 1. Если многочлен взаимно прост с каждым из многочленов и , то он взаимно прост и с их произведением.

Доказательство. В самом деле, существуют, по (2.6), такие многочлены и , что .

Умножая это равенство на , получаем:

,

откуда следует, что всякий общий делитель и был бы делителем и для ; однако по условию .

Теорема 2. Если произведениемногочленов и делится на , но и взаимно просты, то делится на .

Доказательство. Умножая равенство на , получим: .

Оба слагаемых левой части этого равенства делятся на ; на него делится, следовательно, и .

Теорема 3. Если многочлен делится на каждый из многочленов и , которые между собой взаимно просты, то делится и на их произведение.

Доказательство. Действительно, , так что произведение, стоящее справа, делится на . Поэтому, по теореме 2, делится на , , откуда .

Определение наибольшего общего делителя может быть распространен на случай любой конечной системы многочленов: наибольшим общим делителем многочленов называется такой общий делитель этих многочленов, который делится на любой другой общий делитель этих многочленов. Существование наибольшего общего делителя для любой конечной системы многочленов вытекает из следующей теоремы, дающей также способ его вычисления.

Теорема. Наибольший общий делитель многочленов равен наибольшему общему делителю многочлена и наибольшего общего делителя многочленов .

Доказательство. В самом деле, при теорема очевидна. Примем поэтому, что для случая она справедлива, то есть, в частности, уже доказано существование наибольшего общего делителя многочленов . Обозначим через наибольший общий делитель многочленов и . Он будет общим делителем для всех заданных многочленов. С другой стороны, всякий другой общий делитель этих многочленов будет делителем также и для , а поэтому и для .

В частности, система многочленов называется взаимно простой, если общими делителями этих многочленов являются лишь многочлены нулевой степени, то есть если их наибольший общий делитель равен 1. Если , то попарно эти многочлены могут и не быть взаимно простыми.

Теорема Безу. Многочлен f(x) делится на x-c тогда и только тогда, когда число c является его корнем.

Рассмотрим произвольный многочлен f(x) и разделим его с остатком на двучлен x-c. Поскольку степень этого двучлена равна 1, то остаток либо равен 0, либо имеет степень 0. И в том, и в другом случае остаток rесть число. Таким образом, многочлен f(x) представляется в виде:

f(x)= (x-c) q(x)+ r.

Положив в этом тождестве x= c, получим что f(c)=r. Мы доказали тем самым, что остаток от деления многочлена на двучленx- cравен значению многочлена приx=c.

С помощью теоремы Безу решим несколько задач.

Пример 1. Решить уравнение .

Многочлен f(x)= имеет корень 2. По теореме Безу f(x) делится на x-2, то есть имеет место равенство

.

|

Остается решить квадратное уравнение .

Это уравнение не имеет действительных корней, так что x=2 – единственный действительный корень исходного уравнения.

2. Решить уравнение .

Многочлен f(x)= имеет корень -2. По теореме Безу f(x) делится на x+2, то есть имеет место равенство .

|

0

Остается решить квадратное уравнение .

Это уравнение имеет корень 1. Так что x=-2 и x=1 – корни исходного уравнения.

Если c – корень многочлена f(x), то есть f(c)=0, то f(x) делится на x-c. Может оказаться, что многочлен f(x) делится не только на первую степень линейного двучлена x-c, но и на более высокие его степени. Во всяком случае, н