Анализ динамических свойств системы автоматического управления заданной структурной схемы

Проектирование автоматики - одно из наиболее сложных и важных направлений в инженерной деятельности, поэтому знание основ автоматики, представление об уровне автоматизации в различных технологических процессах, используемых средствах автоматизации и основах проектирования являются необходимыми условиями успешной работы инженеров и технологов. Нормальное ведение любого технологического процесса характеризуется определенными значениями параметров, а экономическая и безопасная работа оборудования обеспечивается поддерживанием эксплуатационных параметров в требуемых пределах. Для целей нормальной эксплуатации оборудования, а также осуществления требуемого технологического процесса в любых тепловых установках необходимо в проектных разработках предусматривать и средства автоматизации. В настоящее время во всех отраслях народного хозяйства, включая и сельское хозяйство, все большее применение находят системы автоматического управления. Это и не удивительно, так как автоматизация технологических процессов характеризуется частичной или полной заменой человека оператора специальными техническими средствами контроля и управления. Механизация, электрификация и автоматизация технологических процессов обеспечивают сокращение доли тяжелого и малоквалифицированного физического труда в сельском хозяйстве, что ведет к повышению его производительности.

Таким образом, необходимость автоматизации технологических процессов очевидна и есть необходимость научиться рассчитывать параметры систем автоматического управления (САУ), для последующего применения своих знаний на практике.

В курсовой работе произведен анализ динамических свойств заданной структурной схемы САУ с составлением и анализом математических моделей объектов управления.

2. Анализ динамических свойств заданной структурной схемы

2.1 Анализ устойчивости САУ по критерию Найквиста

Для суждения об устойчивости САУ нет необходимости в определении точный значений корней её характеристического уравнения. Поэтому полное решение характеристического уравнения системы явно излишне и можно ограничиться применением того или иного косвенного критерия устойчивости. В частности нетрудно показать, что для устойчивости системы необходимо (но не недостаточно), чтобы все коэффициенты её характеристического уравнения имели одинаковый знак или достаточно, чтобы действительные части всех корней характеристического уравнения были отрицательными. В случае, если действительные части всех корней характеристического уравнения не отрицательны, то для определения устойчивости этого САУ необходимо исследование и по другим критериям, так как если передаточная функция по вышеназванному критерию принадлежит к неустойчивому блоку, у которых знаменатель имеет корни с положительной действительной частью, то при выполнении определенных условий замкнутая система и в этом случае может быть устойчивой.

Наиболее удобным для исследования устойчивости многих систем управления технологическими процессами является критерии устойчивости Найквиста который формируется следующим образом.

Система, устойчивая в разомкнутом состоянии, сохранит устойчивость и после её замыкания отрицательной обратной связью, если годограф КЧХ в разомкнутом состоянии W(jω) не охватывает в комплексной плоскости точку с координатами (-1;j0).

В приведенной формулировке критерия Найквиста считается, что годограф КЧХ W(jω) «не охватывает» точку (-1;j0), если равен нулю общий угол поворота вектора проведенный из указанной точки к годографу W(jω) при изменении частоты от ω=0 до ω → ∞.

Если годограф КЧХ W(jω) при некоторой частоте называемой критической частотой ωк, проходит через точку (-1;j0), то переходный процесс в замкнутой системе представляет собой незатухающие колебания с частотой ωк , т.е. система оказывается на границе устойчивости выраженные следующим образом:

W(jω)= -1.

Структурная схема замкнутой линейной САУ показана на рисунке 2.

Рисунок 2 Замкнутая САУ

Здесь W(p) – передаточная функция разомкнутой САУ. Предположим, что разомкнутая система устойчива. Тогда для устойчивости замкнутой САУ необходимо и достаточно, чтобы годограф амплитудно-фазовой характеристики W(jw) разомкнутой системы (указанная характеристика получается из W(p) заменой p=jw) не охватывал точку с координатами (-1, j0). Частота, на которой |W(jw)| = 1, называется частотой среза (w_ср).

Для оценки насколько далеко от границы устойчивости находится система, вводятся понятие запасов устойчивости. Запас устойчивости по амплитуде (модулю) указывает, во сколько раз необходимо изменить длину радиуса-вектора годографа АФХ, чтобы, не меняя фазового сдвига, вывести систему на границу устойчивости. Для абсолютно устойчивых систем запас устойчивости по модулю DК вычисляется по формуле:

где частота w⁰ определяется из соотношения arg W(jw⁰) = - 180⁰.

Запас устойчивости по амплитуде DК вычисляется и по формуле:

DК = 1 - К₁₈₀ ;

где К₁₈₀ - значение коэффициента передачи при фазовом сдвиге -180°.

В свою очередь, запас устойчивости по фазе указывает, на сколько необходимо увеличить по абсолютной величине аргумент АФХ, чтобы, не меняя величину модуля, вывести систему на границу устойчивости.

Запас устойчивости по фазе Dj вычисляется по формуле:

Dj = 180° - j_К=1 ;

где j_К=1 - значение фазового сдвига при коэффициенте передачи К = 1;

Величина Dj = 180⁰ + arg W(j;w_ср) определяет запас устойчивости по фазе. Из критерия Найквиста следует, что устойчивая в разомкнутом состоянии САУ будет устойчивой и в замкнутом состоянии, если сдвиг по фазе на частоте среза не достигает - 180°. Выполнение этого условия можно проверить, построив логарифмические частотные характеристики разомкнутой САУ.

2.2 Исследование устойчивости САУ по критерию Найквиста

Исследование устойчивости по критерию Найквиста путем анализа АФЧХ при разомкнутой САУ. Для этого разрываем систему как показано на структурной схеме исследуемой САУ:

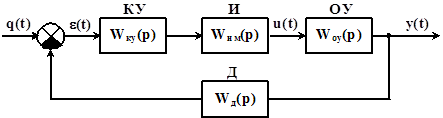
Рисунок 3 Структурная схема исследуемой САУ

Ниже представлены передаточные функции объекта управления (ОУ), исполнительного механизма (ИМ), датчика (Д) и корректирующего устройства (КУ):

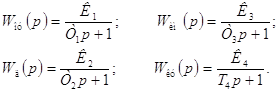
Значения коэффициентов по заданию следующие:

К1 =1,0; К2 = 0,2; К3 = 2; К4 = 1,0; Т1 = 0,4; Т2 = 0,2; Т3 = 0,07; Т4 = 0,4.

Произведем расчет передаточной функции после разрыва системы:

W(р) = W_ку(р) × W_им(р) ×W_оу(р) ×W_д(р);

W(р) = ×××

Подставив заданные коэффициенты в функцию получим:

W(р) =

Анализируя данную функцию в программе математического моделирования («МАТLАВ»), получим годограф амплитудно-фазочастотной характеристики (АФЧХ) разомкнутой САУ на комплексной плоскости, приведенную на рисунке 4.

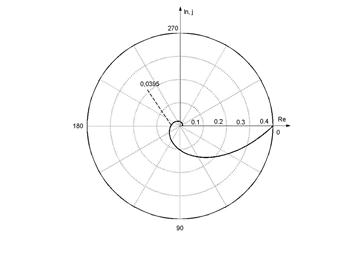
Рисунок 4 Годограф АФЧХ разомкнутой САУ на комплексной плоскости.