Расчет характеристик обнаружения при совместном когерентном и некогерентном накоплении
Задание № 4. Расчет характеристик обнаружения при совместном когерентом и некогерентном накоплении.
Рассматривается задача обнаружения сигнала (в виде пачки прямоугольных импульсов) на фоне внутренних шумов приемника, распределенных по гауссовскому закону.
При обнаружении реализуется дополнительное некогерентное накопление когерентного сигнала: ранее сформированные пачки прямоугольных когерентных импульсов некогерентно накапливаются в течение нескольких тактов Tнкн = М tT = М tкн , где М - число тактов некогерентного накопления, tT = tкн - длительность каждого такта. При этом используется критерий “m из M”, т.е. обнаружение сигнала считается состоявшимся (достоверным), если установленный порог превышен не менее чем в “m” т из “M” тактах.
Заданные диапазоны изменения параметров сигнала:
ü высокая частота повторения (ВЧП)-Fп= 100-300 кГц; Tнкн = М tкн , М = (3-15);
ü Qпрд = 4-10; 
= 0,3- 2,5 мкс; tкн = 3-30 мс; Tнкн = (3-15) tкн;
ü средняя частота повторения (СЧП) -- Fп= 10-50 кГц;
ü Qпрд = 10-50; , τ и = 0,4-10 мкс; tкн = 3-30 мс; Tнкн = (3-15) tкн;
ü низкая частота повторения (НЧП) - Fп= 5–10 кГц;
ü Qпрд = 50–100; 
, τ и = 0,2–4 мкс; tкн = 3–30 мс; Tнкн = (3-15) tкн;
Здесь обозначено: Fп–частота повторения зондирующих импульсов; Qпрд–скважность излучаемых сигналов; τи–длительность зондирующих импульсов; tкн–время когерентного накопления; Tнкн– время некогерентного накопления М - число тактов некогерентного накопления.
1. В качестве заданных значений вероятности правильного обнаружения (
) использовать значения – 0,2; 0,5; 0,7; 0,8; 0,9; 0,95. При расчетах заданных значений вероятностей ложных тревог (
) исходить из того, что за “время наблюдения- Tлт” (Tлт =1 мин) допускается не более, чем одна ложная тревога. Тогда справедливо соотношение: 
. Расчет произвести для всех вариантов когерентного сигнала, рассмотренных в задании 3 (ВЧП, СЧП, НЧП.)
2. Рассчитать вероятности правильного обнаружения (
) и ложной тревоги (
), обеспечиваемые при совместном когерентном и некогерентном накоплении сигнала. При этом использовать формулу Бернулли:
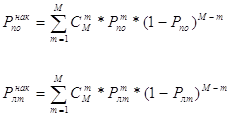
Расчет произвести для M=3; 5; 7; 9; 11; 13; 15 и для 
.
3. Сравнить полученные значения и с заданными значениями и .
4. Сравнить характеристики обнаружения при когерентном и некогерентном накоплении:
ü “по вероятностям” (Pпо, Pлт, ,) – при одинаковых q и qпор;
ü “по энергетике” (q, qпор) – при одинаковых Pпо, Pлт, , .
5. Оценить выигрыш, обеспечиваемый при совместном когерентном и
некогерентном обнаружении по сравнению с раздельным накоплением и с приемом одиночного сигнала (см. задания 1-3).
Наибольший интерес представляют 3 области:
§ I- область “низкой достоверности” (при совместном выполнении условий обнаружения ≤ 0,2, = 10– 1-10– 2);
§ II- “область средней достоверности” (при совместном выполнении условий 0,2 < ≤ 0,7, = 10– 2-10– 4);
§ III- “область высокой достоверности” (при совместном выполнении условий > 0,7, = 10– 4-10– 8).
6 Проанализировать полученные результаты. Сделать выводы.
.7. Рекомендуемая литература:
§ Теоретические основы радиолокации. Под ред. Я.Д. Ширмана, М.:Сов. радио, 1970;
§ РЭС: основы построения и теория. Справочник. Под ред Я.Д. Ширмана,- М.:ЗАО “МАКВИС”, 1998;
§ Сосулин Ю.Г. Теоретические основы радиолокации и радионавигации.- М.: Радио и связь, 1994.
- Бакулев П.А., Сосновский А.А. Радиолокационные и радионавигационные системы. - М.: Радио и связь, 1994.
8. При выполнении курсового проекта расчеты производить в среде Matlab с применением модульного принципа.