Принцип Маха и космологическое происхождение инерции

Садыков Б.С.

Введение

Инерция, пожалуй, одно из самых загадочных явлений макромира. Неизвестно, как она возникает, где ее источники и почему она такая какая есть /1/. Все живое рождается с заранее закодированной в памяти информацией об инерции. Сидя в машине, мы точно знаем, что на повороте возникает центробежная сила, которая будет прижимать нас к боковой стенке машины и тут же исчезает как только машина завершит разворот и выйдет на прямую ровную дорогу. Она снова возникает при торможении, но теперь толкает нас вперед, а при рывке – назад. Мы с инерцией сталкиваемся ежедневно и к ней так привыкли что ее воспринимаем как неизбежность, как реальность, которая не требует объяснения, поэтому нас не удивляет ни ее внезапное появление, ни бесследное исчезновение, ни отсутствие видимого контакта.

В кинематическом отношении инерция ничем не отличается от гравитации, такая же универсальная, так же сообщает всем телам одинаковое ускорение, так же не имеет ни точек опоры, ни приложения. Поэтому неудивительно, что Эйнштейн их отождествил. Аргументы Эйнштейна известны: гравитационная масса является источником сил гравитации, а инертная – индикатором инерции. Эти массы равны, а следовательно, должны быть равны и индуцируемые ими силы. Аргументы обоснованные, но из них вовсе не следует, что «инерция и гравитация являются разными названиями одного и того же явления». Гравитационные силы потенциальные, ослабевают по мере удаления от гравитирующих тел в то время как силы инерции не потенциальные и не зависят от каких-либо расстояний. Эти силы разные по природе и должны быть разделены /2/.

Обобщенный принцип Маха

Единственной гипотезой которая в какой-то степени связывает инерцию с материей, является принцип Маха (ПМ). Чтобы понять его смысл применительно к инерции, приведем конкретный пример Пусть заданы два массивных тела, с которыми связаны системы отсчета (СО) S и . Предположим система покоится, а вращается относительно нее с некоторой угловой скоростью. Из опыта знаем, что в покоящейся СО силы инерции не возникают, а во вращающейся возникают независимо от покоящейся системы. Это странное несоответствие, противоречащее понятию относительности движения. Если вращение относительно вызывает в силы инерции, то такие же силы должны возникать и в поскольку и она вращается относительно . Однако этого не происходит. Почему? Откуда взялись эти силы и почему только в одной системе, если S и в кинематическом отношении совершенно равноправны? Единственно разумный ответ может дать только ПМ. Он утверждает, что система покоилась не одна, а вместе со всеми телами Вселенной Они вместе образовали единую глобальную систему отсчета и система вращалась относительно этой глобальной системы. Следовательно, силы инерции возникли бы и в, если бы вокруг нее вращалась, т.е. вся Вселенная! Мы не можем экспериментировать со Вселенной, чтобы подтвердить или опровергнуть справедливость ПМ. В этом смысле ПМ остается недоказуемой и ничем необоснованной гипотезой поскольку, словесно декларируя космологическое происхождение инерции, не объясняет механизм ее формирования. Поэтому неизвестно каким образом звезды, удаленные на миллионы световых лет, формируют инерцию здесь, на Земле и, если формируют то как определить их инерцетворную способность.

Чтобы исключить эту неопределенность и придать ПМ количественное выражение, нами выдвинута дополнительная гипотеза, согласно которой всякое тело при движении, наряду с гравитационным полем, создает еще одно поле, такое что его изменение индуцирует инерцию. Назовем его «инерционным». Применительно к ПМ это означает, что небесные тела, двигаясь относительно друг друга, генерируют особое, так называемое «инерционное поле». Оно заполняет все пространство, образуя некоторую квазиупругую среду, препятствующую ускоренному движению. Реакция этой среды на действия сил, стремящихся изменить состояние тела, есть отклик Вселенной который воспринимается как инертность тела.

В дальнейшем под «ПМ» понимается это обобщение. Физические соображения, лежащие в основе этой гипотезы, частично были изложены ранее /3,4/ и вкратце будут повторены здесь.

1. Уравнение движения в неинерциальных системах отсчета

Основной величиной, содержащей необходимую информацию об инерции, является сама сила инерции . Она входит в уравнения движения тела в неинерциальных системах отсчета (НИСО) , как внешняя сила без определенного источника. Пусть - импульс этой силы. Учитывая, что он всегда направлен против сил, стремящихся изменить состояние тела, представим его в виде

, , (1.1)

При таком представлении силы инерции как бы исчезают, но механический импульс приобретает дополнительный компонент, определяющий взаимодействие движущегося тела со всеми телами Вселенной. Взаимодействие носит полевой характер, поэтому его можем постулировать как сумму произведений всевозможных зарядов(электрических, гравитационных и др.) движущегося тела и 4-векторных потенциалов соответствующих полей , создаваемых другими телами

, (1.2)

где -потенциальная энергия, - скорость света. Каждый вид заряда qn, который способен в состоянии покоя создавать статическое поле Еn, при движении создает еще и динамическое поле Нn.. Последнее возникает, как следствие двух фундаментальных законов природы: закона обратных квадратов, приводящего к уравнению Пуассона

divЕn =кn rn =sn , (1.3)

и закона сохранения заряда:

, (1.4)

где и - плотность и поток зарядов , - соответствующая константа связи. Комбинируя (1.3) и (1.4), получим:

, (1.5)

Аргумент дивергенции либо константа либо является ротором вихревого поля движущегося потока зарядов . Первый аргумент физически неприемлем, из второго имеем:

, (1.6)

Динамическое поле электрического заряда хорошо известно - это магнитное поле, а какие поля создают другие виды зарядов, в частности гравитационный, пока неизвестно, но их реальность гарантируется двумя фундаментальными законами физики (1.3) и (1.4). На этом и основана наша гипотеза, которая по сути означает, что всякое тело при движении наряду с гравитационным полем индуцирует еще одно, ранее неизвестное динамическое поле, которое мы и назвали инерционным.

Чтобы понять смысл динамических полей и их роль в системе мироздания, составим уравнение движения. Будем исходить из уравнения Лагранжа

(1.7)

с лагранжианом, образованным из квадрата импульса взаимодействий

L = (р+П)2 + (р4 + П4 )2 , (1.8)

Выполняя стандартные расчеты, получим

(1.9)

где , ,

, (1.10)

Из этих определений следует очень важный закон - закон обобщенной индукции

, , (1.11)

Он утверждает что, силы инерции имеют индукционную природу и индуцируются вихревым полем , которое создается всеми движущимися телами Вселенной. Всякое тело, попадая в это поле, приобретает дополнительный момент импульса («инертный момент»)

(1.12)

и вынуждено вращаться. Действие вихревого поля эквивалентно действию сил инерций, которые возникают в НИСО вращающейся с угловой скоростью

(1.13)

Если на тело другие силы не действуют, то оно будет вращаться с угловой скоростью, равной Покажем это на конкретном примере. Пусть движущееся тело, помимо гравитационного заряда (массы ), других зарядов не имеет, тогда

, ,

Разлагая силу на продольную и поперечную составляющие, получим

(1.14)

, (1.15)

где- гравитационный потенциал. Первое уравнение определяет инерцию, вызванную изменением скорости по величине, второе – по направлению. В первом выражении ускорение состоит из суммы двух ускорений, ускорение вызванное силами инерции и гравитационным полем. Они коллинеарны, поэтому наблюдатель, находящийся в замкнутом пространстве, например в лифте, не может определить какая из этих двух сил на него действует: гравитационная или инерции. Они неразличимы. Эту неразличимость Эйнштейн назвал «принципом эквивалентности» и положил в основу ОТО.

Вторая сила напоминает уравнение Эйлера для движения тела во вращающейся НИСО. Первый член описывает инерцию, вызванную неравномерностью вращения, второй кориолисову силу, третий – центробежную. Принципиальное отличие состоит в том, что здесь означает не угловую скорость вращения, а индукцию инерционного поля! Она имеет размерность угловой скорости и этим создает ложное представление как будто она обозначает механическое вращение. Совпадение означает, что тело в инерционном поле, приобретает угловую скорость численно равную индукции инерционного поля в данной точке. Инерционное поле оказывает на гравитационный заряд точно такое действие какое оказывает магнитное поле на электрический заряд. В механике инерционное поле играет ту же роль что и магнитное поле в электродинамике, поэтому должно быть включено в описании всякого движения. Тогда все трудности, связанные с нарушениями законов механики в НИСО (третий закон Ньютона, законы сохранения, абсолютность ускорения и др.), снимаются.

Если изменение вихревого поля индуцирует потенциальное поле, то ввиду относительности движения, должен существовать и обратный эффект. Изменение потенциального поля должно порождать вихревое поле. Такой эффект действительно существует. Умножая (1.6) на соответствующие константы связи, получим

, (1.16)

,

Угловые скобки означают усреднение скорости потока. Уравнения (1.11) и (1.16) образуют единую самосогласованную систему которую будем называть «уравнениями инерцодинамики». Входящие в эту систему поля связаны со статическимии динамическими полями и их индукциями , соотношениями

, ,

(1.17)

,

Отношения констант связи определяет скорость распространения отдельных полей

, (1.18)

а их комбинация , (1.19)

- скорость центра группы парциальных волн.

Уравнения (1.11) и (1.16) составлены из П-импульса и его производных и могут быть представлены в общековариантной форме

, (1.20)

где (1.21)

Уравнения подобного типа хорошо известны и в комментариях не нуждаются. Зная скорость движения тела всегда можем вычислить индуцируемое им инерционное поле. Тем самым задача по определению механизма возникновения инерции и ее источников полностью решена. Рассмотрим ряд частных случаев

2. Объединенная система уравнений электродинамики и гравидинамики

Рассмотрим движение электрически заряженной частицы в поле, создаваемое аналогичными частицами. Частица несет два вида заряда - электрического и гравитационного (массы) . Полагая , получим

, , (2.1)

где - напряженности электрического и гравитационного полей, - векторы магнитной и инерционной (гравимагнитной) индукций. Траектория движения частицы в этих полях зависит от их отношения. В микромире грави-инерционные силы чрезвычайно слабые и практически никакой роли не играют. Пренебрегая им из (1.11) и (1.16) автоматически получим систему уравнений электродинамики Максвелла – Лоренца. В мегамире, наоборот, они доминируют. В этом случае можно пренебречь электромагнитными силами, тогда получим аналогичную систему уравнений для гравидинамики

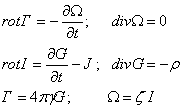(2.2)

где и - плотность и поток массы, g и z - константы связи гравитационного и гравимагнитного полей. Судьба этих уравнений драматична. Они в разной форме предлагались многими выдающимися физиками (Максвелл, Герц, Хэвисайд, Пуанкаре, Бриллюэн и др./5/), но признания не получили. Называют разные причины: отсутствие отрицательного гравитационного заряда, зависимость массы от скорости, неспособность линейной теории объяснить эффекты ОТО и др. Но все-таки, на наш взгляд, истинной причиной были не они, а неопределенность гравимагнитного поля, точнее отсутствие каких-либо явлений, которые свидетельствовали бы о наличии такого поля. Наблюдаемые явления, вроде бы, объяснялись и без него и в нем не было никакой необходимости. Такая природная невостребованность привела к сомнениям в реальности гравимагнитного поля и системы уравнений (2.2) в целом. Теперь эта неопределенность устранена. Получена система обобщенных уравнений из которой уравнения (2.2) вытекают как следствие. При этом гравимагнитное поле приобретает определенный смысл. Оно выражает напряженность инерционного поля . В гравидинамике она играет ту же роль, что и магнитное поле в электродинамике. Гравитационное и инерционное поля взаимосвязаны, друг друга индуцируют и распространяются в виде поперечных волн со скоростью

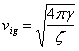, (2.3)

Величина этой скорости пока неизвестна, но есть ряд косвенных доказательств того, что в вакууме она совпадает со скоростью света. Принимая это как модель, определим «инерционную постоянную вакуума»

м/кг (2.4)

Это – чрезвычайно малая величина. Ее малостью можно объяснить почему инерционные поля обычных тел не наблюдаются. Они велики лишь в масштабе Вселенной и играют важную роль в формировании ее структуры. Разумеется, плотной среды гораздо выше вакуумной, но пока мы о них ничего не знаем.

3. Эффекты ОТО и новый грави-инерционный эффект

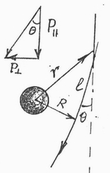
Три эффекта – гравитационное смещение спектра, отклонение луча в поле тяготения и вращение перигелия планет – обычно интерпретируются как отклонение от закона Ньютона. Первый эффект тривиален и вытекает из закона сохранения энергии фотона. Второй также вытекает из закона

Ньютона (рис.1)

, (3.1)

но угол отклонения в два раза меньше наблюдаемого. В ОТО это объясняется кривизной пространства. В данном случае кривизна мала и учтена законом Ньютона, поэтому неизвестна, откуда берется вторая половина. Покажем, что она связана с действием инерционного поля. На луч света, проходящего мимо массивного тела с массой на расстоянии , действуют две силы: ньютоновская , которая вызывает отклонение (3.1) и инерционная (гравилоренцовая) , которая под действием инерционного поля тела

(3.2)

вызывает дополнительное отклонение на угол

, (3.3)

Если заменить ее значением из (2.4), то этот угол совпадет с ньютоновским. Совпадение формально можно было бы рассматривать как согласие с ОТО. Однако, это не так. Дело в том, что эти углы находятся в разных плоскостях. Первый определяет отклонение луча в радиальном направлении, второй – в аксиальном. Во втором случае луч не притягивается к телу, а отбрасывается инерционным полем в сторону. (рис.2)

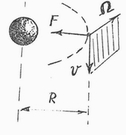
Он стремится вращаться вокруг силовых линий инерционного поля, но ввиду его слабости, траектория луча не замыкается и он, описав винтовую линию с большим шагом, покидает поле. Наблюдатель видит его проекцию на направление к телу и принимает его за дополнительное отклонение. Его впервые наблюдал Эдингтон в 1919 г. во время солнечного затмения, но считал его погрешностью эксперимента. Спустя три года такое же смещение обнаружили Кэмпбелл и Трюмплер, а затем и другие исследователи. В 1973 г. Джонес зафиксировал уже смещение 39 звезд и стало ясно, что аксиальное такая же реальность, как и радиальное смещение (более подробно см. обз./6/).

Рассмотрим третий эффект - вращение перигелия планет Пусть мимо массивного тела движется малое тело. Если инерционное поле достаточно сильное, то оно захватывает тело и заставляет его вращаться вокруг его силовых линий. Предположим поле захватило тело и вращение происходит по эллипсу с периодом обращения . Если поле создано только взаимным вращением, то

, (3.4)

где-средний радиус эллиптической орбиты тела с большой полуосью и эксцентритетом . Вращающееся тело, помимо механического момента импульса , обладает еще инертным моментом . Он в два раза меньше механического и направлен в ту же сторону что и . Тело с общим моментом 3 в инерционном поле (3.4) будет прецессировать с «гравиларморовской» частотой и через каждый оборот смещаться по направлению движения на угол

, (3.5)

который так же совпадает с данными ОТО. Два последних эффекта содержат константу инерционного взаимодействия и подтверждены наблюдениями. Их можно рассматривать как количественное подтверждение реальности инерционного поля.

4. Вращение небесных тел и архитектура Вселенной

В современной космологии причины вращения небесных тел обычно не рассматриваются. Предполагается, что тела приобрели нужный импульс каким-то образом после Большого взрыва. Возможно в процессе эволюции тела какие-то импульсы получали, но они были случайными и не могли обеспечить наблюдаемый порядок. Вращение настолько широко распространенное и закономерное явление, что объяснить его каким-то случайным толчком не представляется возможным. Оно должно иметь постоянно действующий источник. Им может быть только инерционное поле.

Рассмотрим такую ситуацию. Предположим некоторым объектом, скажем Галактикой, создано мощное инерционное поле и в его центре оказалось очень массивное тело, типа Солнца. Пусть другое, менее массивное тело, двигаясь с некоторой скоростью пересекает силовые линии -поля под некоторым углом. На него будет действовать грави-инерционная сила.

(4.1)

Обратим внимание на уравнение движения (1.9). Оно содержит множитель , который определяется отношением потенциальной энергии частицы (тела) к ее энергии покоя и указывает, что закон обратных квадратов в сильных полях не выполняется и должен быть заменен на

К аналогичным выражениям приводит и ОТО, однако в ОТО поправка касается только гравитационному взаимодействию, а здесь она носит общий характер, т.е, относится и закону Кулона. В данной работе она считается малой и не учитывается ).

Выберем систему координат так чтобы .Учитывая, что из (4.1), получим

, , , (4.2)

где - гравитационный потенциал. Эти уравнения с начальным условием имеют частное решение

, , , (4.3)

которое показывает, что сильное поле захватывает тело и вынуждает его вращаться вокруг его силовых линии с угловой скоростью . Одновременно тело под действием гравитационного поля начнет дрейфовать к центру тяготения. Дрейф происходит по винтовой линии. Если траектория проходит на достаточном удалении от поверхности массивного тела, то малое тело по инерции пересекает экваториальную плоскость массивного тела и попадает в зону гравитационного торможения. Постепенно его скорость уменьшается до нуля, а затем после мгновенной остановки, тело начнет обратное движение. Оно снова пересекает экваториальную плоскость, попадает в зону торможения и процесс повторяется. (рис.3)

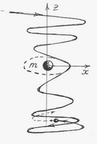
После нескольких переходов «вверх вниз» колебание затухает и тело окажется в экваториальной плоскости массивного тела. Здесь оно приобретает постоянную орбиту и становится спутником. То же самое происходит со всеми телами, откуда бы они не двигались. Все они соберутся в этой плоскости. На пути дрейфа возможны столкновения с другими телами. В этом случае крупные тела раскалываются и их осколки будут разбросаны по разным орбитам. Они образуют замкнутые пояса наподобие колец Сатурна. Если поле пересекает не отдельное тело, а рой метеоритов или газо-пылевое облако то они, двигаясь с разными скоростями, оседают на разных орбитах, образуя множество кольцевых структур и изогнутых хвостов. То что все кольца вокруг планет лежат в одной плоскости, планеты вращаются в экваториальной плоскости Солнца, галактики имеют плоский линзаобразный вид, а большинство из них еще и спиральные рукава, не оставляет сомнений в том, что формирующей их силой является инерционное поле. Именно оно заставляет небесные тела вращаться, собираться в одной плоскости, иметь те конфигурации которые имеют. Гравитационное поле центрально-симметричное. Оно не может сферическое образование деформировать в плоское. Это может делать только инерционное поле. В системе мироздания оно играет роль архитектора в то время как гравитационное поле является ее строителем.

5. Некоторые вопросы космологии

Представим Метагалактику в виде плоского дискообразного скопления звезд с массой и радиусом, вращающейся с угловой скоростью в плоскости В качестве условного центра вращения выберем точку где находится наблюдатель. При вращении Метагалактика в этом центре создает инерционное поле с напряженностью

(5.1)

Учитывая, что , получим

(5.2)

гдесредняя плотность массы Метагалактики. Соотношение (5.2) хорошо подтверждается наблюдениями /7/. Подставляя из (5.2) в (2.3), получим

, (5.3)

Эта формула и внешне и численно совпадает с законом Хаблла. Но здесь означает не скорость расширения пространства, а скорость распространения грави-инерционных волн. Этим и объясняется и ее субсветовое значение. Полагая

, ,

находим радиус, массу, период обращения и другие параметры Метагалактики.

, ,

, (5.4)

Эти значения совпадают с данными ОТО, за исключением Т , который в ОТО характеризует не период обращения Метагалактики, а ее возраст. Определим радиус грави-инерционного взаимодействия потенциального поля Вселенной. Учитывая, что , из (1.20) имеем

, (5.5)

Выберем решение этого уравнения в виде

, (5.6)

тогда , (5.7)

где

Решение (5.7) зависит от знака . Для чисто грави-инерционного поля

, , (5.8)

Уравнение (5.7) с этим знаком имеет частное решение

, (5.9)

где - константы интегрирования. Обратная величинаопределяет радиус грави-инерционног