Практические задачи по ТОУЭС
1. Рассчитайте параметры сетевого графа
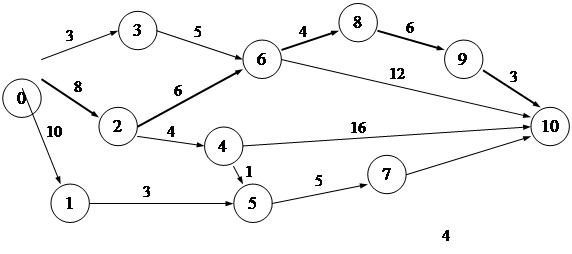
Работа i, j | Продол. | Ранние сроки | Поздние сроки | Полный резерв | Свободн. резерв | ||
tiPH | tjPO | tiПH | tjПО | ||||
| (0, 1) | 10 | 0 | 10 | 5 | 15 | 5 | 5 |
(0, 2) | 8 | 0 | 8 | 0 | 8 | 0К | 0 |
| (0, 3) | 3 | 0 | 3 | 6 | 9 | 0 | 0 |
| (1, 5) | 3 | 10 | 13 | 15 | 18 | 5 | 5 |
| (2, 4) | 4 | 8 | 12 | 9 | 13 | 1 | 1 |
(2, 6) | 6 | 8 | 14 | 8 | 14 | 0К | 0 |
| (3, 6) | 5 | 3 | 8 | 9 | 14 | 6 | 6 |
| (4, 5) | 1 | 12 | 13 | 17 | 18 | 5 | 5 |
| (4, 10) | 16 | 12 | 28 | 11 | 27 | -1 | -1 |
| (5, 7) | 5 | 13 | 18 | 18 | 23 | 5 | 5 |
(6, 8) | 4 | 14 | 18 | 14 | 18 | 0К | 0 |
| (6, 10) | 12 | 14 | 26 | 15 | 27 | 1 | 1 |
| (7, 10) | 4 | 18 | 22 | 23 | 27 | 5 | 5 |
(8, 9) | 6 | 18 | 24 | 18 | 24 | 0К | 0 |
(9, 10) | 3 | 24 | 27 | 24 | 27 | 0К | 0 |
К – критические операции
Продолжительность критического пути: 8 + 6 + 4 + 6 + 3 = 27
2. Оценить с достоверностью 90% оптимистичный
и пессимистичный срок завершения работ.
Эксперты | |||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 6 | 7 | 6 | 5 | 4 | 4 | 4 | 5 | 6 | 6 | 6 | 4 | 4 | 8 | 10 | 3 | 4 | 4 | 5 | 6 |
Упорядочиваем по возрастанию:
10, 8, 7, 6, 6, 6, 6, 6, 6, 5, 5, 5, 4, 4, 4, 4, 4, 4, 4, 3
Отбрасываем первые два значения и находим Qопт:
Qопт = 89 / 18 = 4,94
Упорядочиваем по убыванию и аналогично находим Qпес:
Qпес = 100 / 18 = 5,55
Находим Qср:
Qср = 107 / 20 = 5,35
Отклонение Qопт от Qср – 7,6%; Qпес от Qср – 3,7%. Оба значения в пределах 10%, таким образом достоверность 90% обеспечена.
3. Рассчитать требуемое количество экспертов, при котором влияние
1 эксперта на среднюю оценку составляет не более x = 9%.
Пробная оценка x + 1 экспертов:
6, 7, 6, 5, 4, 4, 4, 5, 6, 6
х = 9% => 0,91 £ E £ 1,09
Qср = 53 / 10 = 5,3
b = 10
T = ![]()
Таким образом, 9 человек – требуемое количество экспертов для проведения групповой оценки с влиянием одного эксперта не более 9%.
4. Проверить оптимальность указанных планов
f (x) = 3 x1 + 2 x2 – 4 x3 +5 x4 –> max
3 x1 + 2 x2 + 2 x3 – 2 x4 ³ -1
2 x1 + 2 x2 + 3 x3 – x4 ³ -1
x1 ³ 0 x2 ³ 0
x3 ³ 0 x4 ³ 0
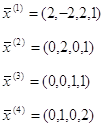
Координаты вектора x(1) не соответствуют ограничениям, т .к. х2 < 0
Остальные векторы подставляем в систему неравенств:
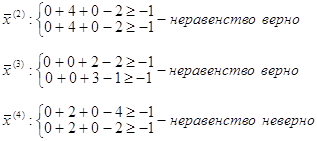
Таким образом, вектор х (4) тоже не удовлетворяет условиям. Вычисляем значения f(x):
x(2): f (x) = 0 + 4 – 0 + 5 = 9
x(3): f (x) = 0 + 0 - 4 + 5 = 1
Функция достигает максимума в x(2) (0, 2, 0, 1).
5. Решить графически задачу линейного программирования:
f (x) = 2 x1 + 4 x2 –> min
x1 + 2 x2 £ 5
3 x1 + x2 ³ 5
0 £ x1 £ 4 0 £ x2 £ 4
Найдем множество решений неравенств:
х1 + 2 х2 £ 5, если х1 = 0, то х2 £ 2,5
если х2 = 0, то х1 £ 5 точки прямой 1: (0; 2,5) и (5; 0)
3 х1 + х2 ³ 5, если х1 = 0, то х2 ³ 5
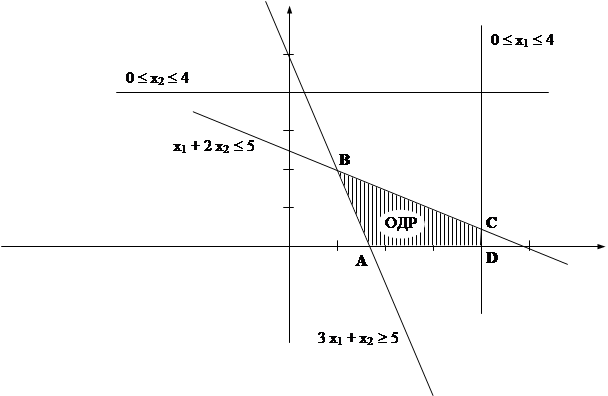 если х2 = 0, то х1 ³ 1, 67 точки прямой 2: (0; 5) и (1,67; 0)
если х2 = 0, то х1 ³ 1, 67 точки прямой 2: (0; 5) и (1,67; 0)
Найдем координаты точек A, B, C, D:
A (1,67; 0) и D (4; 0) – из неравенств
B (1; 2) как точка пересечения прямых из системы ![]()
С (4; 0,5) – x1 = 4 из неравенства x1<4, а x2 из уравнения 4 + 2 x2 = 5
Вычислим значение функции в этих точках:
A: f (x) = 2 * 1,67 + 4 * 0 = 3,33
B: f (x) = 2 * 1 + 4 * 2 = 10
C: f (x) = 2 * 4 + 4 * 0,5 = 10
D: f (x) =2 * 4 + 4 * 0 = 8
Функция принимает минимальное значение в точке A (1,67; 0).
6. Решить задачу
Механический завод при изготовлении 3-х разных деталей использует токарный, фрезерный и строгальный станки. при этом обработку каждой детали можно вести 2-мя разными способами. В таблице указаны ресурсы времени каждой группы станков, нормы времени при обработке детали на соответствующем станке по данному технологическому способу и прибыль от выпуска единицы детали каждого вида.
Норма времени, станко/час | Ресурсы времени | ||||||
Станок | I деталь | II деталь | III деталь | ||||
1 | 2 | 1 | 2 | 1 | 2 | ||
Токарный | 0,4 | 0,9 | 0,5 | 0,5 | 0,7 | – | 250 |
Фрезерный | 0,5 | – | 0,6 | 0,2 | 0,3 | 1,4 | 450 |
Строгальный | 0,3 | 0,5 | 0,4 | 1,5 | – | 1,0 | 600 |
Прибыль | 12 | 18 | 30 | ||||
Определить производственную программу, обеспечивающую максимальную прибыль.
Решение:
Пусть x1, x2, x3 – загрузка станков.
Таким образом 0 £ x1 £ 250;
0 £ x2 £ 450;
0 £ x3 £ 600.
При первом способе технологической обработки получаем:
0,4 x1 + 0,5 x2 + 0,7 x3 £ 250
0,5 x1 + 0,6 x2 + 0,3 x3 £ 450
0,3 x1 + 0,4 x2 £ 600
0,4 x1 + 0,5 x2 + 0,3 x3 ³ 12
0,5 x1 + 0,6 x2 + 0,4 x3 ³ 18
0,7 x1 + 0,3 x2 ³ 30
Необходимо найти решение, при котором f (x) = 12 x1 + 18 x2 + 30 x3 –> max