Прогнозирование макроэкономических переменных с помощью дублирующих портфелей
Государственный университет Высшая Школа Экономики
Курсовая работа
на тему:
«Прогнозирование макроэкономических переменных
с помощью дублирующих портфелей»
Выполнила Величко Оксана
группа 612
Москва 2003
СОДЕРЖАНИЕ
ВВЕДЕНИЕ......................................................................................................................................... 3
1 ПРОГНОЗИРОВАНИЕ В ЭКОНОМИКЕ.................................................................................... 4
1.1 Макроэкономические модели в прогнозировании................................................................ 4
1.2 Этапы экономико-математического моделирования............................................................ 5
1.3 Построение прогнозной модели.............................................................................................. 7
2 ДУБЛИРУЮЩИЕ ПОРТФЕЛИ................................................................................................... 12
2.1 Понятие дублирующего портфеля......................................................................................... 12
2.2 Простые дублирующие портфели......................................................................................... 13
2.3 Дублирующие портфели для непредвиденных изменений................................................ 14
3 ОБЗОР ПОДХОДОВ В ИССЛЕДОВАНИИ ДИНАМИКИ ДОХОДНОСТИ........................ 17
3.1 Использование текущих значений показателей.................................................................. 17
3.2 Использование будущих макроэкономических переменных............................................. 17
3.3 Применение векторной авторегрессии................................................................................. 18
4 ХАРАКТЕРИСТИКА И ОТБОР ФАКТОРОВ В МОДЕЛЬ...................................................... 19
4.1 Отбор факторов для построения дублирующего портфеля................................................ 19
4.2 Применение кластерного анализа......................................................................................... 23
5 ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ РАЗРАБОТКИ ПРОГНОЗА................................. 25
6 ПРОВЕРКА АДЕКВАТНОСТИ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ........................................ 26
ЗАКЛЮЧЕНИЕ................................................................................................................................. 28
СПИСОК ЛИТЕРАТУРЫ................................................................................................................ 29
ВВЕДЕНИЕ
В экономике основой практически любой деятельности является прогноз. Уже на основе прогноза составляется план действий и мероприятий. Таким образом, можно сказать, что прогноз макроэкономических переменных является основополагающей составляющей планов всех субъектов экономической деятельности.
Прогнозирование может осуществляться как на основе качественных (экспертных), так и с помощью количественных методов. Последние сами по себе могут ничего без качественного анализа, также как и экспертные оценки должны подкрепляться обоснованными расчетами.
В данной работе я сосредоточилась на одном из количественных методов прогнозирования – дублирующем портфеле. Само по себе построение такого портфеля не дает еще информации о будущем, но при построении дублирующего портфеля для будущих переменных позволяет выявить некую закономерность движения доходности активов и прогнозируемых макроэкономических переменных.
Дублирующий портфель – это портфель, доходность которого коррелирует с какой либо переменной. К примеру, такой портфель может дублировать экономическую переменную. Доходности за месяц акций и облигаций применяются для прогнозирования объема производства, валового дохода, инфляции, доходностей акций и облигаций. Эта прогнозирующая взаимосвязь проясняет идею портфелей, которые отражают ожидания рынка на счет будущих значения экономических переменных. Использование доходности дублирующих портфелей в качестве инструмента прогноза будущих значений экономических переменных существенно увеличивает оценочной чувствительность цен активов к новостям о значении в будущем данных переменных. Также данный вид портфелей используется при прогнозировании макроэкономических переменных и хеджировании экономического риска.
1 ПРОГНОЗИРОВАНИЕ В ЭКОНОМИКЕ
Прогнозирование – это способ научного предвидения, в котором используется как накопленный в прошлом опыт, так и текущие допущения насчет будущего с целью его определения. Основная функция прогноза – обоснование возможного состояния объекта в будущем или определение альтернативных путей. Выбор конкретного метода является одной из наиболее важных задач прогнозирования. Существует множество методов, позволяющих сделать прогноз, но необходимо выделить из их числа приемлемые для решения конкретной задачи.
В основе экономического прогнозирования лежит предположение о том, что будущее состояние экономики в значительной мере предопределяется ее прошлым и настоящим состояниями. Будущее несет в себе и элементы неопределенности. Это объясняется следующими моментами:
- наличием не одного, а множества вариантов возможного развития;
- действие экономических законов в будущем зависит не только от прошлого и настоящего состояний экономики, но и от управленческих решений, которые еще только должны быть приняты и реализованы;
- неполнота степени познания экономических законов, дефицит и недостаточная надежность информации.
Под методами прогнозирования следует понимать совокупность приемов и способов мышления, позволяющих на основе ретроспективных данных внешних и внутренних связей объекта прогнозирования, а также их измерений в рамках рассматриваемого явления или процесса вывести суждения определенного и достоверного относительно будущего состояния и развития объекта.
1.1 Макроэкономические модели в прогнозировании.
Экономико-математические модели в прогнозировании широко используются при составлении социально-экономических прогнозов на макроэкономическом уровне. К таким моделям относятся:
- однофакторные и многофакторные модели экономического роста;
- модели распределения общественного продукта (ВВП, ВНП, НД);
- структурные модели;
- межотраслевые модели;
- модели воспроизводства основных фондов;
- модели движения инвестиционных потоков и др.
При использовании этих моделей необходимо учитывать воздействие факторного, лагового и структурного аспектов сбалансированности экономики и их синтеза на основе принципа оптимальности.
Факторный аспект сбалансированности экономики основывается на взаимосвязи между объемом выпуска продукции и затратами факторов производства. Он сводится к определению такой пропорции между факторами производства, которая позволяет обеспечить заданный выпуск продукции. Для определения таких количественных пропорций используются показатели эффективности затрат живого и овеществленного труда и объемы этих затрат.
Лаговый аспект сбалансированности основан на распределении во времени затрат факторов производства и достигаемого при их взаимодействии эффекта. Главные лаговые характеристики связаны с воспроизводством основных фондов, а значит и с затратами капитальных вложений. Лаг – это запаздывание, временной интервал между двумя взаимозависимыми экономическими явлениями, одно из которых является причиной, а второе – следствием.
Структурный аспект сбалансированности основывается на пропорциях между I и II подразделениями общественного производства и взаимосвязях межотраслевых потоков продукции с элементами конечного потребления.
Условно все существующие методы прогнозирования можно разбить на две большие группы:
- фактографические, которые базируются на фактически имеющейся информации об объекте прогнозирования и его прошлом. Они условно подразделяются на статистические и аналоговые методы;
- экспертные методы используют мнения специалистов-экспертов и применяются тогда, когда невозможно формализовать изучаемые процессы или имеет место неопределенность развития хозяйственной системы.
1.2 Этапы экономико-математического моделирования
В различных отраслях знаний, в том числе и в экономике, этапы процесса моделирования приобретают свои специфические черты. Проанализируем последовательность и содержание этапов одного цикла построения:
1. Постановка экономической проблемы и ее качественный анализ. Главное здесь – четко сформулировать сущность проблемы, принимаемые допущения и те вопросы, на которые требуется получить ответы. Этот этап включает выделение важнейших черт и свойств моделируемого объекта и абстрагирование от второстепенных; изучение структуры объекта и основных зависимостей, связывающих его элементы; формулирование гипотез (хотя бы предварительных), объясняющих поведение и развитие объекта.
2. Построение математической модели. Это – этап формализации экономической проблемы, выражения ее в виде конкретных математических зависимостей и отношений. Обычно сначала определяется основная конструкция (тип) математической модели, а затем уточняются детали этой конструкции (конкретный перечень переменных и параметров, форма связей). Таким образом, построение модели подразделяется в свою очередь на несколько стадий.
Неправильно полагать, что чем больше фактов учитывает модель, тем она лучше "работает" и дает лучшие результаты. То же можно сказать о таких характеристиках сложности модели, как используемые формы математических зависимостей (линейные и нелинейные), учет факторов случайности и неопределенности и т.д.
Излишняя сложность и громоздкость модели затрудняют процесс исследования. Нужно учитывать не только реальные возможности информационного и математического обеспечения, но и сопоставлять затраты на моделирование с получаемым эффектом (при возрастании сложности модели прирост затрат может превысить прирост эффекта).
3. Математический анализ модели. Целью этого этапа является выяснение общих свойств модели. Здесь применяются чисто математические приемы исследования. Наиболее важный момент – доказательство существования решений в сформулированной модели. Если удастся доказать, что математическая задача не имеет решения, то необходимость в последующей работе по первоначальному варианту модели отпадает и следует скорректировать либо постановку экономической задачи, либо способы ее математической формализации.
4. Подготовка исходной информации. Моделирование предъявляет жесткие требования к системе информации. В то же время реальные возможности получения информации ограничивают выбор моделей, предназначаемых для практического использования. При этом принимается во внимание не только принципиальная возможность подготовки информации (за определенные сроки), но и затраты на подготовку соответствующих информационных массивов.
5. Численное решение. Этот этап включает разработку алгоритмов для численного решения задачи и непосредственное проведение расчетов. Трудности этого этапа обусловлены, прежде всего, большой размерностью экономических задач, необходимостью обработки значительных массивов информации.
6. Анализ результатов и их применение. На этом заключительном этапе цикла встает вопрос о правильности и полноте результатов, о степени практической применимости последних.
Математические методы проверки могут выявлять некорректные построения модели и тем самым сужать класс потенциально правильных моделей. Неформальный анализ теоретических выводов и численных результатов, получаемых посредством модели, сопоставление их с имеющимися знаниями и фактами действительности также позволяют обнаруживать недостатки постановки экономической задачи, сконструированной математической модели.
1.3 Построение прогнозной модели
Экономико-математическая модель это система формализованных соотношений, описывающих основные взаимосвязи элементов, образующих экономическую систему. Система экономико-математических моделей эконометрического типа служит для описания относительно сложных процессов экономического или социального характера.
Определенные виды моделей экономического и социального прогнозирования могут классифицироваться в зависимости от критерия оптимизации или наилучшего ожидаемого результата.
С учетом фактора времени модели могут быть статическими, когда ограничения в модели установлены для определенного отрезка времени, или динамическими – в этом случае ограничения установлены для нескольких отрезков времени.
Различают факторные и структурные модели экономического типа. Один и тот же тип моделей может быть применим к различным экономическим объектам. В зависимости от уровня рассмотрения показателей народного хозяйства различают макроэкономические, межотраслевые, отраслевые и региональные модели.
Факторные модели описывают зависимость уровня и динамики того или иного показателя от уровня и динамики влияющих на него экономических показателей – аргументов или факторов. Факторные модели могут включать различное количество переменных величин и соответствующих им параметров. Простейшими видами факторных моделей являются однофакторные, в которых фактором является какой-либо временный параметр. Многофакторные модели позволяют одновременно учитывать воздействие нескольких факторов на уровень и динамику прогнозируемого показателя.
Обоснованность прогноза в значительной мере зависит от выбора метода прогнозирования. Практическое применение того или иного метода прогнозирования определяется такими факторами, как объект прогноза, сложность и структура системы, наличие исходной информации, квалификация прогнозиста.
Экстраполяционные методы являются одним из самых распространенных и наиболее разработанных среди всей совокупности методов прогнозирования. В общем случае для экстраполяции необходимо иметь временной ряд, где каждому значению независимой переменной (в качестве которой выступает время) соответствует определенное значение прогнозируемою показателя. При формировании прогнозов с помощью экстраполяции обычно исходят из статистически складывающихся тенденций изменения тех или иных количественных характеристик объекта.
Следует отметить, что, поскольку метод разработан для анализа временных рядов, состоящих из большого числа наблюдений, а временные ряды в отраслевом прогнозировании, как правило, невелики, прогноз, сделанный с помощью этого метода, может не отразить некоторых существенных изменений.
Прогнозную экстраполяцию можно разбить на два этапа.
Выбор оптимального вида функции, описывающей ретроспективный ряд данных. Выбору математической функции для описания тренда предшествует преобразование исходных данных с использованием сглаживания и аналитического выравнивания динамического ряда. Расчет коэффициентов функции, выбранной для экстраполяции.
При разработке моделей прогнозирования тренд оказывается основной составляющей прогнозируемого временного ряда, на которую уже накладываются другие составляющие. Результат при этом связывается исключительно с ходом времени. Предполагается, что через время можно выразить влияние всех основных факторов. В статистической литературе под тенденцией развития понимают некоторое его общее направление, долговременную эволюцию. Обычно тенденцию стремятся представить в виде более или менее гладкой траектории.
Для оценки коэффициентов чаще остальных используется метод наименьших квадратов (МНК). Его сущность состоит в минимизации суммы квадратических отклонений между наблюдаемыми величинами и соответствующими оценками (расчетными величинами), вычисленными по подобранному уравнению связи.
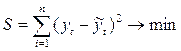 (1.1)
(1.1)
где ![]() – расчетные значения тренда;
– расчетные значения тренда;
y – фактические значения ретроспективного ряда;
– число наблюдений.
Этот метод лучше других соответствует идее усреднения как единичного влияния учтенных факторов, так и общего влияния неучтенных.
Операцию экстраполяции в общем виде можно представить в виде определения значения функции
![]() (1.2)
(1.2)
где ![]() - экстраполируемое значение уровня;
- экстраполируемое значение уровня;
L – период упреждения;
![]() - уровень, принятый за базу экстраполяции.
- уровень, принятый за базу экстраполяции.
Экстраполяция на основе средней.
В самом простом случае при предположении о том, что средний уровень ряда не имеет тенденции и к изменению или если это изменение незначительно, можно принять ![]() т. е. прогнозируемый уровень равен среднему значению уровней в прошлом. Доверительные границы для средней при небольшом числе наблюдений определяются следующим образом:
т. е. прогнозируемый уровень равен среднему значению уровней в прошлом. Доверительные границы для средней при небольшом числе наблюдений определяются следующим образом:
![]() (1.3)
(1.3)
где ta– табличное значение t-статистики Стьюдента с n-1 степенями свободы и уровнем вероятности ;
![]() – средняя квадратическая ошибка средней.
– средняя квадратическая ошибка средней.
Значение ее определяется по формуле ![]() . В свою очередь, среднее квадратическое отклонение S для выборки равно
. В свою очередь, среднее квадратическое отклонение S для выборки равно
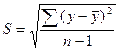 (1.4)
(1.4)
Доверительный интервал, полученный как ![]() , учитывает неопределенность, которая связана с оценкой средней величины. Общая дисперсия составит величину
, учитывает неопределенность, которая связана с оценкой средней величины. Общая дисперсия составит величину ![]() . Таким образом, доверительные интервалы для прогностической оценки равны
. Таким образом, доверительные интервалы для прогностической оценки равны
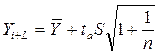 (1.5)
(1.5)
Недостаток рассмотренного подхода заключается в том, что доверительный интервал не связан с периодом упреждения.
Экстраполяция по скользящей и экспоненциальной средней.
Для краткосрочного прогнозирования наряду с другими приемами могут быть применены адаптивная или экспоненциальная скользящие средние. Если прогнозирование ведется на один шаг вперед, то ![]() или
или ![]() , где Мi - адаптивная скользящая средняя; Qi- экспоненциальная средняя. Здесь доверительный интервал для скользящей средней можно определить аналогично тому, как это было сделано в формуле (1.5), в которой число наблюдений обозначено символом n. Поскольку при расчете скользящей средней через m обозначалось число членов ряда, участвующих в расчете средней, то заменим в этой формуле n на m. Так как m обычно берется равной нечетным числам, то подсчитаем для них соответствующие значения величины
, где Мi - адаптивная скользящая средняя; Qi- экспоненциальная средняя. Здесь доверительный интервал для скользящей средней можно определить аналогично тому, как это было сделано в формуле (1.5), в которой число наблюдений обозначено символом n. Поскольку при расчете скользящей средней через m обозначалось число членов ряда, участвующих в расчете средней, то заменим в этой формуле n на m. Так как m обычно берется равной нечетным числам, то подсчитаем для них соответствующие значения величины ![]() . Что касается экспоненциального сглаживания, то, так как дисперсия экспоненциальной средней равна
. Что касается экспоненциального сглаживания, то, так как дисперсия экспоненциальной средней равна ![]() , где S2 - среднее квадратическое отклонение, вместо величины
, где S2 - среднее квадратическое отклонение, вместо величины ![]() в формуле, приведенной выше, при исчислении доверительного интервала прогноза следует взять величину
в формуле, приведенной выше, при исчислении доверительного интервала прогноза следует взять величину ![]() или
или ![]() . Здесь
. Здесь ![]() — коэффициент экспоненциального сглаживания.
— коэффициент экспоненциального сглаживания.
Корреляционный анализ используют для выявления и оценки связи между различными показателями. Степень тесноты связи оценивают коэффициентами, изменяющимися в пределах от 0 до 1, по следующей формуле:
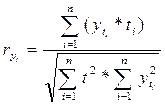 (1.6)
(1.6)
Малое значение коэффициента свидетельствует о слабой связи, значение, близкое к 1, характеризует очень сильную связь и часто позволяет предположить наличие функциональной причинно-следственной связи. Затем проверяют значимость коэффициента корреляции по критерию Стьюдента tj,k:
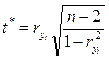 (1.7)
(1.7)
где k=n-2 – число степеней свободы.
При выполнении неравенства t*>yj,kгипотеза о не значимости коэффициента парной корреляции отвергается, т.е. yt зависит от фактора времени. Затем выбирают математическую модель взаимосвязи показателя от времени и рассчитывают критерии точности полученной модели.
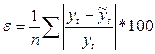 (1.8)
(1.8)
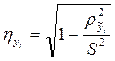 (1.9)
(1.9)
![]() (1.10)
(1.10)
где ![]() – средняя относительная ошибка;
– средняя относительная ошибка;
![]() – корреляционные отношения;
– корреляционные отношения;
S2 – остаточная дисперсия;
![]() – среднеквадратическое отклонение, рассчитанное по формуле:
– среднеквадратическое отклонение, рассчитанное по формуле:
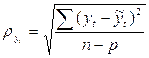 (1.11)
(1.11)
где - количество расчетных коэффициентов уравнения тренда.
Затем делают расчет точечной и интервальной оценки прогноза:
![]() (1.12)
(1.12)
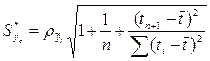 (1.13)
(1.13)
где yn+1 – прогнозируемая величина.
С помощью этих методов экстраполируются количественные параметры больших систем, количественные характеристики экономического, научного, производственного потенциала, данные о результативности научно-технического прогресса, характеристики соотношения отдельных подсистем, блоков, элементов в системе показателей сложных систем и др .
Анализ показывает, что ни один из существующих методов не может дать достаточной точности прогнозов на 20—25 лет. Применяемый в прогнозировании метод экстраполяции не дает точных результатов на длительный срок прогноза, потому что данный метод исходит из прошлого и настоящего, и тем самым погрешность накапливается. Этот метод дает положительные результаты на ближайшую перспективу прогнозирования тех или иных объектов — на 5—7 лет.
При экстраполяции часто используются линейные модели. Они требуют относительно небольшого количества вычислений и по тому, в частности, широко распространены в практике прогнозирования. Их недостаток, заключающийся в том, что лишь немногие явления в экономике могут быть адекватно описаны в линейном виде, отчасти преодолевается с помощью кусочно-линейной аппроксимации.
2 ДУБЛИРУЮЩИЕ ПОРТФЕЛИ
2.1 Понятие дублирующего портфеля
Изменение доходности активов, помимо прочих вещей, отражает изменения информации об экономических условиях в будущем. Изучение влияния различных экономических шоков на цены активов важно также и потому, что это помогает выявить природу экономических колебаний, оценить премию за риск и предсказать экономические колебания в будущем. Звеном, связывающим цены активов с новостями о состоянии экономики, является «дублирующий портфель» (tracking portfolio). Данный портфель представляет собой портфель активов, доходности которых максимально коррелированны с такими экономическими переменными как ожидаемые объем производства, инфляция или доходность.
В прикладных финансах давно сформировался подход связывать текущие доходности одного актива с доходностью других. Второй подход состоит в попытке объяснить поведение доходностей с помощью текущих или будущих экономических переменных. Портфель, дублирующий экономические переменные, сочетает в себе оба эти подхода. С одной стороны, экономический дублирующий портфель отражает доходность активов. С другой стороны, данный портфель получает доходность, которая имеет экономическую интерпретацию. Формирование портфеля, дублирующего экономические переменные, является способом использования текущей доходности активов в качестве инструментов для измерения будущих переменных.
Дублирующие портфели применяются при решении нескольких вопросов. Одной из проблем является измерение премии за риск. Если дублирующий портфель приносит премию за риск, то тогда знак этой премии и тождество премии, сгенерированной экономическим параметром, могут указать на то, какие экономические параметры значимо влияют на ожидаемую доходность, и могут помочь оценить модель оценки финансовых активов.
Дублирующие портфели имеют как минимум еще три сферы применения, которые не основываются на портфелях, приносящих ненулевую премию за риск. Во-первых, эти портфели могут служить средством хеджирования для индивидуальных инвесторов, которые желают застраховать себя на случай какого-либо определенного экономического риска (например, снижение потребления). Во-вторых, на основе дублирующего портфеля можно строить прогноз поведения какой-либо экономической переменной. Т.к. доходности активов могут быть рассчитаны на каждый день, дублирующие портфели могут предоставить информацию по поводу ожиданий рынка на счет будущего экономики. В-третьих, путем измерения ожиданий, портфели следования выявляют структуру экономики и объясняют реакцию цен на новости, касающиеся экономической сферы.
Эти три сферы приложения дублирующих портфелей могут быть проверены на практике и не зависят от конкретной модели оценки активов. Например, если предположить, что CAPM-модель верна, то в этом случае дублирующий портфель имел бы ожидаемую доходность, имеющую тесную ковариацию с рынком. Но тогда неожидаемая часть доходности была бы все равно отражением новостей о будущем состоянии экономики. Напротив, если предположить, что рынок неэффективен, иррациональные настроения влияют на цены, и доходность частично предсказуема, то в этом случае до тех пор пока цены отражают информацию о будущем состоянии экономических детерминант, доходность дублирующего портфеля также будет применима для хеджирования, прогнозировании и понимания экономики.
2.2 Простые дублирующие портфели
Дублирующий портфель для любой переменной у может быть определен как регрессия у на доходности некоторого набора базовых активов. Доли активов, входящих в дублирующий портфель для у, идентичны коэффициентам в регрессии, построенной с помощью метода наименьших квадратов. Если у является переменной, влияющей на ценообразование базового актива, тогда мультифакторная модель выполняется с одним фактором, который отслеживает портфель, дублирующий переменную у. Однако, даже если у не является значимой переменной для ценообразования активов, то портфель, дублирующий эту переменную, также остается интересным объектом с экономической точки зрения, т.к. он отражает изменения рыночных ожиданий относительной у.
Следующие три утверждения эквивалентны определения дублирующего портфеля. Среди всех возможных линейных комбинаций доходностей базовых активов дублирующий портфель имеет:
А) минимальную вариацию среди всех портфелей с заданной бетой (коэффициентом регрессии) в регрессии доходности портфеля на у;
Б) доходность, максимально возможно коррелирующую с у;
В) наибольший R2 в регрессии у на доходность активов.
Эквивалентность данных трех утверждений может быть доказана и с помощью матричной алгебры, и с помощью более простых выкладок. Обозначим:
r – доходность портфеля базовых активов, r = bR,
– вектор весов активов в портфеле,
R – вектор доходностей данных активов.
Дублирующим портфелем является портфель с весами, которые минимизируют вариацию данного портфеля на у. Другими словами, подбирается таким образом, чтобы минимизировать ![]() при заданной
при заданной ![]() (где
(где 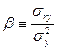 - коэффициент регрессии r на у). Т.к.
- коэффициент регрессии r на у). Т.к. ![]() , минимизация
, минимизация ![]() эквивалентна минимизации
эквивалентна минимизации 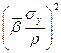 , что эквивалентно максимизации
, что эквивалентно максимизации ![]() (где ρ – коэффициент корреляции между у и r). Т.к. R2 в простой регрессии является
(где ρ – коэффициент корреляции между у и r). Т.к. R2 в простой регрессии является ![]() и т.к. метод наименьших квадратов максимизирует R2 , решение данной задачи максимизации идентично уравнению регрессии, построенному с помощью МНК.
и т.к. метод наименьших квадратов максимизирует R2 , решение данной задачи максимизации идентично уравнению регрессии, построенному с помощью МНК.
2.3 Дублирующие портфели для непредвиденных изменений
На основе данной теории можно сформировать портфель с непредвиденными доходностями, которыми максимально коррелируют с непредвиденным компонентом будущего значения переменной у. Таким образом, основной переменной являются «новости» о yt+k, где yt+k – макроэкономическая переменная, например темп инфляции в период t+k. Новости являются чем-то новым в ожиданиях относительно yt+k , причем ![]() . Например,
. Например, ![]() может представлять собой новости, о которых уведомлен рынок в июле 2002 года о темпе инфляции между июлем 2002 и июлем 2003 года.
может представлять собой новости, о которых уведомлен рынок в июле 2002 года о темпе инфляции между июлем 2002 и июлем 2003 года.
![]() – доходность дублирующего портфеля, где
– доходность дублирующего портфеля, где ![]() и
и ![]() – доходности с конца периода t-1 до конца периода t. Дублирующий портфель формируется на основе непредвиденных доходностей базовых активов. Непредвиденная доходность – это действительная доходность за вычетом ожидаемой доходности с учетом того, что
– доходности с конца периода t-1 до конца периода t. Дублирующий портфель формируется на основе непредвиденных доходностей базовых активов. Непредвиденная доходность – это действительная доходность за вычетом ожидаемой доходности с учетом того, что ![]() . Веса в портфеле выбираются таким образом, что
. Веса в портфеле выбираются таким образом, что ![]() максимально коррелирует с
максимально коррелирует с ![]() .
.
Оценивание дублирующих новости портфелей является немного более сложным процессом, чем оценивание простых дублирующих портфелей. Всегда можно написать проектное уравнение новостей на неожиданную составляющую доходности. Ключевым предположением является то, что изменения в доходностях отражают изменения в ожиданиях относительно значений переменных в будущем, т.е. ненулевое решение в уравнении:
![]() , (2.1)
, (2.1)
где ht – составляющая новостей, ортогональная неожиданному компоненту доходности.
Т.к. неожиданная составляющая доходности активов отражает новости по поводу будущего денежного потока и дисконтных ставок, вектор а будет ненулевым для любой переменной, коррелированной с будущими денежными потоками и дисконтными ставками.
Из уравнения (2.1) может показаться, что необходимо определить ![]() для того, чтобы построить регрессию. К счастью, этого можно избежать, и все, что необходимо для оценивания регрессии, – это
для того, чтобы построить регрессию. К счастью, этого можно избежать, и все, что необходимо для оценивания регрессии, – это ![]() (непредвиденный компонент доходности в период t).
(непредвиденный компонент доходности в период t).
Реализация переменной yt+k может быть переписана как сумма ожиданий в период t-1, непредвиденных изменений в ожиданиях в период t и с периода t до t+k.
![]() (2.2)
(2.2)
Здесь следует сделать второе предположение о том, что ожидаемые доходности базовых активов в период t являются линейной функцией от Zt-1– вектора контрольных переменных, значения которых известны в период t-1:
![]() (2.3)
(2.3)
Т.к. предположение, содержащиеся в уравнении (2.3) является потенциальной причиной ошибки спецификации модели, можно ожидать, что эмпирические результаты применения данной ошибочной модели будут относительно грубы, т.к. доходности активов достаточно непредсказуемы на коротком горизонте прогнозирования.
Таким образом, для дальнейшего удобства определим проектное уравнение лагированных ожиданий у как лагирование контролируемые переменных:
![]() (2.4)
(2.4)
Объединяя уравнения (2.1) – (2.4), получаем:
![]()
![]()
![]()
![]()
![]() (2.5)
(2.5)
где b = a, c = f – ad и ![]() .
.
Уравнение (2.5) является уравнением регрессии с будущим значением у в левой части и доходностью в период t и значением контрольных переменных в период t-1 в правой. Это уравнение состоятельно, т.к. все три составляющие ![]() по определению ортогональны как
по определению ортогональны как ![]() , так и
, так и ![]() .
.
МНК-регрессия, обозначенная уравнением (2.5), приводит к ![]() – портфелю, непредвиденный компонент которого максимально коррелирует с
– портфелю, непредвиденный компонент которого максимально коррелирует с ![]() . . В диссертации я предполагаю оценивать уравнение (2.5) и объяснить свойства получившихся дублирующих портфелей. Уравнение (2.5) практически не имеет теоретического смысла и зависит только от предположения, что изменения в ожиданиях на счет будущего значения у находят отражение в доходности активов, и то, что ожидаемая доходность активов является функцией лагированных контрольных переменных.
. . В диссертации я предполагаю оценивать уравнение (2.5) и объяснить свойства получившихся дублирующих портфелей. Уравнение (2.5) практически не имеет теоретического смысла и зависит только от предположения, что изменения в ожиданиях на счет будущего значения у находят отражение в доходности активов, и то, что ожидаемая доходность активов является функцией лагированных контрольных переменных.
Здесь можно сделать несколько комментариев на счет практического применения уравнения (2.5). Во-первых, предполагается использование доходности портфеля с нулевыми издержками ![]() . Использование портфеля с нулевыми издержками означает, что нет необходимости накладывать ограничения на веса портфеля. Конечный дублирующий портфель является незатратным, т.к. является линейной комбинацией портфелей с нулевыми издержками.
. Использование портфеля с нулевыми издержками означает, что нет необходимости накладывать ограничения на веса портфеля. Конечный дублирующий портфель является незатратным, т.к. является линейной комбинацией портфелей с нулевыми издержками.
Во-вторых, предполагается использовать в качестве базы доходности активов за месяц. Используя более длинные горизонты для базовых активов (к примеру, годовые доходности) следует быть более осторожным, т.к. с увеличением интервала повышается предсказуемость доходностей и оценки регрессии могут стать более чувствительными к отклонению от уравнения (2.3).
В-третьих, может показаться, что следует отобраться только такие базовые активы, доходности которых является наиболее информативными в плане объяснения ожиданий будущего значения у. Но в данном случае важным моментом является то, что различные активы имеют разные чувствительности к будущему значению у. Таким образом, регрессия должна являться линейной комбинацией доходностей активов, которые хеджируют общую составляющую вариации доходности, которая некоррелирована с будущим значением у.
В-четвертых, главной причиной выбора контролируемых переменных должна являться модель ожидаемой доходности, т.е. ![]() должна включать переменные, которые прогнозируют доходность базовых активов. Если же доходности активов полностью непредсказуемы, или если
должна включать переменные, которые прогнозируют доходность базовых активов. Если же доходности активов полностью непредсказуемы, или если ![]() некоррелирована с
некоррелирована с ![]() , не следует включать вообще никаких контролируемых переменных. Вспомогательной ролью лагированной контролируемой переменной в уравнении (2.5) является помощь в объяснении будущего значения у. Включая в
, не следует включать вообще никаких контролируемых переменных. Вспомогательной ролью лагированной контролируемой переменной в уравнении (2.5) является помощь в объяснении будущего значения у. Включая в ![]() переменные, коррелирующие с
переменные, коррелирующие с ![]() , можно уменьшить вариацию остатков в уравнении (2.5) и, таким образом, более точно оценить параметр .
, можно уменьшить вариацию остатков в уравнении (2.5) и, таким образом, более точно оценить параметр .
В-пятых, добавление переменных в ![]() и
и ![]() сопряжено с издержками, т.к. чем больше переменных включается, тем более остро встает проблема практического объяснения и ложных выводов.
сопряжено с издержками, т.к. чем больше переменных включается, тем более остро встает проблема практического объяснения и ложных выводов.
Одним из применений дублирующих портфелей является хеджирование экономического риска существующих активов. Альтернативный подход – это создание абсолютно новых активов, соотносящихся с экономическими переменными. Экономические дублирующие портфели, использующие существующие ликвидные активы, облегчают данную задачу, т.к. дублирующие портфели помогают эмитентам новых ценных бумаг частично хеджировать себя от экономического риска.
Другим практическим применением экономических дублирующих портфелей является анализ взаимосвязи экономических переменных и цен активов. Исследования этого вопроса в экономике проходили по трем направлениям: с использованием текущих экономических параметров, с использованием будущих значений данных параметров и с использованием и тех и других в векторной авторегрессии.
3.1 Использование текущих значений показателей
Первый подход включает в себя доходности активов современные значения экономических параметров. Примером данного подхода является работа Chen, Roll and Ross (1986), в которой делается вывод, что ковариация с ростом промышленного производства, инфляции и доходности облигаций приводит к премии за риск.
К сожалению, попытки составить факторный портфель (factor mimicking portfolio) для макроэкономических показателей не увенчались успехом. Chan, Karceski и Lakonishok (1998) сконструировали портфели путем сортировки ценных бумаг по месячной текущей корреляции за пятилетний период. Они сформировали портфели, основанные на инфляции и промышленном производстве. После изучения доходности портфелей был сделан вывод, что макроэ