Цифровая обработка сигнала (Digital Signal processing)
Устройства, которые позволяют вводить сигналы в ЭВМ, называются АЦП.
Любой сигнал содержит шумы, которые искажают последний сигнал, тем самым, мешая обработке сигнала.
Метод обработки сигналов.
Существует 3 способа обработки сигналов:
1 способ – полосовые фильтры.
2 способ – линейные предсказания.
3 способ – дискретное преобразование Фурье.
Применение методов обработки сигналов.
1) Выделение наиболее информативных признаков из имеющегося сигнала.
2) Создание векадерной техники.
3) Создание речевых систем для автоматической распознавания речи.
4) Проблема синтеза речи или создание искусственного голоса.
5)
Системы распознавания речи.
Классификация:
Это такие устройства, которые позволяют отредактировать устный сигнал в команды
Классы систем:
1) автоматическое распознавание изолированных слов (когда пользователь пословно производит команды).
2) Автоматическое распознавание слитной речи (устройства, которые в состоянии отделить слова).
3) Система понимания речи (системы, которые не требуют отделять слова, а которые должны их понимать и дополнять).
4) Системы синтеза речи или сигналы создания искусственного голоса.
А) форматный синтез или синтез по правилам (когда выходной сигнал получается при сложной математической обработки).
Б) компилятивный метод (этот метод: суть: предварительное изучение и выделение ярких моментов).
Параметры распознавания систем:
1. По объему словаря.
2. Оценить по точности распознавания речи, которая измеряется в процентах (должно превышать 95%).
3. Система автоматического распознавания речи характеризуется по способу обработки входного сообщения.
4. Система распознавания диктора.
Основные информативные признаки речевого сигнала.
Любой речевой сигнал характеризуется следующими признаками, которые можно использовать для того, чтобы синтезировать исходный сигнал.
Признаки:
1) Энергия сигнала
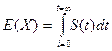

![]()
![]()
![]()
10м
Е1 Е2 Е3
![]()
N – количество отчетов
2) Основная частота.
![]() - определяет длину речевого тракта
- определяет длину речевого тракта
3) Форманты
![]()
Е

![]()
![]()
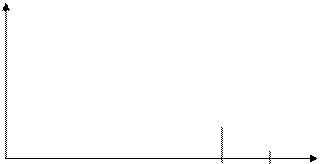
F0 F1 F2 F3 F4
![]() - определяет концентрацию энергии речевого сигнала по частоте и характеризует гласные звуки. Они используются для классификации гласных звуков.
- определяет концентрацию энергии речевого сигнала по частоте и характеризует гласные звуки. Они используются для классификации гласных звуков.
![]() - характеризует свойства диктора.
- характеризует свойства диктора.
4) Мгновенная частота.
Это количество перехода сигнала через нуль.
![]()
Этот признак используется для классификации шумных звуков и гласных.
5) Мгновенная амплитуда сигнала.
![]()
Аналогичные признаки выделяются из речевого сигнала после его фильтрования по полосовым фильтрам. В результате получается компактные речевые признаки входного сигнала. Объем памяти получается необходимым намного меньше. Основной тон ![]() - это очень полезный признак и используется для динамической сегментации входного сигнала, который приводит к более точной обработке входного сигнала.
- это очень полезный признак и используется для динамической сегментации входного сигнала, который приводит к более точной обработке входного сигнала.
Первая и вторая форманта ![]() - используются для классификации и распознавания гласных звуков.
- используются для классификации и распознавания гласных звуков.
Признак ![]() - используется для определения взрывных звуков (т, с, ш и т.д.)
- используется для определения взрывных звуков (т, с, ш и т.д.)
Структура распознавания входных сообщений.
Модель сигнала Гипотеза фонем Предсказатель букв Предсказатель слов


Предсказатель предложений, фраз
![]()
![]() Методы распознавания, используемые в системах обработки речевых сигналов.
Методы распознавания, используемые в системах обработки речевых сигналов.
1) Статистические методы.
2) Лингвистические методы (структурирование).
3) Нейронные сети.
Тема: Типы сигналов и связи между сигналами различных типов.
1) Классификация сигналов.
2) Связи между аналоговыми и дискретными сигналами.
3) Связь между дискретными и цифровыми сигналами.
4) Дискретная Дельта – Функция.
![]()
m=3 – номер отсчета
![]()
![]()
![]()
![]()
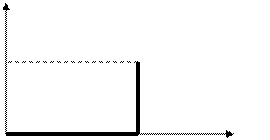

T 2T 3T
Используя дискретную ![]() - функцию, любую последовательность X(nT) можно представить в следующей форме:
- функцию, любую последовательность X(nT) можно представить в следующей форме:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Тема: Z–преобразования и преобразования Фурье.
1) Прямое Z–преобразование.
2) Основные свойства прямого Z–преобразования.
3) Обратное Z–преобразование.
4) Преобразование Фурье.
1. Прямое Z–преобразование X(Z) последовательность X(nT) определяется следующей формулой:
![]()
![]()
Z–преобразование имеет смысл только в том случае, если функция X(nT) сходится.
Пример:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
В теории обработки цифровых сигналов могут быть использованы:
|
|
1 (-1)n | 1/(1-Z-1) 1/(1+Z-1) Z-1/(1-Z-1)2 |
![]()
![]()
Вот эти Z–преобразования имеют различные формы записи и могут использоваться для описания передаточных функций цифровых фильтров, которые используются для обработки цифровых сигналов.
![]()
![]() X(nT) X(Z)
X(nT) X(Z) ![]()
![]()
Z–преобразование используют для того, чтобы проектировать цифровые фильтры.
2. Основные свойства прямого Z–преобразование.
1. Свойство линейности.
Предположим, имеем следующую последовательность дискретного преобразования:
X1(nT) X2(nT) X3(nT)
X1(Z) X2(Z) X3(Z)
Имеем: С1=const и C2=const, тогда преобразование является линейным если:
X3(Z) = C1X1 (Z) +C2X2 (Z) - линейное
X3(nT) = C1X1(nT) +C2X2(nT) преобразование
2. Свойства сдвига.
Утверждает, что если
X2(nT) = X1((n-m)T), тогда
X2(Z) = X1(-mT)+ X1((-m+1)T)Z-1+…+X1(-T)Z-(m-1)+Z-mX1(Z)
X2(Z) = Z-mX1(Z)
X3(Z) = ![]()
Где с – замкнутый контур в комплексной v плоскости, которая обхватывает все особенности X1 u X2 .
3. Обратное Z–преобразование.
Оно определяется следующей функцией:
![]()
Обратное Z–преобразование может быть определено путем вычисления интеграла, который можно записать следующим образом:
![]()
![]()
Обратное Z–преобразование может быть определено путем вычисления интеграла, если этот интеграл не расходится.
Z–преобразование используется при проектировании фильтров и характеристик спектральных.
Тема: MatLab – основные возможности и функции по дискретной обработке сигналов.
MatLab – пакет прикладных программ по основным функциям обработки.
Задачи:
- Можно проектировать фильтры.
- Выполнять частотный и спектральный анализ сигналов.
- Выделение признаков из дискретного сигнала и моделирование параметров.
· Фильтрация
Пакет позволяет выполнять фильтрацию сигнала а с помощью следующих типов фильтра:
а) Низкочастотные.
б) Полосовые.
в) Высокочастотные.
· Этот пакет позволяет выплнять спектральный анализ, ДПФ(дискретное преобразование Фурье), выполнять непрерывные преобразования Фурье, можно выполнять Z–преобразования сигнала. В интервальном режиме можно проектировать сигналы определенной формы. Можно моделировать сигнал.
· Основные свойства прямого Z–преобразования.
1. Свойство линейности.
X1(nT) X2(nT) X3(nT) с1,с2
X1(Z) X2(Z) X3(Z)
2. Сдвиг.
· Другой метод обработки сигналов это метод преобразования ряда Фурье.
X(nT) – показывает комплексную функцию Х(еj), которая выглядит:
![]() - прямое преобразование.
- прямое преобразование.
![]()
Спектр сигнала можно получить с помощью Z–преобразования если подставить:
![]()
Из свойства линейности Z–преобразования следует свойство линейности Фурье преобразования.
![]() , то
, то
![]()
Из свойства сдвига, мы можем написать следующим образом:
![]()
![]()
· Дискретное преобразование Фурье.
![]() K= 0, … N-1 – прямое
K= 0, … N-1 – прямое
![]() n= 0, … N-1 – обратное
n= 0, … N-1 – обратное
X(nT) = (n=0, … N-1)
X(K)последовательность из N частотных отсчетов, где
![]()
Эти преобразования можно представить в матричной форме:
X = WnX
![]()
![]()
![]()
![]()
![]() Wn – окно расчета
Wn – окно расчета
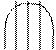
![]()
![]() - окно Хэминга
- окно Хэминга
![]() N
N
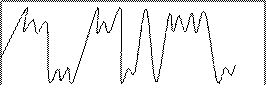
ДПФ и ОПФ – выполняются над конечной последовательностью из N – отсчетов и этот вид преобразования дает возможность определить спектральную плотность мощности сигнала, амплитуду и фазу отдельных частот.
![]()
![]() S1 S1 = a1sin(wt)
S1 S1 = a1sin(wt)
![]()
![]()
![]()
![]()
![]()
![]()
S2 S2 = a2sin (w2t)
![]() S3 S3 = a3sin (w3t)
S3 S3 = a3sin (w3t)
![]()
![]()
Спектральная плотность сигнала
Е

 w
w
F1 u F2 –несет смысл сообщения
F3 и т.д. – несет источник информации.
Свойства дискретного преобразования Фурье.
1) Линейность.
Имеются 2 сигнала х(к) у(к)
aх(nT) by(nT) тогда получается
ax(k)+by(k)=ax(nT)+by(nT)
2) Свойство сдвига.
Х(к) X(nT) – путем сдвига на n0 отсчетов, тогда дискретное
Y(nT) преобразование Фурье будет:
![]() путем сдвига на n0k.
путем сдвига на n0k.
![]()
![]()
![]()

![]()
![]()
![]()
![]() nT
nT
![]()
![]() X(nT)
X(nT)

![]()
![]()
![]()
![]() nT
nT
Тема: Случайные последовательности и их характеристики.
Любой сигнал который подвергается обработке в какой-то степени является случайным сигналом, который изменяется по времени и по частоте. Последовательность X(nT) является случайной, если каждый ее элемент является случайной величиной.
![]() - помеха
- помеха
X(nT)
 Y(nT)
Y(nT) ![]()
Характеристики:
1) Математическое ожидание.
![]()
![]()
Х(nТ)
![]()
![]()
N-1 N
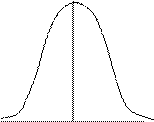
2) Дисперсия.
Дисперсия сигнала для непрерывной случайной величины определяется так:
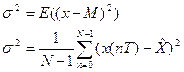
![]()
![]()
![]() 0
0 ![]()
95%
3) Авто корреляция.
Корреляция – связь между нынешним и предыдущим состоянием.
![]()
![]() - среднее значение или математическое ожидание.
- среднее значение или математическое ожидание.
![]()
![]()
Авто корреляционная функция является мерой связей между случайными последовательностями. Если значение r(m)=0, то нет никакой связи межу случайными последовательностями.
4) Спектральная плотность или мощность стационарной случайной последовательности.
Спектральная плотность сигнала ----- есть средняя мощность последовательности ----- , приходящейся на достаточно узкую полосу частот.
Эта функция связана с преобразованием Фурье, и имеет следующий вид:
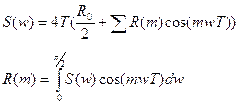
Тема: Виды окон анализа.
Проблемы:
1) Для того, чтобы обрабатывать сигнал в начале он превращается в дискретном виде (необходимо решить проблему точности при вставлении сигнала, как по частям, так и по уровню).
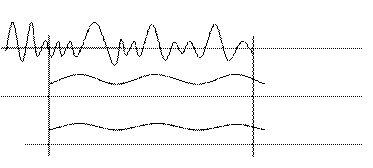
2) Выбор ширины окна анализа сигнала и типа окна анализа. Ширина окна берется исходя из периодичности сигнала. Если ширина окна близка или в точности совпадает с периодичностью сигнала, то это наиболее оптимальный способ выбора ширины окна.
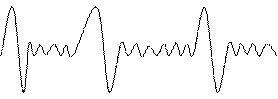 Для речевых сигналов ширина окна должна быть равна периоду основного тона сигнала.
Для речевых сигналов ширина окна должна быть равна периоду основного тона сигнала.

Т0
Тип окна - используются несколько типов:
а) прямоугольное окно.

Частотная характеристика этого окна выглядит так:
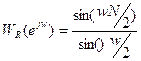
![]()
![]()


б) Окно Хэмминга.
Окно Хэмминга отличается от прямоугольного окна и описывается следующей формулой:
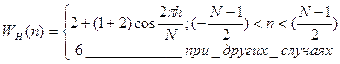
Достоинства:
1) Она сглаживает боковые вклады в результат обработки.
2) Ширина сдвига окна меньше ширины всего окна.
в) Окно Кайзера.
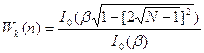 , где
, где
I0 – функция Бегеля
![]() - const
- const
Тема: Расчеты цифровых фильтров.
Случайные сигналы можно исследовать:
2. В области частот.
Этот способ позволяет найти компоненты периодических сигналов, которые формируют или образуют случайные сигналы.
а) Преобразованием Фурье.
Сигналы можно разделить на 3 гармоники.
б) С помощью полосовых фильтров.


2. Во временной области.
Исследование его характеристики во времени.

3. С помощью линейного предсказания.
Это авто корреляционный способ. Он использует закономерность или информацию о том, как соседние отсчеты взаимосвязаны между собой.
Для того, чтобы исследовать сигналы в частотной области с помощью программ, которые моделируют цифровые фильтры, необходимо, заранее делать расчет цифровых фильтров.
Порядок расчета цифровых фильтров следующий:
1) Решается задача аппроксимации с целью определения коэффициента фильтра, при котором фильтр удовлетворяет заданному требованию.
2) Выбирается конкретная схема построения фильтра и квантования, найденных значений его коэффициентов в соответствии с фиксированной длиной слова.
3) Делается квантование переменных величин фильтра, т.е. выбор длины слова входных выходных и промежуточных переменных.
4) Проверяется методом моделирования, удовлетворяет ли полученный фильтр заданным требованиям. Если на этом этапе фильтр не удовлетворяет заданным требованиям, то предыдущие 2 и 3 этапы повторяются.
Бывают 2 типа фильтров:
а) Нерекуррентные.
б) Рекуррентные.
Формулы определения фильтров.
![]() - рекуррентный фильтр
- рекуррентный фильтр
Другую характеристику цифрового фильтра можно записать следующим образом:
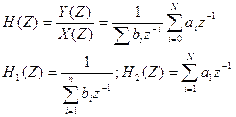
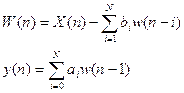
Схема фильтра будет следующая:
X(n) W(n) a0 Y(n)
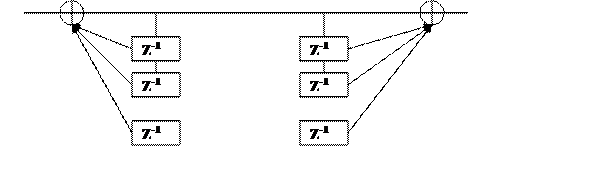

Схема фильтра состоит из набора элементов задержек, выходной сигнал которых
умножается на определенный коэффициент.
Тема: Линейное предсказание сигналов.
Один из способов обработки сигналов является: использование модели линейного предсказания. Суть состоит в том, что следующий отчет сигнала является (вычисляется), используя предыдущие отчеты.
---- реальный дискретный сигнал.
---- моделирование дискретных сигналов.
С другой стороны:
![]() - модель сигнала
- модель сигнала
![]()
Ошибка ![]()
![]()
![]()
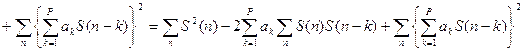
Минимизируем функцию.
![]()
![]()
![]()
![]()
ak – коэффициент линейного предсказания.
![]()

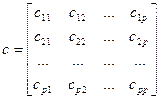
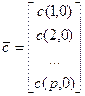
Решая эту систему, находим коэффициент а
![]()
- Это Ковариационный метод.
![]()
- Авто корреляционный метод.
Модель такая: минимизируется ошибка следующим образом:
![]()
а – коэффициент линейного предсказания.
R – авто корреляционная матрица.
r – коэффициенты матрицы.
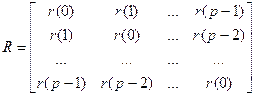
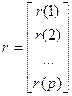
Эта модель сводится к модели фильтрации сигналов и будет:
![]()
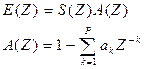
S(Z) - Z–преобразование сигнала
A(Z) – фильтр (анализатор) сигнала
Любая модель линейного предсказания приводит к ошибкам предсказания. В случае, если мы используем авто корреляционный метод, тогда ошибка предсказания будет:
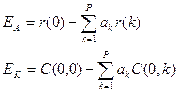
Тема: Цифровая обработка сигналов.
1) Достоинства методов цифровой обработки сигналов.
2) Линейные и дискретные системы и их свойства.
3) Цифровые фильтры и способы их описания.
4) Фильтры с конечно импульсными характеристиками.
5) Фильтры с бесконечно импульсными характеристиками.
6) Передаточные характеристики фильтров.
7) Нули и полюса фильтров.
8) Фильтры первого порядка с одним нулем и с одним полюсом.
9) Фильтры второго порядка с нулями и плюсами.
10) Топология фильтров.
I. Достоинства ЦОС.
- Экономное использование средств для обработки сигналов.
- Гибко использовать программные средства для обработки сигналов различными методами.
- Цифровые способы обработки сигналов не зависят от внешних условий.
- Цифровые способы позволяют моделировать любые устройства с необходимыми характеристиками.
II. Цифровая обработка сигналов использует линейные дискретные системы, которые наиболее проще описывают те процессы, которые протекают при обработке сигналов.
Свойства:
1. Однородности:
![]()
![]()
|